Opis i cel ćwiczenia

Do wykonania zadania laboratoryjego użyjemy przypadków rozpraszania proton-proton przy energii 7 TeV (LHC - Large Hadron Collider LHC Website). Procesy fizyczne, które zachodzą podczas zderzania protonów modelowane są przy pomocy generatora fizycznego PYTHIA8 (PYTHIA Web Page). Wynikiem 'wygenerowania' przypadku jest lista cząstek wyprodukowanych w wierzchołku pierwotnym (czyli w miejscu gdzie zaszło oddziaływanie proton-proton) oraz ich czteropędy. Cząstki te nazywamy cząstkami pierwotnymi (ang. prompt particles). W większości są to obiekty niestabilne, które posiadają bardzo zróżnicowane czasy życia od 10^-23 s (rezonansy hadronowe) do 10² s. Cząstki, które powstały na skutek rozpadu cząstek pierwotnych nazywamy wtórnymi (ang. secondary). W jednym przypadku obserwujemy od kilkudziesięciu do kilkuset cząstek, które docierają do aparatury detekcyjnej. Przykład 'typowego' przypadku (dane nie symulacja) pokazany jest poniżej.


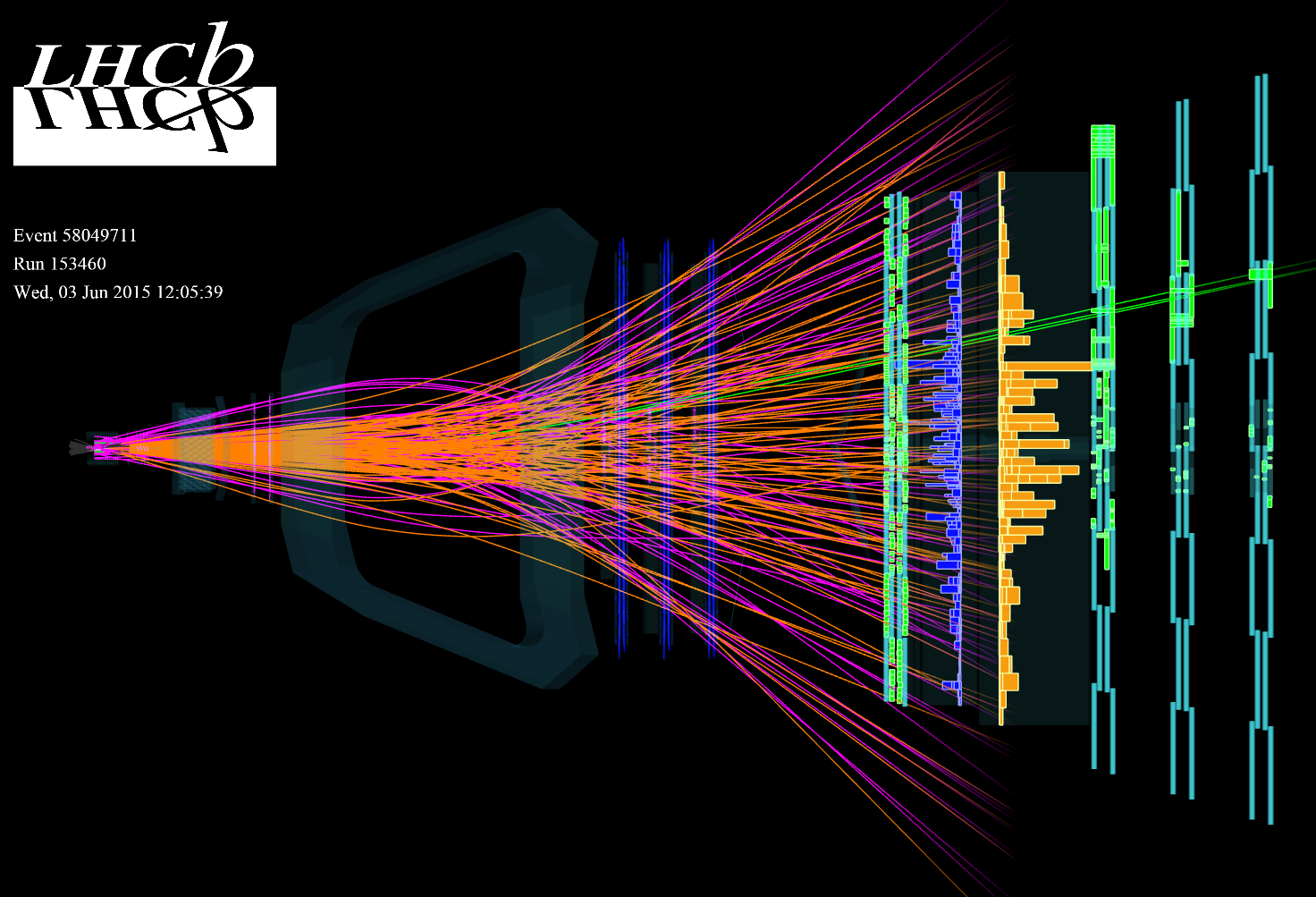
Rysunek 1. Przykład typowego przypadku oddziaływania proton-proton przy energii LHC. Linie reprezentują zrekonstruowane trajektorie cząstek powstałych w oddziaływaniu.

Detektor LHCb (Large Hadron Collider beauty experiment LHCb Experiment Website) pokazany jest poniżej (porównaj z obrazem pokazującym przypadek rozpraszania proton-proton).


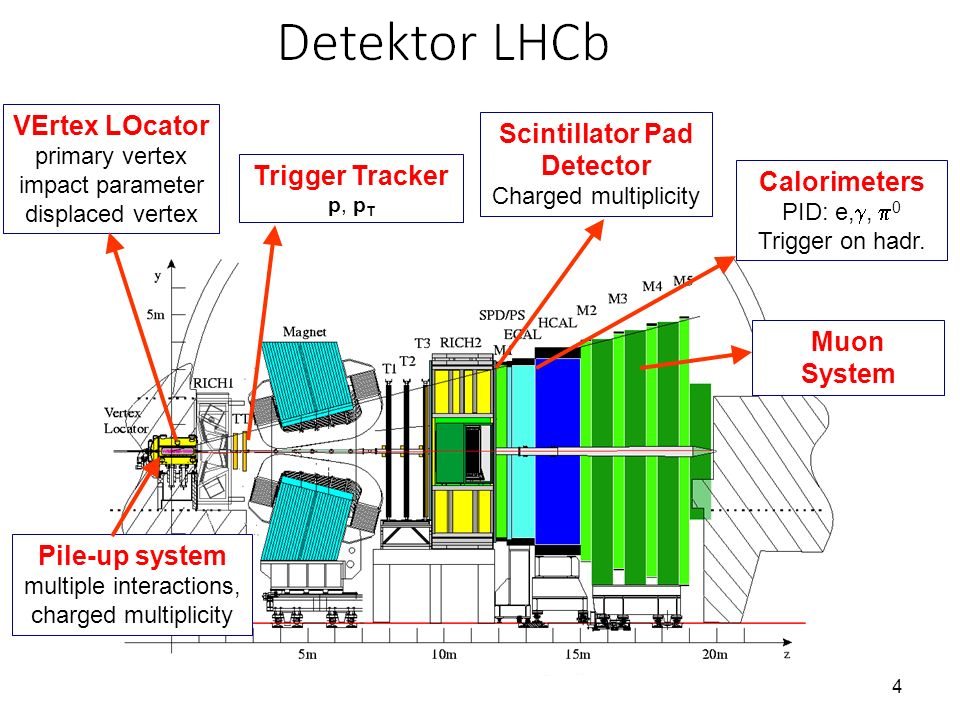
Rysunek 2. Schemat detektora LHCb (przekrój poprzeczny).

LHCb jest jednym z 'Wielkich' detektorów działających obecnie przy akceleratorze LHC w CERN. Zbudowany jest w geometrii spektrometru - nie pokrywa całego kąta bryłowego a jedynie jego mały wycinek. Rozmieszczenie poszczególnych systemów składowych jest standardowe dla dużych uniwersalnych urządzeń hybrydowych. Najbliżej punktu przecięcia wązek protonowych znajdują się detektory śladowe, które są 'lekkie' w sensie długości radiacyjnej X₀. Mówimy również, że detektory śladowe powinny wnosić jak najmniej do ogólnego budżetu materiałowego detektora. System śladowy składa się z detektora wierzchołka (VELO, VErtex LOcator), stacji TT (Trigger Tracker) oraz stacji T1 - T3 (za magnesem dipolowym). Za stacjami T1 - T3 znajudją się kalorymetry: najpierw mamy ECAL (kalorymeter elektromagnetyczy) oraz HCAL (kalorymetr hadronowy). Na końcu znajdziemy komory mionowe. Do układu pomiarowego LHCb wchodzą dodatkowo detektory RICH1/2 (Ring Imaging Cherenkov), które służą do identyfikacji naładowanych hadronów. Nasze ćwiczenie dotyczy badania własności detektora wierzchołka VELO, który znajduje się najbliżej punku rozpraszania. Jest to detektor krzemowy mikro-paskowy, jego konstrukcja pokazana jest na poniższym rysunku.


Rysunek 3. Schemat poglądowy detektora wierzchołka VELO w eksperymencie LHCb. Detektor składa się z dwóch ruchomych 'połówek', które mogą oddalić się od siebie na odległość około 30 mm. Jest to ważne podczas napełniania akceleratora oraz przygotowania stabilinych wiązek. Obie połówki oddzielone są od siebe cienką folią aluminiową.

Częścią aktywną detektora VELO (tam gdzie cząstki naładowane oddziałują z materią!) są sensory krzemowe. Sensory są zorientowane prostopadle do wiązek protonowych i posiadają kształt kołowy (dwa sensory przypominają standardową płytę CD!). Grubość pojedynczego sensora wynosi 300 μm. Liczba kanałów odczytu znajdujaca się na jednym sensorze to 2048. W zależności od sposobu rozmieszczenia kanałów (pasków) na powierzchni sensorów (nazywamy to różnież segmentacją detektora) wyróżniamy dwa typy geometrii: sesory-R oraz sensory-Φ. Schematycznie przedstawione są na Rysunku 4.


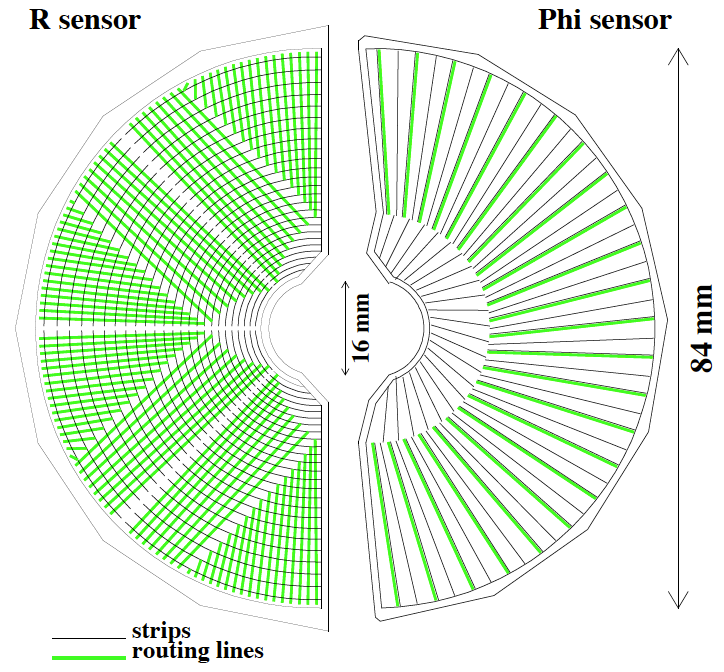
Rysunek 4. Sensory krzemowe detektora VELO typ-R (lewa część rysunku) oraz typ-Φ (prawa część rysunku).

W naszym ćwiczeniu skupimy się na badaniu efektów oddziaływania cząstek naładowanych, pochodzących ze zderzeń protonów w akceleratorze LHC. Poniżej znajduje się opis aspektów technicznych analizy.

Do analizy zostanie użyta próbka symulowanych przypadków rozpraszania proton-proton przy energii wiązki 3,5 TeV (czyli 7 TeV w układzie środka masy). Wygenerowane przypadki (około 25 tysięcy zderzeń proton-proton) zostały przetworzone przez oprogramowanie do modelowania odziaływania z materią GEANT4 (GEANT Website). W kroku tym został użyty dokładny model detektora LHCb, który definiuje położenia oraz skład materiałowy części aktywnych oraz pasywnych wszystkich systemów pomiarowych. Dzięki temu możliwe jest modelowanie numeryczne efektów przejścia cząstek przez spektrometr LHCb, które można zinterpretować jako sygnał elektryczy (symulowany!) jaki zostanie zaobserwowany w danym kanale pomiarowym. W przypadku systemu śladowego sygnały te interpretowane są jako tzw. hity i służą do rekonstrukcji śladów (cząstek). Proces obróbki danych symulowanych przedstawiony jest schematycznie na Rysunku 5.


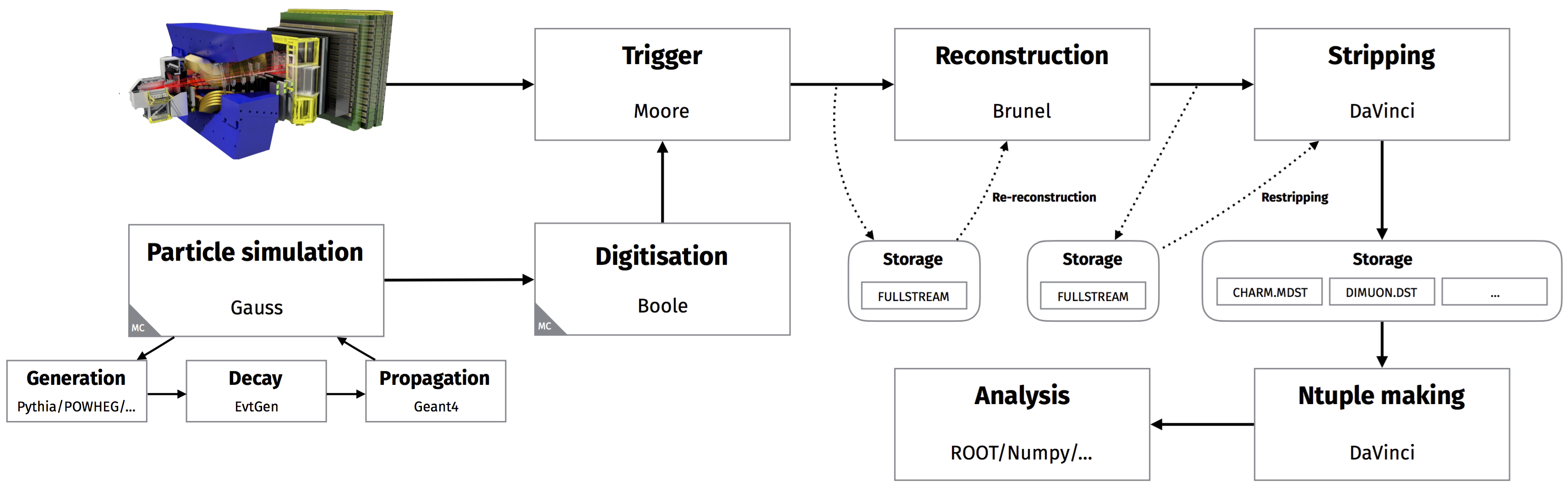
Rysunek 5. Schemat przetwarzania danych (symulowanych oraz 'prawdziwych') dla eksperymentu LHCb.

Z punktu widzenia 'data flow' obróbkę danych można podzielić na dwie odrębne domeny:

• Symulacja - generowanie danych (Generation), rozpad cząstek niestabilnych (Decay), oddziaływanie z materiałem detektora (Propagation). Proces kończy się emulacją elektroniki odczytu poszczególnych detektorów oraz wyprodukowaniem danych w formacie identycznym jak format danych rzeczywistych (Digitisation).

• Dane rzeczywiste produkowane przez detektor - przetwarzane są następnie przez układ wyzwalania, który dokonuje filtrowania przypadków oraz kompresji strumienia danych (Trigger). Dane takie (nazywane często danymi surowymi) podlegają procesowi rekonstrukcji (Reconstruction), podczas którego odtwarzamy topologię poszczególnych przypadków (wierzchołki, ślady). Na końcu dokonujemy analizy fizycznej danych.

Dane, którymi posłużymy się w naszej analizie przeszły wszystkie etapy obróbki jakim podlegają dane symulacyjne (Digitisation). Następnie, zostały one użyte do rekonstrukcji śladów przy pomocy tego samego oprogramowania jakie jest używane do obróki danych rzeczywistych. Na tym etapie wybrane parametry fizyczne zrekonstruowanych śladów zostały zapisane do pliku w formacie root, w postaci relacyjnej bazy danych. Dodatkowo, z uwagi na to że używamy danych symulacyjnych możliwe było zapisanie wybranych 'prawdziwych' (wygenerowanych) parametrów cząstek, których ślady zostały następnie zrekonstruowane. Dzięki temu możemy badać wybrane cechy detektora, takie jak wydajność.

Struktura pliku wejściowego do naszej analizy jest nieco skomplikowana. Wynika to z tego, że chcemy zachować zależności pomiędzy cząstkami wyprodukowanymi w każdym osobnym przypadku. W fizyce wysokich energii stosujemy standardowy format tzw. NTuple (lub N-krotki), który pozwala na zapisanie w jednym rekordzie (odpowiadającym jednemu przypadkowi) danych różnego typu (np. float double, bool, wektory, macierze, itp). W środowisku ROOT utworzenie takiej bazy danych realizuje się poprzez klasę TTree. Otwórzmy plik wejściowy i popatrzmy na jego wnętrze (nie jest to absolutnie konieczne do analizy danych ale pomoże w zrozumieniu odpowiednich partii kodu!).

Do pracy wykorzystame te same konta, które używaliśmy do pracy z pakietem FLUKA. Logujemy się na serwer lhcb1. Po zalogowaniu konfigurujemy środowisko pracy wykonując skrypt setlab-env, który można pobrać z: /datac/storage/opjzm_labo/scripts. Skrypt ustawia ścieżkę dostępu do pliku wejściowego (w formacie .root) oraz umożliwia uruchomienie samego środowiska ROOT. Przykładowy efekt przedstawiony jest na Rysunku 6.


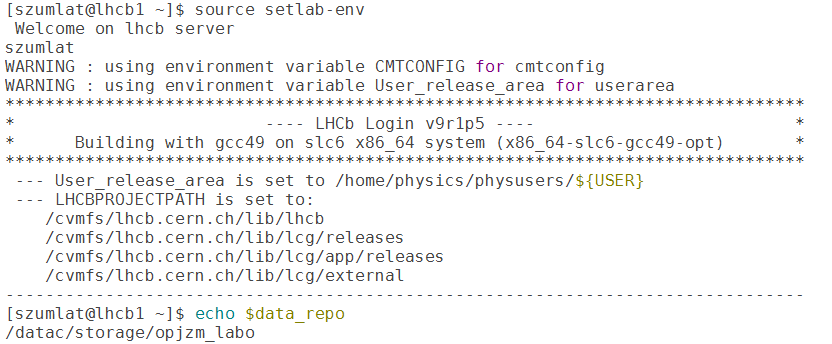
Rysunek 6. Efekt uruchomienia skrytpu konfiguracyjnego. Proszę zwrócić uwagę na zawartość zmiennej data_repo - tam znajduje się plik wejściowy do analizy.

Zbadajmy zawartość i strukturę pliku - uruchamiamy środowisko ROOT poleceniem root ścieżka_do_pliku_z_danymi. Po uruchomieniu środowiska otwieramy przeglądarkę, która pomoże nam nawigować po drzewie katalogów oraz poruszać się wewnątrz pliku wejściowego.


Rysunek 7. Uruchomienie środowiska root oraz przeglądarki TBrowser.

Po uruchomieniu przeglądarki otworzy się okienko - GUI root'a. Posługiwanie się GUI jest czasami przydatne gdy zależy nam na szybkiej ocenie jakości danych lub sprawdzeniu poprawności napisanego kodu do analizy. My będziemy posługiwać się wyłącznie odpowiednim skryptem.


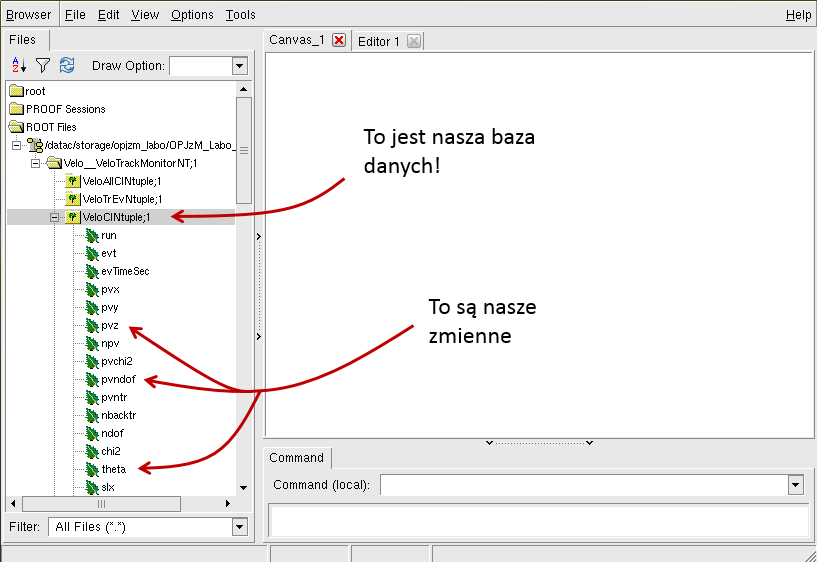
Rysunek 8. Graficzne złącze użytkownika (GUI) w środowisku ROOT.

Przeglądarka zawiera obiekt typu TCanvas, który jest wykorzystywany przy wizualizacji zmiennych fizycznych. Aby zobaczyć go w akcji należy po prostu kliknąć dwa razy na dowolną zmienną zapisaną w drzewie NTupla (zmienne mają nie bez przyczyny kształt liści...).


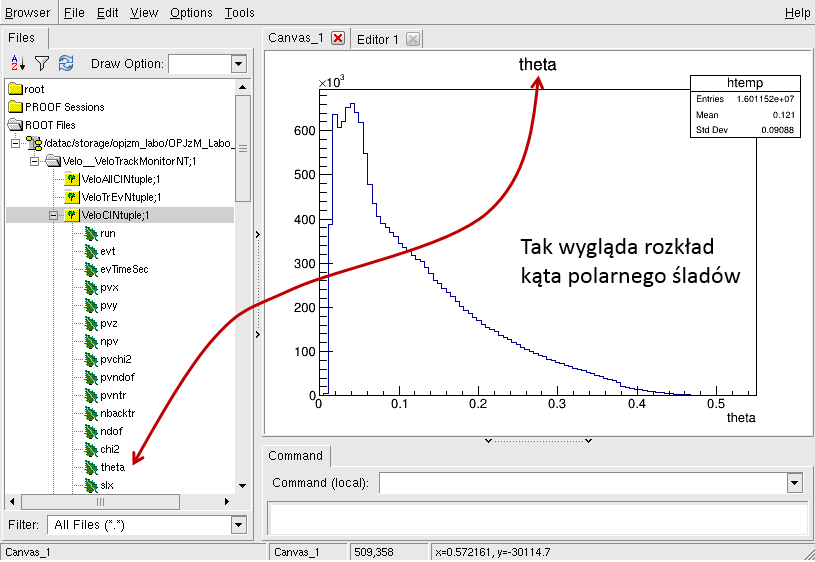
Rysunek 9. Rozkład kąta polarnego zrekonstruowanego śladu w detektorze VELO.

Zamiast 'klikania' możemy napisać skrypt do analizy oraz wizualizacji danych. Skrypt dajne nam do tego znacznie większą elasyczność oraz dostęp do każdego przypadku osobno. Dzięki temu możemy wprowadzać dodatkowe kryteria (tzw. cięcia) do naszej analizy. Skrypt napisany jest w języku c++ (tak jak interpreter ROOT'a) i można go podzielić (logicznie) na trzy części:

• Obsługa We/Wy, połączenie z bazą danych oraz mapowanie zmiennych z bazy na zmienne lokalne (ta część jest w całości dostarczona przez prowadzących zajęcia i na tym etapie nie należy się tym przejmować!)

• Analiza fizyczna - mając dostęp do wszystkich zmiennych w naszym strumieniu danych możemy wykonać analizę (opis zmiennych znajduje się poniżej!)

• Wizualizacja - wyniki naszej pracy chcemy zaprezentować w formie histogramów. Istnieje również możliwość zapisania ich do pliku (dzięki temu, nie będziemu musieli ponownie uruchamiać skryptu do analizy)

Skrypt, o nazwie mc_data_analysis_G4.h(cxx), do analizy można pobrać z /datac/storage/opjzm_labo/scripts i umieścić go w swoim lokalnym katalogu roboczym - np. G4_lab. Aby go uruchomić należy wykonać następującą sekwencję poleceń:


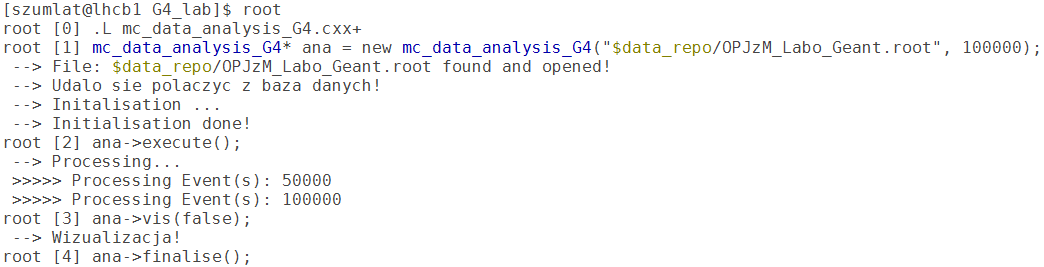
Rysunek 9. Sekwencja poleceń potrzebna do kompilacji oraz uruchomienia analizy.

Skrypt do analizy jest zaimplementowany jako klasa c++, którą można skompilować w środowisku ROOT. Po kompilacji (ładowanie pliku odbywa się przy pomocy komendy .L, natomiast kompilacja jest uruchomiona jeżeli dodamy po nazwie skryptu '+') ROOT utworzy bibliotekę, która automatycznie zostanie dodana do kolekcji znanych obiektów. Możemy następnie utworzyć instancję naszej klasy do analizy i wywołać kolejno funkcje: execute(), vis(false/true) oraz finalise. W tym momencie można funkcję do wizualizacji wywołać jedynie z flagą 'false' - gdyż część programu do zapisywania wyników analizy nie jest zaimplementowana (to jedno z zadań do wykonania dla WAS!). Zobaczmy co podstawowa wersja skryptu może zrobić i zapoznajmy się ze sposobem uzyskania tych wyników!

Po uruchomienu wizualizacji skrypt tworzy dwie kanwy. W pierwszej (drugą zajmiemy się potem) znajdują się dwa histogramy przedstawiające rozkłady kąta polarnego (θ) śladów zrekonstruowanych cząstek na wybranych sensorach oraz rozkład pseudopospieszności (η) w funkcji kąta polarnego śladu. Aby porównać uzyskany rozkład η = η(θ) możemy nałożyć na punkty pomiarowe (pamiętamy, że to jest cały czas symulacja!) funkcję teoretyczną zdefiniowaną jako: η = -ln(θ/2.). Funkcja reprezentująca przebieg teoretyczny ma kolor czerwony. Jak widać zgodność pomiędzy 'pomiarem' a wartością teoretyczną jest bardzo dobra. Aby zrozumieć jak uzyskaliśmy te rysunki musimy przeczytać i zrozumieć kod skryptu do analizy. Zacznijmy od przygotowania zmiennych, które zapisane zostały w NTuplu - w zasadzie zrobimy to samo co zrobiliśmy aby 'wyklikać' histogramy.

• Połączenie (interface) z bazą danych - potrzebna jest nam znajomość ścieżki do katalogu gdzie znajduje się NTuple, jego nazwa oraz ścieżka do struktury danych TTree. Implementacja interfejsu znajduje się w konstruktorze klasy do analizy:

  
  
  Rysunek 10. Kod implementujący interfejs do bazy danych oraz utworzenie wskaźnika do głównej struktury danych (obiekt TTree).
  
  

• Mapowanie zmiennych zapisanych w NTuplu na zmienne lokalne w programie. To proces składający się z kilku kroków - najpierw definiujemy odpowiednią zmienną lokalną, ktra ma być skojarzona ze zmienną z NTupla (typ musi być taki sam, czyli jeżeli mamy zmienną X w NTuplu typu double to musimy stworzyć zmienną lokalną tego samego typu). Dla każdej zmiennej definiujemy również stowarzyszoną zmienną typu TBranch*, która będzie służyła jako adres do odpowiedniej gałęzi obiektu TTree. Na koniec potrzebna jest nam jeszcze nazwa pod jaką zmienna została zapisana w NTuplu. Uff, linijki wyglądają tak:
  
  
  Rysunek 11. Mapujemy zmienną "theta" (to nazwa z NTupla) na zmienną lokalną m_theta. Zmienną lokalną definiujemy jako pole klasy (typ Double_t - to typ ze świata ROOT'a). Następnie definiujemy partnera (gałąź) typu TBranch* o wygodnej nazwie b_theta. Na końcu używamy wskaźnika (interfejsu) do bazy danych i wywołujemy funkcję setBranchAddress("nazwa_zmiennej_w_NTuplu", &zmienna_lokalna, &gałąź).
  
  

• Analiza danych (operacje na zmiennych z NTupla). Zmienne z NTupla możemy korelować, porównywać z innymi zmiennymi, kombinować je tworząc nowe zmienne itp., itd. Zwylke w procesie analizy korzystamy z kryteriów selekcji - czyli badamy zmienne biorąc pod uwagę zachowanie innych zmiennych (to jeszcze trochę zawiłe ale już niedługo...). Kryteria selekcji nazywamy często cięciami. W naszym programie będziemy używać tak zwanych cięć liniowych lub sekwencyjnych. Oznacza to, że będziemy je aplikować po kolei. Innym podejściem jest analiza wielomodalna, gdzie dowolny zbiór cięć można zastosować jednocześnie (tym się nie będziemy zajmować). Wróćmy do rysunków z pierwszej kanwy. Jak narysować rozkład kąta polarnego śladow θ na wybranych sensorach. Musimy mieć zmienną, która reprezentuje zmierzony (zrekonstruowany) kąt dla każdego śladu. Ok, mamy ją nazywa się m_theta. Potrzebujemy jeszcze informacji na temat sensorów. W NTuplu zapisaliśmy zmienną sensnum, która jest właśnie tym czego potrzebujemy! Teraz analiza jest prosta - mysimy przedstawić bazie danych następujące pytanie: podaj mi wartości kąta θ dla każdej cząstki zarejestrowanej na sensorze n. Kod, wygląda tak:
  
  
  Rysunek 12. Analiza danych polega na formułowaniu zapytań logicznych przy użyciu zmiennych zapisanych w NTuplu. Tutaj interesuje nas rozkład kata polarnego śladu dla wybranych sensorów: 10, 15, 25 oraz 35.
  
  Wynik selekcji zapisujemy w kontenerach (histogramach) które mogą być następnie wyświetlone. W naszym przykładzie to: m_th10->Fill( m_theta ). Sposób deklaracji histogramów można zrealizować następująco:
  
  
  Rysunek 13. Deklaracja histogramów jednowymiarowych (obiekty typu TH1F/D - w zależności czy chcemy w nich przechowywać zmienne typu Float_t czy Double_t).
  
  

Znając juz technologię analizy, możemy zająć się bardziej skomplikowanym przypadkiem - zależnością pseudopospieszności od kąta polarnego śladu. Oczywiście będą nam potrzebne zmienne zawierające te wielkości 'zmierzone' dla każdego śladu (cząstki). Pseudopospieszność jest wygodną miarą kąta pod jakim obserwujemy cząstkę. Z uwagi na własności transformacyjne zmienna ta jest powszechnie używana w fizyce wysokich energii. Jest zefiniowana w ten sposób, że dla małych kątów osiaga duże wartości i maleje wraz ze wzrostem kąta osiągając 0 dla 90 stopni. Mówimy na przykład, że eksperyment LHCb jest eksperymentem 'fizyki do przodu' (forward physics), czyli że jest zdolny do rejestracji cząstek biegnących pod małymi kątami w stosunku do osi wiązki. Kod, który służy do selekcji 'przypadków' wygląda następująco:

Rysunek 14. Kod do selekcji wartości pseudopospieszności. Do wyczyszczenia próbki potrzebujemy odpowiednich cięć (por. opis poniżej).

Poza zmiennymi które chcemy 'narysować' używamy również zmiennych 'czyszczących':

• m_backtr - liczba cząstek (śladów) poruszających się w tylną pół-sferę. Pamiętamy, że LHCb jest wykonany jako spektormet jednoramienny o ograniczonym kącie bryłowym. Ale fizyka 'nie wie' o tym i złośliwie produkuje cząstki z takim samym prawdopodobieństwem do przodu jak i do tyłu. My jesteśmy zainteresowani jedynie przypadkami 'do przodu' dlatego że mam mamy nasz detektor. Użyjemy więc tej zmiennej, która odpowiada liczbie śladów do tyłu, do usunięcia przypadków tego typu

• Poza śladami pochodzącymi z wierzchołka pierwotnego (tam gdzie nastąpiło oddziaływanie proton-proton) nasza próbka zawiera również rozpady wtórne oraz oddziaływania z materiałem detektora. Takie przypadki też będziemy uważać za kontaminację i usuniemy je przy pomocy zmiennej m_isPrimaryVertex_mc, która jest flagą oznaczającą, że dana cząstka powstała w miejscu oddziaływania protonów (lub pochodzi z rozpadu rezonansu - por. opis powyżej).

Na drugiej kanwie mamy 'tomografię' detektora VELO wykonaną przy pomocy wierzchołków hadronowych to znaczy miejsc w których doszło do oddziaływania nieelastycznego z materiałem detektora (sensory oraz folia aluminiowa). Aby uzyskać rysunek używamy zmiennych oznaczających składową z, wzdłuż osi wiązki, oraz x prostopadłą do osi wiązki. Proszę samodzielnie przeanalizować jakie cięcia zostały użyte w selekcji przypadków. Na rysunek nałożono również odpowiednie współrzędne położenia wierzchołków pierwotnych (czerwone punkty).

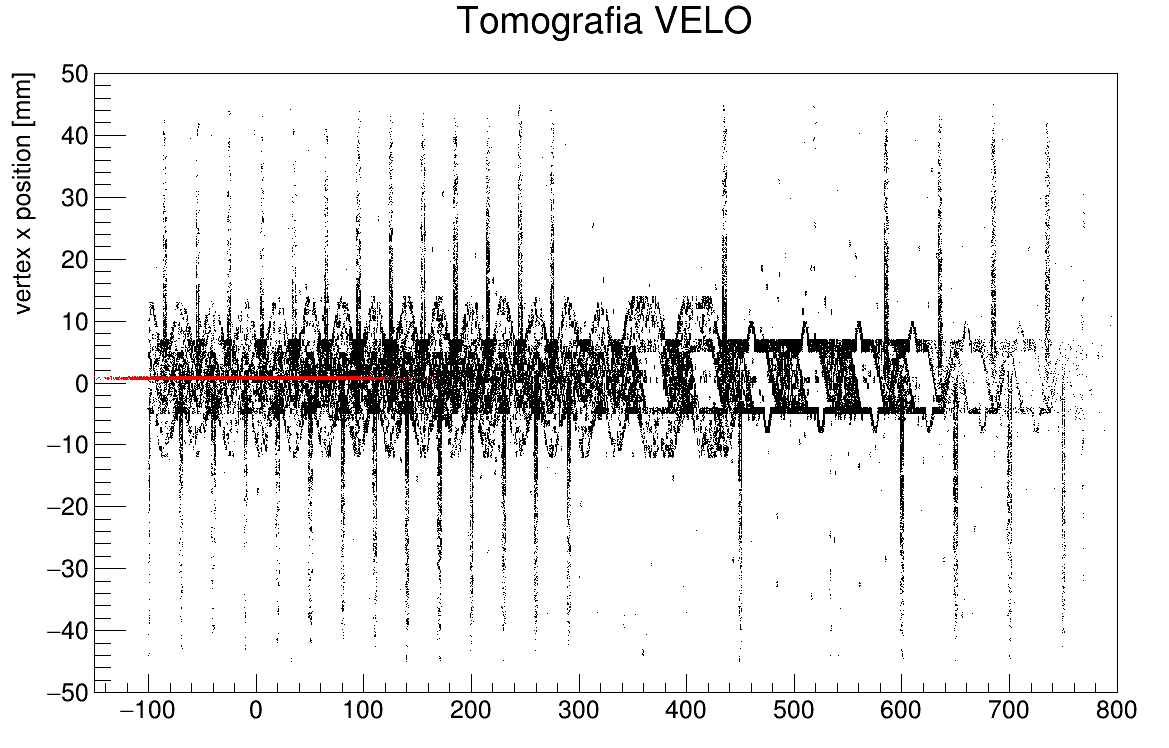
Rysunek 15. 'Tomografia' VELO przy użyciu wierzchołków oddziaływania nieelastycznego cząstek z materiałem detektora.

Wykorzystując przykładowy skrypt proszę wykonać (dodając nowe kanwy!):

• Rozkłady pędów (zmienna p w NTuplu) dla wybranych 4 sensorów, proszę następnie rozkłady porównać poprzez superpozycję (tak jak w przykładzie z rozkładami kąta).

• Czy istnieje korelacja pomiędzy pędem cząstki oraz jej pędem poprzecznym? Pęd poprzeczny to składowa wektora pędu w kierunku prostopadłym do osi zderzających się wiązek protonowych.

• Dopasowanie rozkładu zdeponowanej energii (zmienna adcsum) używając modelu Landaua.

• Rozkład profilowy - zależność pomiędzy rozmiarem klastra a kątem padania cząstki. Klasty to 'obraz' oddziaływania zrekonstruowany bezpośrednio przez sensor. Dana cząstka może 'pobudzić' do kilku (maksymalnie 4) sąsiednich kanałów pomiarowych. Przewidujemy, że im większy kąt padania śladu - tym większy rozmiar klastra (cząstka spędza w krzemie więcej czasu i deponuje więcej ładunku na dłuższej drodze).

• Proszę zaimplementować, korzystając z dokumentacji ROOT'a ROOT Doc, funkcjonalność pozwalającą na zapisywanie histogramów do pliku po zakończeniu analizy.

Porady praktyczne i uwagi

• Jeżeli wykonujemy nowy rysunek, bardzo często chcemy dostać wynik szybko, aby sprawdzić czy dobrze zadeklarowaliśmy histogramy oraz czy wybraliśmy odpowiednie cięcia. Wtedy można uruchomić skrypt wykorzystując tylko część przypadków - można to zrobić podając do konstruktora (jako drugi argument) liczbę przypadków do obróbki.

• Deklaracje kanw oraz rysowanie histogramów zaimplementowane jest w metodzie mc_data_analysis_G4::vis(Bool_t save). Można ją uruchomić od razu podczas wykonywania metody execute(). Parametr oznacza czy zapisać histogramy czy nie - nie chcemy tego robić za każdym razem kiedy uruchamiamy skrypt - lepiej zapisać gotowe już rysunki.

Celem projektu jest zbadanie oraz dyskusja różnych aspektów oddziaływania cząstek naładowanych, wyprodukowanych w zderzeniach proton-proton przy energii LHC, z materiałem detektora wierzchołka eksperymentu LHCb. W sprawozdaniu powinny znaleźć się następujące części:

• Analiza energii zdeponowanej w sensorach krzemowych (zmienna adcsum). Teoria podpowiada nam, że kształt rozkładu energii zdeponowanej w cienkim absorberze (grubość sensorów VELO wynosi 300 μm) powinna być podobna do rozkładu Landaua. W rzeczywistości okazuje się, że sam model Landaua nie jest w stanie opisać poprawnie takiego rozkładu energii. Wyjaśnienie tego faktu opiera się na uwzględnieniu efektów pochodzących również od elektroniki odczytu (szumy). W konsekwencji dobrym modelem, który opisuje rozkład energii w naszych sensorach krzemowych jest splot rozkładu Landaua oraz rozkładu normalnego. Korzystając z przykładowej implementacji (LanGaus) dopasuj model LanGaus do zmierzonych rozkładów na kilku wybranych sensorach.

• Analiza energii zdeponowanej w funkcji energii cząstki. Wykorzystaj do tego zmienną partEnergy_mc. Czy można użyć detektora wierzchołka do identyfikacji cząstek? (por. również wykład). Porównaj z rozkładami energii zdeponowanej (adcsum) w funkcji energii danego typu cząstek (w tym celu użyj zmiennej PID_mc - Particle IDentification, lista cząstek oraz odpowiadające im numery PDG - Particle Data Group, można znaleźć tutaj PDG Particle List).

• Teoria Landaua zakłada, że charakterystyczny rozkład energii zdeponowanej w cienkim absorberze jest obserwowany dla cząstek monochromatycznych (czyli o tej samej energii). Oczywiście nie jest to spełnione w naszym przypadku, gdzie spektrum energii cząstek jest bardzo szerokie. Dokonaj analizy (selekcja oraz dopasowanie modelu LG) rozkładów energii zdeponowanej w funkcji energii cząstek. Dokonaj w tym celu podziału widma energii na biny - szerokość danego binu energii zależeć będzie od liczby cząstek w rozkładzie energii.

• Zbadaj, jak zachowuje się rozkład energii zdeponowanej w funkcji kąta padania śladu zarejestrowanego przez detektor VELO. Teoria Landaua zakłada, że wszystkie cząstki penetrujące materiał absorbera padają na niego pod tym samym kątem. Podobnie jak w przypadku energii cząstek, nie jest to prawdą dla naszej próbki, gdzie rozkłady kąta śladu są szerokie. Cząstki biegnące pod dużymi kątami 'spędzają' w krzemie więcej czasu niż cząstki penetrujące sensory pod małymi kątami. Spodziewamy się więc, że energia zeponowana powinna rosnąć w funkcji kąta polarnego śladu. Dokonaj analizy zachowania rozkładu energii zdeponowanej w funkcji kąta padania śladu.

• Punkt z gwiazdką (nieobowiązkowy dla chętnych). Czy możemy, posiadając NTuple, wyznaczyć kanoniczną zależność Bethe-Blocha?