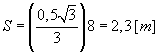Temat 18: Ruch złożony
18.1. Ruch punktu: bezwzględny, względny, unoszenia
Przy rozpatrywaniu ruchu punktu
lub ciała w przestrzeni zakładaliśmy dotychczas, że ruch ten badamy względem
pewnego układu odniesienia, który traktowaliśmy jako nieruchomy.
W ruchu tym ruch każdego punktu był nieruchomy.
W rzeczywistości układy odniesienia, które przyjmowaliśmy za nieruchome,
mogą poruszać się względem innego układu odniesienia. Wówczas ruch punktu
można uważać za ruch punktu złożony z ruchu unoszenia układu ruchomego
i ruchu punktu względem układu ruchomego.
W praktycznych obliczeniach możemy przyjmować, że układ nieruchomy jest
związany z Ziemią lub ze Słońcem.
Za przykład ruchu złożonego niech posłuży ruch pasażera (ruch względny)
w wagonie jadącego pociągu. Dokładny opis ruchu tego pasażera wymaga uwzględnienia
ruchu wagonu (ruchu unoszenia) względem Ziemi.
Ruch punktu M względem układu nieruchomego Oxyz
nazywamy ruchem bezwzględnym.
Ruch punktu M względem układu ruchomego
(względnego) 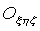 nazywamy
ruchem względnym.
nazywamy
ruchem względnym.
Ruch punktu M, jaki wykonałby on względem układu nieruchomego Oxyz,
gdyby go w danej chwili sztywnie związać z układem ruchomym (względnym) 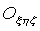 , nazywa się ruchem unoszenia.
, nazywa się ruchem unoszenia.
Ruch unoszenia można także zdefiniować jako ruch układu ruchomego względem
układu nieruchomego. Przyjmijmy nieruchomy układ współrzędnych O1xyz oraz ruchomy układ współrzędnych
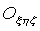 (układ ruchomy, którego osie stale zmieniają swoje położenie) i punkt
M poruszający się dowolnie w układzie ruchomym (rys.18.1).
(układ ruchomy, którego osie stale zmieniają swoje położenie) i punkt
M poruszający się dowolnie w układzie ruchomym (rys.18.1).
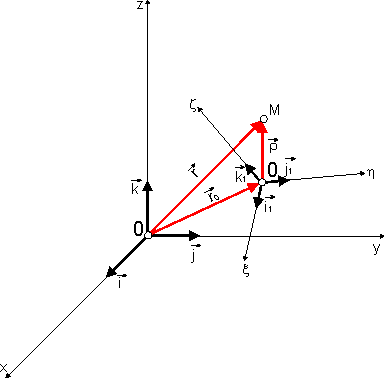
Rys.18.1
Wprowadźmy wektor-promień 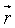 punktu M w układzie nieruchomym, wektor-promień
punktu M w układzie nieruchomym, wektor-promień 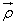 punktu M w układzie ruchomym i wektor-promień
punktu M w układzie ruchomym i wektor-promień 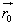 początku ruchomego układu współrzędnych. Wówczas położenie punktu
M w układzie O1xyz określa równanie wektorowe:
początku ruchomego układu współrzędnych. Wówczas położenie punktu
M w układzie O1xyz określa równanie wektorowe:
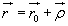 (18.1)
(18.1)
Ponieważ
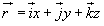 ,
,
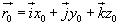 ,
,
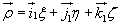 ,
,
gdzie 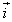 ,
,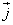 ,
,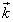 są wektorami jednostkowymi nieruchomego układu współrzędnych, a
są wektorami jednostkowymi nieruchomego układu współrzędnych, a 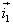 ,
,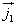 ,
,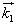 - wektorami jednostkowymi ruchomego układu współrzędnych.
- wektorami jednostkowymi ruchomego układu współrzędnych.
Po podstawieniu powyższych równań do równania (18.1) otrzymamy :
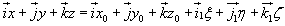 (18.2)
(18.2)
Mnożąc skalarnie równanie
(18.2),
kolejno przez
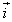
,
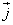
,
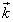
, otrzymujemy współrzędne punktu w układzie bezwzględnym w postaci:
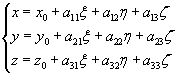 (18.3)
(18.3)
a mnożąc przez 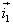 ,
,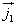 ,
,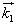 otrzymujemy współrzędne w układzie względnym w postaci :
otrzymujemy współrzędne w układzie względnym w postaci :
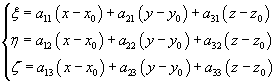 (18.4)
(18.4)
W powyższych równaniach 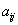 oznaczają zmienne cosinusy kierunkowe kątów między osiami bezwzględnego
i względnego układu współrzędnych, na przykład
oznaczają zmienne cosinusy kierunkowe kątów między osiami bezwzględnego
i względnego układu współrzędnych, na przykład
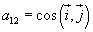 ,
, 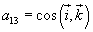 .
.
Pomiędzy dziewięcioma cosinusami istnieje 6 znanych związków:
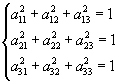 ( 18.5a)
( 18.5a)
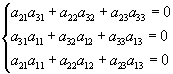 (18.5b)
(18.5b)
18.2. Prędkość i przyspieszenie w
ruchu złożonym
Prędkość punktu w ruchu złożonym
Zajmijmy się wyznaczeniem związku między prędkością w ruchu względnym
a prędkością tego samego punktu w ruchu bezwzględnym.
Prędkość punktu M względem układu nieruchomego
współrzędnych Oxyz nazywamy
prędkością bezwzględną (absolutną) i oznaczamy
ją symbolem 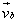 . Prędkość punktu M względem ruchomego układu współrzędnych nazywamy
prędkością względną i oznaczamy symbolem
. Prędkość punktu M względem ruchomego układu współrzędnych nazywamy
prędkością względną i oznaczamy symbolem 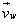 .
.
Prędkość punktu M sztywnie związanego z układem ruchomym 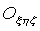 względem układu nieruchomego Oxyz nazywamy prędkością unoszenia i oznaczamy ją symbolem
względem układu nieruchomego Oxyz nazywamy prędkością unoszenia i oznaczamy ją symbolem 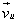 . Możemy także powiedzieć, że prędkością unoszenia punktu M w
danej chwili nazywamy prędkość punktu złączonego z układem ruchomym i pokrywającego
się w tej chwili z punktem M. Różniczkując względem czasu równanie
. Możemy także powiedzieć, że prędkością unoszenia punktu M w
danej chwili nazywamy prędkość punktu złączonego z układem ruchomym i pokrywającego
się w tej chwili z punktem M. Różniczkując względem czasu równanie
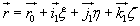 ,
,
otrzymujemy :
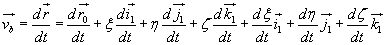 .
(18.6)
.
(18.6)
Bezwzględna prędkość punktu M pokryje się z prędkością unoszenia,
jeżeli w chwili t 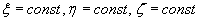 . Wówczas z równania (18.6) otrzymamy
:
. Wówczas z równania (18.6) otrzymamy
:
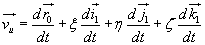 . (18.7)
. (18.7)
Prędkość względna punktu M pokryje się z prędkością bezwzględną,
jeżeli unieruchomiony układ 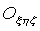 . Otrzymamy wówczas:
. Otrzymamy wówczas:
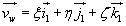 . (18.8)
. (18.8)
Równanie
(18.6) można więc zapisać w postaci:
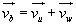 (18.9)
(18.9)
Prędkość bezwzględna punktu
M jest sumą geometryczną prędkości unoszenia i prędkości względnej.
Wprowadzając nieskończenie mały kąt obrotu wektora 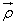 względem jego początku i jako prędkość kątową
względem jego początku i jako prędkość kątową 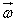 , możemy obliczyć składową prędkości jego końca:
, możemy obliczyć składową prędkości jego końca: 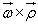 , a następnie obliczyć prędkość unoszenia punktu M (rys. 18.2):
, a następnie obliczyć prędkość unoszenia punktu M (rys. 18.2):
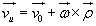 (18.10)
(18.10)
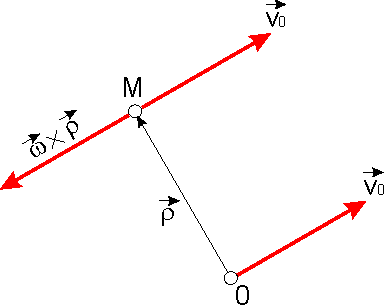
Rys.18.2
Przyspieszenie
punktu w ruchu złożonym
Analogicznie jak przy obliczaniu prędkości określimy
przyśpieszenie bezwzględne 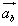 , unoszenia
, unoszenia 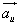 i względne
i względne 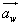 . Różniczkując (18.6) względem czasu, znajdujemy przyśpieszenie bezwzględne
. Różniczkując (18.6) względem czasu, znajdujemy przyśpieszenie bezwzględne
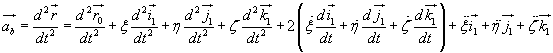 . ( 8.11)
. ( 8.11)
Rozpatrując wzór (18.11) podobnie jak (18.6
), otrzymujemy:
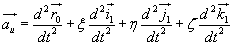 , (18.12)
, (18.12)
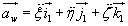 .
(18.13)
.
(18.13)
Pozostałe człony oznaczamy
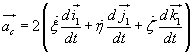 (18.14)
(18.14)
i nazywamy przyśpieszeniem Coriolisa. Wzór (18.11) można ostatecznie zapisać
w postaci
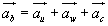 . (18.15 )
. (18.15 )
Przyśpieszenie bezwzględne
punktu jest sumą geometryczną przyśpieszeń: unoszenia, względnego i Coriolisa.
Unieruchamiając wektor 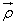 w układzie ruchomym można obliczyć przyśpieszenie unoszenia, różniczkując
względem czasu wyrażenie (18.8)
w układzie ruchomym można obliczyć przyśpieszenie unoszenia, różniczkując
względem czasu wyrażenie (18.8)
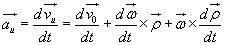 . (18.16)
. (18.16)
Ponieważ:
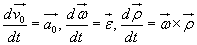 ,
,
więc
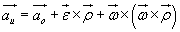 .
(18.17)
.
(18.17)
Biorąc pod uwagę zależność Poissona:
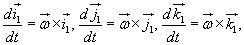
przyśpieszenie Coriolisa można zapisać w postaci
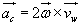 . (18.18)
. (18.18)
Przyśpieszenie Coriolisa jest podwojonym iloczynem
wektorowym prędkości kątowej i prędkości względnej.
Przyśpieszenie Coriolisa jest równe
zeru, jeżeli 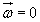 , albo
, albo 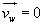 , lub jeżeli wektor
, lub jeżeli wektor 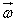 jest równoległy do
jest równoległy do 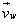 . Przyśpieszenie to jest wektorem prostopadłym do płaszczyzny utworzonej
przez wektory
. Przyśpieszenie to jest wektorem prostopadłym do płaszczyzny utworzonej
przez wektory 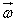 oraz
oraz 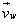 . Wartość wektora
. Wartość wektora 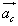 wynosi
wynosi
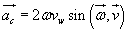 . (18.19)
. (18.19)
Zwrot wektora określamy na podstawie
wzoru (6.18)
tak, aby patrząc na niego widzieć obrót wektora 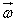 do wektora
do wektora 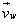 w kierunku przeciwnym do obrotu wskazówek zegara (układ prawoskrętny, rys. 18.3).
w kierunku przeciwnym do obrotu wskazówek zegara (układ prawoskrętny, rys. 18.3).
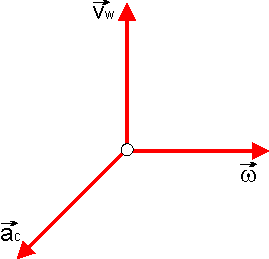
Rys. 18.3
Przykład:
Tarcza kołowa o promieniu R = 2m obraca się w płaszczyźnie pionowej
względem punktu O z prędkością kątową 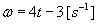 . Po torze prostoliniowym odchylonym o kąt
. Po torze prostoliniowym odchylonym o kąt 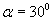 posuwa się punkt M (rys 18.4), którego
droga
posuwa się punkt M (rys 18.4), którego
droga 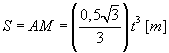 . W chwili t = 0 [s] punkt M znajdował się w punkcie A.
Obliczyć prędkość i przyśpieszenie bezwzględne punktu M po czasie
t = 2 [s].
. W chwili t = 0 [s] punkt M znajdował się w punkcie A.
Obliczyć prędkość i przyśpieszenie bezwzględne punktu M po czasie
t = 2 [s].
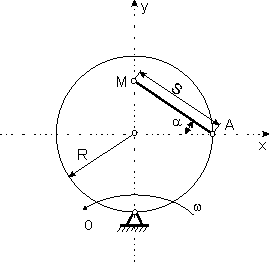
Rys. 18.4 )
Rozwiązanie:
Po czasie t = 2 [s] punkt M znajdował się w
punkcie przecięcia się prostoliniowego toru w ruchu względnym z pionową
średnicą tarczy
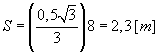
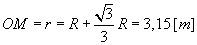
Prędkość bezwzględna punktu M w ruchu złożonym:
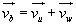
Prędkość w ruchu obrotowym unoszenia wynosi:
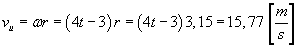
Prędkość w ruchu względnym ( prostoliniowym ) wynosi:
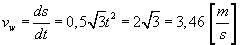
Bezwzględna prędkość punktu M wynosi:
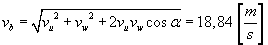
Przyśpieszenie bezwzględne punktu M w ruchu złożonym:
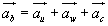
Wartość składowych przyśpieszenia punktu M w ruchu unoszenia:
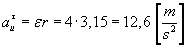 ,
, 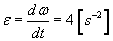
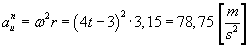
Wartość przyśpieszenia punktu M w ruchu względnym wynosi:
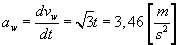
Przyśpieszenie Coriolisa:
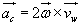
Wartość przyśpieszenia Coriolisa wynosi:
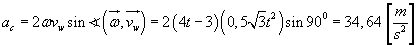
Przyjmujemy w punkcie M płaski prostokątny układ
współrzędnych i obliczamy składowe przyśpieszenia punktu M w tym
układzie.
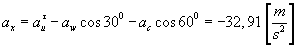
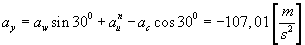
Wartość przyśpieszenia bezwzględnego punktu M
obliczamy za wzoru:
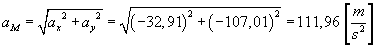
Pytania i ćwiczenia sprawdzające
1. Co to jest ruch złożony?
2. Co to jest ruch bezwzględny?
3. Co to jest ruch względny?
4. Co to jest ruch unoszenia?
5. Prędkość bezwzględna w ruchu złożonym
( wzór ).
6. Przyśpieszenie bezwzględne w ruchu
złożonym.
7. Przyśpieszenie Coriolisa ( definicja
).
8. Wartość przyśpieszenia Coriolisa.
9. Omówić kiedy nie występuje przyśpieszenie
Coriolisa ( tzn. kiedy jest ono równe zeru ).
Ćwiczenia:
1. Mając dane równania ruchu względnego punktu M
i unoszenia płytki w kształcie trójkąta prostokątnego, wyznaczyć dla 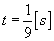 prędkość i przyśpieszenie bezwzględne punktu M rys 18.5) mając następujące dane:
prędkość i przyśpieszenie bezwzględne punktu M rys 18.5) mając następujące dane: 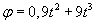 ,
, 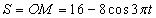 , gdzie S wyrażono w [cm], t w [s], a
, gdzie S wyrażono w [cm], t w [s], a 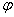 w [rad],
w [rad], 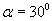 .
.
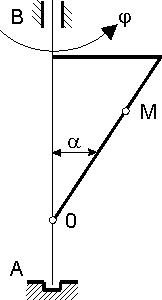
Rys. 18.5
Odpowiedź: 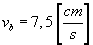 ,
, 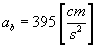 .
.
2. Punkt K (rys 18.6) porusza się po obwodzie tarczy zgodnie z równaniem 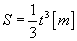 , zaś tarcza o promieniu r = 1 [m] obraca się ze stałą prędkością kątową
, zaś tarcza o promieniu r = 1 [m] obraca się ze stałą prędkością kątową
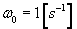 względem osi pionowej. Obliczyć prędkość i przyśpieszenie bezwzględne
względem osi pionowej. Obliczyć prędkość i przyśpieszenie bezwzględne
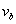 ,
, 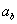 punktu K w chwili
punktu K w chwili 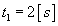
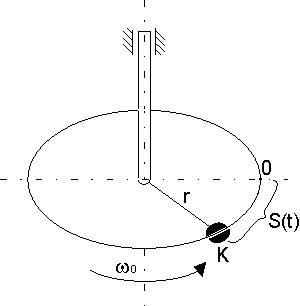
Rys. 18.6
Odpowiedź: 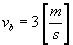 ,
, 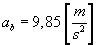 .
.

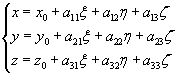 (18.3)
(18.3)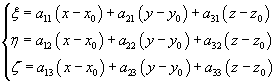 (18.4)
(18.4)
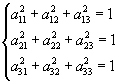 ( 18.5a)
( 18.5a)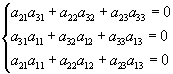 (18.5b)
(18.5b)
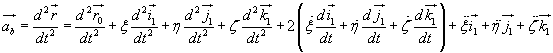 . ( 8.11)
. ( 8.11)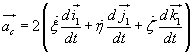 (18.14)
(18.14)
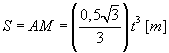 . W chwili t = 0 [s] punkt M znajdował się w punkcie A.
Obliczyć prędkość i przyśpieszenie bezwzględne punktu M po czasie
t = 2 [s].
. W chwili t = 0 [s] punkt M znajdował się w punkcie A.
Obliczyć prędkość i przyśpieszenie bezwzględne punktu M po czasie
t = 2 [s].