Temat 19: Ruch płaski bryły

19.1. Wstęp

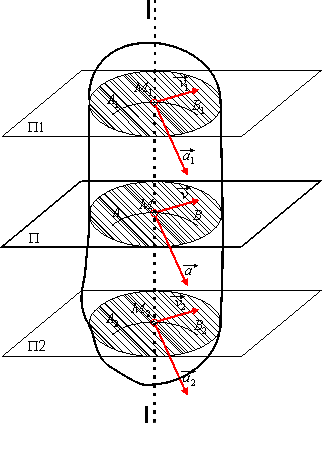
Jeżeli wszystkie punkty bryły poruszają się w płaszczyznach równoległych do pewnej płaszczyzny nieruchomej, to ruch bryły jest ruchem płaskim. Płaszczyzny, w których poruszają się się punkty bryły, nazywają się płaszczyznami kierowniczymi lub prowadzącymi.

 W ruchu płaskim wszystkie punkty bryły leżące na prostej l-l do wymienionych płaszczyzn mają jednakowe trajektorie, prędkości i przyspieszenia (rys. 19.1a):

Odnośnie do torów, prędkości i przyspieszeń innych punktów w ogólnym przypadku nie możemy nic powiedzieć. Zależnie od ruchu należy te wielkości odpowiednio wyznaczyć.

Jak z powyższego wynika, przy ruchu płaskim bryły wystarczy badać ruch figury płaskiej, będącej przekrojem bryły równoległym do płaszczyzny kierowniczej.

Przemieszczenie figury płaskiej można rozłożyć na przemieszczenie ruchem postępowym unoszenia, to jest przemieszczenia układu O_x1y1, którego początek przyjęto w dowolnym punkcie   O figury płaskiej, i na przemieszczenie ruchem obrotowym względnym wokół tego punktu; jest to obrót układu związanego z figurą płaską wokół punktu O (rys. 19.1b).

                Rys. 19.1a                                                                                             Rys. 19.1b

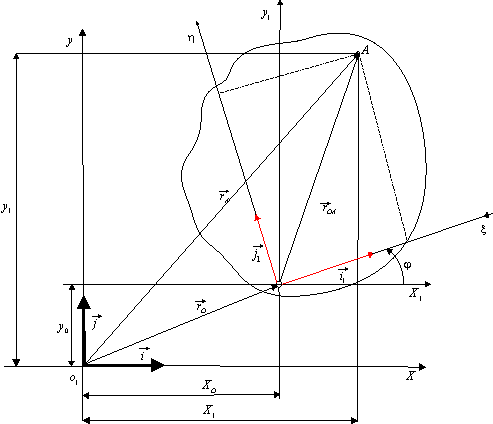
W układzie współrzędnych O_1xypołożenie  figury płaskiej można określić podając współrzędne O(x₀,y₀) oraz kąt obrotu układu względem układu O_1xy.

Równanie ruchu płaskiego zapisujemy w postaci:

                                                                                                                                                       (19.1)                                      
A więc bryła w ruchu płaskim ma 3 stopnie swobody ( może mieć także 2 lub 1). Położenie dowolnego punktu, na przykład punktu A figury płaskiej w układzie nieruchomym O_xy, wyznacza wektor-promień wodzący .

                                                                                                                                                                                                                                                                                                                                                                                                                                   (19.2)
gdzie jest wektorem- promieniem wodzącym bieguna O, a - wektorem-promieniem wodzącym punktu A w układzie ruchomym stałym co do wartości a zmiennym co do kierunku:

                                                                                                                                                                                  (19.3)                                                                                                                                                                                                                                                    Podstawiając wzór (19.3) do (19.2) otrzymamy:

.                                                                                                                                                                      (19.4)                                                                                                                                                                                                                                           
 Rzutując (19.4) na osie układu O_xy (rys. 19.1b) otrzymujemy:
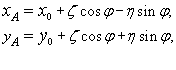                                                                                                                                                             (19.5)

gdzie i są stałymi, a pozostałe wielkości we wzorach (19.5) są funkcjami czasu.
Rugując z równań (19.5) czas t, otrzymujemy trajektorie punktu A.

19.2. Skończony i chwilowy środek obrotu

Twierdzenie:

Jeżeli figura płaska porusza się w swej płaszczyźnie, to z każdego położenia w inne położenie daje się przesunąć przez obrót dokoła punktu leżącego w tej płaszczyźnie, zwanego środkiem obrotu skończonego (przesunięcie równolegle można uważać za obrót punktu leżącego w nieskończoności).

Dowód:
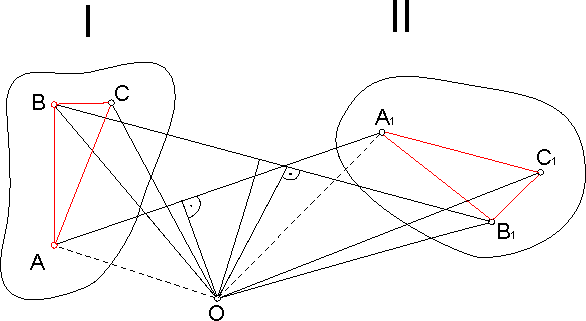
    Przyjmijmy, że trzy punkty A, B, C, (rys. 19.2) oznaczają położenie początkowe w chwili t₀, punkty A₁, B₁, C₁, położenie w chwili t₁. Wykreślamy odcinki AA₁, BB₁ i wyznaczamy punk O leżący na przecięciu symetralnych tych odcinków. Wykażemy, że przemieszczenie figury płaskiej można zrealizować przez obrót dookoła punktu O. Z przeprowadzonej konstrukcji wynika że: AO=AO₁, BO=B₁O, a więc przemieszczenie od A do A₁  i  od B do B₁ można wykonać po łuku koła o środku w punkcie O. Również łatwo można wykazać że, Pozostaje wykazać, że dowolny inny punkt C można przesunąć do C₁ również po łuku koła o środku w punkcie O. Trójkąty   są przystające, ponieważ BC=B₁C₁, OB=OB₁ i zaznaczone kąty są równe. Czyli, że OC=OC1, co oznacza, że punkt C przechodzichodzi do punktu C₁ po łuku koła o środku w punkcie O. Punkt O jest środkiem skończonego obrotu figury płaskiej.

Rys 19.2

Jeżeli figura płaska w chwili t₀ zajmuje położenie I, a w chwili t₁ położenie II (rys. 19.2) to można wyznaczyć środek skończonego obrotu. Jeżeli bierzemy coraz bliższe położenie, tak że t₁ t_o , to dla każdego z tych położeń można wyznaczyć środek skończonego obrotu. Dla coraz bliższych położeń, położenie środka skończonego obrotu zmierza do pewnego położenia granicznego. Graniczne położenie środka skończonego obrotu, gdy t₁ t₀ , nazywamy chwilowym środkiem obrotu w chwili t₀.

   19.3. Sposoby wyznaczenia chwilowego środka obrotu

1. Znana jest prędkość punktu C i prędkość kątowa figury płaskiej (rys.19.3). Chwilowy środek obrotu znajduje się na prostej prostopadłej,               poprowadzonej z punktu C, do prędkości   tego punktu w odległości  . Kierunek prostej prostopadłej znajdujemy obracając wektor o kąt w kierunku obrotu.

 
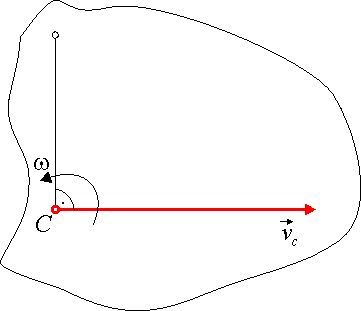
Rys 19.3

2. Znane są kierunki prędkości dwóch punktów A i B płaskiej figury. Chwilowy środek obrotu znajdujemy na przecięciu się prostych prostopadłych, poprowadzonych z punktów A i B, do kierunków prędkości  tych punktów (rys 19.4).

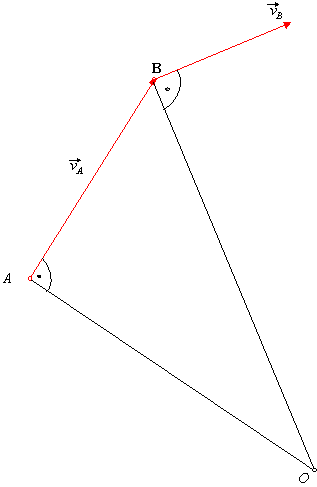
Rys 19.4

3. Prędkości dwóch punktów A i  B o zgodnych zwrotach i różnych wartościach liczbowych są do siebie równoległe i prostopadłe do odcina AB. Chwilowy środek obrotu znajduje się na przedłużeniu odcinaka AB w stronę tego punktu, którego prędkość jest mniejsza. Odległość tych punktów do chwilowego środka obrotu jest proporcjonalna do prędkości punktów. W celu znalezienia chwilowego środka obrotu muszą być znane kierunki i wartości prędkości punktów A i B (rys. 19.5).

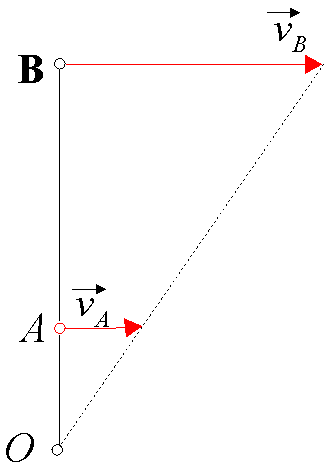
Rys 19.5

4. Prędkość dwóch punktów A i B maja  zwroty przeciwne, są do siebie równoległe i prostopadłe do odcinka AB. Chwilowy środek obrotu leży na odcinku AB i dzieli go na odcinki proporcjonalne do prędkości . W celu znalezienia chwilowego środka obrotu muszą być znane kierunki i wartości prędkości punktów A i B (rys. 19.6).

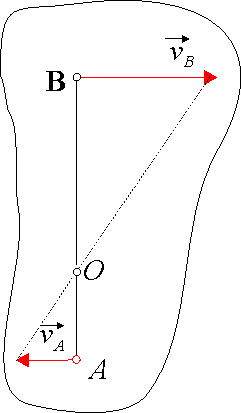
Rys 19.6

5. Płaska figura toczy się bez poślizgu po nieruchomej krzywej (rys. 19.7). Chwilowy środek obrotu O znajduje się wówczas w punkcie styku figury płaskiej z krzywą .

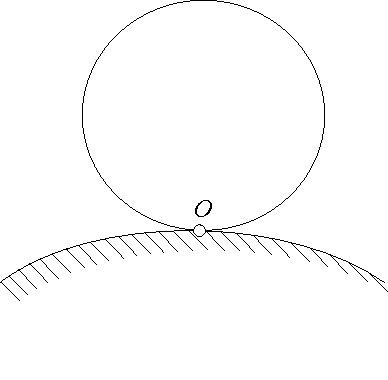
Rys 19.7

6. Jeżeli prędkość dwóch punktów A i B figury płaskiej są sobie równe co do wartości, mają zgodne zwroty i są do siebie równoległe (rys. 19.8) lub są prostopadłe do odcinka AB (rys.19.9), to chwilowy środek obrotu leży w nieskończoności. Prędkość kątowa figury w danej chwili jest równa zeru. Ruch w tym przypadku figury płaskiej nazywa się chwilowym ruchem postępowym. Prędkość wszystkich punktów w danej chwili jest równa. Położenie chwilowego środka obrotu może być znalezione analitycznie.

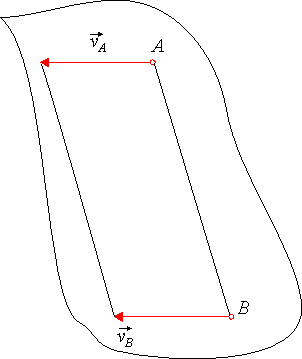
                                                               Rys 19.8                                                                              Rys 19.9

19.4. Prędkość bryły w ruchu płaskim

19.4.1 Rozkład prędkości w ruchu płaskim
    Rozpatrzymy ruch płaski bryły jako złożony z postępowego ruchu unoszenia i z obrotowego ruchu względnego (patrz p. 19.1). Prędkość dowolnego punktu figury płaskiej, na przykład punktu A (rys. 19.10a), jest wówczas równa sumie geometrycznej prędkości unoszenia dowolnego punktu przyjętego za biegun, na przykład punktu O oraz prędkości względnej punktu A względem punktu O.

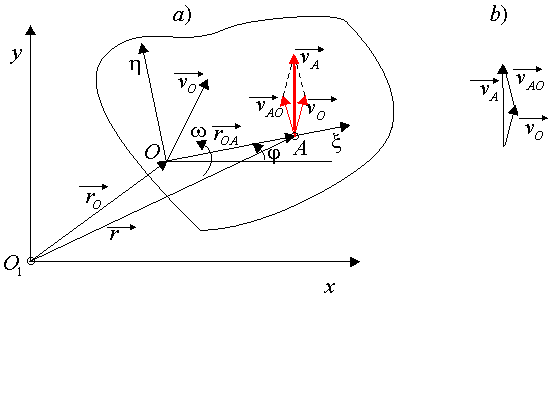
Rys 19.10

Prędkość ta jest równa

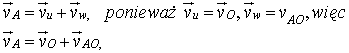                                                                                                                               (19.6)               

Wartość prędkości  wynosi

                                                                                                                                                                                                 (19.7)                                                                                                                                                                                                                                                               
Na (rys19.1b) pokazano wykres wektorowy, przedstawiający prędkość punktu A.

19.4.2 Analityczne wyznaczenie prędkości

 Dla przykładu położenie dowolnego punktu np. A  figury płaskiej (rys. 19.10) określono wektorem-promieniem wodzącym:

Różniczkując powyższe równanie względem czasu t, otrzymujemy:

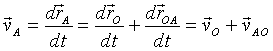,                                                                                                                                                  (19.8)          
gdzie jest prędkością punktu O, a przedstawia prędkość liniową punktu A względem bieguna O. Ponieważ zgodnie z równaniem (19.3):,
więc

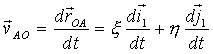                                                                                                                                                               (19.9)
Na podstawie wzorów Poissona jest:

zatem

,                                                                                                                                                                                                                      (19.10)
stąd ostatecznie

                                                                                                                                                                                         (19.11)                   Prędkość jest prostopadła do OA i skierowana w stronę obrotu figury płaskiej.
Wartość jej wyznaczamy ze wzoru (19.7).
Całkowita prędkość  punktu A jest równa:

                                                                                                                                                              (19.12)           

Rzutując równanie (19.12) na nieruchomy układ współrzędnych O_xy, otrzymujemy:

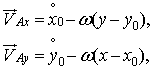                                                                                                                                                                             (19.13)                                                                                                                                                                                                                             
gdzie v_Ax, v_Ay, są rzutami prędkości punktu A na osie - rzutami  prędkości punktu O na osie O_x, O_y,   a jest rzutem prędkości kątowej na oś prostopadłą do płaszczyzny kierowniczej.
Rzuty prędkości punktu A na osie ruchomego układu współrzędnych wynoszą:

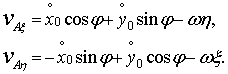                                                                                                                                                          (19.14)                  Wartość i kierunek prędkości punktu A wyznaczamy ze wzorów:

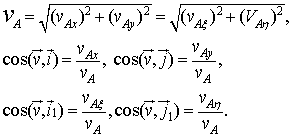                                                                                                                                                                                                         (19.15)/(19.16)      

19.5. Centroidy

Ruch płaski można rozpatrywać jako szereg po sobie następujących obrotów chwilowych figury płaskiej wokół  coraz to nowego punktu należącego do układu ruchomego (chwilowego) środka obrotu i zajmującego  w danej chwili określone położenia w układzie nieruchomym. W układzie ruchomym można wyróżnić wszystkie te punkty figury płaskiej, które były lub będą chwilowymi środkami obrotu. Punkty te w układzie ruchomym tworzą pewną krzywą, zwaną centroidą ruchomą.

Centroida ruchoma jest to miejsce geometryczne chwilowych środków obrotu figury płaskiej w układzie ruchomym.

Analogicznie w układzie nieruchomym można wyróżnić wszystkie punkty, które pokrywały się lub będą się pokrywać z chwilowym środkiem obrotu. Punkty te w układzie nieruchomym tworzą pewną krzywą, zwaną centroidą nieruchomą. 

Centroida nieruchoma jest to miejsce geometryczne chwilowych środków obrotu w układzie nieruchomym.

 Ruch płaski można uważać jak ruch zrealizowany przez toczenie się bez poślizgu centroidy ruchomej po centroidzie nieruchomej. Ponieważ prędkość chwilowego środka obrotu jest równa zero, więc korzystając ze wzoru (19.13) otrzymujemy równanie położenia chwilowego środka obrotu w postaci:

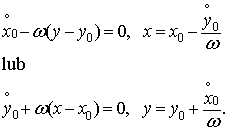                                                                                                                                                                                                                         (19.17)
Korzystając ze wzoru (19.14), otrzymamy równanie położenia chwilowego środka obrotu w układzie ruchomym postaci:

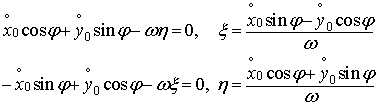                                                                                                                          (19.18)                                                                                  
Rugując czas t ze wzoru (19.17) i (19.18), otrzymujemy równanie centroidy nieruchomej i centroidy ruchomej.

 19.6 Przyspieszenia punktów bryły w ruchu płaskim

19.6.1 Rozkład przyspieszeń w ruchu płaskim

Rozpatrzymy ruchu płaski bryły jako złożony z postępowego ruchu unoszenia i obrotowego ruchu względnego (patrz p. 19.1).

Przyspieszenie dowolnego punktu figury płaskiej, na przykład punktu A (rys. 19.11a), jest równe sumie geometrycznej przyspieszenia unoszenia dowolnego punktu przyjętego za biegun, na przykład punktu O, oraz przyspieszenia względnego punktu A wokół bieguna O.

Przyspieszenie to jest równe
Ponieważ

  więc 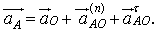                                               (19.19)                                                                                                                    

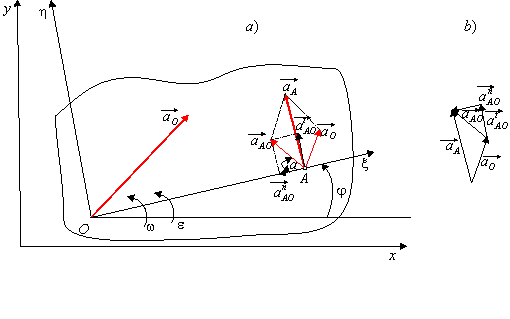
Rys 19.11

Wartości przyspieszeń wynoszą:

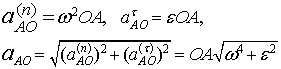                                                                                                                             (19.20)/(19.21)                                                                     

gdzie jest wartością prędkości kątowej ruchu względnego, a    -  wartością przyspieszenia kątowego ruchu względnego.

Na (rys 19.11b) pokazano wykres wektorowy równania (19.19).
Jeżeli zmienimy  położenie punktu A (weźmiemy pod uwagę inny punkt bryły), to dalej nie ulega zmianie, zmienia się natomiast

Przyspieszenie a=a_AO tworzy z odcinkiem OA kąt (rys. 19.11a), który jest w danej chwili taki sam dla wszystkich punktów bryły, nie zależy więc od położenia punktu A.

                                                                                                                                                                                                               (19.22)           

19.6.2 Analityczne wyznaczenie przyspieszeń

Prędkość punktu A zgodnie ze wzorem (19.12)  jest równa

Różniczkując powyższe równanie względem czasu t, otrzymamy przyspieszenie punktu A (rys. 19.3a)

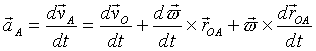                                                                                                                                  (19.23)

Ponieważ

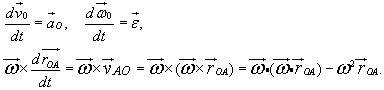
Ale

czyli ostatecznie przyspieszenie aA punktu A jest równe:

                                                                                                                                                             (19.24)                                                                                                                                                                                                                                                            Rzutując równanie (19.24) na osie nieruchomego układu współrzędnych O_xy, otrzymujemy:

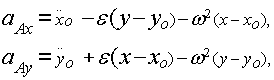                                                                                                                                                                                                                   (19.25)                         

gdzie a_Ax, a_Ay są rzutami przyspieszenia punktu A na osie - rzutami przyspieszenia punktu O na osie  - rzutami prędkości kątowej i przyspieszenia kątowego na oś prostopadłą do płaszczyzny kierowniczej.
Rzuty przyspieszenia punktu A na osie ruchomego układy współrzędnych   są równe

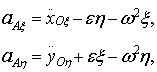.                                                                                                                                                                              (19.26)

Wartość i kierunek przyspieszenia punktu A wyznaczamy ze wzorów:

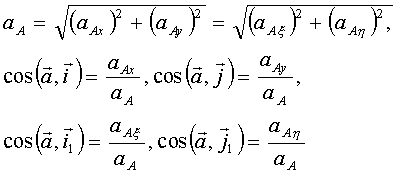                                                                                                                    (19.27)   
  
Przykład 19.1

Mechanizm prętowy połączony przegubowo jak na (rys 19.12) składa się z czterech prętów, przy czym pręty (korby) O₁A i O₂B obracają się w kierunkach zaznaczonych na (rys 19.12). W rozpatrywanej chwili pręt O₁A jest pionowy, pręty AC i O₂B poziome, a pręt BC tworzy z pionem kąt 30⁰.

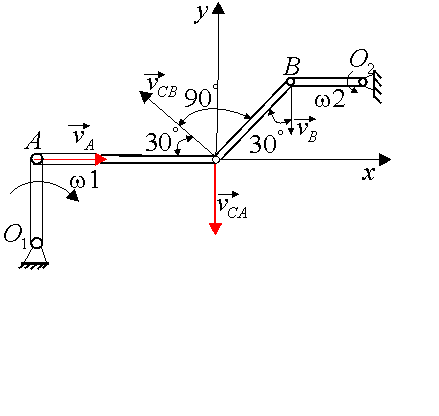
Rys. 19.12

Mając dane: wyznaczyć wartość prędkości punktu C.

Rozwiązanie:

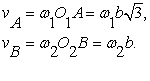
Zwroty wektorów pokazano na rysunku. Punkt C należy równocześnie do członu AC i BC. Korzystając ze wzoru (19.6) znajdujemy z jednej strony

                                                                                                                                                                                   (a)                                                                                                                                                                                                                                                                z drugiej

                                                                                                                                                                                    (b)                                                                                                                                                                                                                                                              Porównując prawe strony (a) i (b), otrzymujemy:
                                                                                                                                                               (c)
Wektory         jednak zwroty i ich wartości są nieznane. Przyjmujemy umownie, że wektory te mają zwroty takie jak na rysunku. Prowadzimy osie współrzędnych prostokątnych i rzutujemy na nie równanie  (c). Otrzymujemy dwa równania:

Z pierwszego z równań znajdujemy:

Znak minus wskazuje na to, że wektor w rzeczywistości ma zwrot przeciwny do przyjętego.
Z drugiego równania otrzymujemy:

Ponieważ więc zgodnie z (a)

 
Przykład 19.2

 Wyznaczyć prędkość końca A pręta AB o długości l, jeżeli jego końce ślizgają się po dwóch wzajemnie prostopadłych prowadnicach, a prędkość końca jest stała i równa V_B ( rys 19.13 ).

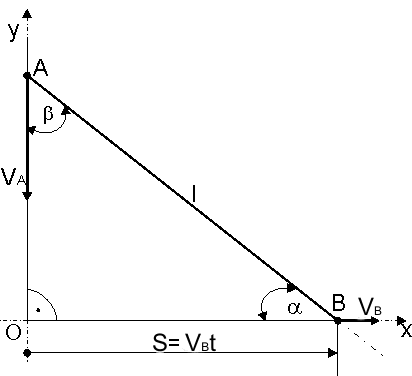
Rys. 19.13

Rozwiązanie:

Prędkość V_A końca A pręta jest styczna do toru, a więc pionowa, skierowana do dołu. Rzut tej prędkości na kierunek AB wynosi

i zgodnie ze wzorem    jest równy rzutowi prędkości V_B punktu B na prostą AB, a zatem

gdzie

 
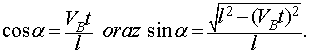
Przykład 19.3

Oś walca, który toczy się bez poślizgu po równi pochyłej (rys. 19.14), przemieszcza się według równania s=4t²+16 ( t  wyrażono w sekundach a  s - w metrach ). Wyznaczyć przyspieszenie punktu walca stykającego się z równią w chwili t=2, jeżeli promień walca R=16 cm.

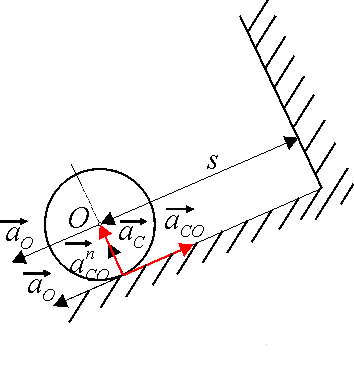
Rys. 19.14

Rozwiązanie:

Wartości prędkości i przyspieszenia punktu O leżących na osi jest równa 

Dla t=2s, V₀ = 16cm/s, a a₀= 8cm/s²

Chwilowy środek prędkości jest w punkcie styku walca z równią, a zatem

Różniczkując powyższe równanie względem czasu, otrzymujemy

Wyznaczamy przyspieszenie punktu C. Zgodnie ze wzorem (19.19)

gdzie dla t=2s

przy czym ma zwrot od C do O, a jest prostopadłe do CO o zwrocie w stronę figury wokół bieguna O. W rozpatrywanym przypadku

a więc , a ostatecznie a_c=16cm/s

Pytania i ćwiczenia sprawdzające
    1. Jaki ruch ciała nazywamy płaskim?
    2. Wzór na prędkość punktu ciała w ruchu płaskim (omówić).
    3. Co to jest chwilowy środek obrotu?
    4. Podać sposoby wyznaczania chwilowego środka obrotu.
    5. Wzór na przyspieszenie punktu ciała w ruchu płaskim (omówić).     

Ćwiczenia

Na krążek 1 o promieniu R i masie m₁ mogący obracać się wokół poziomej gładkiej osi została nawinięta nić, której drugi koniec nawinięto na krążek 2, o masie m₂ i promieniu r. Krążek 2 opada pod działaniem siły ciężkości. Obliczyć przyspieszenie a_c środka krążka. (Rys19.22)

Odpowiedź:

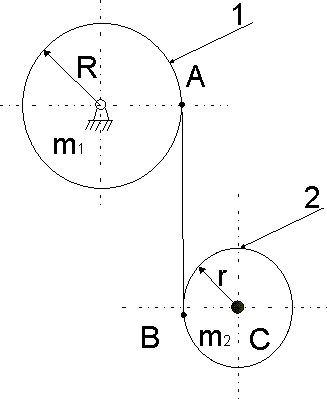
Rys. 19.22

Dla mechanizmu korbowego jak na (Rys 19.23) obliczyć prędkości i przyspieszenie suwaka B. Korba OB obraca się ze stałą prędkością kątową . Pozostałe dane są następujące: OB=r[m], BA=l[m], .

Odpowiedź:

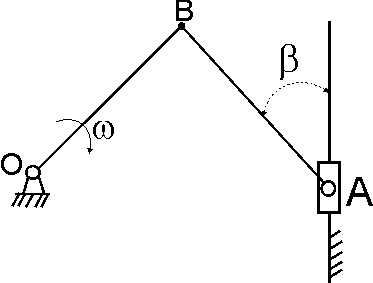
Rys. 19.23