Temat:21 Ruch drgający punktu materialnego
21.1 Drgania swobodne nietłumione
Ruchem drgającym punktu materialnego
(drganiem) nazywamy ruch w dostatecznie małym
otoczeniu położenia swojej równowagi stałej tego punktu. Jeżeli
punkt materialny zostanie wychylony z położenia równowagi, to zostaną
wywołane drgania tego punktu.
W wielu zagadnieniach
mamy do czynienia z ruchem punktu materialnego,
na który działa siła ![]() proporcjonalna
do tego wychylenia od pewnego nieruchomego
punktu
proporcjonalna
do tego wychylenia od pewnego nieruchomego
punktu ![]() i skierowana
w stronę tego punktu. Rozpatrzymy przypadek, gdy punkt materialny
porusza się po linii prostej, na której leży
również wspomniany wyżej punkt
i skierowana
w stronę tego punktu. Rozpatrzymy przypadek, gdy punkt materialny
porusza się po linii prostej, na której leży
również wspomniany wyżej punkt ![]() . Jeżeli tę prostą obierzemy
jako oś
. Jeżeli tę prostą obierzemy
jako oś ![]() z początkiem
w punkcie
z początkiem
w punkcie ![]() (rys.
21.1), a współczynnik proporcjonalności
między siłą przyciągającą a wychyleniem punktu materialnego oznaczmy
symbolem
(rys.
21.1), a współczynnik proporcjonalności
między siłą przyciągającą a wychyleniem punktu materialnego oznaczmy
symbolem ![]() , to równanie różniczkowe ruchu
będzie miało postać:
, to równanie różniczkowe ruchu
będzie miało postać:
![]()

Znak minus po prawej stronie powyższego
równania pochodzi stąd, iż dla ![]() siła
siła ![]() ma zwrot
przeciwny do osi
ma zwrot
przeciwny do osi ![]() , a dla
, a dla ![]() siła ta ma zwrot zgodny z osią. Przenosząc w równaniu tym wyraz
siła ta ma zwrot zgodny z osią. Przenosząc w równaniu tym wyraz
![]() na lewą stronę
mamy:
na lewą stronę
mamy:
![]() (21.1)
(21.1)
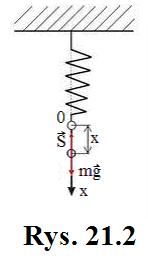
Z równaniem tego typu spotkamy się na
przykład przy badaniu małych pionowych ruchów ciała zawieszonego
na sprężynie (rys.21.2) .
Na ciało działają
następujące siły: siła ciężkości ![]() oraz reakcja sprężyny
oraz reakcja sprężyny ![]() . Ponieważ dla małych odkształceń
zachodzi proporcjonalność między siłą rozciągającą
sprężynę i jej wydłużeniem, przeto oznaczając symbolem
. Ponieważ dla małych odkształceń
zachodzi proporcjonalność między siłą rozciągającą
sprężynę i jej wydłużeniem, przeto oznaczając symbolem ![]() mierzone
pionowo w dół wychylenie ciała z położenia równowagi, a
mierzone
pionowo w dół wychylenie ciała z położenia równowagi, a
symbolem ![]() wydłużenie statyczne sprężyny otrzymujemy:
wydłużenie statyczne sprężyny otrzymujemy:
![]()
![]()
przy czym
![]() oznacza teraz
tak zwany współczynnik sprężystości sprężyny. Biorąc pod uwagę,
że w rozpatrywanym przypadku
oznacza teraz
tak zwany współczynnik sprężystości sprężyny. Biorąc pod uwagę,
że w rozpatrywanym przypadku
![]() , otrzymujemy
następujące równanie ruchu:
, otrzymujemy
następujące równanie ruchu:
![]()
![]() (21.2)
(21.2)
Ponieważ ![]() jest wydłużeniem statycznym sprężyny,
czyli wydłużeniem w położeniu równowagi, w którym siła ciężkości
zawieszonego ciała równoważy się z reakcją sprężyny
, przeto:
jest wydłużeniem statycznym sprężyny,
czyli wydłużeniem w położeniu równowagi, w którym siła ciężkości
zawieszonego ciała równoważy się z reakcją sprężyny
, przeto:
![]()
![]()
a stąd
![]()
Podstawiając w równaniu (21.2) powyższą zależność, otrzymujemy równanie ruchu identyczne z (21.1) . Po podzieleniu równania (21.1) przez masę m otrzymamy:
![]() ,
(21.3)
,
(21.3)
przy czym
![]() ,
, ![]() (21.4)
(21.4)
Rozwiązanie ogólne równania (21.3) jest następujące:
![]() (21.5)
(21.5)
albo po przekształceniu
![]() (21.6)
(21.6)
![]() ,
, ![]()
![]()
![]() (21.7)
(21.7)
Z równania (21.6) wynika, że rozpatrywany punkt materialny porusza się
ruchem harmonicznym prostym, przy czym częstość drgań równa
jest parametrowi ![]() określonemu
wzorem (21.4), a
okres drgań wynosi:
określonemu
wzorem (21.4), a
okres drgań wynosi:
![]() (21.8)
(21.8)
Stałe całkowania ![]() i
i ![]() wyznaczamy
z warunków początkowych. Jeżeli w chwili
wyznaczamy
z warunków początkowych. Jeżeli w chwili
![]() wychylenie punktu materialnego z
położenia
wychylenie punktu materialnego z
położenia
równowagi
wynosiło ![]() , a wartość prędkości wynosiła
, a wartość prędkości wynosiła
![]() , to
, to
![]() ,
,
![]()
a więc
![]() (21.9)
(21.9)
gdy ![]() , wtedy
, wtedy
![]()
Wielkość ![]() nazywa się częstością drgań własnych
punktu materialnego o masie
nazywa się częstością drgań własnych
punktu materialnego o masie ![]() . Wielkość
. Wielkość
![]() określającą
maksymalne wychylenie punktu z położenia równowagi nazwano amplitudą
drgań. W tym przypadku amplituda drgań jest równa
wychyleniu początkowemu z położenia równowagi.
określającą
maksymalne wychylenie punktu z położenia równowagi nazwano amplitudą
drgań. W tym przypadku amplituda drgań jest równa
wychyleniu początkowemu z położenia równowagi.
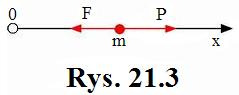
Załóżmy, że oprócz siły ![]() , proporcjonalnej do wychylenia,
na punkt materialny działa jeszcze pewna siła
, proporcjonalnej do wychylenia,
na punkt materialny działa jeszcze pewna siła ![]() , której wartość jest okresową funkcją
czasu (rys.21.3),
przy czym:
, której wartość jest okresową funkcją
czasu (rys.21.3),
przy czym:
![]()
 Równanie różniczkowe ruchu przybierze teraz postać:
Równanie różniczkowe ruchu przybierze teraz postać:
![]()
albo
![]() ,
(21.10)
,
(21.10)
przy czym, jak poprzednio,
![]() .
.
Równanie (21.10) jest równaniem różniczkowym liniowym niejednorodnym.
Jego rozwiązanie ogólne równe jest sumie rozwiązania ogólnego odpowiedniego
równania jednorodnego, a więc w danym przypadku równania (21.3),
oraz rozwiązania szczególnego.
Oznaczmy pierwsze z tych rozwiązań symbolem ![]() , drugie zaś, tj.
rozwiązanie szczególne równania (21.10),
symbolem
, drugie zaś, tj.
rozwiązanie szczególne równania (21.10),
symbolem ![]() . Otrzymamy wówczas:
. Otrzymamy wówczas:
![]() (21.11)
(21.11)
przy czym zgodnie z (21.5)
.
![]() (21.12)
(21.12)
Rozwiązaniem szczególnego równania (21.10) szukamy w postaci:
![]() (21.13)
(21.13)
gdzie ![]() jest stałym
współczynnikiem, którego wartość należy wyznaczyć. Podstawiając w
(21.10) wyrażenie (21.13), otrzymujemy:
jest stałym
współczynnikiem, którego wartość należy wyznaczyć. Podstawiając w
(21.10) wyrażenie (21.13), otrzymujemy:
![]()
Aby powyższe równanie było tożsamościowo spełnione, powinno być:
![]()
czyli
![]() (21.14)
(21.14)
Poszukiwanym rozwiązaniem szczególnym jest więc
![]() (21.15)
(21.15)
Uwzględniając zależności (21.11) i (21.12), otrzymujemy:
![]() (21.16)
(21.16)
Na podstawie (21.16) stwierdzamy, że ruch punktu materialnego stanowi wynik superpozycji dwóch rodzajów drgań harmonicznych. Pierwsze z nich pokrywają się z badanymi poprzednio drganiami swobodnymi, drugie zaś odpowiadają szczególnemu rozwiązaniu (21.14). Te ostatnie drgania noszą nazwę drgań wymuszonych, a ich okres
![]() (21.17)
(21.17)
jest taki sam jak okres siły ![]() wywołującej tedrgania.
Zgodnie z równaniami (21.14) i (21.4) amplituda
drgań wymuszonych wynosi
wywołującej tedrgania.
Zgodnie z równaniami (21.14) i (21.4) amplituda
drgań wymuszonych wynosi
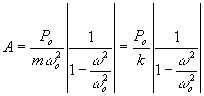 (21.18)
(21.18)
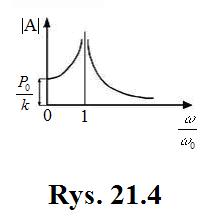
Wartość amplitudy ![]() zależy od
stosunku
zależy od
stosunku ![]() , czyli od stosunku częstości siły
, czyli od stosunku częstości siły
![]() do częstości
drgań swobodnych. Na rysunku (21.4)
zależność tę przedstawiono wykreślnie.
do częstości
drgań swobodnych. Na rysunku (21.4)
zależność tę przedstawiono wykreślnie.
Gdy ![]() = 0, czyli gdy
siła wymuszająca jest stała, wtedy
= 0, czyli gdy
siła wymuszająca jest stała, wtedy ![]() i z równania
(21.16) wynika, że punkt materialny wykonuje
drgania swobodne, których środkiem jest położenie
równowagi określone odciętą
i z równania
(21.16) wynika, że punkt materialny wykonuje
drgania swobodne, których środkiem jest położenie
równowagi określone odciętą ![]() . Gdy
. Gdy ![]() a amplituda drgań wymuszonych
dąży do
a amplituda drgań wymuszonych
dąży do
zera i wreszcie gdy ![]() , to znaczy gdy częstość siły wymuszającej
zbliża się do częstości drgań własnych, amplituda drgań wymuszonych
wzrasta nieorganicznie. Przypadek
, to znaczy gdy częstość siły wymuszającej
zbliża się do częstości drgań własnych, amplituda drgań wymuszonych
wzrasta nieorganicznie. Przypadek ![]() wyłączamy na razie z naszych rozważań , gdyż wówczas rozwiązanie szczególne (21.15)
traci sens. Przypadkiem tym, który nosi
nazwę rezonansu, zajmiemy się osobno. Rozwiązanie
(21.15) odpowiadające drganiom
wymuszonym możemy przedstawić w następującej postaci:
wyłączamy na razie z naszych rozważań , gdyż wówczas rozwiązanie szczególne (21.15)
traci sens. Przypadkiem tym, który nosi
nazwę rezonansu, zajmiemy się osobno. Rozwiązanie
(21.15) odpowiadające drganiom
wymuszonym możemy przedstawić w następującej postaci:
gdy: ![]()
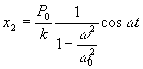
gdy: ![]()
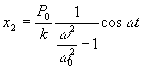
Z powyższego wynika, że częstość siły
wymuszającej ![]() jest mniejsza
od częstości drgań własnych, drgania wymuszone mają taki gdy sam
kąt przesunięcia fazowego jak wspomniana wyżej
siła. Natomiast gdy siła
jest mniejsza
od częstości drgań własnych, drgania wymuszone mają taki gdy sam
kąt przesunięcia fazowego jak wspomniana wyżej
siła. Natomiast gdy siła ![]() ma częstość
większą od częstości drgań własnych, wówczas drgania wymuszone są
spóźnione w fazie o pół okresu.
ma częstość
większą od częstości drgań własnych, wówczas drgania wymuszone są
spóźnione w fazie o pół okresu.
Zajmiemy się teraz zbadaniem przypadku,
gdy ![]() , a więc przypadkiem
rezonansu. Równanie różniczkowe ruchu przyjmie postać:
, a więc przypadkiem
rezonansu. Równanie różniczkowe ruchu przyjmie postać:
![]() (21.19)
(21.19)
Rozwiązanie szczególne tego równania jest następujące:
![]()
Ponieważ
![]() ,
,
przeto, aby rozwiązanie szczególne miało przyjętą wyżej postać, powinno być
![]()
czyli
![]() .
.
Otrzymujemy więc ostatecznie:
![]() (21.20)
(21.20)
Drgania wymuszone nie są już teraz drganiami
harmonicznymi, można natomiast je traktować jako drgania okresowe
o amplitudzie rosnącej proporcjonalnie do czasu ![]() . Są one przy tym opóźnione w stosunku
do siły
. Są one przy tym opóźnione w stosunku
do siły ![]() o ćwierć
okresu. Na (rys. 21.5) podano wykres przedstawiający przebieg
drgań wymuszonych .
o ćwierć
okresu. Na (rys. 21.5) podano wykres przedstawiający przebieg
drgań wymuszonych .
W rozwiązaniu ogólnym (21.16),
ważnym dla przypadku, gdy ![]() , występują dwie stałe dowolne,
które należy wyznaczyć z warunków początkowych ruchu. Przyjmiemy,
że dla
, występują dwie stałe dowolne,
które należy wyznaczyć z warunków początkowych ruchu. Przyjmiemy,
że dla ![]() mamy
mamy ![]() i
i ![]() . Po prostych rachunkach
otrzymamy:
. Po prostych rachunkach
otrzymamy:
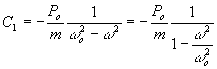
natomiast
![]()
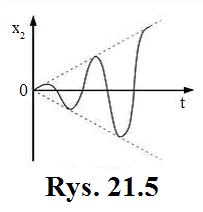
W
tym szczególnym przypadku równanie ruchu ma
więc postać: ![]()
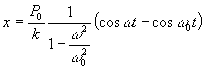 (21.21)
(21.21)
Załóżmy teraz, że częstość siły wymuszającej
różni się bardzo mało od częstości drgań własnych, czyli że rozpatrujemy
przypadek bliski rezonansu.
Wprowadzając oznaczenie
![]() ,
,
otrzymujemy:
![]()
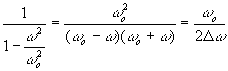
![]()
![]()
Uwzględniając powyższe przybliżone zależności równania (21.21) możemy nadać teraz postać:
![]() .
(21.22)
.
(21.22)
Traktując wyrażenie w nawiasie jako zmienną sinusoidalnie w czasie amplitudę, możemy drgania, które wykonuje punkt materialny, rozpatrywać jako drgania o okresie
![]() ,
,
a więc równym okresowi drgań własnych o zmiennej amplitudzie:
![]() .
(21.23)
.
(21.23)
Okres zmiany amplitudy
![]()
jest bardzo
duży w porównaniu z okresem ![]() ,gdyż z założenia
,gdyż z założenia ![]() jest małe.
Zależność
jest małe.
Zależność ![]() od czasu
od czasu ![]() wynikającą z
równania (21.22) pokazano na (rys.
21.6)
wynikającą z
równania (21.22) pokazano na (rys.
21.6)
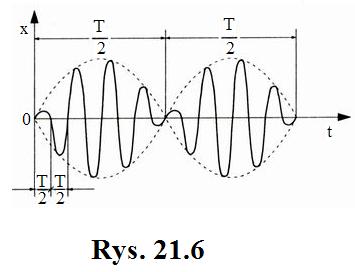
Jaka jest z rysunku, amplituda drgań na przemian to wzrasta, to maleje.Tego rodzaju zjawisko, które można zaobserwować w pobliżu rezonansu, nosi nazwę dudnienia.
21.3. Drgania swobodne tłumione
W poprzednich punktach przy rozpatrywaniu
małych drgań pominięto opory ruchu. Obecnie założymy, że na punkt
materialny działa, oprócz siły ![]() proporcjonalnej do wychylenia, jeszcze siła oporu
proporcjonalnej do wychylenia, jeszcze siła oporu
![]() , której wartość jest wprost proporcjonalna
do prędkości. Jak wynika z doświadczeń,
to ostatnie założenia daje zadowalające przybliżenie w przypadku
nieznacznych prędkości ruchu, z jakimi mamy do czynienia przy rozpatrywaniu
małych drgań sprężystych. Jeżeli oznaczamy symbolem
, której wartość jest wprost proporcjonalna
do prędkości. Jak wynika z doświadczeń,
to ostatnie założenia daje zadowalające przybliżenie w przypadku
nieznacznych prędkości ruchu, z jakimi mamy do czynienia przy rozpatrywaniu
małych drgań sprężystych. Jeżeli oznaczamy symbolem
 współczynnik
proporcjonalności między siłą
współczynnik
proporcjonalności między siłą ![]() i prędkością
i prędkością
![]() , to:
, to:
![]() (21.24)
(21.24)
i zgodnie z (rys. 21.7) równanie różniczkowe ruchu dla drgań swobodnych ma postać:
![]() (21.25)
(21.25)
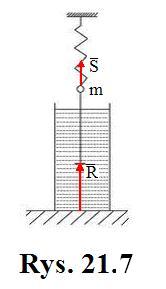
przy czym, jak poprzednio ![]() odpowiada
położeniu równowagi.
odpowiada
położeniu równowagi.
Wprowadzając oznaczenia
![]()
![]() ,
(21.26)
,
(21.26)
równanie (21.25) można napisać w postaci:
![]() (21.27)
(21.27)
Otrzymaliśmy jednorodne liniowe równanie różniczkowe, którego
równanie charakterystyczne
![]() (21.28)
(21.28)
ma następujące pierwiastki:
![]() ,
, ![]() .
(21.29) .
.
(21.29) .
Jeżeli założymy, że ![]() (przypadek
tzw. tłumienia podkrytycznego) , pierwiastki te są zespolone
i rozwiązanie ogólne równania
(przypadek
tzw. tłumienia podkrytycznego) , pierwiastki te są zespolone
i rozwiązanie ogólne równania
(21. 27) ma postać
![]()
![]() .
(21.30)
.
(21.30)
Z powyższego wynika , że punkt materialny
wykonuje drgania , których amplituda ![]() maleje,
tak jak pokazano na
maleje,
tak jak pokazano na
(rys.21.8). Jeżeli jako okres
tych drgań będziemy przyjmować odstęp czasu miedzy
kolejnymi chwilami, w których punkt
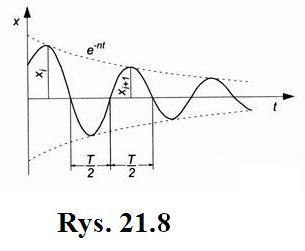
materialny przechodzi przez położenie równowagi ![]() z prędkościami o jednym kierunku,
to:
z prędkościami o jednym kierunku,
to:
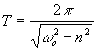 (21.31)
(21.31)
W przypadku, gdy
tłumienie jest małe, czyli gdy współczynnik ![]() jest znacznie
mniejszy od
jest znacznie
mniejszy od ![]() , okres drgań tłumionych różni się
tylko nieznacznie od okresu obliczonego wg wzoru (21.8) wyprowadzonego dla drgań bez tłumienia. Obliczamy
stosunek dwóch jakichkolwiek kolejnych maksymalnych (lub minimalnych)
wychyleń punktu materialnego. Ponieważ, jak łatwo wykazać, odstęp czasu między chwilami, w których
współrzędna
, okres drgań tłumionych różni się
tylko nieznacznie od okresu obliczonego wg wzoru (21.8) wyprowadzonego dla drgań bez tłumienia. Obliczamy
stosunek dwóch jakichkolwiek kolejnych maksymalnych (lub minimalnych)
wychyleń punktu materialnego. Ponieważ, jak łatwo wykazać, odstęp czasu między chwilami, w których
współrzędna ![]() osiąga maksimum , równy jest okresowi
osiąga maksimum , równy jest okresowi
![]() wynikającemu
ze wzoru (21.31), przeto:
wynikającemu
ze wzoru (21.31), przeto:
![]() .
.
Logarytm tego stosunku, czyli
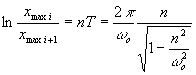 (21.32)
(21.32)
nosi nazwę
dekrementu tłumienia i jest miarą intensywności
tłumienia. Omówimy teraz nowy przypadek, gdy ![]() (przypadek tzw. tłumienia nadkrytycznego), pierwiastki równania charakterystycznego
(21.29) są rzeczywiste i oba ujemne,
rozwiązanie ogólne równania (21.28) ma
postać :
(przypadek tzw. tłumienia nadkrytycznego), pierwiastki równania charakterystycznego
(21.29) są rzeczywiste i oba ujemne,
rozwiązanie ogólne równania (21.28) ma
postać :
![]()
![]() (21.33)
(21.33)
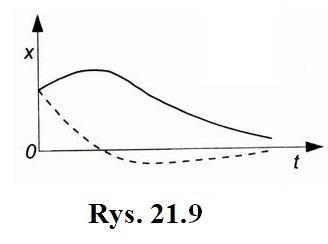
Charakter krzywych przedstawiających
zależność współrzędnej ![]() od
czasu
od
czasu ![]() pokazano
na (rys.21.9). Z rysunku tego wynika, że w rozpatrywanym przypadku
nie mamy już do czynienia z drganiami i wychylenie punktu maleje, bardzo
szybko zdążając asymptotycznie do zera.
pokazano
na (rys.21.9). Z rysunku tego wynika, że w rozpatrywanym przypadku
nie mamy już do czynienia z drganiami i wychylenie punktu maleje, bardzo
szybko zdążając asymptotycznie do zera.
Gdy wreszcie ![]() (przypadek tzw. tłumienia krytycznego) rozwiązanie równania
(21.28) ma postać:
(przypadek tzw. tłumienia krytycznego) rozwiązanie równania
(21.28) ma postać:
![]() (21.34)
(21.34)
I podobnie jak poprzednio nie występują drgania. We wszystkich trzech przypadkach
stałe ![]() i
i ![]() wyznacza
się z warunków początkowych.
wyznacza
się z warunków początkowych.
21.4. Drgania wymyszone tłumione
Zbadamy
teraz wpływ tłumienia
na drgania wymuszone. Jeżeli oprócz sił ![]() i
i ![]() na punkt
materialny działać będzie jeszcze siła
na punkt
materialny działać będzie jeszcze siła ![]() , której wartość jest okresową funkcją czasu, przy
czym
, której wartość jest okresową funkcją czasu, przy
czym ![]() , to równanie różniczkowe ruchu
ma postać :
, to równanie różniczkowe ruchu
ma postać :
![]() (21.35)
(21.35)
Albo, stosując oznaczenia (21.26), postać :
![]() (21.36)
(21.36)
Rozwiązanie tego równania równe jest sumie rozwiązania ogólnego
równania jednorodnego, które było podane poprzednio, oraz rozwiązania
szczególnego. To ostatnie będziemy poszukiwać w następującej postaci :
![]()
![]()
![]() (21.37)
(21.37)
Przy czym ![]() i
i ![]() oznaczają pewne stałe. Stałe te wyznaczamy z warunku,
aby równanie (21.36) było spełnione
tożsamościowo. Poszukiwane rozwiązanie szczególne
odpowiada drganiom wymuszonym w przypadku, gdy zachodzi tłumienie
tych drgań. Podstawiając w (21.36) zamiast
oznaczają pewne stałe. Stałe te wyznaczamy z warunku,
aby równanie (21.36) było spełnione
tożsamościowo. Poszukiwane rozwiązanie szczególne
odpowiada drganiom wymuszonym w przypadku, gdy zachodzi tłumienie
tych drgań. Podstawiając w (21.36) zamiast
![]() określone wzorem (21.37) i wykonując odpowiednie działanie, otrzymujemy:
określone wzorem (21.37) i wykonując odpowiednie działanie, otrzymujemy:
![]() ,
,
a stąd po przekształceniach
![]()
![]()
Aby więc równanie powyższe było spełnione tożsamościowo, powinno być :
![]() (21.38)
(21.38)
![]()
Z powyższych równań znajdujemy
![]() ,
, 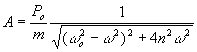 .
Dla rozstrzygnięcia, którą z dwóch
wartości kąta
.
Dla rozstrzygnięcia, którą z dwóch
wartości kąta ![]() w przedziale
od
w przedziale
od ![]() do
do ![]() należy przyjąć,
pomnóżmy pierwsze równanie układu (21.38) przez
należy przyjąć,
pomnóżmy pierwsze równanie układu (21.38) przez ![]() , drugie zaś przez
, drugie zaś przez ![]() i następnie
dodajmy je stronami. Otrzymamy wówczas :
i następnie
dodajmy je stronami. Otrzymamy wówczas :
![]() . (21.40)
. (21.40)
Jeżeli założymy, że ![]() , to z drugiego ze wzorów (21.39)
wyniknie, iż
, to z drugiego ze wzorów (21.39)
wyniknie, iż ![]() , a stąd na podstawie równania (21.40)
stwierdzamy ,
, a stąd na podstawie równania (21.40)
stwierdzamy ,
że
![]() , czyli
, czyli
![]() .
(21.41)
.
(21.41)
Rozwiązanie szczególne równania (21.36) ma ostatecznie postać:
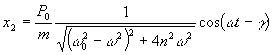 (21.42)
(21.42)
Ze wzoru na amplitudę drgań wymuszonych
wynika, że gdy ![]() , to znaczy, gdy występuje tłumienie,
pozostaje ona zawsze ograniczona, a w przypadku
, to znaczy, gdy występuje tłumienie,
pozostaje ona zawsze ograniczona, a w przypadku ![]() mamy :
mamy :
![]() .
(21.43)
.
(21.43)
Na podstawie drugiego równania (21.39) znajdujemy, że amplituda osiąga maksimum, gdy
![]() ,i wówczas
,i wówczas
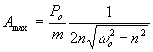 .
(21.44)
.
(21.44)
Jeżeli tłumienie jest małe, maksimum
amplitudy zachodzi dla ![]() bardzo bliskiego
bardzo bliskiego
![]() , jeżeli natomiast
, jeżeli natomiast ![]() , to amplituda osiąga
, to amplituda osiąga
ekstremum tylko dla ![]() i maleje
wraz z częstością
i maleje
wraz z częstością ![]() . W tym ostatnim
przypadku nie występuje zjawisko rezonansu polegające na znacznym
wzroście amplitudy drgań wymuszonych w okolicy
. W tym ostatnim
przypadku nie występuje zjawisko rezonansu polegające na znacznym
wzroście amplitudy drgań wymuszonych w okolicy ![]() .Na (rys
21.10) podano krzywe zależności amplitudy drgań wymuszonych
od stosunku
.Na (rys
21.10) podano krzywe zależności amplitudy drgań wymuszonych
od stosunku ![]() . Krzywe te wykreślono dla szczególnych
wartości parametru
. Krzywe te wykreślono dla szczególnych
wartości parametru ![]() , określającego intensywność
tłumienia.
, określającego intensywność
tłumienia.

Kąt ![]() , czyli kąt opóźnienia w fazie drgań wymuszonych w stosunku do okresowo
zmiennej siły
, czyli kąt opóźnienia w fazie drgań wymuszonych w stosunku do okresowo
zmiennej siły ![]() wywołującej
drgania , zależy
wywołującej
drgania , zależy
również od częstości ![]() , tej siły. Z pierwszego ze wzorów (21.39) wynika, że gdy
, tej siły. Z pierwszego ze wzorów (21.39) wynika, że gdy ![]() , wtedy
, wtedy ![]() , gdy
, gdy ![]() , wówczas kąt
, wówczas kąt
![]() .Gdy
.Gdy ![]() , kąt
, kąt ![]() co oznacza, że w tym przypadku,
tak jak dla drgań nietłumionych , drgania wymuszone są opóźnione w fazie o ćwierć okresu. Krzywe przedstawione na (rys.
21.11) podają zależność kąta
co oznacza, że w tym przypadku,
tak jak dla drgań nietłumionych , drgania wymuszone są opóźnione w fazie o ćwierć okresu. Krzywe przedstawione na (rys.
21.11) podają zależność kąta ![]() od stosunku
od stosunku ![]() . Krzywe te zostały wykreślone dla kilku szczególnych wartości parametru
. Krzywe te zostały wykreślone dla kilku szczególnych wartości parametru ![]() .
.


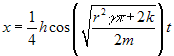


 (d)
(d)