23.1.Siły działające na punkt układu mechanicznego.

Układ punktów materialnych lub układ mechaniczny jest to zbiór punktów materialnych, w których położenie każdego punktu jest zależne od położeń innych punktów.  W układzie punktów materialnych punkty oddziaływują na siebie siłami według III prawa Newtona.

Układ punktów materialnych, których ruch nie jest ograniczony żadnymi więzami, nazywa się układem punktów swobodnych. Przykładem układu punktów swobodnych jest układ słoneczny, w którym planety rozpatruje się w astronomii jako punkty materialne. Planety przemieszczają się swobodnie po orbitach, zależnych od działających na planety sił.

Układ punktów materialnych, których ruch jest ograniczony nałożonymi na te punkty więzami, nazywa się układem punktów nieswobodnych.

Przykładem takiego układu może być dowolny mechanizm lub maszyna, w których ruch oddzielnych elementów jest ograniczony więzami.

Siły działające na punkty układu dzielą się na wewnętrzne i zewnętrzne.

Siły wewnętrzne są to siły, które pochodzą od wzajemnego oddziaływania punktów układu na siebie. O tych siłach założono, że stosują się do III prawa Newtona.
Siłami zewnętrznymi nazwano wszystkie pozostałe siły.      

Ruch punktów układu zależy zarówno od sił zewnętrznych, jak i od wewnętrznych. Na podstawie III prawa Newtona można stwierdzić, że:
1. Suma geometryczna wszystkich sił wewnętrznych układu  i suma ich rzutów na osie układu współrzędnych są równe zeru.   

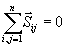                                                                                                                                             (23.1)

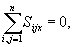
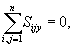
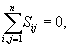
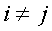                                                                                                   (23.2)
2. Momenty sił wewnętrznych układu względem dowolnego bieguna i względem osi układu współrzędnych są równe zeru.

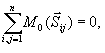                                                                                                           (23.3)

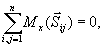
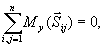
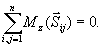                                                                                           (23.4)
Chociaż równania (23.2) i (23.4) mają postać równań równowagi sił, dowolnie położonych w przestrzeni, to siły wewnętrzne nie równoważą się i przyłożone do różnych punktów układu mogą wywołać przemieszczenie punktów względem siebie. Na przykład dwa naboje elektryczne przyciągają się lub odpychają..

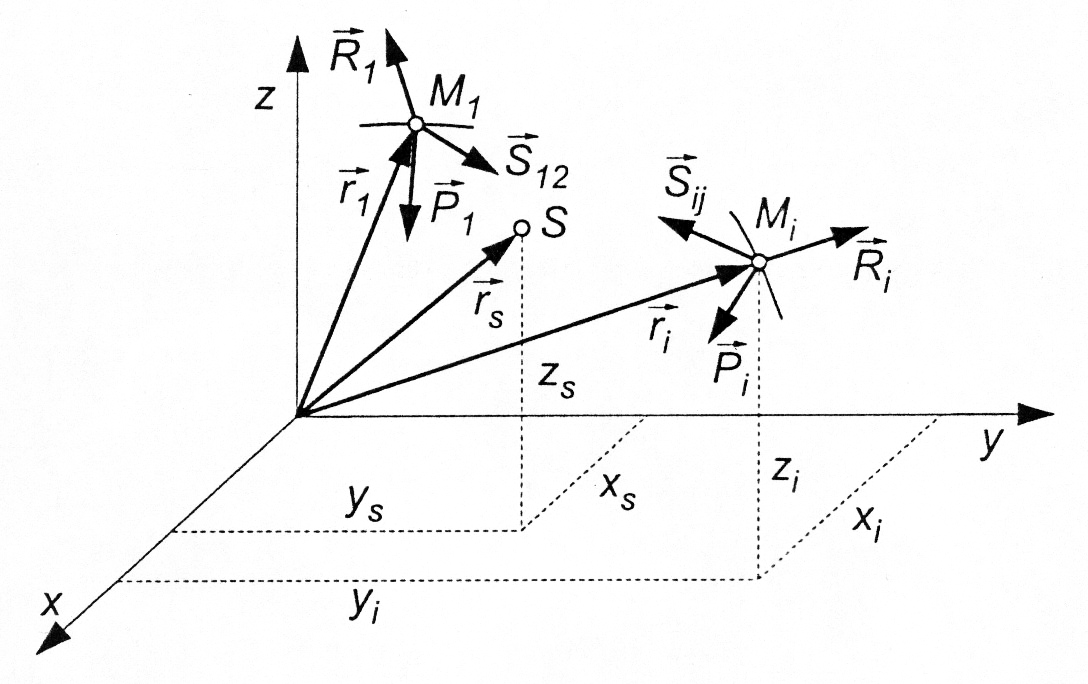
    Każdy punkt  M_i  układu mechanicznego ma określoną skończoną masę  m_i  i jego poło­żenie w układzie współrzędnych Oxyz w każdej chwili określa promień-wektor 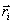 lub trzy współrzędne x_i, y_i, z_i (rys. 23.1).

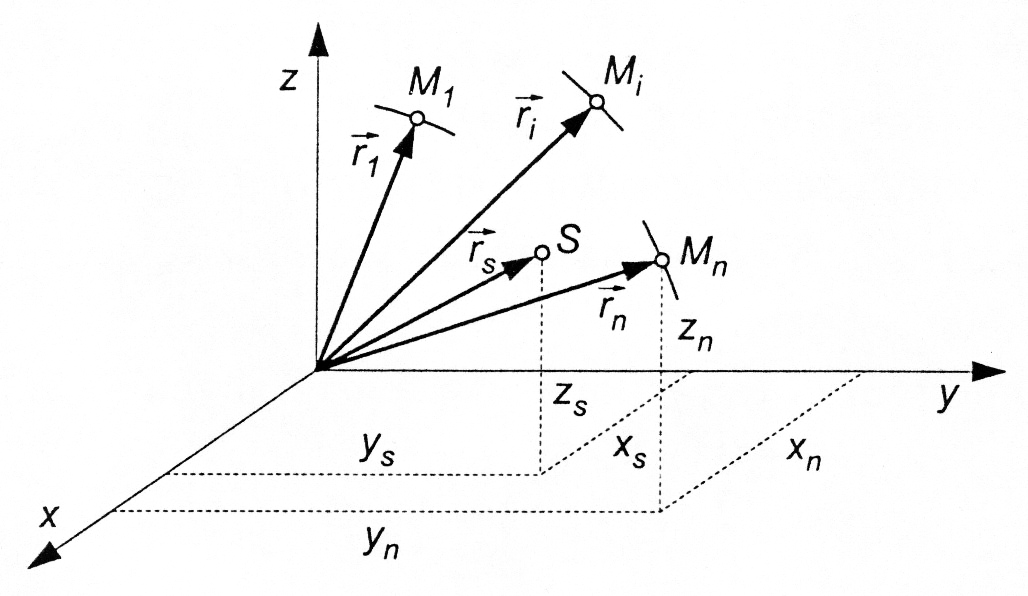
Rys. 23.1

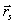Środkiem masy układu nazywa się punkt geometryczny S, którego promień-wektor  wyznacza się wg. wzoru: 

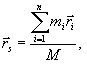                                                                                                                                                 (23.5)

gdzie 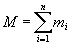 jest masą układu. 

Rzutując równania (23.5) na osie Ox, Oy, Oz, otrzymujemy:

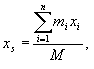
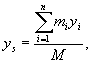
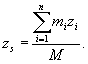                                                                                                       (23.6)

 23.3.Zasada ruchu środka masy.

         Przyjmijmy, że poruszający się układ punktów materialnych M₁, M₂, ..., M_n będzie pod działa­niem sił zewnętrznych i wewnętrznych (rys. 23.2). Masę każdego punktu oznaczono symbolem m_i.

Rys. 23.2

Równanie ruchu dla i-tego punktu układu ma postać:

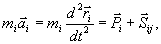
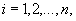                                                                                                                                                     (23.7)

gdzie 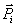 są siłami zewnętrznymi (czynne i reakcje), 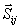 - siłami wewnętrznymi, 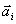 jest przyspieszeniem.

              
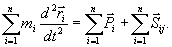                                                                                                                          (23.8)

Przekształcając lewą stronę równania (23.8) i korzystając ze wzoru (23.5), otrzymu­jemy:

                                                               
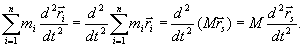
Suma geometryczna sił wewnętrznych jest równa zeru:
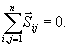
Oznaczając 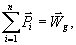  otrzymujemy równanie (23.8) w postaci:

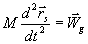                                                                                                                                                          (23.9)

  lub

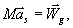                                                                                                                                             (23.10)

  albo w postaci:

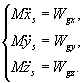                                                                                                                                                               (23.11)
Równanie (23.10) określa ruch środka masy. Z tego równania wynika, że siły we­wnętrzne nie mają wpływu na ruch środka masy. Równanie środka masy wypowiada się w formie zasady ruchu środka masy.
        Zasada ruchu środka masy.
Środek masy porusza się jak swobodny punkt mate­rialny o masie równej masie całego układu pod działaniem sumy geometrycznej sił czynnych i reakcji.
    Jeżeli suma geometryczna 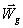 jest równa zeru, to 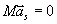. Z tego wynika, że 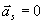, czyli prędkość  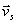jest stała lub równa zeru.
        Zasada zachowania ruchu środka masy.
Jeżeli suma geometryczna sił czynnych i reakcji jest równa zeru, to środek masy pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym (jeżeli miał początkową prędkość).

                                                                                                                                              (23.12)

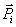gdzie  są siłami zewnętrznymi (czynne i reakcje), a 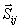- siłami wewnętrznymi.
   Przenosząc wszystkie wyrazy na jedną stronę, to równanie (23.12) przyjmie prostszą postać. Otrzymamy wówczas:

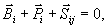                                                                                                                                             (23.13)

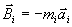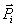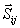gdzie wektor  traktujemy jako pomyślaną, fikcyjną siłę. Powyższe równanie można traktować jako równanie sił rzeczywistych działających na punkt m_i, tj. sił  i , oraz wspomnianej siły fikcyjnej. Tę ostatnią siłę, czyli 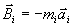, równą co do wartości iloczynowi masy i przyspieszenia, a przeciwnie do tego przyspieszenia skierowaną (rys.23.4), na­zywamy siłą bezwładności albo siłą d'Alemberta. Ponieważ dla każdego punktu materialnego rozpatrywanego układu moż­na ułożyć równanie typu (23.13), z rozważań powyższych wy­nika więc następująca zasada:

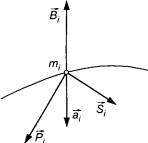
     Rys. 23.4

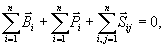
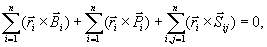                                                                                                                                          (23.14)

przy czym 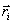 oznacza tu promień-wektor punktu m_i  poprowadzony z obranego bieguna 0. Ponieważ

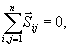
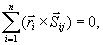
przeto równania (23.14) upraszczają się i przybierają postać:

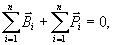
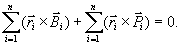                                                                                                                                               (23.15)

Uwzględniając, że 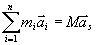, gdzie M oznacza masę całkowitą, a 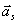- przyspieszenie środka masy, pierwsze z równań (6.15) można zastąpić następującym równaniem:

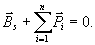                                                                                                                                              (23.16) 

Jeżeli biegun 0 obierzemy jako początek układu współrzędnych Oxyz, na którego osie rzutujemy równanie (23.16) i drugie z równań (23.15), to otrzymamy sześć równań równowagi dla sił rzeczywistych i sił bezwładności:

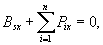
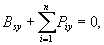
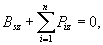
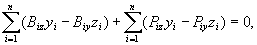
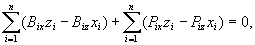
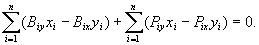
Wynikające z zasady d'Alemberta równanie wektorowe (23.15), jak też odpowia­dające im równania skalarne (23.17) nie zawierają sił wewnętrznych i są dogodne w za­stosowaniu do badania ruchu ciała sztywnego.
W ciele sztywnym siły wewnętrzne za­wsze się równoważą i nie mają wpływu na ruch tego ciała.
Przykład 1.
    Poziomy silnik tłokowy ustawiono na gładkim po­ziomym fundamencie (rys. 23.3). Korba OA o dłu­gości r obraca się ze stałą prędkością kątową . Przyjmując, że długość łącznika jest równa długości korby, i zakładając, że masy poruszających się części zredukowano do dwóch mas m1 i m2 umieszczonych na końcu korby i środku tłoka oraz że korpus silnika jest przymocowany do fundamentu za pomocą śrub, wyznaczyć sumaryczną po­ziomą siłę działającą na śruby i nacisk na fundament.

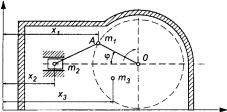
 Rys. 23.3

 Rozwiązanie:
    Korzystamy z dwóch pierwszych równań (23.11)

     

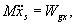
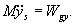
Ponieważ:

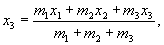
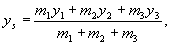
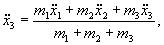
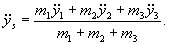
Mamy:

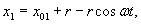
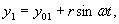
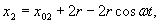
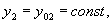
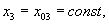
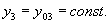
Stąd:

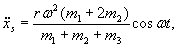
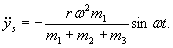
A zatem:

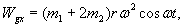
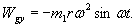
Z drugiej strony wiemy, że:

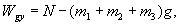
czyli nacisk na fundament wynosi:

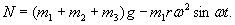
Sumaryczna siła działająca na śruby jest równa:

Rys. 23.5

Rozwiązanie:
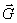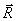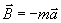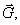
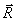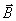    Przykładamy do windy siły działające: ciężar windy , siłę reakcji liny (rys. 23.5a) oraz fikcyjną siłę bezwładności . Wówczas suma geometrycz­na sił    i  jest równa zeru:

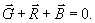
Ponieważ siły te leżą na jednej prostej, więc:

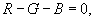
skąd:

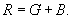
Moduł przyspieszenia 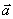,  jest równy

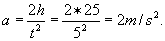
Moduł siły bezwładności:

                                                                                                                                                                              

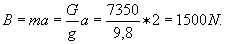
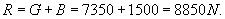
Przy ruchu windy w dół z tym samym przyspieszeniem (rys. 23.5b): 

skąd:

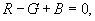
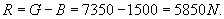
Przy ruchu jednostajnym windy (zarówno w górę, jak i w dół) a = 0, B = 0 i dlatego R = G = 7350N.

Pytania i ćwiczenia  sprawdzające.  

    1. Co rozumiemy pod pojęciem układ punktów materialnych?
    2. Co to są siły wewnętrzne?
    3. Co to są siły zewnętrzne?
    4. Co to jest środek masy układu?
    5. Podać zasadę ruchu środka masy.

    6. Podać zasadę zachowania ruchu środka masy.
    7. Podać zasadę d'Alemberta

 Ćwiczenia:

1.  Dwa ciała o ciężarach G₁ i G₂, połączone nierozciągli­wą bezmasową nicią przerzuconą przez krążek A, ślizgają się po idealnie gładkich płaszczyznach prostokątnego kli­na, opierającego się podstawą BC na gładkiej poziomej płaszczyźnie (rys. 23.6). Znaleźć, o ile przesunie się klin po poziomej płaszczyźnie przy opuszczeniu ciała o cię­żarze  o h = 10 cm. Ciężar klina G = 4G₁ = 16G₂. Masę krążka pominąć.

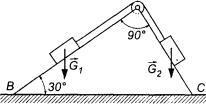
                                                                                     Rys. 23.6

Odpowiedź:
    W lewo na odległość 1,43 m.