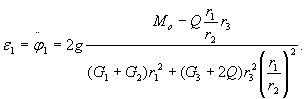
Temat 28 :   Równania Lagrange'a
             

28.1. Współrzędne uogólnione.

    Położenie układów punktów materialnych lub ciał sztywnych określamy za pomocą pewnych liczb. W szczególności liczby te są współrzędnymi punktów względem przyjętego układu odniesienia. Mogą to być współrzędne kartezjańskie, walcowe, sferyczne itp.
    Współrzędne te nie są na ogół niezależne. Muszą one czynić zadość równaniom wyrażającym właściwości więzów układu, ograniczających jego swobodę.
Wygodniej jest opisywać położenie układu za pomocą parametrów, które są już między sobą niezależne. Mogą to być wielkości zupełnie dowolne.

   Rozpatrzmy układ złożony z n punktów materialnych. Założymy, że każdemu położeniu układu punktów, które jest zgodne z więzami, przyporządkowane jest s liczb w taki sposób, że różnym położeniom układu punktów przyporządkowane są różne układy liczb q₁ ,...,q_s.
Współrzędne x₁, y₁, z₁ ,..., x_n, y_n, z_n  układu punktów są funkcjami zmiennych q₁,..., q_s, co można zapisać w postaci

x_i  =  f_i(q₁, q₂,..., q_s),
y_i  = g_i(q₁, q₂,..., q_s),                                                                                                                                       (28.1)                            
z_i  = h_i(q₁, q₂,..., q_s),

O funkcjach f_i,  g_i, h_i, zakładamy na ogół, że są w pewnym obszarze zmiennych q₁,..., q_s . Ciągłe wraz z pochodnymi cząstkowymi oraz to, że różnym układom liczb q1,..., q_k odpowiadają w tym obszarze różne układy liczb x₁, ..., z_n.. Więzy dwustronne układu określone mogą być funkcjami:

   F_j(x1, ..., z_n) = 0, j=1,2,...k                                                                                                                                                                
                                                                                                                                                                                                          (28.2)    
 Z równań tych możemy na ogół wyznaczyć k niewiadomych znając pozostałych s = 3n - k. Obierając więc dowolnie s zmiennych spośród  _x1, ..., z_ni oznaczając je symbolami q₁,...,q_s, będziemy mogli zmienne x1, ..., z_n przedstawić jako funkcje zmiennych q₁,...,q_s. Ponieważ dowolnie obranym wartościom q₁,...,q_s odpowiadają zmienne  x1, ..., z_n, spełniające układ równań  (28.1), więc parametry są niezależne.
    Liczba  s = 3n - k   nazwana została liczbą stopni swobody układu.
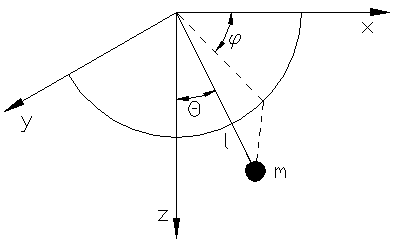
Wynika więc z tego, że liczba współrzędnych uogólnionych równa się liczbie stopni swobody układu;na przykład w przypadku wahadła sferycznego możemy określić położenie punktu za pomocą dwóch kątów φ i θ. Te dwie niezależne wielkości można obrać za współrzędne uogólnione (rys.28.1)  
   Współrzędne kartezjańskie wyrażają się wówczas równaniem:

   x = l sin θ cos φ,

   y = l sin θ sin φ,

   z = l cos θ.

   Niech więzy określone będą równaniami (28.1).  Jeżeli nadamy układowi dowolny ruch zgodny z wię­zami, to q₁,...,q_s będą funkcjami czasu. Różniczkując wyrażenie (28.1), otrzymujemy:  

Rys. 28.1

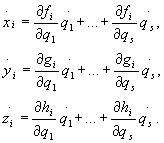                                                                                                                                                     (28.3)                                       Przesunięcia przygotowane otrzymujemy, przyjmując:

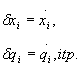
stąd

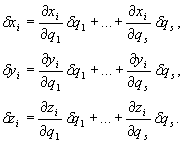                                                                                                                                                                        (28.4)

   Wyrazimy teraz pracę przygotowaną we współrzędnych uogólnionych. W tym celu w wyrażeniu (27.16) zamiast δx_i, δy_i, δz_i, podstawimy wyrażenia (28.4). Otrzymamy wówczas:

                                      (28.5)                          

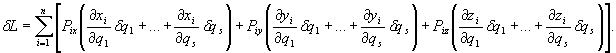
   Porządkując według δ_q1,..., δq_s, otrzymujemy:

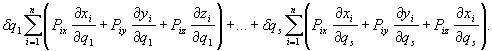
   Sumy występujące przy współczynnikach δq1,..., δq_s oznaczymy następująco:

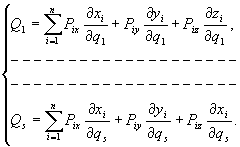                                                                                                                      (28.6)         

   Wyrażenie (28.6) można krócej zapisać:

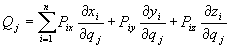      ,  j = 1, ..., s.                                                                                                                                                                                    (28.7)

   Wyrażenie Q, określone wzorem  (28.7) nazywamy siłami uogólnionymi. Ostatecznie praca przygotowana we współrzędnych uogólnionych określona jest następująco:

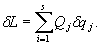                                                                                                                                                                                                                                                                      (28.8)

28.2. Równania Lagrange'a I rodzaju.

Na mechaniczny układ n materialnych punktów nałożone zostały holonomiczne stacjo­narne więzy typu

   f_r(x₁, y₁, z₁, ..., x_n, y_n, z_n) = 0,    r = 1, 2, k                                                                                                                                                                          (28.9)

  Te więzy nakładają się na wirtualne przemieszczenia k związków, które można otrzymać biorąc różniczki zupełne z lewych stron równań (28.9). Będziemy więc mieli:

  
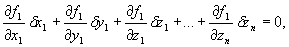
---------------------------------------------------                                                                                               (28.10)                                                                                                                                                                                                                                                                                                                                                                                                                           

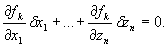
   Wiadomo, że z 3n przemieszczeń wirtualnych punktów rozpatrywanego układu mechanicznego δx₁, ..., δz_n  niezależnych będzie tylko (3n - k).

   Jeżeli z równań (28.10) znajdziemy k zależnych przemieszczeń jako funkcji (3n - k) niezależnych, a następnie podstawimy ich wartości do podstawowego równania mechaniki, to przyrównując do zera współczynniki przy niezależnych przemieszczeniach otrzymujemy  (3n - k) równań ruchu. Wtedy współczynnik przy przemieszczeniu różnym od zera będzie równy zeru na podstawie wyrażenia (27.41). Powtarzając to rozumowanie dla dowolnego niezależnego przemieszczenia przekonamy się, że współczynniki przy nich równe są zeru. Zatem, z wyrażeń (27.41) otrzymamy:

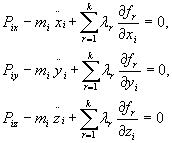                                                                                                                                                                     (28.11a) 

  lub

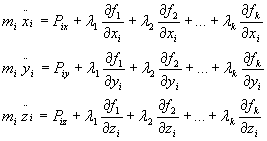                                                                                                                                                                                     (28.11b)                                                                                                                                                                                                      Równania (28.11b) nazywają się równaniami Lagrange'a I rodzaju dla układu holonomicznego.

Przyłączając do tych równań k równań więzów, otrzymujemy układ 3n równań, z których można określić 3n współrzędnych  x1, y₁, z₁, ..., z_n  w funkcji czasu i dowolnych stałych całkowania. Taki sposób otrzymywania dynamicznych równań ruchu jest skomplikowany. Posłużymy się dlatego mnożnikami Lagrange'a.
    Pomnożymy równania (28.10) odpowiednio przez λ₁, λ₂, ..., λ_k  i połączymy je z równaniami (27.41). Łącząc współczynniki przy rzutach przemieszczeń wirtualnych, otrzymujemy:

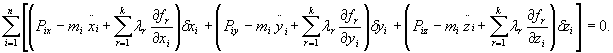                                            (28.12)                                 

   Korzystając z dowolnego wyboru mnożników Lagrange'a λ_r wybierzemy je tak, aby współczynniki przy k zależnych przemieszczeniach obracały się w zero. Wtedy współczynniki przy (3n - k) niezależnych przemieszczeń także będą równe zeru.
    Mając (3n - k) niezależnych przemieszczeń, możemy (3n - k - 1) z nich przyjąć równe zeru.

28.3. Równania Lagrange'a II rodzaju.

    Dany jest układ n punktów materialnych o masach m_i mający s stopni swobody. Położenie tego układu określone jest za pomocą wektora-promienia wodzącego  , który zależy od współrzędnych uogólnionych  q₁, ..., q_s i czasu t:

                                                                                                                                         (28.13)                      Prędkość i-tego punktu układu określona jest wzorem:

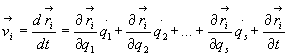                                                                                                            (28.14a)                                                                                                                                 

lub

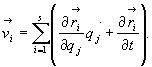                                                                                                                                        (28.14b)            

W przypadku więzów stacjonarnych

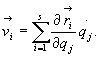                                                                                                                                                                                                                                                                                                                                                         (28.15)

Z wyrażenia (28.15) wynika, że pochodna cząstkowa względem jakiejkolwiek prędkości uogólnionej  równa jest współczynnikowi przy  w prawej części tego wyrażenia, tj. równa pochodnej cząstkowej od  względem współrzędnej q_j :

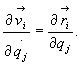                                                                                                                                                                                                                                                                                                                                                              (28.16)
Energia kinetyczna układu jest określona wzorem:

                                                                                                                                                                                                                                                                                                                                       (28.17)      
    Z wyrażenia (28.14a) wynika, że prędkość dowolnego punktu w przypadku więzów holonomicznych nie stacjonarnych jest funkcją współrzędnych uogólnionych, prędkości uogólnionych i czasu. Dlatego energia kinetyczna układu zależy także od tych zmiennych:

                                                                                                                            (28.18)                      Znajdziemy pochodną cząstkową energii kinetycznej względem współrzędnej uogólnionej q_j oraz względem prędkości uogólnionej :

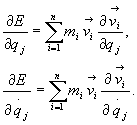                                                                                                                                          (28.19)               
Uwzględniając wyrażenie (28.16), otrzymujemy:

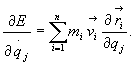                                                                                                                                          (28.20) 

Zróżniczkujemy to wyrażenie względem czasu:

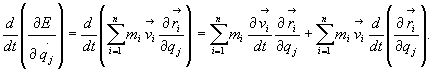                                                                                                                                                                                                                                                                                     (28.21
Wiadomo, że:

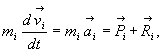                                                                                                                                    (28.22)   
dlatego

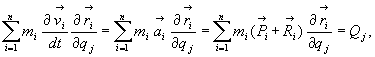                                                                                                                                                                                                                                                                                                 (28.23)                        gdzie Q_j  jest silą uogólnioną.

   W celu określenia wartości drugiej sumy we wzorze  (28.21)  rozpatrzymy wyrażenie:

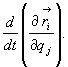
   Cząstkowa pochodna  jest funkcją tych samych zmiennych, co i wektor-promień wodzący . Różniczkując  jako złożoną funkcję czasu,otrzymujemy :

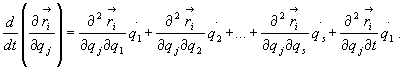                                                                                                                                                                                                                                                                                                                                          (28.24)
 Znajdziemy teraz cząstkową pochodną  różniczkując względem q_j  wyrażenie  (28.14):

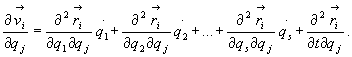                                                                                                                                                                                                                                                                                                        (28.25)

   Widzimy, że prawe strony wyrażeń  (28.24) i (28.25)  są sobie równe. Mamy więc:

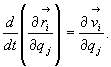                                                                                                                                                                                                                                                                                                                                                          (28.26)  

   Posługując się tą zależnością, przekształcamy drugą sumę prawej strony wyrażenia (28.21)

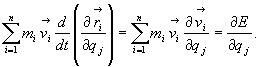                                                                                                                                                                                                                                                                                                                             (28.27)

   Podstawiając to wyrażenie do równania (28.21), otrzymujemy:

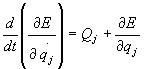                                                                                                                                                                                                                                                                                                                                                                              (28.28a)    
 lub

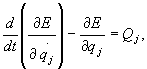    gdzie   j = 1, 2, ..., s.                                                                                                                                                                                                                                                                                                                                                            (28.28b)

    Układ równań (28.28a) nazywamy równaniami Lagrange'a II rodzaju. Przedstawiają one układ równań różniczkowych drugiego rzędu względem współrzędnych uogólnionych.

    Rozpatrzmy szczególny przypadek, kiedy siły działające mają potencjał V w każdej chwili t, przy czym:

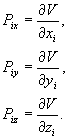                                                                                                                                                                    (28.29)
Siła uogólniona  Q_j  jest więc równa:

                                                                                                                                               (28.30)
gdzie U jest energią potencjalną układu.

   Podstawiając ostatnie wyrażenie do równania (28.28b), otrzymujemy:

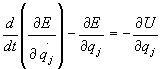                                                                                                                                       (28.31a)                                          
   lub

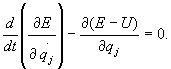                                                                                                                                       (28.31.b)                                      
Ponieważ energia potencjalna U nie zależy od prędkości uogólnionych  , więc

    
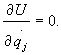
Zatem

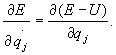                                                                                                                                                                                                                                                                                                                                                      (28.33)
Mamy więc

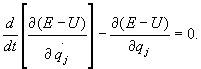                                                                                                                               (28.34)                             

   Wyrażenie E - U nazywamy potencjałem kinetycznym i oznaczamy symbolem W. Ostatecznie równania Lagrange'a II rodzaju w polu potencjalnym przyjmują postać:

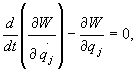      gdzie  j = 1, 2, ..., s.     (28.35)                                                                                                                                                                                                    16.4. Równania kanoniczne Hamiltona.

    Równania Lagrange'a drugiego rodzaju przedstawiają układ równań różniczkowych drugiego rzędu względem współrzędnych uogólnionych. Liczbarównań Lagrange'a odpowiada liczbie stopni swobody. Hamilton pokazał, że układ s równań Lagrange'a może być przedstawiony za pomocą 2s równań różniczkowych pierwszego rzędu.
     Równania Hamiltona są wygodne przy rozwiązywaniu szeregu zagadnień dynamiki układu, a także przy rozwiązywaniu współczesnych problemów mechaniki statystycznej oraz elektrodynamiki.
Hamilton wprowadził obok współrzędnych uogólnionych q₁, ..., q_s, s nowych zmiennych p₁, p₂, ..., p_s, które nazwano impulsami uogólnionymi.
Impulsy uogólnione są następującymi wyrażeniami:

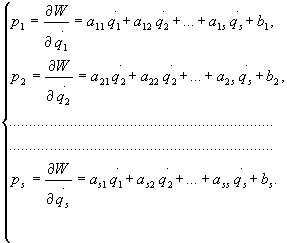                                                                                                                                                                                                                                                                                                                      (28.36)

Równania Lagrange'a drugiego rodzaju (28.35), uwzględniając (28.36), można napisać w postaci:

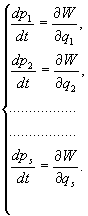                                                                                                                                                      (28.37)                    

Wprowadzimy teraz nową funkcję

                                                                                                                                             (28.38)              
z której wyeliminujemy prędkości uogólnione za pomocą wyrażeń (28.36).

   Rozwiązując równania (28.36) znajdujemy:

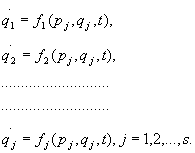
   Podstawiając otrzymane wyrażenia na prędkości uogólnione do wyrażenia (28.38) oraz obliczając różniczkę zupełną funkcji H, przy stałym t, otrzymujemy:

                                                                                                       (28.39)

   Obliczymy teraz:

    
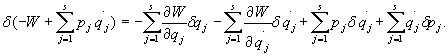
Wyrażając pochodne funkcji Lagrange'a przez impulsy uogólnione i ich pochodne mamy:  

                                                     (28.40)

   Podstawiając wyrażenie (28.40) do prawej części równania (28.39), otrzymujemy:

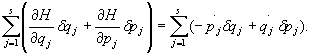
   Porównując w ostatnim wyrażeniu współczynniki przy niezależnych różniczkach, otrzymujemy:

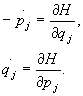                                                                                                                                                                                                                                                                                                                                                                                                              (28.41)

Równania (28.41) nazywają się równaniami kanonicznymi Hamiltona, a funkcja H zależna od 2s zmiennych kanonicznych q₁, q₂, ..., q_s, p₁, p₂, ..., p_s oraz czasu t nazywa się funkcją Hamiltona.
    Jeżeli nałożone na układ więzy są stacjonarne (skleronomiczne), to funkcja Ha­miltona ma prosty fizyczny sens. W tym przypadku H równa jest całkowitej energii układu.
Przy więzach stacjonarnych energia kinetyczna jest jednorodną funkcją kwadrato­wą prędkości uogólnionych. Mamy więc:

                                                                                                                                                                                                                                                                                                                            (28.42)              
Ponieważ funkcja Lagrange'a jest równa:

W = E - U

funkcję Hamiltona można przedstawić w postaci:

   H = E + U.                                                                                                                                                                                                                                                                                          (28.43)

Przyjmując φ  i  z  za zmienne niezależne, jako współrzędne uogólnione przyjmujemy:

   q₁ = φ,

   q2 = z.

   Impulsy uogólnione będą określone na podstawie równań (28.36)

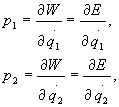
ponieważ energia potencjalna niezależna jest od prędkości uogólnionych.

   Stąd mamy:

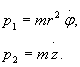
   Obliczając z ostatnich wyrażeń   i    i wstawiając je do wzoru na energię kinety­czną, otrzymujemy:

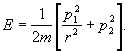
Ponieważ energia potencjalna jest równa:

    
więc funkcja Hamiltona przybierze postać:

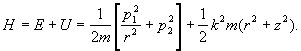
Równania Hamiltona na podstawie (28.41) mają postać:

    
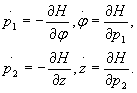
Po podstawieniu wartości otrzymamy:

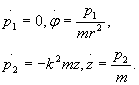
Przykład:

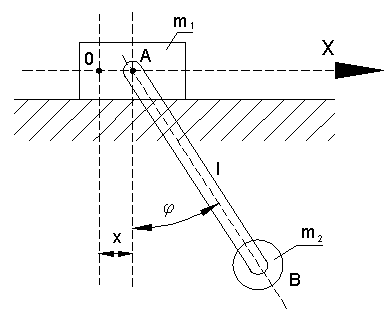
   Napisać równania ruchu wahadła eliptycznego składającego się z suwaka o masie m₁ ślizgającego się bez tarcia po płaszczyźnie poziomej i kulki o masie m₂ połączonej z suwakiem za pomocą pręta o długości l . Pręt może się obracać dookoła osi A związanej z suwakiem i prostopadłej do płaszczyzny rysunku. Masę pręta pominąć.

Rozwiązanie:

    Układ posiada 2 stopnie swobody.
Jako współrzędne uogólnione przyjmujemy kąt obrotu pręta φ i przemieszczenie suwaka x
Obliczamy energię kinetyczną układu:

  
Współrzędne punktu B:

       ;  

          ;  

zatem

    
Ostatecznie energia kinetyczna układu jest równa:

Obliczamy energię potencjalną układu:

  
Obliczamy potencjał kinetyczny:

    
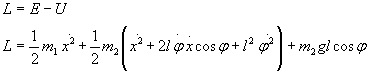
Dla układu mamy dwa równania Lagrange'a dla współrzędnej x i dla współrzędnej φ:

    
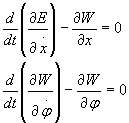
Wstawiając wyrażenia na potencjał kinetyczny i dokonując różniczkowania otrzymamy ostatecznie równania różniczkowe ruchu wahadła eliptycznego:

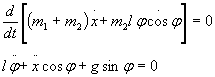
Pytania i ćwiczenia sprawdzające:

1. Co to są współrzędne uogólnione?
2. Dla jakiego rodzaju więzów można stosować równania Lagrange'a I rodzaju?
3. Podać równania Lagrange'a II rodzaju.
4. Podać równania Lagrange'a II rodzaju w polu potencjalnym.
5. Co to jest potencjał krytyczny?
6. Podać równania kanoniczne Hamiltona.

Ćwiczenie:

Koło zębate l o ciężarze G₁ i promieniu r₁ porusza się na skutek działania pary sił o momencie M₀ i na­pędza koło 2 o ciężarze G₂ i promieniu r₂. Koło 2 związane jest sztywno z walcem o promieniu r₃ i cię­żarze G₃. Na walec trzy nawija się nić, na końcu której zawieszony jest ciężar Q. Określić przyspieszenie ką­towe koła l, uważając koła zębate l i 2 za jednorodne walce. Ciężar nici pominąć.

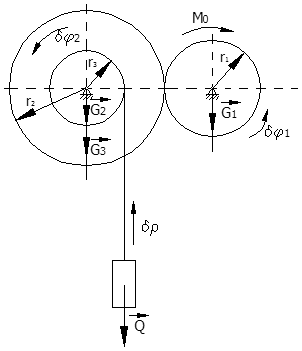
Odpowiedź: