Temat 4: Twierdzenie
o trzech siłach.
Środkowy(zbieżny) układ sił.
4.1.Twierdzenie o trzech siłach.
Rozpatrzmy przypadek, kiedy
dany układ trzech sił nierównoległch, działających w jednej płaszczyźnie,
przyłożony jest do bryły sztywnej w punktach 1,2,3 (rys. 4.1). Dwie
siły P1
i
P2
zastępujemy
jedną siłą S=P1+P2
i
pytamy, przy jakich warunkach siła P3
tworzy dwójkę zerową z siłą S.
Pierwszym
warunkiem jest to, aby siła
P3
działała wzdłuż prostej działania siły S,
czyli
jej prosta działania musi przechodzić przez punkt A. Drugim warunkiem
jest, aby miała tę samą wartoŚć i przeciwny
zwrot. Ten drugi warunek przedstawiono na rysunku graficznie, to znaczy
trójkąt sił P1,
P2, P3 musi
być zamknięty.
Opierając się na analizie
tego układu sił (Środkowy) można wykazać następujące
twierdzenie:
Trzy siły są w równowadze, jeżeli ich proste
działania przecinają się w jednym punkcie, leżą w jednej płaszczyźnie i
trójkąt sił jest trójkątem zamkniętym.
 4.2. Układy sił
4.2. Układy sił
Układ sił - jest to
zbiór sił przylożonych w jednym lub w kilku punktach bryły.
1. Środkowy (zbieżny) układ
sił (płaski lub przestrzenny),
2. Dowolny
układ sił (płaski lub przestrzenny) .
Układ
sił równoległych (szczególny przypadek dowolnego układu sił)
Najprostszy układ sił w równowadze - dwójka
zerowa.
Środkowy układ sił (płaski i przestrzenny)
- układ, w którym proste działania sił
przecinają sie w jednym punkcie.Taki
układ sił można zastąpić jedna siłą (wypadkową tego układu), albo sprowadzić
do dwójki zerowej (układ sił jest wtedy w równowadze).
Dowolny układ sił (płaski i przestrzenny)-
układ, w którym proste działania sił są dowolnie położone
wzgledem siebie tzn. nie przecinają się w jednym
punkcie.
Układ sił równoległych-
szczególny przypadek dowolnego układu sił, w którym proste działania wszystkich
sił są do siebie równoległe.
4.3. Analityczne przedstawienie
siły i wieloboku sił
Dotychczsowe konstrukcje przeprowadzalismy
na podstawie rachunku wektorowego. Rachunek wektorowy możemy zastąpić rachunkiem
algebraicznym. W tym celu wprowadzamy układ współrzędnych, w którym siłę
okreŚlamy rzutami wektora siły na osie układu
wspólrzędnych.
Najwygodniej jest przyjmować układ prostokątny
prawoskrętny.
 Na rys. 4.2 Px
i Py są współrzędnymi wektora siły P.
Wspólrzędne siły nazywać będziemy miarami rzutów siły na odpowiednie osie
układu współrzędnych.
W przypadku siły
na płaszczyźnie (rys.powyżej) współrzędne
wektora siły P okreŚlone
są wzorami:
Na rys. 4.2 Px
i Py są współrzędnymi wektora siły P.
Wspólrzędne siły nazywać będziemy miarami rzutów siły na odpowiednie osie
układu współrzędnych.
W przypadku siły
na płaszczyźnie (rys.powyżej) współrzędne
wektora siły P okreŚlone
są wzorami:
 Siła P tworzy kąt a
z
osią x.
Siła P tworzy kąt a
z
osią x.
Siła P wyrażona za pomocą
jej współrzędnych i wektorów jednostkowych jest równa:
 Jeżeli podane są współrzędne wektora siły, możemy
okreŚlić wartoŚć
siły i znaleźć prostą jej działania. WartoŚć
siły obliczamy ze wzoru:
Jeżeli podane są współrzędne wektora siły, możemy
okreŚlić wartoŚć
siły i znaleźć prostą jej działania. WartoŚć
siły obliczamy ze wzoru:
 Prostą działania siły P
(jej kierunek działania) wyznaczamy obliczając kąty ze wzorów:
Prostą działania siły P
(jej kierunek działania) wyznaczamy obliczając kąty ze wzorów:
 Rzut sumy geometrycznej na dowolną oŚ
równa się sumie rzutów na tę oŚ wszystkich
sił.
Suma geometryczna sił równa się wektorowi
głównemu
Wg.
Współrzędne wektora głównego (w przypadku płaskiego
Środkowego
układu sił) okreŚlone są wzorami, a prostą
działania wyznaczamy okreŚlając kąt:
Rzut sumy geometrycznej na dowolną oŚ
równa się sumie rzutów na tę oŚ wszystkich
sił.
Suma geometryczna sił równa się wektorowi
głównemu
Wg.
Współrzędne wektora głównego (w przypadku płaskiego
Środkowego
układu sił) okreŚlone są wzorami, a prostą
działania wyznaczamy okreŚlając kąt:
 Wspólrzędne wektora siły P w
przypadku siły w przestrzeni okreŚlone
są wzorami:
Wspólrzędne wektora siły P w
przypadku siły w przestrzeni okreŚlone
są wzorami:
 Siła P wyrażona za pomocą jej
wspólrzędnych i wektorów jednostkowych jest równa:
Siła P wyrażona za pomocą jej
wspólrzędnych i wektorów jednostkowych jest równa:
 Jeżeli podane są współrzędne wektora siły, możemy obliczyć wartoŚć
siły i znaleźć prostą jej działania. WartoŚć
siły obliczamy ze wzoru:
Jeżeli podane są współrzędne wektora siły, możemy obliczyć wartoŚć
siły i znaleźć prostą jej działania. WartoŚć
siły obliczamy ze wzoru:
 Prostą działania siły P wyznaczamy,
obliczając kąty ze wzorów:
Prostą działania siły P wyznaczamy,
obliczając kąty ze wzorów:
 Pomiędzy cosinusami kątów a, b, g , zawartych
pomiędzy siłą a osiami układu odniesienia, zachodzi związek:
Pomiędzy cosinusami kątów a, b, g , zawartych
pomiędzy siłą a osiami układu odniesienia, zachodzi związek:
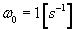 Jeżeli rozpatrujemy siłę P na
płaszczyźnie (układ odniesienia x,y) to
Jeżeli rozpatrujemy siłę P na
płaszczyźnie (układ odniesienia x,y) to  i
i  .
.
W ten sposób możemy przedstawić sumę geometryczną dowolnej liczby sił.
Rzut sumy geometrycznej na dowolną oŚ
równa się sumie rzutów na tę oŚ
wszystkich sił.
Suma geometryczna sił równa się wektorowi
głównemu
Wg.
Współrzędne wektora wektora głównego Wg(w
przypadku przestrzennego Środkowego układu
sił )są okreŚlone wzorami:
 WartoŚć wektora głównego
obliczamy na podstawie wzoru:
WartoŚć wektora głównego
obliczamy na podstawie wzoru:
 Prostą działania wektora głównego wyznaczamy, obliczając
kąty a, b, g,
zawarte między wektorem głównym Wg,
a osiami układu:
Prostą działania wektora głównego wyznaczamy, obliczając
kąty a, b, g,
zawarte między wektorem głównym Wg,
a osiami układu:
 4.4. Równowaga Środkowego
układu sił
4.4. Równowaga Środkowego
układu sił
Jeżeli
wielobok sił jest zamknięty (geometryczny warunek równowagi układu sił),
to suma geometryczna sił jest zerem, czyli Wg=0,
lub



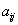 Równania te wyrażają analityczny zapis warunku równowagi płaskiego Środkowego
układu sił.
Równania te wyrażają analityczny zapis warunku równowagi płaskiego Środkowego
układu sił.
Warunkiem koniecznym i wystarczającym równowagi
płaskiego
Środkowego
układu sił jest,
aby algebraiczne sumy rzutów wszystkich sił na dwie osie prostokątnego
układu odniesienia były równe zeru (dwa równanai
równowagi).
Jeżeli siły działają w przestrzennym układzie
współrzędnych x,y,z, to otrzymamy trzy równania równowagi.
 Są to równania wyrażające analityczny zapis
warunku równowagi przestrzennego Środkowego
układu sił.
Są to równania wyrażające analityczny zapis
warunku równowagi przestrzennego Środkowego
układu sił.
Warunkiem koniecznym i wystarczającym równowagi
przestrzennego
Środkowego
układu sił jest,
aby algebraiczne sumy rzutów wszystkich sił na trzy osie prostokątnego
układu odniesienia były równe zeru.
Przykład:
Na dwóch, prostopadłych do siebie, gładkich równiach
pochyłych AB i BC spoczywa kula o ciężarze Q = 12N (rys.
4.4). OkreŚlić reakcje działające na kulę
w punktach jej styku z płaszczyznami, jeżeli kąt .
.
 Rozwiązanie:
Rozwiązanie:
Przystępując do rozwiązania zadania, kulę
spoczywającą na dwóch gładkich powierzchniach równi pochyłych
AB
i BC, uwalniamy najpierw od więzów i przykładmy do niej oprócz siły
ciężkoŚci Q
odpowiednie
siły reakcji tj. RD i RE
(rys. 4.5).
 Reakcje te obrazują oddziaływanie powierzchni równi
pochyłych na kulę i przyłożone są w punktach styku kuli z tymi powierzchniami.
Ponieważ powierzchnie te są z założenia gładkie (nie występuje zjawisko
tarcia tzn. nie ma sił stycznych), więc reakcje RD i
RE
są prostopadłe do powierzchni kuli, a zatem ich proste działania przechodzą
przez punkt O czyli Środek kuli.
Reakcje te obrazują oddziaływanie powierzchni równi
pochyłych na kulę i przyłożone są w punktach styku kuli z tymi powierzchniami.
Ponieważ powierzchnie te są z założenia gładkie (nie występuje zjawisko
tarcia tzn. nie ma sił stycznych), więc reakcje RD i
RE
są prostopadłe do powierzchni kuli, a zatem ich proste działania przechodzą
przez punkt O czyli Środek kuli.
Zadanie można rozwiązać matodą analityczną i metodą
geometryczną.
Metoda analityczna - (korzystamy z analitycznych waruków
równowagi Środkowego układu sił).
Stosując analitycany sposób rozwiązania należy przyjąć
w punkcie O układ współrzędnych Oxy.
Poniważ kula znajduje się w równowadze, więc muszą być spełnione następujące
równania: 
Z powyższych równań zawierających dwie niewiadome RD
i
RE,
otrzymujemy:
 Ponieważ
Ponieważ  , więc po podstawieniu
wartoŚci, otrzymamy:
, więc po podstawieniu
wartoŚci, otrzymamy:
 Metoda geometryczna - (korzystamy z geometrycznego warunku równowagi
Środkowego
układu sił)
Metoda geometryczna - (korzystamy z geometrycznego warunku równowagi
Środkowego
układu sił)
Poniważ kula znajduje się w równowadze, więc siły
Q,
RD
i
RE muszą tworzyć wielobok sił
zamknięty (w tym przypadku trójkąt) - rys.4.6.
 Z trójkąta tego znajdujemy:
Z trójkąta tego znajdujemy:
 .
.
Pytania i ćwiczenia sprawdzające.
1. Podać twierdzenie o trzech
siłach.
2. Podać analityczny sposób
przedstawienia siły i wieloboku sił.
3. Co rozumiemy pod pojęciem
wektora głównego (Wg )?
4. Jaki układ nazywamy Środkowum
(zbieżnym)?
5. Okreslić analityczne
warunki równowagi Środkowego
układu sił (płaskiego i przestrzennego).
Ćwiczenia:
1. Znaleźć reakcje podpór
A i B belki obciążonej, jak pokazano na rys. 4.3, gdy  oraz
oraz  (ciężar belki
pominąć).
(ciężar belki
pominąć).
 Odpowiedź: RA = 15800N
Odpowiedź: RA = 15800N
RB = 7100N






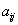

![]() .
.



![]() oraz
oraz ![]() (ciężar belki
pominąć).
(ciężar belki
pominąć).