Temat 13:  Opis matematyczny ruchu punktu

13.1.Wstęp. Zasadnicze pojęcia i okreŚlenia
    Kinematyka jest działem mechaniki, który zajmuje się badaniem ruchu ciał z pominięciem czynników fizycznych wywołujących ten ruch.
Stanowi ona pewnego rodzaju geometrię ruchu, gdyż zasadniczo  stosujemy w niej dwa podstawowe pojęcia - przestrzeń i czas. Przy rozpatrywaniu przemieszczeń ciał (lub odpowiadających im geometrycznych modeli: punktu, bryły), bierzemy pod uwagę również czas przemieszczenia. Dlatego  kinematyka nazywana jest nieraz "geometrią czterech wymiarów", w rozumieniu czasu jako czwartego
wymiaru.
    W mechanice klasycznej (stosującej zasady wprowadzone przez Newtona) czas uważamy za ten sam dla dowolnych układów odniesienia, co jest przybliżeniem w stosunku do rzeczywistoŚci wystarczająco dokładnym, gdy prędkoŚci rozpatrywnych ruchów są małe w porównaniu z prędkoŚcią swiatła.
     Za jednostkę czasu przyjmuje się sekundę. Chwili początkowej, którą możemy obierać dowolnie, przypisujemy wartoŚć równą zeru, a każdej natępnej liczbę t, której bezwzględna wartoŚć równa jest liczbie sekund, jakie upłynęły pomiędzy tymi dwoma chwilami. Ustanowienie odpowiednioŚci pmiędzy kolejnymi chwilami i zbiorem liczb rzeczywistych nazywa się jego arytmetyzacją i może być graficznie przedstawione prostą, zwaną osią czasu.
     Punkty tej prostej odpowiadają odpowiednim chwilom. Dla chwil późniejszych od początkowej t>0.
Każde ciało, którego ruch badamy, może być uważane za układ punktów materialnych. W kinematyce punkt materialny traktujemy jak punkt w pojęciu geometrycznym, któremu przypisujemy pewną skończoną masę.
    Szczególnym przypadkiem układu punktów materialnych jest bryła sztywna.
Ruch dowolnego układu punktów względem zadanego układu odniesienia będzie okreŚlony, jeżeli będziemy znać ruch każdego punktu względem tego układu odniesienia.
     Analizę  ruchu rozpoczyna się  od ruchu punktu stanowiącego najprostszy obiekt geometrczny, a w dalszej kolejnoŚci prowadzi  się  analize  układu punktów (bryły). Dlatego też kinematykę dzielimy ze względów dydaktycznych na kinematykę punktu i kinematykę bryły.
W przyjętym układzie odniesienia, związanym np. z trójwymiarową przestrzenią Euklidesową, obserwowany punkt materialny przechodzi przez punkty tej przestrzeni.
13.2. Kinematyka punktu. Sposoby opisania ruchu punktu

Torem albo trajektorią  punktu nazywamy linię ciągłą, będącą miejscem geometrycznym kolejnych położeń punktu w przestrzeni.
Tor może być krzywą płaską lub przestrzenną. Ruch punktu okreŚla się przez podanie prawa ruchu. Prawo (równanie) ruchu ustala zależnoŚć położenia punktu w przestrzeni od czasu.
Istnieje kilka sposobów opisu ruchu punktu:
1)  przez podanie wektora - promienia wodzącego punkt ruchomy w funkcji czasu,
2)  przez podanie współrzędnych kartezjańskich jako funkcji czasu, czyli tak zwanych równań
     skończonych ruchu,
3)  przez podanie toru i współrzędnej krzywoliniowej wzdłuż toru, okreŚlającej sposób poruszania się
     po torze,
4)  przez podanie innych współrzędnych krzywoliniowych jako funkcji czasu np: biegunowych,
     walcowych, sferycznych.
13.2.1. Ruch punktu opisany wektorem - promieniem wodzącym
    Położenie punktu M w przestrzeni okresla w każdej chwili promień - wektor (promień wodzący).
Wektor ten wykreslany z pewnego stałego punktu O (rys.13.1) okresla swym końcem położenie punktu. Ruch punktu może być więc okreŚlony przez podanie dla każdej chwili czasut wektora - promienia wodzącego r. ZależnoŚć wektora r od czasut może być przedstawiona w postaci wektorowego równania ruchu:
r = r(t)
ZależnoŚć ta okreslar jako wektorową funkcję zmiennej skalarnej t.
    Promień wodzący r punktu M można wyrazić przez współrzędne kartezjańskie i wektory jednostkowe i, j, k osi współrzędnych:      r = ix + jy + kz.

Miejsce geometryczne końców zmiennego wektora r, mającego stale początek w tym samym punkcie, nazywa się hodografem wektora - promienia wodzącego.
13.2.2. Ruch punktu opisany równaniami skończonymi (współrzędnymi prostokątnymi)
     Położenie punktu M w przestrzeni  okreslić możemy względem przyjętego, układu odniesienia za pomocą trzech współrzędnych x, y, z, prostokątnego układu współrzędnych (rys.poniżej).
W przypadku ruchu punktu funkcje x, y, z są ciągłymi funkcjami czasu:
x = f1(t);  y = f2(t);         z = f3(t).
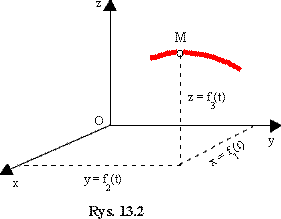
Jeżeli funkcje te są znane, to w każdej chwili t możemy okreslić położenie punktu M względem przyjętego układu odniesienia (rys.13.2). Równaia powyższe  nazywamy równaniami skończonymi ruchu. Przedstawiają one parametryczne równania toru (parametrem jest czas).
W celu znalezienia toru (trajektorii( punktu Mw postaci jawnej rugujemy z przedstawionych powyżej równań czs i otrzymujemy:
f1(x,y) = 0;     f2 (x,z) = 0
Te dwa otrzymane równania przedstawiają krzywą po której prusza się punkt.
13.2.3. Ruch punktu opisany współrzędną naturalną (łukową)
    Zalóżmy, że znany jest tor poruszającego się punktu M. W celu okreslenia położenia tego punktu na torze, obieramy dowolnie pewien punkt O toru. Położenie punktu M na torze okrelŚamy przez podanie łuku odmierzonego od punktu O do danego punktu M (rys.13.3).
DługoŚć łuku OM oznaczona symbolem s nazywa się współrzędną drogową  punktu ruchomego.
     Wcelu okreŚlenia po której stronie punktou O znajduje się badany punkt M, przyjmujemy umownie dodatni znak toru.
W dodatnią stronę od punktu O odmierzamy współrzędną dodatnią, a w ujmną stronę współrzędną ujemną.
W każdej chwili t położenie punktu M na torze możemy wyznaczać jeżeli znana jest funkcja
s = f(t)
ZależnoŚć ta nazywa się równaniem ruchu punktu na torze. Ruch punktu jest więc okreŚlony, jeżeli znane są: tor punktu (początek i kierunek odmierzania współrzędnej drogowej oraz  równanie ruchu
s = f(t).
    Współrzędnej drogowej punktu nie należy utożsamiać z  długoscią drogi  s* przebytej przez poruszający się punkt.
    Współrzędna drogowa s punktu M w pewnej chwili t może się równać drodze s*, przebytej prze punkt w czasie (0, t), tylko wtedy, gdy ruch punktu zaczyna się od punktu O i punkt porusza się w stronę dodatnią toru.
Przyjmując, że w chwili początkowej to punkt miał położenie Mo, a w chwili t położenie M, to droga przebyta w czasie (0, t) przy ruchu punktu w jedną stronę  wynosi
s* = MoM = OM - OMo = s - so

Zmiana współrzędnej  łukowej (drogowej) s w elementarnym czasie dt jest równa różniczce
ds = df(t)= f '(t)dt; przy ruchu punktu w stronę dodatnią ds > 0, a wstronę ujemną ds < 0.
Przyrost drogi ds (elementarne przemieszczenie) punktu) jest zawsze dodatni,
ds* = /ds/ = /f '(t)/dt.
Droga przebyta przez punkt w odstępie czasu (0, t)wynosi

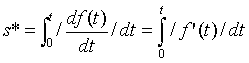Jeżeli ruch jest okreŚlony rówaniami skończonymi
x = f1(t);         y = f2(t);         z = f3(t)
to różniczkę współrzędnej łukowej obliczamy ze wzoru
a po przeprowadzeniu całkowania otrzymamy współrzędną łukową
13.2.4. Ruch punktu opisany współrzędnymi krzywoliniowymi
    Położenie punktu w przestrzeni można okreŚlić za pomocą współrzędnych krzywoliniowych. Przykładem tych współrzędnych są: współrzędne sferyczne i walcowe. W układzie sferycznym
(rys.13.4) jako współrzędne punktu M przyjmujemy:
a)  długosć r promienia wodzącego r,
b) kąt dwuscienny f między płaszczyzną Ozx i płaszczyzną OzM1,
c) kąt ymiędzy promieniem wodzącym r, a płaszczyzną Oxy.
W tym układzie równania ruchu mają postać:
r = r(t),         y = y(t),         f = f(t).
Powyżej zapisane współrzędne sferyczne są powiązane w następujący sposób ze współrzędnymi kartezjańskimi:
x = r cosy cosf,      y = r cosysinf,        z = r siny

            Liniami współrzędnych r są proste przechodzące perzez punkt O. Liniami współrzędnych fsą okręgi o Środku na  osi z (rówmoleżniki). Liniami współrzędnych ysą okręgi w płaszczyznach przechodzących przez oŚz(południki).
Jeżeli ruch punktu odbywa się na płaszczyźnie Oxy, to y = 0 = const. Ruch opisujemy wtedy dwoma współrzędnymi r oraz f. Te współrzędne nazywamy współrzędnymi biegunowymi.
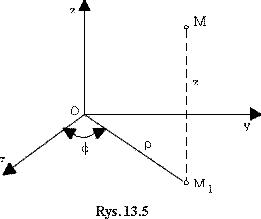
  W celu okreŚlenia położenia punktu M w przestrzeni można zastosować współrzędne walcowe
(rys.13.5):
a) współrzędną z w prostokątnym (kartezjańskim) układzie współrzędnych Oxy,
b) odległoŚć r punktu M od osi Oz,
c) kąt f  między płaszczyzną Ozx a płaszczyzną przechodzącą przez oŚOz  i  punkt M.
Równania ruchu są następujące:
z = z(t), r = r(t), f = f(t).
Między współrzędnymi walcowymi punktu M a jego współrzędnymi w prostokątnym układzie współrzędnych, zachodzą następujące związki:
x = r cosf,y = r sinf, z = z
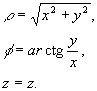
    Liniami współrzędnych są proste równoległe do osi Oz, a współrzędnych r proste prostopadłe
do osi Oz.
Liniami wspólrzędnychfsą okręgi o Środkach leżących na osi Oz.
Jeżeli współrzędna  z = const, to współrzędne walcowe  r i f  stają się współrzędnymi biegunowymi na płaszczyźnie.

Przykład:
    Punkt M porusza się zgodnie z równaniami:

x = 3 - 4 sin t
y =  4 cos t.
Wyprowadzić równanie toru po jakim prusza się ten punkt.
Rozwiązanie:
    Dla znalezienia równania toru w postaci f(x,y) = 0, należy z równań ruchu wyrugować parametr t, to znaczy czas.
Przekształcając powyższe równania otrzymamy:
x - 3 = - 4 sin t
y = 4 cos t
Podnosząc stronami do kwdratu:

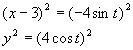
Dodając stronami otrzymamy:

Przekształcając i podstawiając za:   otrzymamy ostatecznie równanie toru:
Jest to równanie okręgu (rys. 13.6) o promieniu r = 4, którego Środek  leży w punkcie S o współrzędnych
xo = 3
yo = 0.

Pytania i ćwiczenia sprawdzające
    1. Co to jest kinematyka?
    2. Co to jest tor lub trajektoria punktu?
    3. Przez co okreŚla się ruch punktu?
    4. Co to jest (równanie) prawo ruchu punktu?
    5. Podać sposoby przedstawienia (opisania) ruchu punktu.
    6. Co to jest współrzędna drogowa punktu?

Ćwiczenia:
1. Dane są równania punktu M poruszającego się w jednej płaszczyźnie Oxy:
        a)  x = 5 + t;            y = 2t,
        b) x = 5 + 3 cos t,      y = 4 sin t.
        Wyznaczyć równanie toru punktu M.
Odpowiedź:
        a) półprosta x = 0,5y + 5 o początku w punkcie: xo= 5,   yo = 0.
        b) elipsa .

2.  Mając dane równania we współrzędnych biegunowych i walcowych, wyznaczyć równanie toru            punktu:

        a) f = kt,  r = b + 2c cos kt,
        b) 
Odpowiedź:
        a) r = b + 2c cos f,
   b)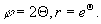
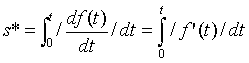
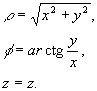
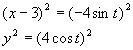