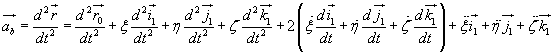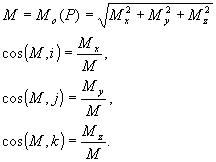Temat 6 :   Moment siły względem punktu
i względem osi

1. Moment siły względem punktu (bieguna)
        Momentem siły względem punktu (bieguna) nazywamy wektor Mo(P)taki, że:

Wektor momentu jest prostopadły do płaszczyzny wyznaczonej przez prostą działania siły i punkt.
Wartosć wektora momentu jest równa:

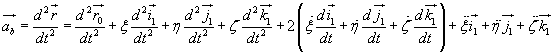
    Odległosć d  jest odległoscią  prostej działania siły od punktu i nazywana jest ramieniem siły.
Zwrot wektora momentu jest taki, aby patrząc od jego strzałki na płaszcyznę wyznaczoną przez siłę i punkt, widać było obrót siły względem punktu w kierunku przeciwnym do ruchu wskazówek zegara czyli inaczej, aby trójka wektorów zaznaczonych na rysunku była prawoskrętna.
Moment siły względem bieguna  jest  zerem, gdy prosta działania siły przechodzi przez ten biegun.
Z definicji momentu siły względem bieguna wynika, że moment nie zmieni się, jeżeli siłę przesuniemy wzdłuż  prostej działania.
2. Moment siły względem osi
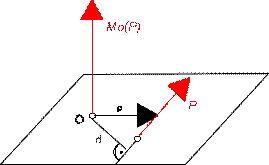
Przyjmijmy, że dane są: Punkt O (biegun) i siła P. W punkcie O przyjmujemy początek prostokątnego układu współrzędnych. Momentem siły P względem bieguna O jest wektor Mo(P), (rysunek poniżej).
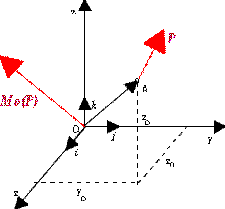Dowolny punkt A na prostej działania siły P ma współrzędne (xo, yo, zo).
Wektor siły P ma współrzędne Px, Py, Pz . Łącząc punkt A (xo, yo,zo) z początkiem układu otrzymamy wektor 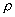 . Współrzędne wektora mpmentu siły P względem bieguna O oznazamy symbolami Mx, My, Mz .Współrzędne te można obliczyć jako minory niżej podanego wyznacznika, gdzie (i, j, k) są  wektorami jednostkowymi na osiach współrzędnych (wersorami):
                       i      j     k
Mo(P) = 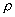 x P = xo   yo    zo
                      Px   Py   Pz
Po rozwiązaniu wyznacznika współrzędne momentu będą równe:
Mx  = Pzyo - Pyzo ,
My = Pxzo - Pzxo ,
Mz = Pyxo - Pxyo .
Współrzędne wektora momentu Mo(P)nazywami momentami siły względem odpowiedniej osi. Na przykład moment siły P względem osi Oz okrsela wzór:
Mz = Pyxo - Pxyo .
Wzór ten  zinterpretowany jest  geometrycznie w sposób pokazany na rysunku poniżej
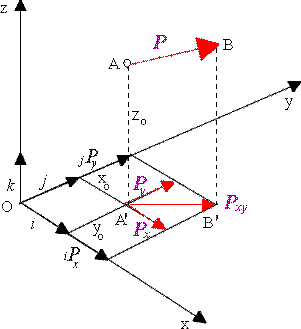Na podstawie tej interpretacji moment siły względem osi Oz  można okrelić jako moment rzutu siły P na płaszcyznę prostopadłą  do osi Oz względem punktu przebicia tej płaszczyzny przez os. Rzut siły P na płaszcyznę prostopadłą do osi oznaczony jest przez Pxy,  a punkt przebicia płaszczyzny Oxy przez os Oz  oznaczony symbolem O.
Z powyższego okrelenia momentu siły względem osi wynika, że moment siły względem osi jest zerem, gdy siła i os leżą w jednej płaszczyźnie (gdy siła jest równoległa do osi lub gdy prosta działania siły przecina os.
Korzystając ze wzorów na Mx, My, Mzmożemy obliczyć wartosć momentu siły P względem punktu O oraz okreslić kąty zawarte pomiędzy wektoremmomentu M a osiami układu:
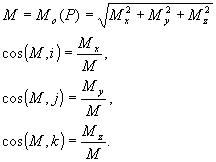Jeżeli siła leży w płaszcyźnie Oxy, to zo = 0 i Pz= 0 (patrz rysunek poniżej).
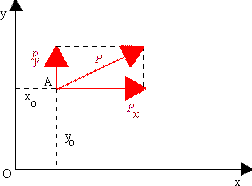Moment si ły P względem punktu (bieguna) O wynosi:
Mx = 0 ,
My = 0 ,
Mo(P) = Mz = Pyxo - Pxyo.
Znak momentu :
    - plus (+) - obrót siły dookoła osi O zgodnie z ruchem wskazówek zegara,
    - minus (-) - obrót siły dookoła osi O przeciwnie do ruchu wskazówek zegara.
3. Twierdzenie o równoległym przesuwaniu siły
    Załóżmy, że na bryłę działa siła P zaczepiona w punkcie A (rys. poniżej). Następnie chcemy tę siłę
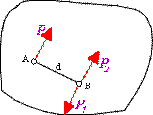przesunąć równolegle do punktu B. W tym celu w pukcie B przykładamy dwójkę zerową P1= -P2 równoległą do siły P przy czym P1=P2=P. Z rysunku widać, że układ sił składa się z teraz z siły P2 równej co do wartosci sile P oraz pary sił (P,P1), której wartosć momentu wynosi : M(P,P1)= Pd.
Przesunęlismy więc siłę P równolegle do nowego punktu zaczepienia B, przykładając jednak równoczesnie odpowiednią parę sił (P,P1).

4. Równowaga układów sił c.d.
    Dowolny układ sił
    Płaski dowolny układ sił (siły działają w jednej płaszcyźnie x,y) pozostaje w równowadze, jeżeli  wektor główny Wg = 0 i moment glówny  Mg = 0.  Zachodzi to gdy:
Wgx = 0,   Wgy = 0,   Mio = 0;  czyli gdy

Moment główny Mg jest to suma momentów sił Pi układu względem bieguna redukcji.
Analityczny warunek równowagi płaskiego dowolnego układu sił można sformułować następująco:
Warunkiem koniecznym i dostatecznym równowagi płaskiego dowolnego układu sił jest, aby sumy algebraiczne rzutów wszystkich sił na każdą z dwóch nierównolgłych osi równały się zeru i suma momentów wszystkich sił względem dowolnie obranego bieguna na płaszczyźnie działania tych sił była równa zeru (trzy równania równowagi).
Jeżeli siły działają w przestrzennm dowolnym układzie sił, to  pozostaje on w równowadze, jeżeli  Wg = 0,  Mg = 0.  Zachodzi to gdy:
Wgx = 0,  M gx = 0,
Wgy = 0,  Mgy = 0,
Wgz = 0,  Mg z = 0,     czyli gdy
Zatem przestrzenny dowolny układ sił pozostaje w równowadze, kiedy spełnionych jest szesć równań równowagi.
Warunkiem koniecznym i dostatecznym równowagi przestrzennego dowolnego układu sił jest, aby algebraiczne sumy rzutów wszystkich sił na trzy osie prostokątnego układu odniesienia były równe zeru oraz aby algebraiczne sumy momentów wszystkich sił względem tych trzech osi były równe zeru.
Układ sił równoległych (siły o równoległych prostych działania)
Suma rzutów sił na os równoległą  do kierunku działania sił (suma algebraiczna sił) oraz suma momentów względem dowolnego bieguna (dwa warunki równowagi).

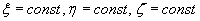
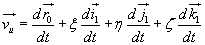Czasem mogą to być  dwa warunki równowagi momentów względem dwóch dowolnych biegunów.

Pytania i ćwiczenia  sprawdzające

    1. Moment siły względem punktu jako iloczyn wektorowy (rysunek). Podać jego własnosci,
    2. Moment siły względem osi.
    3. Okreslić analityczne warunki równowagi płaskiego i przestrzennego dowolnego układu sił,
    4. Podać równania równowagi układu sił równoległych.

Ćwiczenia:

    1. Obliczyć moment siły P względem początku układu współrzędnych gdy: Px=100N,  Py=200N,
a punkt początkowy ma współrzędne x = 3m,  y = -2m.
Odpowiedź:
M0(P) = 800k

    2. Belka AB o długosci l = 4,8m i ciężarze Q = 200N wsparta jest na dwóch podporach w punktach
C i D.
Dodatkowo na belkę działa pionowa siła P = 400N, para sił o momencie M0 = 200Nm, a na odcinku DE obciążenie ciągłe q = 7N/cm. Wyznaczyć reakcje podporowe belki w punktach C i D, jeżeli AC = DB = l/4 i CD = l/2.

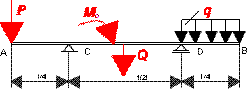Odpowiedź:
RC  = 408N
RD  = 1032N.