PROBLEM #3.2.5
Za jedno z bardziej ciekawych zagadnień, możemy uznać problem # 3.2.5 z książki Fukagawy i Pedoe.
Jest ono dość proste, ale zawiera wiele zaskakująco ciekawych właściwości.
W szczególności występuje użycie egipskiego trójkąta 3-4-5.
Mówi się, że wspomniane sangaku zostało napisane w 1838 roku i jego tabliczka nie przetrwała do dzisiaj.
W celu lepszego zrozumienia owego sangaku, posłużymy się dynamiczną kartą pracy.Dzięki niej możemy śledzić konstrukcję krok po kroku.
Na dole dynamicznej karty pracy znajduje się pasek z przyciskami sterowania. Możemy przewijać kroki,
uruchomić wyświetlanie się kolejnych elementów konstrukcji jeden po drugim, a także edytować czas wyświetlania pojedynczego kroku.
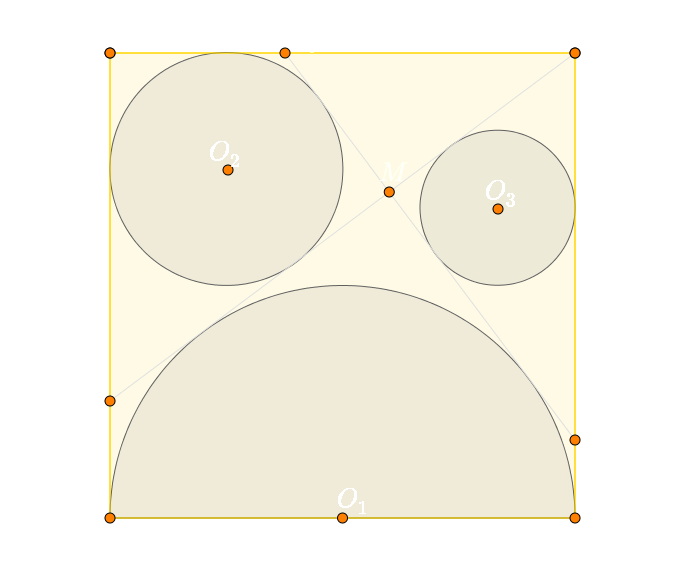
Dany jest kwadrat ABCD, w którym wpisane jest półkole w taki sposób, że odcinek AB jest jego średnicą ze środkiem w punkcie O1.
Odcinek CG, gdzie punkt G leży na odcinku AD, jest styczny do tego półokręgu, a okręg o środku w punkcie O2 i promieniu r2 jest okręgiem wpisanym w trójkąt CDG.
Zewnętrzna wspólna styczna półokręgu i okręgu o środku w punkcie O2 i promieniu r2 przecina bok CD kwadratu w punkcie R, a bok BC kwadratu przecina w punkcie N oraz przecina odcinek CG w punkcie M.
Okrąg O3 i promieniu r3 to okrąg wpisany w trójkąt CMN.
Udowodnij, że stosunek r2:r3=3:2
Ponieważ konfiguracja zawiera kilka egipskich trójkątów, warto najpierw ustalić następujące elementy.
Promień okręgu wpisanego w trójkąt o długości boku 3w, 4w, 5w, jest równy w.
Dowód jest prosty. Jak wiemy, w trójkącie prostokątnym z przyprostokątnymi a i b i o przeciwprostokątnej c, promień okręgu wpisanego w ten trójkąt jest równy (a + b-c) / 2. Tak więc dla egipskiego trójkąta mamy r = (3w + 4w-5w) / 2 = w.
Teraz należy zauważyć, że ΔCDG jest trójkątem egipskim. Możemy to bezpośrednio wyprowadzić.
Załóżmy dla wygody, że bok kwadratu wynosi 12.
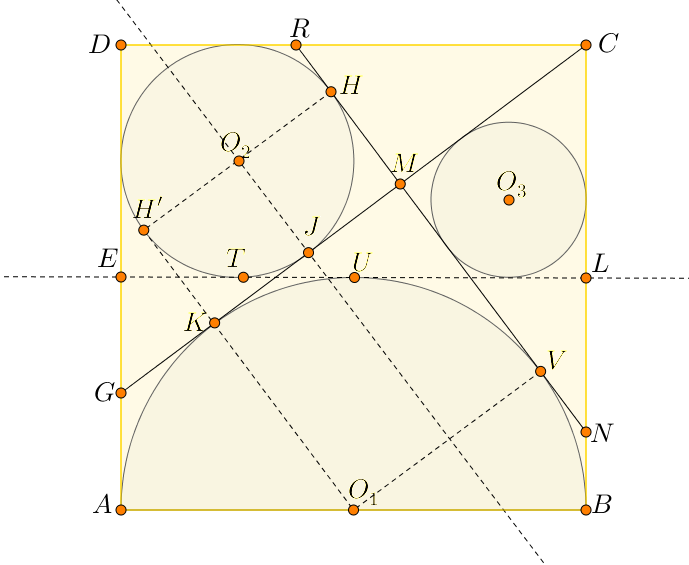
Niech K będzie punktem styczności odcinka CG i półkola. Następnie CK = CB = 12. Niech AG = GK = x. W ΔCDG, CG2 = CD2 + DG2, tak, że (12 + x)2 = 144 + (12-x)2, z którego x = 3. Oznacza to dokładnie, że boki ΔCDG wynoszą 9, 12 i 15, co czyni je egipskim trójkątem. Według Lemma, r2 = 3.
Oczywiście r1 = 6. Niech EL będzie linią środkową kwadratu ABCD, jak pokazano.
Teraz zauważmy, że linia EL jest styczna do półkola i okręgu o środku w punkcie O2. Niech U i T będą odpowiednimi punktami styczności. Jeśli J jest punktem styczności odcinka CG i okręgu w punkcie O2, to zarówno JK, jak i TU są wewnętrznymi wspólnymi stycznymi półkola i okręgu o środku w punkcie O2, co oznacza, że JK = TU = 3.
Niech KH'będzie odcinkiem stycznym do okręgu o środku w punkcie O2. Następnie należy przyjąć, że KH' = JK, w związku z tym KJO2H' jest rombem, a dodatkowo jeżeli JK⊥JO2 to KJO2H' jest kwadratem. Zatem H'K⊥KJ, czyli również H'K⊥CG.Zauważmy,że punkt K leży na odcinkku H'O1. Wynika z tego, że CG⊥H'O1 i H'O1 jest odcinkiem stycznym do okręgu o środku w punkcie O2 w punkcie H'.
Niech H i V, leżące na odcinku NR, będą punktami styczności odcinka NR odpowiednio z okręgiem o środku w punkcie O2 i okręgiem o środku w punkcie O1.Odcinek HV jest równoległy i równy odcinkowi H'O1, a więc HV⊥CG. Innymi słowy, CG⊥RN. Zatem trójkąty CNR, CMR i CMN, są podobne do trójkąta CDG, a zatem wszystkie są egipskie. Jako ostatni krok musimy ocenić "wielkość" trójkąta CMN.
Odkryliśmy już, że GK = AG = 3. Również JK = JM = 3. Tak więc GM = 9, natomiast CG = 15, dając CM = 6. Stąd promień okręgu wpisanego o środku w punkcie O3 jest równy 2.Podsumowując r2=3, a r3=2, czyli stosunek r2 do r3 wynosi 3:2, co rozwiązuje problem.
JAK BAWIĆ SIĘ KONSTRUKCJAMI?
Przykładów sangaku jest bardzo dużo. Ta strona zawiera kilka przykładów, lecz to nie znaczy, że inne są mniej ważne. Sangaku to nie tylko drewniane tabliczki z twierdzeniami, czy problemami, możemy potraktować je jako pewien sposób zabawy matematyką.
Nie zawsze musimy się angażować w ich rozwiązywanie.
Zawsze możemy spróbować utworzyć konstrukcję z zagadnień umieszczonych na sangaku.
Pozwala to na łatwiejsze zrozumienie, nie tylko przykładu który konstruujemy, ale również możemy łatwiej pojąć inne, nawet szkolne zagadnienia z geometrii.
Istnieje wiele programów do tworzenia konstrukcji.Wystarczy tylko poszukać.
Chcąc zachęcić do takiego sposobu nauki matematyki, umieszczam dynamiczną kartę pracy z programu, którego używłam podczas tworzenia tej strony.
Sprawdź, czy masz dostęp do internetu, przed korzystaniem z umieszczonej karty pracy. Możesz spróbować stworzyć swoją konstrukcję, pobawić się kształtami i obiektami, lub skonstruować przykład z wybranego sangaku.
Wybór pozostawiam Tobie. Zachęcam do spróbowania i życzę miłej zabawy.