 Dla trójwymiarowej studni potencjału operator energii potencjalnej V(xi) dany jest formułą:
Dla trójwymiarowej studni potencjału operator energii potencjalnej V(xi) dany jest formułą:
Fizyka dla informatyków - Notatki w InternecieFizyka ciała stałego - zadania |
 Dla trójwymiarowej studni potencjału operator energii potencjalnej V(xi) dany jest formułą:
Dla trójwymiarowej studni potencjału operator energii potencjalnej V(xi) dany jest formułą:

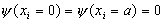 dla i = 1,2,3.
Znaleźć dopuszczalne wartości wektora falowego kn1, kn2, kn3 i energii En1n2n3 cząstki w studni.
dla i = 1,2,3.
Znaleźć dopuszczalne wartości wektora falowego kn1, kn2, kn3 i energii En1n2n3 cząstki w studni.
Rozwiązanie: Rozpatrujemy elektron w sześciennej studni potencjału o krawędzi a. Wówczas otrzymujemy równanie Schrödingera następującej postaci:Stosując metodę separacji zmiennych przedstawiamy funkcję falową w postaci iloczynu (1.1)
Zatem równanie pierwsze uzyskuje postać: Dzieląc obustronnie przez X(x)Y(y)Z(z) i rozdzielając względem pochodnych cząstkowych otrzymujemy trzy równania, których rozwiązania dają nam postać funkcji falowej. Przykładowo dla zmiennej x dostajemy: Konieczność zerowania się funkcji na granicach studni (0 i a) narzuca warunki na wartości kx: Stałą A dobieramy tak, aby funkcja była unormowana. Ostatecznie funkcja falowa jest postaci (po unormowaniu) Dzęki stałej k możemy uzyskać zalezność energii, która ma postać: 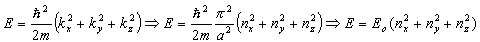
 Znależć zależność poziomu Fermiego w temperaturze zera bezwzględnego od gęstości elektronowej n:
Znależć zależność poziomu Fermiego w temperaturze zera bezwzględnego od gęstości elektronowej n:
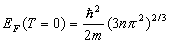 , oraz zależność średniej energii na elektron
od energii Fermiego
, oraz zależność średniej energii na elektron
od energii Fermiego 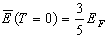 .
.
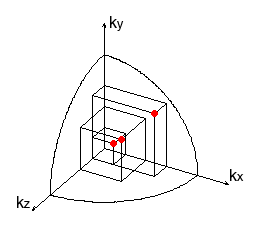
Rozwiązanie: Stany energetyczne o energii nie przekraczającej określonej wartości E można przedstawić jako punkty wewnątrz kuli w przestrzeni wektora falowego k. Promień tej kuli ma wartość k taką że:(2.1) Składowe wektora falowego k przyjmują wartości skwantowane:
Zatem w przestrzeni k, element o "objętości jednostkowej" równej
reprezentowany jest przez jeden dozwolony wektor k równy
aby otrzymać liczbę stanów dozwolonych wewnątrz kuli o promieniu k należy jej objętość podzielić przez
a potem pomnożyć przez 2 (gdyż oprócz trzech liczb kwantowych kx, ky, kz istnieje jeszcze spinowa liczba kwantowa ms przyjmująca dwie wartości). Liczba stanów dozwolonych wynosi więc:
(2.2) Stąd k jest równe:
gdzie n=N/V jest koncentracją elektronów w objętości próbki V. (2.3)
W temperaturze zera bezwzględnego wszystkie stany o energii mniejszej od pewnej wartości nazywanej energią Fermiego są zapełnione przez elektrony, natomiast stany o energii większej od energii Fermiego są nieobsadzone. Wstawiając równanie (2.3) do (2.1) otrzymujemy szukaną zależność energii Fermiego od koncentracji elektronów:Wstawiając równanie (2.1) do (2.2) otrzymujemy: (2.4)
Różniczkując (2.5) dostajemy wzór na liczbę stanów o energii zawartej w przedziale od E do E + dE: (2.5)
Możemy teraz obliczyć sumaryczną energię wszystkich elektronów w temperaturze zera bezwzględnego, równą: (2.6)
Średnią energię przypadającą na jeden elektron otrzymamy dzieląc sumaryczną energię elektronów (2.7) przez liczbę elektronów (2.5): (2.7)
(2.8)
 Proszę znaleźć gęstość stanów D(k) w przestrzeni wektora falowego i g(E) w przestrzeni energii dla cząstki w nieskończonej jedno-, dwu- i trzywymiarowej studni potencjału.
Proszę znaleźć gęstość stanów D(k) w przestrzeni wektora falowego i g(E) w przestrzeni energii dla cząstki w nieskończonej jedno-, dwu- i trzywymiarowej studni potencjału.
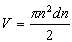
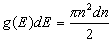

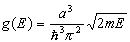
 Rozwiążmy równanie Schrödingera dla potencjału Kroniga-Penney'a (będącego przedstawionym na rysunku przybliżeniem potencjału rdzeni sieci krystalicznej) i energii cząstki E < E0
Rozwiążmy równanie Schrödingera dla potencjału Kroniga-Penney'a (będącego przedstawionym na rysunku przybliżeniem potencjału rdzeni sieci krystalicznej) i energii cząstki E < E0
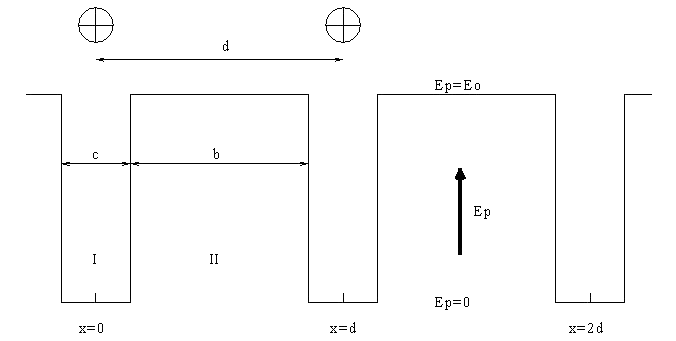
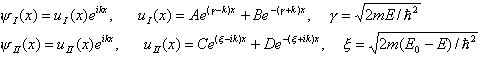
żądamy ciągłości funkcji falowej i jej pochodnej:
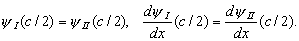
Warunek periodyczności rozwiązania (twierdzenie Blocha) narzuca kolejne dwa warunki:
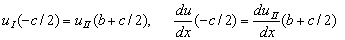
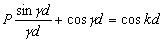
gdzie: 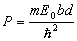
Równanie (4) można rozwiązać ze względu na E(k) numerycznie.
Jego prawa strona zmienia się w przedziale [-1,+1].
Wektor falowy k jest czysto urojony w przedziałach energii, gdzie lewa strona równania (4) jest większa od +1 lub mniejsza od -1.
Pęd cząstki musi być rzeczywisty, więc eletkron nie może mieć energii, dla których k jest urojone.
Prowadzi to do istnienia dozwolonych i wzbronionych pasm energii w ciałach stałych.
Wyznaczyć numerycznie zależność E(k).
Przyjąć 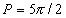 d = 2 A, m = me w przedziale energii od 0 eV do 200 eV.
Jak zmienia się szerokość pierwszego dozwolonego pasma w funkcji stałej sieci krystalicznej d (d = 1 A, d = 1,5 A, d = 2 A dla E0b = 25 eVA?
Jak zmienia się ta szerokość w funkcji E0 (E0 = 50 eVA, E0 = 75 eVA, E0b = 100 eVA dla d = 1 A)?
d = 2 A, m = me w przedziale energii od 0 eV do 200 eV.
Jak zmienia się szerokość pierwszego dozwolonego pasma w funkcji stałej sieci krystalicznej d (d = 1 A, d = 1,5 A, d = 2 A dla E0b = 25 eVA?
Jak zmienia się ta szerokość w funkcji E0 (E0 = 50 eVA, E0 = 75 eVA, E0b = 100 eVA dla d = 1 A)?
Rozwiązanie: Algorytm numerycznego rozwiązania równania:
- Ustaw E=0,
- Oblicz lewą stronę równania,
- Oblicz wartość wektora falowego jeżeli lewa strona równania zawiera się w przedziale <-1,1,
- Inkrementuj energię,
- Jeżeli E<200 eV to skocz do punktu 2,
 Pod wpływen zewnętrznego pola elektrycznego elektrony swobodne w metalach doznają przyśpieszenia zgodnie z prawami Newtona.
Jednak w obecności potencjału sieci krystalicznej zachowują się jakby były obdarzone efektywną masą m* różną od masy spoczynkowej m, i mogącą być zarówno większą od m (a nawet nieskończoną) lub mniejszą od m (a nawet ujemną), gdyż formalna definicja tego parametru związana jest z wypukłością związku dyspersyjnego E(k):
Pod wpływen zewnętrznego pola elektrycznego elektrony swobodne w metalach doznają przyśpieszenia zgodnie z prawami Newtona.
Jednak w obecności potencjału sieci krystalicznej zachowują się jakby były obdarzone efektywną masą m* różną od masy spoczynkowej m, i mogącą być zarówno większą od m (a nawet nieskończoną) lub mniejszą od m (a nawet ujemną), gdyż formalna definicja tego parametru związana jest z wypukłością związku dyspersyjnego E(k):
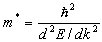
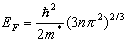 znaleźć masę efektywną elektronów walencyjnych w sodzie.
Sód jest jednowartościowy, jego masa atomowa wynosi 22.99 g/mol, zaś gęstość 0.97 g/cm3.
znaleźć masę efektywną elektronów walencyjnych w sodzie.
Sód jest jednowartościowy, jego masa atomowa wynosi 22.99 g/mol, zaś gęstość 0.97 g/cm3.Rozwiązanie: Dla elektronów swobodnych zależność między energią a wektorem falowym ma postać:Różniczkując ten wzór dwukrotnie otrzymujemy Następnie wstawiając to do wzoru na m* dostajemy m*=me. Dla elektronów znajdujących się w krysztale wzór na energię Fermiego wygląda następująco:
stąd
Należy zatem obliczyć koncentrację elektronów n=N/V, gdzie N jest liczbą elektronów walencyjnych, a V objętością próbki. Ponieważ sód jest jednowartościowy liczba elektronów walencyjnych równa jest liczbie atomów, a tą możemy obliczyć wykorzystując masę molową:
Energia Fermiego wynosi: EF=4ˇ10-19 [J]. Szukana masa efektywna jest równa: m*=1.1495ˇ10-30 [kg] (m*/me = 1.262)
Autorzy: Piotr Kopyt, Przemysław Musiał, Krzysztof Niemiec
 |
 |