 Trzy ładunki punktowe (+q, +q, -q) umieszczono w wierzchołkach trójkąta równobocznego.
Określić natężenie pola
Trzy ładunki punktowe (+q, +q, -q) umieszczono w wierzchołkach trójkąta równobocznego.
Określić natężenie pola 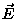 i potencjał V:
i potencjał V:
Fizyka dla informatyków - Notatki w InternecieElektromagnetyzm - zadania |
 Trzy ładunki punktowe (+q, +q, -q) umieszczono w wierzchołkach trójkąta równobocznego.
Określić natężenie pola
Trzy ładunki punktowe (+q, +q, -q) umieszczono w wierzchołkach trójkąta równobocznego.
Określić natężenie pola 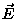 i potencjał V:
i potencjał V:
Rozwiązanie:
a)Z zasady superpozycji wiadomo, że , gdzie
są wektorami natężenia pochodzącymi od poszczególnych ładunków. Z prawa Culomba oraz definicji obliczamy poszczególne natężenia. Potencjał natomiast jest algebraiczną (tj. ze znakami) sumą wartości potencjałów pochodzących od poszczególnych ładunków.
W przypadku, gdy wszystkie ładunki są dodatnie mamy:
E = 0
b)
W przypadku, gdy badamy natężenie na boku trójkąta między ładunkami (+q) i (+q), wektory natężenia pochodzące od tych identycznych ładunków zniosą się. Pozostanie jedynie wektor natężenia pochodzący od ładunku (-q).
Zwrot tego wektora jest w kierunku ładunku (-q)
Potencjał:
W przypadku trzech jednakowych ładunków dodatnich, wartość natężenia wypadkowego nie zmieni się, zmieni się natomiast kierunek, tym razem zwrot w kierunku od ładunku (+q).
Zmieni się też potencjał:
 Znaleźć gradienty następujących pól:
Znaleźć gradienty następujących pól:
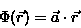
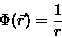
Rozwiązanie: W celu rozwiązania zadania należy zaznajomić się z kilkoma pojęciami:
Operator Hamiltona (nabla)jest to operator różniczkowy, który można formalnie traktować jako wektor.
Gradientem pola skalarnegonazywamy pole wektorowe
 Wyznaczyć natężenie pola
Wyznaczyć natężenie pola 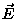 elektrostatycznego wytworzonego przez:
elektrostatycznego wytworzonego przez:
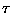
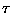 , a druga z gęstością -
, a druga z gęstością -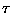
Rozwiązanie:a) Problem najłatwiej rozwiązać stosując prawo Gaussa. Za powierzchnię Gaussowską wybieramy walec o osi symetrii prostopadłej do powierzchni wytwarzającej pole. Mamy wówczas: gdzie: - względna przenikalność magnetyczna próżni,
- względna przenikalność magnetyczna materiału płyty,
- gęstość powierzchniowa ładunku,
- koło "wycięte" przez walec na płycie,
- powierzchnia walca.
Ponieważ całkowanie odbywa się po powierzchni zamkniętej, na całkę z lewej strony równania złożą się całki po pobocznicy i dwóch podstawach walca. Ponieważ jednak, wektor normalny pobocznicy jest równoległy do wektora natężenia, to ich iloczyn skalarny równy jest 0. W takim razie zostaje tylko całka po podstawach.
b) W tym przypadku, natężenia pól zsumują się między płaszczyznami, na zewnątrz natomiast się zniosą, gdyż wektory natężeń, pochodzące od obu płaszczyzn, mają te same wartości ale przeciwne zwroty. Mamy więc:
 Wyznaczyć potencjał V i natężenie pola elektrostatycznego
Wyznaczyć potencjał V i natężenie pola elektrostatycznego 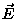 jako funkcję odległości od środka kuli o promieniu R, wewnątrz której znajduje się ładunek elektryczny rozłożony z gęstością objętościową spełniającą zależność
jako funkcję odległości od środka kuli o promieniu R, wewnątrz której znajduje się ładunek elektryczny rozłożony z gęstością objętościową spełniającą zależność  , gdzie
, gdzie 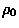 i a - stałe.
i a - stałe.
Rozwiązanie:
W celu wyliczenia natężenia i potencjału V należy rozpatrzyć 2 przypadki:
UWAGA! Należy tak dobrać stałe całkowania aby potencjał był ciągły!
- r<R
policzymy z prawa Gaussa, za powierzchnie gaussowskie wybierając sfery o środku w środku kuli. Aby wyznaczyć ładunek wewnątrz takiej sfery o priomieniu r musimy ją podzielić na bardzo cienkie sfery o grubości dr: element objetości d
obliczymy jako różnicę objętości 2 kul: o promieniach r i (r+dr). Wewnatrz sfery o promieniu r
Natomiast V znajdujemy z zależności:
- r>=R
Całkowity ładunek zgromadzony w kuli wyraża się wzorem:
i w miarę zwiększania promieni sfer gaussowskich nie ulega już zmianie. Natężenie i potencjał z tych samych zależnosci jak dla r<R.
 Wyznaczyć potencjał V i natężenie pola elektrostatycznego
Wyznaczyć potencjał V i natężenie pola elektrostatycznego 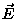 naładowanej, nieskończenie długiej, prostoliniowej, metalowej nici.
Wykreślić jako funkcję odległości od osi nici wartości obu tych wielkości.
Przyjąć, że gęstość liniowa ładunku na nici jest stała i równa
naładowanej, nieskończenie długiej, prostoliniowej, metalowej nici.
Wykreślić jako funkcję odległości od osi nici wartości obu tych wielkości.
Przyjąć, że gęstość liniowa ładunku na nici jest stała i równa 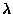 .
.
Rozwiązanie:
Znów skorzystamy z prawa Gaussa.Ze względu na symetrię problemu jako powierzchnię gaussowską wybieramy powierzchnię walca o promieniu r. Pole wytworzone przez nić musi być ze względu na symetrię zagadnienia polem wektorowym osiowym. Na powierzchni bocznej walca wartość E jest więc stała. Należy zauważyć, że wartość strumienia E przez podstawy walca jest równa 0. Wartość potencjału V wyliczamy w oparciu o wyliczone wcześniej E korzystając z wzoru
Ostatecznie
 Sformułować i przedyskutować równania Maxwella.
Jakie wnioski dotyczące tych pól wynikają z otrzymanych równań gdy:
Sformułować i przedyskutować równania Maxwella.
Jakie wnioski dotyczące tych pól wynikają z otrzymanych równań gdy:
Rozwiązanie: Równania Maxwella w postaci całkowej i różniczkowej
Z postaci całkowej w różniczkową przechodzimy dzięki poniższym twierdzeniom:Przykład przejścia z postaci całkowej na różniczkową dla prawa Gaussa dla pola elektrycznego:
- Gaussa-Ostrogradskiego:
- Stokesa:
Ponieważ powyższe równanie musi być słuszne dla dowolnej objętości V - muszą być równe funkcje podcałkowe, tzn.
 Korzystając z równań Maxwella oraz tożsamości
Korzystając z równań Maxwella oraz tożsamości
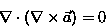
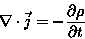
Rozwiązanie:
Z praw Maxwella wiemy, że:Działając na to równanie obustronnie operatorem nabla otrzymujemy: skąd przy (także z praw Maxwella): po podstawieniu otrzymujemy:
 Jaką siłą działają na siebie dwa równoległe przewodniki o długości l umieszczone w odległości a, przez które płyną prądy o natężeniach I1 i I2?
Na podstawie wyniku sformułować definicję ampera absolutnego.
Jaką siłą działają na siebie dwa równoległe przewodniki o długości l umieszczone w odległości a, przez które płyną prądy o natężeniach I1 i I2?
Na podstawie wyniku sformułować definicję ampera absolutnego.
Rozwiązanie:Korzystając z prawa Ampera, znajdujemy natężenie pola magnetycznego pochodzącego od przewodu (1) w odległości a od przewodu:
Ponieważ przewodnik (2) umieszczony jest w polu przewodu (1), więc działa na niego siła elektrodynamiczna: Przyjmując teraz: a=1m, I1=I2=1A otrzymujemy wartość siły, przypadającej na jednostkę długości, z jaką przyciągać się przewodniki oddalone o jednostkową odległość, w których płyną prądy o jednostkowych natężeniach: F=2 10-7 N.
 W polu długiego przewodu, w którym płynie prąd I1 znajduje się ramka prostokątna o wymiarach axb, przez którą płynie prąd I2.
Odłegłość osi symetrii ramki od przewodu wynosi c.
Obliczyć siłę i moment siły działający na ramkę gdy:
W polu długiego przewodu, w którym płynie prąd I1 znajduje się ramka prostokątna o wymiarach axb, przez którą płynie prąd I2.
Odłegłość osi symetrii ramki od przewodu wynosi c.
Obliczyć siłę i moment siły działający na ramkę gdy:
a)Siła elektrodynamiczna działająca na elementy ramki wynosi dla każdego boku, przy czym siły działające na boki a ramki równoważą się i do siły wypadkowej nic nie wnoszą. Wartości indukcji B1 i B2 pochodzą od przewodnika z prądem I1 a zależą od odległości boku ramki od tego przewodnika. Aby znaleźć te wielkości korzystamy z prawa Ampera.
Ostatecznie:
Natomiast wypadkowy moment działający na ramkę równy jest 0.
b)
Siła elektrodynamiczna działająca na boki ramki o długości a w tym wypadku też będzie równa zero, a siły działająca na boki ramki o długości b są równe co do wartoci. Siła ta wynosi:
Siłę wypadkową najlepiej jest obliczać z twierdzenia cosinusów. Po prostych obliczeniach otrzymujemy, że:
W obliczeniach momentu działającego na ramkę, należy zwrócić uwagę na zależnoci trygonometryczne na rysunku.
 Korzystając z prawa Ampera oraz Biota-Savarta-Laplace'a wyznaczyć wartość natężenia pola magnetycznego w punkcie P na rysunku poniżej.
Dane jest natężenie prądu I oraz promień pętli R.
Korzystając z prawa Ampera oraz Biota-Savarta-Laplace'a wyznaczyć wartość natężenia pola magnetycznego w punkcie P na rysunku poniżej.
Dane jest natężenie prądu I oraz promień pętli R.

Rozwiązanie:
Do rozwiązania zadania wykorzystamy prawo Ampera oraz prawo Biota-Savarta-Laplace'a. Wartość natężenia pola magnetycznego H w punkcie P najlepiej wyznaczyć jako sumę dwóch natężeń H1+H2, gdzie H1 to wartość natężenia pola magnetycznego w odległości R od nieskończenie długiego prostoliniowego przewodnika,zaś H2 to wartość natężenia pola magnetycznego w środku pierścienia o promieniu R, Wartość H1 obliczamy korzystając z prawa Ampera. Podczas obliczeń warto zauważyć, że H1 można wyłączyć przed znak całki. Wartość H2 obliczamy korzystając z prawa Biota-Savarta-Laplace'a. Po wyliczeniu wartości indukcji magnetycznej korzystając z zależności wyliczamy wartość H2.
Odpowiedź:
 Znaleźć ruch przewodnika spadającego w polu grawitacyjnym wzdłuż pary przewodów zwartych oporem R.
Masa poprzeczki m, długość poprzeczki l, opór poprzeczki i przewodów jest zaniedbywalny w porównaniu z oporem R.
Prostopadle do płaszczyzny przewodów działa stałe pole magnetyczne o indukcji B.
Prędkość początkowa poprzeczki vO=0.
Znaleźć ruch przewodnika spadającego w polu grawitacyjnym wzdłuż pary przewodów zwartych oporem R.
Masa poprzeczki m, długość poprzeczki l, opór poprzeczki i przewodów jest zaniedbywalny w porównaniu z oporem R.
Prostopadle do płaszczyzny przewodów działa stałe pole magnetyczne o indukcji B.
Prędkość początkowa poprzeczki vO=0.
Rozwiązanie:Rozwiązując zadanie należy skorzystać z prawa indukcji Faraday'a oraz prawa Ohma.
Na początku, gdy prędkość poprzeczki v0=0 jedyną siłą działającą na poprzeczkę jest siła ciężkości Q=mg. Należy zauważyć, że poprzeczka spadając powoduje zmianę wartości strumienia indukcji magnetycznej
(bo zmienia się wartość powierzchni przez którą przenika pole). Na skutek zmiany wartości strumienia w obwodzie pojawia się prąd indukcyjny.
Wówczas na ramkę zaczyna działać siła elektrodynamiczna. Siła elektrodynamiczna to siła, która działa na przewodnik z prądem umieszczony w polu magnetycznym a jej wartość liczymy ze wzoru .
Kierunek i zwrot siły wyznaczamy z reguły trzech palców lewej dłoni. Kierunek tej siły jest taki sam jak siły ciężkości Q, lecz zwroty tych sił są przeciwne. Wypadkowa siła działająca na poprzeczkę jest różnicą siły ciężkości i siły elektrodynamicznej. Aby wyliczyć zależności x(t), należy najpierw rozwiązać równanie różniczkowe niejednorodne pierwszego rzędu, w którym niewiadpmą jest prędkość v, a następnie obustronnie całkując otrzymamy zależność x(t). Stałą całkowania wyliczamy w oparciu o warunki początkowe: x(0)=0.
Autorzy: Szymon Nocoń, Piotr Nowak, Dariusz Kościelniak, Michał Kułakowski
 |
 |