 Korzystając z postulatów Bohra znaleźć poziomy energii jonów wodoropodobnych:
Korzystając z postulatów Bohra znaleźć poziomy energii jonów wodoropodobnych: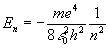
wskazówka
Fizyka dla informatyków - Notatki w InternecieMechanika kwantowa - zadania |
 Korzystając z postulatów Bohra znaleźć poziomy energii jonów wodoropodobnych:
Korzystając z postulatów Bohra znaleźć poziomy energii jonów wodoropodobnych:
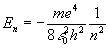
wskazówka
 Sprawdzić równania operatorowe:
Sprawdzić równania operatorowe:
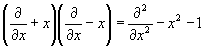
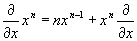
 Korzystając z przedstawienia Jordana
Korzystając z przedstawienia Jordana
 znaleźć operatory:
znaleźć operatory:
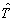 dla cząstki swobodnej,
dla cząstki swobodnej,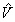 oscylatora harmonicznego,
oscylatora harmonicznego,
 Wykazać, że u(x) = exp (-x2/2) jest funkcją własną operatora d2/dx2-x2 i znaleźć wartość własną dla tego operatora odpowiadającą wektorowi u(x).
Odpowiednikiem jakiej klasycznej wielkości może być operator
Wykazać, że u(x) = exp (-x2/2) jest funkcją własną operatora d2/dx2-x2 i znaleźć wartość własną dla tego operatora odpowiadającą wektorowi u(x).
Odpowiednikiem jakiej klasycznej wielkości może być operator 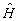 ?
?
wskazówka
 Korzystając z przedstawienia Jordana zapisać równanie operatorowe
Korzystając z przedstawienia Jordana zapisać równanie operatorowe 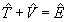 , gdzie
, gdzie
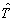 - operator energii kinetycznej,
- operator energii kinetycznej,
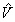 - operator energii potencjalnej,
- operator energii potencjalnej,
 - operator energii całkowitej.
(po dołożeniu za operatorami funkcji falowej Y(x,t) jest to równanie Schrödingera z czasem).
Następnie zakładając niezależność energii potencjalnej od czasu
- operator energii całkowitej.
(po dołożeniu za operatorami funkcji falowej Y(x,t) jest to równanie Schrödingera z czasem).
Następnie zakładając niezależność energii potencjalnej od czasu 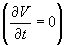 oraz stosując metodę rozdzielenia zmiennych (wzór)
oraz stosując metodę rozdzielenia zmiennych (wzór) 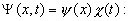


 Pokazać, że dla cząstki swobodnej funkcja falowa
Pokazać, że dla cząstki swobodnej funkcja falowa 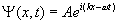 spełnia równanie (falowe) Schrödingera (z czasem).
spełnia równanie (falowe) Schrödingera (z czasem).
wskazówka
 Wartość średnią dowolnego operatora
Wartość średnią dowolnego operatora  dla układu znajdującego się w stanie opisanym unormowaną funkcją falową
dla układu znajdującego się w stanie opisanym unormowaną funkcją falową 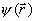 liczymy jako:
liczymy jako: 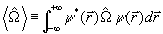 .
Znaleźć średnią energię kinetyczną w stanie
.
Znaleźć średnią energię kinetyczną w stanie 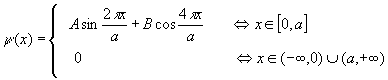 >w układzie jednowymiarowym.
>w układzie jednowymiarowym.
wskazówka
 Dla jednowymiarowej nieskończonej studni potencjału operator energii potencjalnej V(x) dany jest formułą:
Dla jednowymiarowej nieskończonej studni potencjału operator energii potencjalnej V(x) dany jest formułą:
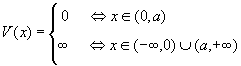
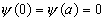 .
Znaleźć dopuszczalne wartości energii cząstki w studni.
.
Znaleźć dopuszczalne wartości energii cząstki w studni.
 Cząstka o energii E<V0 opisana falą płaską wzór nadchodząca z lewej strony zderza się ze skokiem potencjału:
Cząstka o energii E<V0 opisana falą płaską wzór nadchodząca z lewej strony zderza się ze skokiem potencjału:

 Nieunormowana funkcja falowa cząstki swobodnej poruszającej się po linii prostej dana jest formułą:
Nieunormowana funkcja falowa cząstki swobodnej poruszającej się po linii prostej dana jest formułą:
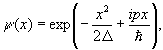
 są stałe.
Znaleźć średnią wartość położenia
są stałe.
Znaleźć średnią wartość położenia 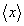 i pędu
i pędu 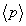 cząstki w tym stanie.
cząstki w tym stanie.
 W wyniku zderzenia fotonu o długości fali l0 z elektronem swobodnym (lub słabo związanym) następuje rozproszenie fotonu (tzw. rozpraszanie comptonowskie), któremu towarzyszy zmiana długości fali fotonu (l0 --> l) oraz kierunku o kąt
W wyniku zderzenia fotonu o długości fali l0 z elektronem swobodnym (lub słabo związanym) następuje rozproszenie fotonu (tzw. rozpraszanie comptonowskie), któremu towarzyszy zmiana długości fali fotonu (l0 --> l) oraz kierunku o kąt 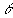 .
Korzystając z praw zachowania energii i pędu wyprowadzić wzór na comptonowską zmianę długości fali.
.
Korzystając z praw zachowania energii i pędu wyprowadzić wzór na comptonowską zmianę długości fali.
Prawo zachowania pędu najwygodniej zapisać korzystając z twierdzenia cosinusów: ![]() ,
,
do prawa zachowania energii energie elektronu najlepiej liczyć z niezmiennika relatywistycznego: ![]() .
.
wskazówka
Autorzy: Artur Dragan, Artur Majka, Konrad Kozikowski
 |
 |