 Publikacja została dofinansowana z programu ,,Doskonała Nauka” Ministerstwa Edukacji i Nauki (nr wniosku: DNM/SP/514772/2021)
Publikacja została dofinansowana z programu ,,Doskonała Nauka” Ministerstwa Edukacji i Nauki (nr wniosku: DNM/SP/514772/2021)
AGH, Akademia Górniczo-Hutnicza,
Wydział Inżynierii Materiałowej i Ceramiki,
Katedra Ceramiki i Materiałów Ogniotrwałych
Wersja online
Lipiec 2022, (w. 1.02)
 Publikacja została dofinansowana z programu ,,Doskonała Nauka” Ministerstwa Edukacji i Nauki (nr wniosku: DNM/SP/514772/2021)
Publikacja została dofinansowana z programu ,,Doskonała Nauka” Ministerstwa Edukacji i Nauki (nr wniosku: DNM/SP/514772/2021)
 Ten utwór jest dostępny na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 4.0 Międzynarodowe.
Ten utwór jest dostępny na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 4.0 Międzynarodowe.
Treść licencji dostępna jest na stronie internetowej
CreativeCommons.org pod adresem: https://creativecommons.org/licenses/by-sa/4.0/legalcode.pl
Strona ta zawiera pełną treść monografii, wydanej w roku 2022 w Wydawnictwie Naukowym AKAPIT, pod tytułem: ,,Mikrostruktura jako podstawa modelowania numerycznego właściwości tworzyw ceramicznych”. Publikacja monografii, zarówno w wersji drukowanej jak i elektronicznej, została dofinansowana przez Ministerstwo Edukacji i Nauki z programu Doskonała Nauka.
Zawarty tutaj materiał dostępny jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 4.0 Międzynarodowe. Oznacza to, że możesz go kopiować, zmieniać, rozpowszechniać w dowolnym medium i formacie, jednak uszanuj moją pracę i oznacz moje autorstwo (pełna treść licencji CC BY-SA 4.0 dostępna jest na stronie Creative Commons). Aby ułatwić Ci cytowanie, przygotowałem gotowe pliki w popularnych formatach: BibTeX, Ris, EndNote i w pliku tekstowym.
Chciałbym też zaznaczyć, że konwersja drukowanej książki na wersję internetową, może nie być idealna i publikacje te mogą nieznacznie się różnić. Jeśli więc zależy Ci na jak największej zgodności z wydanym oryginałem, to możesz pobrać monografię w formacie pdf. Jeśli natomiast wolisz lekturę na ekranie czytnika e-booków, to przygotowałem wersję epub.
Będę również wdzięczy za wszelkie uwagi i komentarze dotyczące treści zawartych w monografii, tym bardziej jeśli podczas korekty przeoczyłem jakieś błędy, za które z góry przepraszam. W tych i innych kwestiach, proszę zatem pisać na mój adres e-mail: grzegorz.grabowski@agh.edu.pl.
Podstawą do przygotowania tego opracowania stały się notatki zebrane przeze mnie w ciągu kilkunastu lat, podczas których zajmowałem się modelowaniem budowy i właściwości tworzyw ceramicznych. Dotyczyły one stosowanych w tym obszarze koncepcji i praktycznych rozwiązań, a ich źródłem były publikacje naukowe, na których opierałem się w swoich pracach. Na potrzeby tego opracowania, notatki te usystematyzowałem i rozszerzyłem, a dodatkowo dołączyłem do nich własne rozwiązania, które powstawały w kolejnych realizowanych pracach badawczych. Ponadto, aby ukazać szersze tło i umiejscowić stosowane techniki w przestrzeni badawczej zajmowanej aktualnie przez inżynierię materiałową, dodałem również informacje o innych metodach, które w moim odczuciu mogą być istotne dla dalszego rozwoju tej dziedziny wiedzy. Dobór przestawionych tutaj zagadnień, został jednak ograniczony jedynie do tych, które znajdują zastosowanie w pracach naukowo-badawczych prowadzonych nad materiałami ceramicznymi.
Głównym celem tej pracy, było więc zebranie i usystematyzowanie informacji na temat modelowania numerycznego budowy wewnętrznej i właściwości polikrystalicznych tworzyw ceramicznych. Użyty przeze mnie tytuł: ,,Mikrostruktura jako podstawa modelowania numerycznego właściwości tworzyw ceramicznych”, jest jednak skrótem, bo w istocie, opisane zagadnienia dotyczą głównie cech materiałów posiadających niejednorodną budowę wewnętrzną, określaną mianem mikrostruktury. Zatem w odniesieniu do ceramicznych materiałów amorficznych, przedstawione zależności i metody, nie będą miały szerszego zastosowania. Jednak nie wyklucza to możliwości wykorzystania ich do analizowania właściwości materiałów wielofazowych, w których faza amorficzna stanowi jeden ze składników budowy wewnętrznej.
Zebrany tutaj materiał może posłużyć zarówno jako wprowadzenie do tematyki dotyczącej opisu i modelowania właściwości ceramicznych materiałów polikrystalicznych, ale także może pozwolić na realizację zaawansowanych modeli umożliwiających symulacje w zakresie właściwości termosprężystych. Użyteczność przedstawionych tu rozwiązań została potwierdzona szeregiem publikacji, dlatego mogą one stanowić nie tylko punkt wyjścia do dalszych badań podstawowych, ale mogą również posłużyć do ilościowych analiz inżynierskich.
Układ i zakres treści zawartych w tym opracowaniu, został dostosowany do wspomnianego celu. W rozdziale 1. zawarte są więc zagadnienia dotyczące wybranych właściwości termomechanicznych. Zostały one ujęte w zakresie podstawowym tak, aby podkreślić specyfikę opisu wykorzystywanego dla materiałów ceramicznych. Przedstawione informacje o właściwościach sprężystych, wytrzymałości, kruchości czy rozszerzalności cieplnej, zostały skonfrontowane z cechami mikrostruktury. W moim odczuciu, takie połączenie może być kluczowe dla zrozumienia właściwości rozpatrywanej grupy tworzyw inżynierskich. Dodatkowo w rozdziale tym opisane zostały resztkowe naprężenia cieplne. Naprężenia te nie są oczywiście właściwością sensu stricto, jednak ich obecność w materiałach ceramicznych jest nieunikniona i w wielu przypadkach istotnie modyfikuje makroskopowe cechy materiałów należących tej grupy tworzyw. Dlatego ujęcie tego zjawiska już w części wprowadzającej, podkreśla jego istotne znaczenie dla zrozumienia specyfiki polikrystalicznych materiałów ceramicznych.
W rozdziale 2. zostały opisane metody i techniki służące do badania i analizy budowy wewnętrznej materiałów. Tutaj również wybór przedstawionych treści opierał się zarówno na szerokim przeglądzie publikacji z zakresu metod obrazowania i rekonstrukcji mikrostruktury, jak i na doświadczeniach własnych. Specyfika budowy, dotycząca niewielkiego rozmiaru elementów mikrostrukturalnych, trudności w przygotowaniu próbek oraz ograniczenia natury fizykochemicznej, sprawiają, że tylko niektóre z aktualnie rozwijanych metod mogą zostać wykorzystane w badaniach budowy wewnętrznej materiałów ceramicznych. Ostatecznie, przedstawione w tym rozdziale koncepcje, zostały więc ograniczone jedynie do tych, które znajdują, albo potencjalnie mogą znaleźć, zastosowanie do opisu mikrostruktury tej grupy tworzyw.
Rozdział 3. poświęcony został już bezpośrednio metodom obliczeniowym. Dobór zawartych w tym rozdziale zagadnień, miał na celu przybliżenie fundamentalnych pojęć oraz najważniejszych koncepcji i zilustrowanie głównych kierunków, aktualnie prowadzonych badań w zakresie modelowania numerycznego właściwości tworzyw niejednorodnych, opartego na cyfrowej reprezentacji mikrostruktury. W rozdziale tym uwzględniony został również problem reprezentatywności. Ma on szczególne znaczenie podczas analiz ilościowych, służących do symulacji makroskopowych właściwości materiału. Dodatkowo opisana została tutaj również koncepcja wirtualnego laboratorium, której elementy zaczynają coraz częściej pojawiać się w pracach badawczych, i która może doprowadzić do znaczącego postępu w dziedzinie projektowania i optymalizacji właściwości tworzyw.
W ostatnim rozdziale przedstawione zostały przykłady analiz, przeprowadzonych metodą elementów skończonych, na podstawie syntetycznych oraz zrekonstruowanych modeli mikrostruktury materiałów ceramicznych. Zawarty w tej części opis gotowych rozwiązań, które były wykorzystywane wcześniej w pracach własnych, może być ilustracją i uzupełnieniem treści ujętych w trzech pierwszych rozdziałach. Przedstawione w rozdziale 4. techniki, narzędzia i wybrane modele, mogą również stanowić bazę do rozwiązywania praktycznych problemów badawczych i inżynierskich, prowadzonych z wykorzystaniem symulacji numerycznych. Dlatego też sposób prezentacji zawartych w tym rozdziale treści, został nakierowany głównie na przybliżenie możliwych do zastosowania technik, a nie na opis konkretnych wyników, które były uzyskiwane dla analizowanych materiałów, i które są zawarte w cytowanych pracach.
Wyjaśnienia może wymagać również rozmiar załączonej na końcu bibliografii. Jej liczebność wynika z szerokiego zakresu zagadnień poruszanych w kolejnych rozdziałach. Przedstawione w nich kierunki badań, mające na celu coraz lepszy opis budowy i właściwości materiałów, są efektem ciągłego rozwoju inżynierii materiałowej. Interdyscyplinarne podejście, łączące w sobie elementy klasycznych pomiarów doświadczalnych, nowoczesnych technik obrazowania i metod symulacyjnych, jest coraz częściej niezbędne do opracowania nowych tworzyw, czy lepszego zrozumienia zjawisk rządzących zachowaniem materiału w makroskali. Dlatego próba ujęcia tak rozległego zakresu tematycznego, i tak ograniczona jedynie do wybranych właściwości polikrystalicznych materiałów ceramicznych, wymagała poruszenia wielu zagadnień należących do różnych obszarów badawczych. Dlatego zebrana w bibliografii obszerna baza literaturowa, która oczywiście nie stanowi kompletnego zestawienia, może być jedynie wskazówką, co do kierunków dalszych dociekań.
Wykorzystane do zilustrowania opisywanych zagadnień rysunki, diagramy, wykresy i tabele, zostały przygotowane w oparciu o wyniki prac własnych oraz na podstawie zebranych danych albo ilustracji, pochodzących z prac opublikowanych przez innych autorów. W takim przypadku, w stosownych miejscach, załączone zostały informacje o źródle danych, jego autorze i wykorzystanej pracy.
Zdaje sobie sprawę, że przedstawione tutaj zagadnienia dotyczące modelowania polikrystalicznych tworzyw ceramicznych, są jedynie zarysem problematyki z jaką można się spotkać podczas prac realizowanych metodami numerycznymi w celu poznania związków między budową a właściwościami tworzyw. Mam jednak nadzieję, że sposób w jaki zostały one tutaj zaprezentowane, będzie dla czytelnika przydatny i pomoże mu w poszerzeniu wiedzy o tym ciekawym i szybko rozwijającym się obszarze badań.
Grzegorz Grabowski
Kraków, listopad 2020
Dążenie do dogłębnego poznania relacji występujących pomiędzy wewnętrzną budową materiałów a ich makroskopowymi właściwościami, leży u podstaw nauki o materiałach. Związek ten, stał się więc jednym z głównych paradygmatów inżynierii materiałowej. Coraz lepsze zrozumienie oddziaływań istniejących na różnych poziomach budowy, począwszy od struktury atomowej, przez mikrostrukturę, aż do budowy zewnętrznej ciał, oraz zależności występujących pomiędzy tymi poziomami, pozwoliło na znaczący postęp w zakresie projektowania, syntezy i modyfikacji właściwości tworzyw. W materiałach wielofazowych lub polikrystalicznych, w których wyróżnić można mikrostrukturę, jako jeden z elementów budowy wewnętrznej, jej rola jest złożona. Z jednej strony pośredniczy ona w przekazywaniu fundamentalnych oddziaływań międzyatomowych i w specyficzny sposób agreguje je, co w efekcie istotnie wpływa na właściwości makroskopowe materiału. Z drugiej strony, mikrostruktura pełni również rolę w procesie odwrotnym; rozdziela i przenosi zewnętrzne oddziaływania fizykochemiczne, wynikające z interakcji ciała z otoczeniem, z powrotem, na poziom podstawowy, uruchamiając tym samym ponownie zjawiska w skali atomowej. Takie pośredniczenie między oddziaływaniami występującymi na różnych poziomach, sprawia, że nawet niewielkie zmiany budowy mikrostruktury mogą prowadzić do dużych zmian we właściwościach makroskopowych materiału. Co również istotne, modyfikacja mikrostruktury może być przeprowadzona niekiedy, bez konieczności znaczącej ingerencji w skład chemiczny tworzywa – jedynie poprzez przemiany fizyczne zachodzące w trakcie jego otrzymywania. Dlatego też, mikrostruktura od dawna stanowi poziom budowy materiału, który skupia na sobie zainteresowania badawcze.
Wiele spośród znanych już dzisiaj związków między mikrostrukturą a właściwościami materiału, zostało sformułowanych w oparciu o informacje uzyskane jedynie na podstawie wyników obserwacji przełomów lub płaskich przekrojów. Rozwój metod obrazowania, który pod koniec zeszłego stulecia doprowadził do powstania narzędzi pozwalających na prowadzenie trójwymiarowych obserwacji budowy wewnętrznej materiału, sprawił jednak, że aktualnie prowadzone badania mogą opierać się już na danych doświadczalnych opisujących przestrzenne cechy i związki występujące w materiale. Takie przejście od badań opartych na informacjach uzyskanych z dwuwymiarowych przekrojów czy przełomów do analiz wykorzystujących pełną, trójwymiarową charakterystykę budowy wewnętrznej, stanowiło nie tylko zmianę jakościową, ale również ilościową. Informacje o parametrach topologicznych i morfologicznych, które jeszcze do niedawna były niedostępne albo mogły zostać jedynie oszacowane, obecnie są już wyznaczane bezpośrednio. Taka zmiana w sposobie opisu budowy materiału wymaga jednak użycia nowych narzędzi. Nieprzypadkowo więc rozwój metod wykorzystywanych do trójwymiarowego obrazowania, związany jest z rozwojem technik komputerowych i oprogramowania, służących do przetwarzania i analizy danych pomiarowych. Dzisiaj, praktycznie wszystkie zaawansowane metody wykorzystywane do obserwacji budowy wewnętrznej materiału, wymagają przetworzenia ogromnych ilości danych pomiarowych. Dopiero po usystematyzowaniu i integracji zebranych danych, możliwe jest uzyskanie wartościowych wyników, chociażby w postaci trójwymiarowych cyfrowych rekonstrukcji mikrostruktury.
Na zmianę w sposobie obserwacji materiału nałożyła się również zmiana w metodach wykorzystywanych do opisu relacji istniejących między mikrostrukturą a właściwościami. Proste empiryczne zależności, oparte na zwięzłych analitycznych równaniach, stopniowo przerodziły się w coraz bardziej złożone fenomenologiczne związki, których celem było całościowe ujęcie zjawisk obserwowanych w rzeczywistych materiałach. Poziom złożoności równań, konstruowanych na podstawie takich związków, dla wielu zagadnień uniemożliwił jednak uzyskanie analitycznych rozwiązań. Dlatego w inżynierii materiałowej, do badania tak sformułowanych problemów, zastosowane zostały metody numeryczne.
Stochastyczna natura wielu zjawisk zachodzących w materiale, wprowadza dodatkowe komplikacje w jego opisie. Jeden ze sposobów ujęcia takiego charakteru rzeczywistych tworzyw, opiera się na wykorzystaniu w modelach numerycznych, cyfrowych reprezentacji mikrostruktury. Pozwala to na uwzględnienie zróżnicowania cech morfologicznych i topologicznych oraz losowości analizowanych zjawisk, wywołanych lokalnymi konfiguracjami niejednorodności budowy i właściwości. Podejście to, będące głównym przedmiotem tego opracowania, wymaga jednak połączenia ze sobą realistycznego opisu budowy wewnętrznej, oddającego w sposób reprezentatywny różnorodność cech mikrostruktury, z równaniami konstytutywnymi, zapewniającymi precyzyjny opis właściwości na różnych poziomach budowy materiału.
Te dwa elementy, decydujące o jakości prowadzonych analiz numerycznych, są jednak specyficzne dla rozpatrywanych grup materiałów. Niektóre wymagania, niezbędne do precyzyjnego opisu zachowania materiałów polimerowych czy metalicznych, mogą w przypadku materiałów ceramicznych zostać znacząco uproszczone bądź nawet całkowicie pominięte. Z kolei inne, dla materiałów kowalencyjno-jonowych, nabierają szczególnego znaczenia. Dlatego w kolejnych rozdziałach zostaną omówione wybrane właściwości, metody badań oraz modele mikromechaniczne, pozwalające na jakościowy i ilościowy opis cech charakterystycznych dla ceramicznych materiałów polikrystalicznych.
Tworzywa ceramiczne, będące nieorganicznymi materiałami niemetalicznymi, stanowią, obok materiałów polimerowych i metalicznych, jedną z trzech grup materiałów inżynierskich. Dominujący udział wiązania kowalencyjnego lub jonowego, sprawia, że materiały ceramiczne posiadają specyficzne właściwości fizykochemiczne: wysoką temperaturę topnienia, stabilność chemiczną, dużą sztywność, wytrzymałość oraz twardość, odporność na pełzanie jak również odporność cieplną, dzięki którym są tradycyjnie wykorzystywane w roli materiałów konstrukcyjnych. Wysokie wymagania dotyczące właściwości oraz niezawodności nowoczesnych tworzyw, wymuszają intensywną kontrolę procesu technologicznego, zarówno w zakresie parametrów syntezy, jak również składu surowcowego. Dlatego zaawansowane tworzywa ceramiczne otrzymywane są aktualnie z wysoko przetworzonych surowców o ściśle określonym składzie – najczęściej surowców syntetycznych: pierwiastków i związków chemicznych. Materiały takie, obok ceramiki tradycyjnej, stanowią dużą grupę tworzyw zaliczanych do ceramiki specjalnej. Są to materiały węglikowe [1–3], tlenkowe [4–6], azotkowe [7, 8] oraz borkowe [9, 10], posiadające polikrystaliczną mikrostrukturę, która w istotny sposób wpływa na ich właściwości. Modyfikacja składu, prowadzona poprzez celowe zestawienie różnych faz ceramicznych, pozwala również na wytworzenie kompozytów, które łączą w sobie najbardziej pożądane cechy składników, a niejednokrotnie, poprzez synergię, uzyskują nowe, unikalne właściwości, nieobecne w jednofazowych spiekach [11].
Mikrostruktura zaawansowanych materiałów ceramicznych, rozumiana jako niejednorodność budowy i składu, jest kształtowana w trakcie procesu wysokotemperaturowej syntezy. Ewolucję mikrostruktury, determinują więc zarówno właściwości faz składowych: skład chemiczny, właściwości cieplne, elektryczne, magnetyczne, budowa krystaliczna, orientacja przestrzenna krystalitów, aglomeratów czy wtrąceń, ale również czynniki zewnętrzne: ciśnienie, temperatura i czas trwania procesu (historia cieplna) oraz skład atmosfery reakcyjnej [5, 12–15]. W efekcie, obecne w materiałach ceramicznych mikrostruktury mogą wykazywać duże zróżnicowanie morfologiczne i topologiczne.
Nawet w najprostszym układzie – nieporowatym, jednofazowym polikrysztale – możemy obserwować zarówno regularny pokrój krystalitów o zbliżonych wymiarach, które modelowo przybliżyć można czternastościanami Kelvina [16], jak również struktury składające się z ziaren 1 o zróżnicowanych wymiarach i kształtach (rys. 1.1 a–c). W materiałach wielofazowych, z uwagi na różnice w składzie chemicznym ziaren, a tym samym ich strukturze krystalicznej, zróżnicowanie morfologiczne jest na ogół jeszcze większe – szczególnie, gdy wysokotemperaturowa synteza przebiega w obecności fazy ciekłej, która lokując się w granicach międzyziarnowych, istotnie wpływa na ostateczny kształt krystalitów (rys. 1.1 d).
Materiały kompozytowe, składające się z ceramicznej osnowy, w której zdyspergowana jest ceramiczna faza wzmacniająca, przyjmująca postać: cząstek, wiskerów lub włókien, dziedziczą wymienione cechy morfologiczne. Dodatkowo, wtrącenia mogą wykazywać różny stopień ujednorodnienia w osnowie, a w skrajnym przypadku, mogą tworzyć aglomeraty. Dla wydłużonych wtrąceń (wiskerów oraz włókien), istotna staje się również ich wzajemna orientacja. Można zatem zauważyć zarówno przypadkowe ich ułożenie, jak również obserwować tendencję do przyjmowania wybranej orientacji przestrzennej.
Swoją specyfikę w budowie wewnętrznej posiadają również kompozyty, w których przekroczony został próg perkolacji [17–20]. Składają się one najczęściej z dwóch, a niekiedy trzech, ciągłych w przestrzeni faz, które tworzą wzajemnie przenikającą się sieć (rys. 1.1e). W materiałach ceramicznych, takie mikrostruktury są zwykle nieuporządkowane, a każda z przenikających się faz tworzy topologię szkieletu, składającego się z otwartych komórek połączonych ze sobą przestrzennymi mostkami. Taka struktura wyższego rzędu 2 występuje również w materiałach warstwowych (laminatach) [21] oraz gradientowych [22], posiadających ukierunkowany, zmienny gwałtownie lub jednostajnie, skład fazowy, wywołujący zauważalne zróżnicowanie budowy w skali setek mikrometrów.
Jedną z charakterystycznych cech mikrostruktury materiałów ceramicznych jest również obecność nieciągłości – porów oraz mikrospękań. Ich występowanie w tworzywie może wynikać z zamierzonych zabiegów technologicznych, prowadzących do otrzymania stałych pian lub materiałów komórkowych [23], albo przeciwnie – może być efektem niecałkowitego zagęszczenia materiału podczas syntezy, wskazującego na problemy albo ograniczenia technologiczne (rys. 1.1f).

Opis wewnętrznej budowy polikrystalicznych tworzyw ceramicznych wymaga również uwzględnienia struktury pojedynczych ziaren – a właściwie krystalitów, będących najmniejszymi elementami budującymi lity polikryształ. Ich anizotropia, wynikająca z ułożenia atomów w przestrzeni – periodycznego i specyficznego dla każdej z faz – istotnie wpływa na właściwości fizykochemiczne materiału. Decyduje ona o kinetyce spiekania, rozroście krystalitów w trakcie syntezy, ale również o końcowych właściwościach tworzywa, wynikających z przypadkowej orientacji przestrzennej poszczególnych krystalitów.
Oprócz struktur najgęstszego upakowania: regularnej płasko centrowanej (FCC, ang. Face-Centered Cubic), heksagonalnej zwartej (HCP, ang. Hexagonal Close-Packed) oraz bliskiej im, regularnej przestrzennie centrowanej (BCC, ang. Body-Centered Cubic), które są najbardziej rozpowszechnione wśród metali, fazy ceramiczne występują również w innych strukturach krystalicznych. Czynnik geometryczny, określany zasadą ,,najgęstszego ułożenia kul”, który pozwala tłumaczyć budowę wielu kryształów metalicznych, musi zostać uzupełniony o dodatkowe efekty wynikające ze specyfiki wiązań kowalencyjnych i jonowych [30–32]. W kryształach pierwiastków i związków chemicznych o dominującym charakterze kowalencyjnym, rozmieszczenie atomów w przestrzeni (w komórce elementarnej) wynika z kierunkowości wiązań (rozkładu gęstości elektronowej opisywanej orbitalami cząsteczkowymi), a w przypadku kryształów jonowych, na wzajemne ułożenie kationów i anionów (liczbę koordynacyjną), wpływa ładunek jonów oraz stosunek ich promieni. Klasyfikacja wybranych faz ceramicznych, ze względu na strukturę krystaliczną, została zawarta w tabeli [1.1].
W odróżnieniu od pokroju monokryształów, kształt krystalitów obecnych w litym materiale jest bardziej zróżnicowany. Wynika on z ograniczeń przestrzennych narzuconych przez sąsiadujące ze sobą ziarna, które oddzielone są od siebie granicami międzyziarnowymi. Granice te są kolejnym, ważnym elementem budowy polikryształów. W tworzywach ceramicznych decydują one o procesie syntezy (spiekania) i, bezpośrednio albo pośrednio, wpływają na wiele właściwości końcowych materiału takich jak: właściwości elektryczne, optyczne, ale również mechaniczne: kruchość, plastyczność czy podatność na pełzanie [33–35]. W klasycznym ujęciu, granice międzyziarnowe oddzielające zarówno różnie zorientowane krystality tej samej fazy jak i ziarna różnych faz, są traktowane jako dwuwymiarowe, płaskie defekty struktury krystalicznej, w których dochodzi do gwałtownej zmiany parametrów strukturalnych i fizykochemicznych [12, 35–37]. Jednak rozwój metod badawczych – doświadczalnych i symulacyjnych, który dokonał się w ostatnim dwudziestoleciu, pozwolił na dokładniejszą analizę wewnętrznej budowy granic międzyziarnowych. Aktualnie przyjmuje się, że obszar międzyziarnowy o grubości \(\sim\)0.2 nm–2 nm, można traktować jako odrębną międzyfazę. Ma ona specyficzne właściwości, swoją wewnętrzną strukturę i nie może występować samodzielnie, bez faz sąsiadujących [35, 38–41]. Wpływ granic międzyziarnowych na właściwości tworzyw staje się szczególnie widoczny, gdy rozmiary ziaren są niewielkie. W przypadku nanomateriałów, dla których rozmiar krystalitów dochodzi do 5 nm, gęstość granic międzyziarnowych jest bardzo duża (\(\sim\)1 × 1016 / mm3) i w związku z tym udział objętościowy fazy stanowiącej granice może przekraczać 50 % [42, 43].
W ujęciu makroskopowym, sprężystość materiałów polikrystalicznych jest efektem oddziaływań występujących w dwóch skalach. Na poziomie atomowym, odkształcenie komórki elementarnej, wywołane zewnętrznym obciążeniem, prowadzi do zmiany energii potencjalnej \(U_{\text{p}}\) sąsiadujących atomów, zależnej od ich rodzaju i ułożenia w sieci krystalicznej. Jeśli zatem przemieszczenie atomu \(u\), z pozycji równowagowej \(a_0\) (\(u = x - a_0\), przy czym \(x\), to nowa pozycja atomu), zostanie wywołane siłą \(F\), to wyrażając zmiany energii potencjalnej od przemieszczenia funkcją \(U_{\text{p}}(u)\) można zapisać, że: \[\label{eq:Upot_u} F = -\frac{\mathop{}\!\mathrm{d}U_{\text{p}}(u)}{\mathop{}\!\mathrm{d}u}.\] Ponieważ \(U_{\text{p}}\) zmienia się w sposób ciągły wraz ze zmianą \(u\), to możliwe jest przedstawienie jej w postaci szeregu Taylora: \[\label{eq:UpotTaylor} U_{\text{p}}(u) = U_{\text{p0}} + \left( \frac{\mathop{}\!\mathrm{d}U_{\text{p}}}{\mathop{}\!\mathrm{d}u } \right)_{\!a_0} \!\!\!\!u + \frac{1}{2} \left( \frac{\mathop{}\!\mathrm{d^2}U_{\text{p}}}{\mathop{}\!\mathrm{d}u^2 } \right)_{\!a_0} \!\!\!\!u^2 + \dots,\] w którym \(U_{\text{p0}}\) jest energią w położeniu równowagowym, a wszystkie kolejne pochodne ustalone są również względem \(a_0\). Dodatkowo, ponieważ minimum energii potencjalnej występuje dla \(a_0\), to \(\left(\mathop{}\!\mathrm{d}U_{\text{p}}/\mathop{}\!\mathrm{d}u \right)_{\!a_0} = 0\). Z uwagi na rozpatrywanie bardzo małych przemieszczeń (\(u \ll a_0\)), dalsze wyrazy szeregu można zaniedbać. Ostatecznie, zmiany energii potencjalnej dobrze przybliża więc wyrażenie: \[\label{eq:UpotTaylorApprox} U_{\text{p}}(u) = U_{\text{p0}} + \frac{1}{2} \left( \frac{\mathop{}\!\mathrm{d^2}U_{\text{p}}}{\mathop{}\!\mathrm{d}u^2 } \right)_{\!a_0} \!\!\!\!u^2.\] Podstawiając je zatem do równania \eqref{eq:Upot_u} otrzymuje się: \[\label{eq:Upot_uApprox} F = -\frac{\mathop{}\!\mathrm{d}U_{\text{p}}(u)}{\mathop{}\!\mathrm{d}u} = -\left( \frac{\mathop{}\!\mathrm{d^2}U_{\text{p}}}{\mathop{}\!\mathrm{d}u^2 } \right)_{\!a_0} \!\!\!\!u = -ku. \] Ponieważ \(\left( \mathop{}\!\mathrm{d^2}U_{\text{p}}/\mathop{}\!\mathrm{d}u^2 \right)_{\!a_0}\) jest drugą pochodną w minimum funkcji \(U_{\text{p}}(u)\), to jej wartość jest dodatnia i stała (\(k=\mathrm{const}\)). Wyrażenie powyższe, przedstawia więc prostą relację, która ilustruje rozciąganie sprężyny 3. Znając zatem zależność opisującą zmiany energii potencjalnej atomów w sieci krystalicznej od ich położenia (\(U_{\text{p}}(u)\)) można analizować podstawowe związki pomiędzy sprężystością a budową i właściwościami fizykochemicznymi w skali atomowej. Odpowiednie równania dla prostych układów (kryształów jonowych), można znaleźć w wielu opracowaniach z zakresu chemii, fizyki ciała stałego czy inżynierii materiałowej [12, 30, 31, 44]. Rozpatrując jednak rzeczywiste struktury krystaliczne, do ustalania parametrów opisujących właściwości sprężyste, stosuje się obecnie metody ab initio oraz dynamiki molekularnej (MD, ang. Molecular Dynamics) [45–48]. Wykorzystanie metod symulacyjnych, pozwala również na określanie właściwości sprężystych faz, dla których nie jest możliwe przeprowadzenie pomiarów bezpośrednich np. faz w granicach międzyziarnowych, albo faz metastabilnych.
Drugim czynnikiem, wpływającym istotnie na makroskopowe właściwości sprężyste polikryształów, jest przypadkowa orientacja krystalitów. Anizotropowe ziarna, które pod wpływem obciążeń odkształcają się niejednorodnie, oddziałując na siebie lokalnie, powodują, że globalna odpowiedź makroskopowego układu ziaren – ciała polikrystalicznego – jest zwykle izotropowa 4. Ustalenie efektywnych właściwości materiału (w szczególności jego sprężystości) na podstawie informacji o właściwościach faz składowych, stanowi główne zagadnienie mikromechaniki i jest rozwiązywane poprzez analityczną albo numeryczną homogenizację (zob. rozdz. 3.1).
W przedstawionym na wstępie rozumowaniu, mającym zilustrować związek pomiędzy fundamentalnymi oddziaływaniami na poziomie atomowym a makroskopową odpowiedzią ciała, założone zostało niewielkie odkształcenie wywołane zewnętrznym obciążeniem. Dzięki temu zachowanie rozpatrywanego kryształu mogło zostać opisane modelem liniowo-sprężystym. Taki modelowy materiał, nazywany materiałem Hooke’a, jest najczęściej stosowany do opisu właściwości sprężystych tworzyw ceramicznych. Pod wpływem obciążeń, ulegają one niewielkim odkształceniom, aż do wartości granicznych, przy których dochodzi do gwałtownej dekohezji. Analiza danych doświadczalnych potwierdza liniową zależność między naprężeniem a odkształceniem, która utrzymuje się w szerokim zakresie temperatury – dla ceramiki specjalnej, aż do wartości 0.7–0.8 temperatury topnienia, co w praktyce oznacza temperaturę powyżej 1000 °C.
Związki konstytutywne dla liniowych relacji pomiędzy tensorem naprężenia \(\mathbf{\sigma}\) i tensorem odkształcenia \(\mathbf{\varepsilon}\) ujmuje uogólnione prawo Hooke’a, które w zapisie wskaźnikowym przyjmuje postać 5 : \[\label{eq:Hooke} \sigma_{ij} = c_{ijkl} \varepsilon_{kl},\] w której wskaźniki \(i,j,k,l = 1,2,3\), a \(c_{ijkl}\) oznacza współczynniki sztywności, będące składowymi tensora sztywności \(\mathbf{C}\). Analogiczny związek można również zapisać dla relacji pomiędzy tensorem odkształcenia i naprężenia \(\varepsilon_{ij} = s_{ijkl} \sigma_{kl}\), w której \(s_{ijkl}\) oznacza współczynniki podatności sprężystej będące składowymi tensora podatności sprężystej \(\mathbf{S}\). Ponieważ tensory \(\mathbf{C}\) i \(\mathbf{S}\) są symetryczne (\(c_{ijkl}=c_{jikl}=c_{ijlk}=c_{klij}\) oraz \(s_{ijkl}=s_{jikl}=s_{ijlk}=s_{klij}\)) to liczba niezależnych współczynników redukuje się do 36 i można przedstawić je w zapisie macierzowym w notacji Voigta. Ponadto analiza warunków energetycznych w odkształcanym krysztale prowadzi do wniosku, że odpowiednie macierze są również symetryczne, co dalej redukuje liczbę niezależnych współczynników do 21 [49]. Ostatecznie dla najbardziej anizotropowego kryształu o najniższej symetrii – w układzie trójskośnym – macierz sztywności można zapisać jako 6 : \[C_{\alpha\beta} = \begin{bmatrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16} \\ & C_{22} & C_{23} & C_{24} & C_{25} & C_{26} \\ & & C_{33} & C_{34} & C_{35} & C_{36} \\ & & & C_{44} & C_{45} & C_{46} \\ &\text{sym}& & & C_{55} & C_{56} \\ & & & & & C_{66} \end{bmatrix}\] Wewnętrzna symetria kryształów należących do innych układów krystalograficznych dodatkowo redukuje liczbę niezależnych współczynników sztywności i podatności sprężystej. Dla układu jednoskośnego jest ich 13, dla rombowego 9, dla tetragonalnego i trygonalnego po 6, dla heksagonalnego 5, a dla regularnego jedynie 3. Postać odpowiednich macierzy sztywności, dla wymienionych układów krystalograficznych, można znaleźć w klasycznym opracowaniu Nye’a [49], albo wielu innych podręcznikach z zakresu mechaniki i inżynierii materiałowej.
W najprostszym przypadku, dla ciał izotropowych, do opisu właściwości sprężystych wystarczą dwa współczynniki sztywności i odpowiednią macierz można zapisać w postaci: \[C_{\alpha\beta} = \begin{bmatrix} C_{11} & C_{12} & C_{12} & 0 & 0 & 0 \\ & C_{11} & C_{12} & 0 & 0 & 0 \\ & & C_{11} & 0 & 0 & 0 \\ & & & \frac{1}{2}(C_{11}-C_{12}) & 0 & 0 \\ &\text{sym}& & & \frac{1}{2}(C_{11}-C_{12}) & 0 \\ & & & & & \frac{1}{2}(C_{11}-C_{12}) \end{bmatrix}\] Macierz ta, albo analogiczna macierz podatności sprężystej, może więc posłużyć do scharakteryzowania właściwości sprężystych izotropowych polikryształów. W praktyce inżynierskiej wykorzystywane są również stałe materiałowe: moduł Younga \(E\) (\(E=\sigma_{ii}/\varepsilon_{ii}\)), liczba Poissona \(\nu\) (\(\nu = -\varepsilon_{jj}/\varepsilon_{ii}\)) i moduł Kirchhoffa – inaczej moduł sprężystości poprzecznej \(\mathcal{G}\) (\(\mathcal{G}= \sigma_{ij} / \varepsilon_{ij}\); \(i \neq j\)). Związki pomiędzy inżynierskimi stałymi materiałowymi a odpowiednimi składowymi tensorów sztywności oraz podatności sprężystej, zarówno dla materiałów izotropowych jak i kryształów, można znaleźć w opracowaniach z zakresu fizyki ciała stałego, mechaniki i inżynierii materiałowej [12, 49–53].
Jak już wspomniano, tworzywa ceramiczne w szerokim zakresie temperatury wykazują zachowanie liniowo-sprężyste. Wzrost temperatury powoduje jednak obniżenie wartości współczynników sztywności i tym samym wartości modułów \(E\) i \(\mathcal{G}\). Obniżenie to jest jednak mniejsze niż w przypadku metali. Zmiany te dobrze ilustrują empiryczne zależności: zaproponowana dla modułu Younga przez Wachtmana [50] oraz ogólniejsza – dla współczynników sztywności – podana przez Varshniego [54]: \[\label{eq:YoungT} E=E_0 - bT \mathop{\mathrm{e}}^{\frac{-T_0}{T}},\] \[\label{eq:Varshni} C_{ij} = C_{ij}^0 - \frac{a}{\mathop{\mathrm{e}}^{\theta_e/T}-1}.\] W równaniach tych parametry \(E_0\) i \(C_{ij}^0\) odpowiadają odpowiednio wartościom modułu Younga i współczynnika sztywności, wyznaczonym dla temperatury 0 K. Pozostałe parametry równań uzyskiwane są poprzez dopasowanie powyższych zależności do wartości empirycznych ale można je powiązać z parametrami termodynamicznymi [54–56]. W równaniu \eqref{eq:YoungT} temperatura \(T_0\) może być więc przybliżana połową temperatury Debye’a, parametr \(b = 3R\gamma_{\text{G}}\delta_{\text{AG}}/V_0\), gdzie \(R\) to stała gazowa, \(\gamma_{\text{G}}\) parametr Grüneisena, \(\delta_{\text{AG}}\) parametr Andersona–Grüneisena [55], a \(V_0\) to średnia objętość atomowa. Z kolei w równaniu \eqref{eq:Varshni}, \(\theta_e\) jest efektywną temperaturą Einsteina oraz \(a\) jest parametrem dopasowania, który odpowiada za efekty anharmoniczne.
Analiza zmian właściwości sprężystych, wywołanych wpływem temperatury, przeprowadzona dla wielu monokryształów ceramicznych, potwierdza dobrą zgodność przedstawionych równań z danymi doświadczalnymi. Co ważniejsze, wskazuje również, że powyżej pewnej temperatury, a w szczególności powyżej temperatury pokojowej, występuje praktycznie liniowy spadek sztywności. Reguła ta sprawdza się także w przypadku ceramicznych materiałów polikrystalicznych, w których również obserwowane jest obniżenie wartości współczynników sztywności ze wzrostem temperatury. Jednak obecność granic międzyziarnowych powoduje, że w pewnej temperaturze, charakterystycznej dla międzyfazy, makroskopowe wartości modułów sprężystości gwałtownie maleją. Obniżenie to jest znacznie większe niż wynikałoby to z liniowej zależności, charakterystycznej dla materiału pozbawionego granic międzyziarnowych – monokryształu. Efekt ten przypisuje się lepkościowemu płynięciu materiału w granicach, który umożliwia przemieszczanie się ziaren względem siebie. Nie jest to już jednak efekt sprężysty i prowadzi do trwałej deformacji. Dla polikrystalicznych tworzyw ceramicznych, można zatem podać empiryczną regułę, dobrze sprawdzającą się w zakresie od temperatury pokojowej do temperatury, w której rozpoczyna się proces mięknięcia w granicach międzyziarnowych. W myśl tej reguły, wartości modułu Younga \(E\) i modułu sprężystości poprzecznej \(\mathcal{G}\) maleją o około 1 % przy wzroście temperatury o każde 100 K [50].
Po znormalizowaniu siły \(F/S=\sigma\) (gdzie \(S\) jest przekrojem poprzecznym, a \(\sigma\) naprężeniem prostopadłym do tego przekroju) i przemieszczenia \(u/L = \varepsilon\) (gdzie \(\varepsilon\) oznacza odkształcenie liniowe w kierunku zgodnym z przemieszczeniem), równanie \eqref{eq:Upot_uApprox} przedstawia prawo Hooke’a dla przypadku jednowymiarowego \(\sigma = E\varepsilon\), w którym \(E\) jest modułem Yonuga wyznaczonym na podstawie stałej \(k\) po normalizacji.↩︎
Izotropię właściwości fizycznych polikryształów ceramicznych, wynikającą z przypadkowej orientacji ziaren w polikrysztale, można uznać za cechę typową dla tego typu materiałów. Odróżnia to je od materiałów metalicznych, które w procesie produkcyjnym poddawane są obróbce plastycznej (walcowaniu, kuciu, wyciąganiu), powodującej kierunkową reorientację ziaren. Zjawisko izotropii polikryształów ceramicznych zostanie jeszcze dokładniej omówione w dalszej części np. zob. p. 1.3.3.↩︎
Jest to zapis przy pomocy niemych wskaźników w konwencji sumacyjnej Einsteina, który oznacza, że wyrażenie \eqref{eq:Hooke} jest równoważne sumowaniu po powtarzających się po prawej stronie równania wskaźnikach \(k\) i \(l\), zatem \(\sigma_{ij} = \sum\limits_{k=1}^{3}\sum\limits_{l=1}^{3} c_{ijkl}\varepsilon_{kl}\).↩︎
Dla odróżnienia od współczynników w zapisie tensorowym (\(c_{ijkl}\)), odpowiednie współczynniki w zapisie macierzowym zostaną zapisywane wielkimi literami (\(C_{\alpha\beta}\)), w którym wskaźniki \(\alpha,\beta = 1,2,\dots ,6\).↩︎
Jedną z najistotniejszych właściwości użytkowych materiałów konstrukcyjnych jest wytrzymałość mechaniczna. W szerokim znaczeniu pojęcie to określa zdolność do przenoszenia obciążeń. Opis fenomenologiczny wytrzymałości opiera się na analizie zależności między obciążeniem a odkształceniem, wyznaczonej w znormalizowanych warunkach. Dla wielu tworzyw ceramicznych do utraty spoistości dochodzi w zakresie odkształceń sprężystych – przy niewielkich deformacjach ciała, bez wcześniejszych oznak nadmiernego obciążenia. W praktyce takie zachowanie utrudnia zapobieganiu awariom i dlatego ten rodzaj niszczenia nazywa się katastrofalnym pękaniem [12]. Zjawisko to występuje w szerokim zakresie temperatury (zwykle pokrywającym zakres użytkowy), dlatego do opisu materiałów ceramicznych powszechnie stosowany jest model ciała sprężysto-kruchego. Ponieważ wytrzymałość zależy nie tylko od budowy materiału na poziomie atomowym, ale również jego mikrostruktury i warunków obciążania, to w rozważaniach warto rozdzielić te czynniki.
Wytrzymałość teoretyczna, nazywana również idealną czy kohezyjną, określona jest przez obciążenie, które prowadzi do niestabilności mechanicznej w sieci krystalicznej idealnego kryształu. Jest ona więc właściwością, która oferuje wgląd w związek pomiędzy wiązaniem chemicznym a symetrią kryształu. Jej znajomość jest użyteczna, ponieważ stanowi ona górną granicę wytrzymałości danego materiału, co może być ważną wskazówką przy projektowaniu i badaniu nowych tworzyw, ale również, odnosząc się do niej, można określić stopień zdefektowania badanej struktury. Dodatkowo, jest jedną z nielicznych właściwości mechanicznych, której wartość można wyznaczyć bezpośrednio metodami ab initio [47, 57–60].
W przypadku jednoosiowego rozciągania, wytrzymałość teoretyczną \(\sigma_{\text{t}}\) dla idealnego kryształu można oszacować na podstawie zależności podanej przez Polanyia [61] i Orowana [62, 63]: \[\label{eq:sigma_max} \sigma_{\text{t}}= \sqrt{\frac{E\gamma}{a_0}},\] w której \(E\) jest modułem Younga, \(\gamma\) energią powierzchniową odniesioną do jednostkowej powierzchni oraz \(a_0\) równowagową odległością międzyatomową w sieci krystalicznej. Wyniki obliczeń przeprowadzonych na podstawie powyższego równania pozwalają stwierdzić, że wytrzymałość teoretyczna materiału jest rzędu \(1/10\) wartości modułu Younga. Takie oszacowanie wskazuje, że wyznaczone doświadczalnie wartości wytrzymałości rzeczywistej litych tworzyw ceramicznych są zwykle o dwa albo trzy rzędy wielkości niższe od \(\sigma_{\text{t}}\) [12, 44]. Przyjmuje się, że za tak dużą różnicę odpowiedzialne są głównie wady obecne w materiałach, które pod wpływem obciążeń zapoczątkowują niekontrolowane pękanie. Zjawisko to zostało opisane przez Griffitha i będzie szerzej omówione w kolejnym punkcie (1.2.3).
Wytrzymałość rzeczywista, jak już wspomniano, zależy również od sposobu obciążenia. Najprostsza koncepcyjnie i najłatwiejsza w analitycznym opisie jest próba wytrzymałościowa, polegająca na jednoosiowym rozciąganiu. W przypadku ceramiki, jej prawidłowe przeprowadzenie nastręcza jednak wiele trudności. Przygotowanie odpowiednio licznej serii normatywnych próbek jest kosztowne, czasochłonne, a sama preparatyka stanowi poważne wyzwanie [64, 65]. Dodatkowo, nawet niewielkie niewspółosiowości obciążenia lub nieregularności kształtu próbki, wywołują momenty gnące, które zakłócają jednorodny, teoretyczny stan naprężenia i, przy braku możliwości plastycznego odkształcenia, prowadzą do jej wcześniejszego zerwania [66–68].
W próbie jednoosiowego ściskania materiały ceramiczne wykazują największą wytrzymałość. Jest ona tak duża, że jej wyznaczanie sprawia poważne problemy aparaturowe. Techniki stosowane dla materiałów ceramicznych o niższej wytrzymałości (ceramiki tradycyjnej, tynków, zapraw murarskich, betonów czy skał) nie sprawdzają się przy badaniu tworzyw z grupy ceramiki specjalnej [69]. Główny problem badawczy, poza aparaturą posiadającą wystarczający zakres pomiarowy, wyposażoną w wysokowytrzymały osprzęt (talerzyki pomiarowe), dotyczy przeciwdziałaniu miejscowym spiętrzeniom naprężeń, wynikającym z nierównomiernego przylegania czołowych powierzchni próbek do uchwytów przenoszących obciążenie [15, 70]. Próbki do tego typu badania, muszą zatem wykazywać wąski zakres tolerancji dla gładkości i równoległości powierzchni czołowych.
Wymienione trudności, w efektywnym przeprowadzaniu pomiarów wytrzymałości podczas jednoosiowego rozciągania i ściskania zaawansowanej ceramiki konstrukcyjnej, spowodowały, że powszechnie stosowaną metodą pomiarową, stała się próba jednoosiowego zginania [15, 53]. W badaniu zakłada się, że odkształcenia wywołane jednoosiowym obciążeniem, rozkładają się liniowo: od maksymalnego rozciągania – przy jednej z powierzchni, do maksymalnego ściskania – przy powierzchni przeciwległej. Aby spełnione zostały takie założenia, w praktyce stosuje się metodę trój- albo czteropunktowego zginania normatywnych belek. W próbach tych wymagania aparaturowe są znacznie niższe, a konfiguracja osprzętu niezbędnego do przeprowadzenia pomiaru, pozwala na łatwe zaadaptowanie ich również do warunków wysokotemperaturowych [64, 71]. Źródła możliwych błędów pomiarowych wynikają tutaj ze sposobu przyłożenia obciążeń, które mogą powodować miejscowe kruszenie próbki, niszczenie poprzez ścinanie albo skręcanie. Problemy te są jednak łatwe do zidentyfikowania na podstawie obserwacji próbek po badaniu i tym samym do ich wyeliminowania [64, 66]. Największą trudność sprawia przygotowanie powierzchni próbki, która jest narażona na rozciąganie i powinna być wolna od wad obróbki, mogących istotnie zaniżyć wyniki pomiarów [71].
Wyznaczanie wytrzymałości rzeczywistej tworzyw ceramicznych, wymaga wykonania pomiarów dla dużej populacji próbek (\(>30\)). W tym kontekście, metody pozwalające na przeprowadzenie pomiarów dających statystycznie istotne wyniki przy zakładanym poziomie ufności, na próbkach, których preparatyka jest stosunkowo szybka i tania, nabierają szczególnego znaczenia. Taką metodą może być próba dwuosiowego zginania, w której tolerancja dotycząca kształtu oraz wykończenia powierzchni próbki jest znacznie większa. Również objętość materiału niezbędna do przygotowania normatywnej kształtki jest niewielka, co może mieć istotne znaczenie w badaniach naukowych i pracach badawczo-rozwojowych prowadzonych w skali laboratoryjnej.
Próbę dwuosiowego zginania można przeprowadzać w kilku wariantach, różniących się rodzajem i rozmieszczeniem podpór oraz sposobem przekazywania obciążenia [72–77]. Najczęściej stosowane są warianty polegające na centralnym obciążaniu cienkiej cylindrycznej płytki, podpartej na trzech kulkach, rozmieszczonych przy zewnętrznej krawędzi próbki pod kątem 120 ° (BOTB, ang. ball-on-three-ball i POTB, ang. piston-on-three-ball) [15]. Wyznaczanie wytrzymałości w złożonym stanie naprężeń, odpowiada warunkom w jakich często użytkowane są elementy wykonane z tworzyw ceramicznych. Dlatego wyniki tych badań stanowić mogą również wartościowe uzupełnienie i rozszerzenie danych, uzyskiwanych metodami opartymi na obciążeniu jednoosiowym [64, 78–82].
Wyniki pomiarów wytrzymałości rzeczywistej dla materiałów ceramicznych, niezależnie od zastosowanej metody badawczej, charakteryzują się dużym rozrzutem – nierzadko na poziomie 10 %, a różnice pomiędzy wartościami ekstremalnymi dla próbek należących do tej samej partii mogą przekraczać 50 % [12, 71]. Jakościowo można to tłumaczyć obecnością defektów, których rozmieszczenie i orientacja w materiale jest przypadkowa. Takie zachowanie ma jednak istotne konsekwencje inżynierskie. Po pierwsze, aby zapewnić wymagany margines bezpieczeństwa, wytrzymałość, którą zakłada się projektując element konstrukcji, musi być znacznie niższa niż wartość średnia dla stosowanego tworzywa. Po drugie, prawdopodobieństwo zniszczenia, przy określonym obciążeniu, rośnie wraz z rozmiarem elementu. Dlatego ważny staje się ilościowy opis tego zjawiska. Zmienność wytrzymałości można opisywać różnymi rozkładami statystycznymi [83–87], jednak dla tworzyw ceramicznych powszechnie stosowany jest rozkład zaproponowany przez Weibulla [88, 89]. Rozkład ten został opracowany na podstawie analizy danych eksperymentalnych i opiera się na zasadzie najsłabszego ogniwa, w myśl której za wytrzymałość badanej próbki odpowiedzialny jest element najmniej trwały – w którym znajdzie się defekt krytyczny. Statystyczna teoria wytrzymałości, rozwinięta na podstawie prac Weibulla, pozwoliła na wprowadzenie skutecznej metodyki, opierającej się na badaniach próbnych (ang. proof testing)[90, 91], która wykorzystywana jest z powodzeniem przy kontroli jakości i niezawodności komponentów wykonanych z tworzyw ceramicznych [50, 92, 93].
Nagłe zniszczenie materiału – jego dekohezja, wynikająca z braku możliwości relaksacji naprężenia poprzez odkształcenie plastyczne, jest głównym czynnikiem ograniczającym szerokie wykorzystanie tworzyw ceramicznych w roli materiałów konstrukcyjnych. Zjawisko kruchego pękania, stanowi więc od wielu lat główne zagadnienie, wokół którego koncentruje się uwaga inżynierów materiałowych, zajmujących się tą grupą tworzyw.
Pierwsze, energetyczne kryterium kruchego pękania, zostało sformułowane przez Griffitha [94, 95] i opierało się na założeniu, że zmiana energii mechanicznej ciała zawierającego szczelinę, wywołana pracą \(W\), wykonaną przez zewnętrzne obciążenia, zostaje w nim skumulowana w postaci energii odkształceń sprężystych \(U_{\text{e}}\) oraz dodatkowo energii powierzchniowej \(U_{\text{s}}\), co można zapisać równaniem: \[\label{eq:Griffith_balans} W = U_{\text{e}}+ U_{\text{s}}.\]
Wprowadzenie do bilansu energetycznego energii powierzchniowej, pozwoliło Griffithowi pogodzić wyniki analizy przeprowadzonej nieco wcześniej przez Inglisa [96] ze znanymi faktami doświadczalnymi dotyczącymi pękania materiałów kruchych. Z analizy Inglisa wynikało bowiem, że wprowadzenie eliptycznej szczeliny, o długości osi wielkiej \(2c\), do jednorodnie obciążonego ośrodka, obniża energię układu – relaksuje go, a tym samym proces pękania, niezależnie od wymiarów szczeliny, powinien być samorzutny. Takie wnioski były w opozycji do wyników doświadczeń, z których wynikało, że rozmiar wad obecnych w materiale ma istotny wpływ na wartość naprężenia, przy którym dochodzi do inicjacji pękania. Uwzględnienie dodatkowego czynnika hamującego ten proces, pozwoliło więc na ustalenie wartości granicznej naprężenia, przy którym szczelina może stać się źródłem niekontrolowanego pękania.
Griffith oparł się na warunku równowagi niestabilnej, który musi zostać zachowany w ciele przy stałym przemieszczeniu (\(\mathop{}\!\mathrm{d}W = 0\)): \[\label{eq:Griffith_diff_balans} - \frac{\mathop{}\!\mathrm{d}{}U_{\text{e}}}{\mathop{}\!\mathrm{d}{}c} = \frac{\mathop{}\!\mathrm{d}{}U_{\text{s}}}{\mathop{}\!\mathrm{d}{}c}\] Warunek ten oznacza, że jeśli nieskończenie mały przyrost długości szczeliny (\(\mathop{}\!\mathrm{d}c\)) spowoduje w ciele obniżenie energii odkształceń sprężystych o wartość równą, a tym bardziej większą od wartości energii potrzebnej na wytworzenie nowej powierzchni, to zainicjuje on dalsze samorzutne powiększenie się szczeliny.
Aby określić zmianę energii odkształceń sprężystych wywołaną przyrostem długości szczeliny o \(\mathop{}\!\mathrm{d}{}c\), Griffith wykorzystał równanie podane przez Inglisa dla nieograniczonej płyty o jednostkowej grubości (\(w = 1\)) i module Younga \(E\), w której znajduje się eliptyczna szczelina: \[\label{eq:Inglis} U_{\text{e}}= \frac{\pi \sigma^2 c^2}{E}.\] Wartość energii powierzchniowej dla takiej szczeliny o powierzchni \(2\!\cdot\!(2cw)\) wyraził jako: \[\label{eq:Griffith_gamma} U_{\text{s}}= 2 (2cw) \gamma = 4c\gamma, \quad \text{gdy } w=1,\] przy czym \(\gamma\) to energia powierzchniowa przypadająca na jednostkę powierzchni.
Podstawienie powyższych równań \eqref{eq:Inglis} i \eqref{eq:Griffith_gamma} do warunku równowagi \eqref{eq:Griffith_diff_balans}, umożliwiło ostatecznie na obliczenie zmian energii wywołanych przez nieskończenie mały przyrost długości szczeliny i analityczne określenie warunku równowagi: \[\label{eq:Griffith_balans_analitical} \frac{\pi \sigma^2 c}{E} = 2\gamma\] oraz ustalenie krytycznej wartości obciążenia \(\sigma_{\text{c}}\), przy którym szczelina o długości \(2c\) zaczyna się powiększać – co zapoczątkowuje katastrofalne pękanie: \[\label{eq:Griffith_PSN} \sigma_{\text{c}}= \sqrt{\frac{2E\gamma}{\pi c}}.\]
Związek powyższy nazwany równaniem Griffitha 7 , stanowił ważny etap w rozwoju prac nad opisem mechanizmu kruchego pękania. Występujący w nim iloczyn \(2\gamma\), pozwalał bowiem na ilościowe określenie oporu \(R\), jaki stawiany jest przez materiał podczas rozprzestrzeniania się pęknięcia.
Wyniki przeprowadzonych pomiarów wskazywały jednak, że rzeczywista wartość takiego oporu jest znacznie większa niż wartość oszacowana na podstawie termodynamicznej energii powierzchniowej \(\gamma\). Wynikało to przede wszystkim z uwzględnienia w zaproponowanym przez Griffitha warunku równowagi \eqref{eq:Griffith_diff_balans}, wyłącznie efektu związanego z energią powierzchniową, a pominięciem pozostałych sposobów dyssypacji energii takich jak: lokalne odkształcenie plastyczne, emisja akustyczna, wymiana energii na drodze promieniowania cieplnego i innych składników mogących zwiększać rzeczywistą odporność materiału na pękanie. Dlatego Orowan i Irwin [63, 97] zaproponowali, aby wartość \(\gamma\) zastąpić efektywną energią powierzchniową \(\gamma^{*}\), która łączyłaby wszystkie istotne czynniki i dzięki temu mogłaby być miarą odporności na kruche pękanie.
Jednak z powodów praktycznych [51], wynikających z trudności w wyznaczaniu \(\gamma^{*}\), a tym samym stosowaniu kryterium energetycznego, upowszechnił się inny, makroskopowy parametr, wprowadzony przez Irwina [99]. W swoim rozumowaniu oparł się on na kryterium siłowym i wykorzystał w nim współczynnik intensywności naprężeń \(K\). Pole naprężeń w pobliżu szczeliny, dla przypadku dwuwymiarowego, opisał on przy pomocy funkcji naprężeń zaproponowanej przez Westergaarda [98]: \[\label{eq:Irwin_pole} \sigma_{ij} = \frac{K_m}{\sqrt{2\pi r}} f_{ij,m}(\theta),\] w której \(\sigma_{ij}\) reprezentuje składowe tensora naprężenia dla punktu o współrzędnych biegunowych \(r\) i \(\theta\), w układzie współrzędnych o początku umieszczonym w wierzchołku szczeliny (rys. 1.2), \(f_{ij,m}(\theta)\) jest bezwymiarowym współczynnikiem określającym zmienność kątową naprężenia [92], natomiast indeks \(m\) określa typ obciążenia szczeliny: I, II i III (rys. 1.3).
Irwin zauważył, że równanie powyższe \eqref{eq:Irwin_pole} pozwala na określenie stanu naprężenia w pobliżu szczeliny, niezależnie od geometrii próbki, konfiguracji szczeliny oraz sposobu jej obciążenia, a parametrem, który uwzględnia wszystkie te elementy jest współczynnik intensywności naprężeń \(K_m\).
Dla pierwszego typu obciążenia (\(m = \text{I}\)), działające na szczelinę naprężenia są prostopadłe do powierzchni pękania. Przy dostatecznie dużej grubości próbki (w PSO) ograniczona zostaje możliwość dyssypacji energii poprzez odkształcenie plastyczne – strefy plastyczne są wtedy znikomo małe w porównaniu do wymiarów ciała oraz szczeliny – tym samym niszczenie zachodzi praktycznie, wyłącznie w sposób kruchy. Można zatem przyjąć, że w takim przypadku, dla próbki o przyjętej geometrii i konfiguracji szczeliny, będzie istnieć graniczna wartość współczynnika intensywności naprężeń, przy której, w rozpatrywanym układzie ciała ze szczeliną, panować będzie równowaga, natomiast przy większych wartościach \(K_\text{I}\), dochodzić będzie do szybkiego rozprzestrzeniania się pęknięcia. Warunek ten, można zapisać równaniem: \[\label{eq:Irwin_equilibrium} K_\text{I} = K_{\text{Ic}},\] w którym \(K_{\text{Ic}}\) jest krytycznym współczynnikiem intensywności naprężeń dla pierwszego typu obciążenia szczeliny. W liniowej mechanice pękania, równanie to stanowi podstawowe, siłowe kryterium pękania, w myśl którego współczynnik intensywności naprężeń \(K_\text{I}\), charakteryzujący pole naprężeń w pobliżu wierzchołka szczeliny, nie może przekroczyć wartości krytycznej, która jest określona wartością \(K_{\text{Ic}}\) [50, 51].
Obliczenie wartości współczynnika \(K_\text{I}\) na podstawie równania \eqref{eq:Irwin_pole} jest jednak trudne i analityczne rozwiązania istnieją jedynie dla prostych kształtów o wybranej konfiguracji szczeliny i obciążenia. Rozwiązania dla bardziej skomplikowanych przypadków uzyskuje się zwykle metodami numerycznymi [100–104]. Z kolei współczynnik \(K_{\text{Ic}}\) jest stałą materiałową i jego wartości wyznaczane są doświadczalnie, z uwzględnieniem znormalizowanych kształtów próbek i obciążeń [105–107]. Równanie pozwalające na określenie wartości \(K_{\text{Ic}}\) na podstawie wyników pomiarów wytrzymałościowych można zapisać ogólnym wyrażeniem [108, 109]: \[\label{eq:KIc} K_{\text{Ic}}= Y\sigma_{\text{c}}\sqrt{c},\] w którym \(Y\) jest bezwymiarowym parametrem, zależnym od geometrii próbki (uwzględniającym jej skończone wymiary) oraz sposobu przyłożenia obciążenia.
Dla materiałów ceramicznych, w których do zniszczenia dochodzi głównie za sprawą pierwszego typu obciążeń, współczynnik \(K_{\text{Ic}}\) uznawany jest więc za miarę odporności na kruche pękanie. Typowe wartości \(K_{\text{Ic}}\) dla szkieł i monokryształów ceramicznych zawierają się w zakresie 0.5 MPa m1/2–2 MPa m1/2 [110]. Dla polikrystalicznych tworzyw ceramicznych są większe i zwykle mieszczą się w przedziale 2 MPa m1/2–10 MPa m1/2 [93]. Są to jednak wartości niewielkie w porównaniu do materiałów metalicznych, dla których wartości \(K_{\text{Ic}}\) zwykle przekraczają 10 MPa m1/2, a dla niektórych stopów osiągają wartości ponad 200 MPa m1/2 [52, 111–114].
Kryterium Irwina \eqref{eq:Irwin_equilibrium} można również wyrazić w ujęciu energetycznym. Wtedy ilość energii \(G\), przypadającej na jednostkę nowej powierzchni \(A\), która została dostarczona na sposób pracy \(W\) wykonanej przez obciążenie zewnętrzne 8 i pomniejszona o skumulowaną w ciele energię wewnętrzną w postaci odkształceń sprężystych, można zapisać równaniem: \[\label{eq:Irwin_energy_balans} G = \frac{\mathop{}\!\mathrm{d}W}{\mathop{}\!\mathrm{d}A} - \frac{\mathop{}\!\mathrm{d}U_{\text{e}}}{\mathop{}\!\mathrm{d}A}.\] Równanie to, określa więc szybkość uwalniania energii w odniesieniu do powierzchni (nie czasu) i jest równoważne energetycznemu warunkowi Griffitha \eqref{eq:Griffith_balans}, wyrażonemu w formie różniczkowej względem \(\mathop{}\!\mathrm{d}A\) (\(\mathop{}\!\mathrm{d}A = w \mathop{}\!\mathrm{d}c\)). Można zatem napisać, że: \[\label{eg:G_diff} G = \frac{\mathop{}\!\mathrm{d}U_{\text{s}}}{\mathop{}\!\mathrm{d}A},\] więc \[\label{eq:G_2gamma} G \geqslant G_{\text{c}}= 2\gamma^{*}= R.\] Oznacza to, że gdy szybkość uwalniania energii sprężystej \(G\), przekroczy pewną wartość krytyczną \(G_{\text{c}}\), równą oporowi stawianemu przez materiał \(R\), to dojdzie do wzrostu długości szczeliny. \(G_{\text{c}}\) wyraża więc energię, która odpowiada pracy, jaka musi zostać wykonać na ciele, w celu utworzenia nowej powierzchni szczeliny w trakcie pękania. Dlatego \(G_{\text{c}}\) nazywana jest energią pękania albo pracą pękania. Dodatkowo, rozważając pierwszy typ obciążenia dla nieograniczonej płaskiej płyty ze szczeliną, na podstawie równania \eqref{eq:Griffith_PSN} i \eqref{eq:G_2gamma} oraz przyjmując, że w równaniu \eqref{eq:KIc} \(Y = \sqrt{\pi}\) (szczelina Griffitha), można podać związek pomiędzy \(G_{\text{Ic}}\) i \(K_{\text{Ic}}\) w PSN 9: \[\label{eq:GIc_KIc} G_{\text{Ic}}= \frac{K_{\text{Ic}}^2}{E}.\] Równanie to pozwala więc na empiryczne wyznaczanie energii pękania \(G_{\text{Ic}}\) i tym samym efektywnej energii powierzchniowej \(\gamma^{*}\).
Opisane kryteria – zarówno Griffitha, jak również Irwina – wskazują, że gdy obciążenie osiągnie pewną graniczną wartość \(\sigma_{\text{c}}\), przy którym przekroczony zostanie stały opór materiału \(R\), to będąca źródłem pękania obecna w nim krytyczna wada, zacznie się szybko powiększać. Szybkość uwalniania energii sprężystej osiągnie wtedy wartość krytyczną \(G_{\text{c}}\), co spowoduje niekontrolowane pękanie. Zachowanie takie jest charakterystyczne jedynie dla materiałów idealnie kruchych i obserwuje się je zwykle w szkłach i niektórych monokryształach ceramicznych [92, 115]. W polikrystalicznych tworzywach ceramicznych wartości \(R\) i \(G_{\text{c}}\) nie są stałe i mogą wzrastać wraz z wydłużaniem pęknięcia [116–120]. Osiągnięcie wartości \(G_{\text{c}}\) powoduje w takich materiałach wydłużenie szczeliny o \(\mathop{}\!\mathrm{d}c\) i wzrost wartości oporu \(R\). Jeśli aktualna wartość \(G\) nie przekracza nowo ustalonej wartości \(G_{\text{c}}\) to prowadzi to do dalszego stabilnego wzrostu długości szczeliny albo do całkowitego zahamowania procesu. Zmodyfikowany warunek pękania w takim przypadku można więc zapisać jako: \[\label{eq:R_balans} \frac{\mathop{}\!\mathrm{d}G}{\mathop{}\!\mathrm{d}c} \geqslant \frac{\mathop{}\!\mathrm{d}R}{\mathop{}\!\mathrm{d}c}.\]
Zależność oporu materiału od długości szczeliny nazywana jest krzywą oporu albo z krzywą ,,R” 10. Analiza zmienności tej krzywej pozwala na uzyskanie dodatkowych informacji o zjawisku pękania. Zachowanie materiału zgodne z krzywą ,,R” wskazuje, że w trakcie dekohezji uruchamiane są mechanizmy zwiększające energię pękania. Niektóre z nich wynikają bezpośrednio z właściwości faz budujących materiał (np. anizotropia właściwości sprężystych i cieplnych skutkująca pojawieniem się resztkowych naprężeń cieplnych czy przemiana martenzytyczna wywołująca lokalny wzrost naprężenia wywołany zmianą objętości), a inne mają swoje źródło w mikrostrukturze (np. blokowanie rozwoju szczeliny na skutek tarcia między jej powierzchniami czy mostkowanie). Mechanizmy te zostaną szerzej omówione w kolejnych rozdziałach (1.3.3 i 1.3.5).
Liniowa mechanika pękania, opierająca się na przytoczonych tutaj równaniach, pozwala na fenomenologiczny opis warunków krytycznych, w których pęknięcie staje się mechanicznie niestabilne i zaczyna się rozprzestrzeniać. Jednak inicjacja pękania, zawsze rozpoczyna się od ,,dyskretnego zdarzenia” w skali atomowej, polegającego na zerwaniu wiązań chemicznych między sąsiadującymi atomami [121]. Klasyczne teorie, opierając się na nielokalnych kryteriach pękania, nie pozwalają na ujęcie takiego efektu. Przy próbie lokalizacji, w równaniach opisujących pole naprężenia w pobliżu szczeliny, pojawia się osobliwość (\(\sigma \sim 1/\sqrt{r} \rightarrow \infty\), gdy \(r \rightarrow 0\)) [99, 122]. Problem ten staje się szczególnie istotny w przypadku nanomateriałów, w których rozmiary krystalitów i związane z nini rozmiary defektów krytycznych, zaczynają wykraczać poza granice stosowalności liniowej mechaniki pękania. Dlatego od wielu lat podejmowane są próby analitycznego rozwiązania tego zagadnienia, uwzględniające dyskretną i zarazem stochastyczną naturę zjawiska pękania [123]. Wykorzystywane są w nich dyskretne kryteria rozpraszania energii [122, 124, 125], czy skwantowane rozmiary defektów będące wielokrotnością stałej sieciowej w komórce elementarnej [126]. Podejście takie, ma na celu sformułowanie kwantowej mechaniki pękania (QFM, ang. Quantized Fracture Mechanics), która obejmowałaby zarówno obszar należący do liniowej jak i nieliniowej mechaniki pękania [126–128]. W ostatnich latach, do analizy zjawiska pękania, coraz częściej wykorzystywane są jednak metody przybliżone, opierające się na dynamice molekularnej [47, 57, 59, 121, 129], które omówione będą w dalszej części (np. zob. p. 1.3.5).
Przedstawione rozumowanie zostało sformułowane dla płaskiej, nieograniczonej w dwóch wymiarach, płyty o jednostkowej grubości \(w\), co odpowiada warunkom płaskiego stanu naprężenia (PSN). Równanie Griffitha można również zapisać dla płaskiego stanu odkształcenia (PSO), wtedy odpowiednie równanie, będzie różniło się od równania \eqref{eq:Griffith_PSN} o czynnik \(1/(1-\nu^2)\), w którym \(\nu\) jest liczbą Poissona.↩︎
Przyjęta tutaj konwencja zakłada, że praca wykonana przez otoczenie na układzie ma znak dodatni (\(W > 0\)).↩︎
Dla PSO równanie \eqref{eq:GIc_KIc} będzie różniło się o czynnik \(1-\nu^2\).↩︎
Analogiczną krzywą można również przedstawić dla zmienności \(K_{\text{Ic}}\) względem długości szczeliny. Krzywa taka nazywana jest krzywą kruchości albo krzywą ,,T” (ang. toughness).↩︎
Zjawisko rozszerzalności cieplnej materiałów polikrystalicznych – podobnie jak omawiana wcześniej sprężystość – może być rozpatrywane w dwóch skalach. W skali atomowej, rozszerzalność cieplna jest przejawem anharmoniczności drgań atomów w sieci krystalicznej. Teoretyczne podstawy opisu tego zjawiska zostały sformułowane przez Grüneisena [130, 131]. Opierając się na harmonicznym przybliżeniu dla drgań atomów, wprowadził on bezwymiarowy parametr 11 \(\gamma_{\text{G}}\), wyrażający zmianę częstości tych drgań \(\nu\) wywołaną zmianą objętości ciała (\(\gamma_{\text{G}}= - (\mathop{}\!\mathrm{d}\log \nu)/(\mathop{}\!\mathrm{d}\log V)\)). Takie quasi-harmoniczne przybliżenie, pozwoliło na sformułowanie związku między objętościową rozszerzalnością cieplną \(\beta\) a parametrami termodynamicznymi – ciepłem właściwym \(C_V\) i ściśliwością izotermiczną \(\chi_T\) (\(\chi_T = - 1/V(\partial V/\partial P)_{T}\)), który można przedstawić równaniem: \[\label{eq:GruneisenBeta} \beta = \gamma_{\text{G}}\frac{C_V \chi_T}{V}.\]
Aby uwzględnić wpływ symetrii kryształu, która może sprawiać, że zmiany objętości wywołują niejednakowe zmiany dla różnych rodzajów drgań (modów), iloczyn \(\gamma_{\text{G}} C_V\), w równaniu zaproponowanym przez Grüneisena, zastępuje się sumą iloczynów odpowiednich składowych wyznaczonych dla kolejnych rodzajów drgań (\(\sum {\gamma_{\text{G}}}_i C_i\)) [132, 133]. Potwierdzona użyteczność parametru Grüneisena w odniesieniu do opisu zjawiska rozszerzalności cieplnej, ale również do analizy zmian właściwości sprężystych pod wpływem temperatury, powoduje, że jest on często wykorzystywany i wyznaczany metodami analitycznymi jak i przybliżonymi [134–137].
Rozpatrując zjawisko rozszerzalności cieplnej w skali makroskopowej należy uwzględnić również efekty wynikające z przypadkowej orientacji ziaren w polikryształach. Po pierwsze, podobnie jak w przypadku właściwości sprężystych, w dużej objętość materiału w porównaniu do objętości pojedynczego ziarna, następuje uśrednianie lokalnej anizotropii krystalitów. W związku z tym, makroskopowa odpowiedź polikryształów ceramicznych na zmianę temperatury jest izotropowa. Po drugie, lokalne zróżnicowanie rozszerzalności cieplnej wywołuje niejednorodne odkształcenia ziaren. Prowadzi to do powstawania naprężeń cieplnych pomiędzy sąsiadującymi ze sobą krystalitami. Dla tworzyw ceramicznych zjawisko to jest szczególnie istotne, ponieważ metody syntezy opierają się na procesach fizykochemicznych przebiegających w temperaturze znacznie przewyższającej późniejszą temperaturę użytkowania. Ochładzanie materiału po syntezie prowadzi więc do powstawania w nim resztkowych naprężeń cieplnych. Wartości naprężeń skumulowanych w litym materiale podczas syntezy zależą istotnie od właściwości faz składowych ale również od mikrostruktury tworzywa. Zjawisko to zostanie szerzej omówione w rozdziale 1.4, tutaj warto zauważyć jedynie, że naprężenia te mogą niekiedy osiągać wartości rzędu GPa, przez co istotnie wpływają na końcowe właściwości tworzywa.
Do opisu zmian wymiarów ciała wywołanych zmianami temperatury, oprócz współczynnika objętościowego \(\beta\), stosuje liniowy współczynnik rozszerzalności cieplnej \(\alpha\). W sensie fizycznym określa on wydłużenie względne (\(\Delta l/l_0\)), wywołane nieskończenie małym przyrostem temperatury przy stałym ciśnieniu: \[\label{eq:alfaFiz} \alpha(T) = \lim_{\Delta T \to 0} \frac{1}{l_0}\frac{\Delta l}{\Delta T} = \frac{1}{l_0}\left( \frac{\mathop{}\!\mathrm{d}l}{\mathop{}\!\mathrm{d}T} \right)_{\!p}\] i dla ciał izotropowych można przyjąć, że \(\beta \approx 3 \alpha\).
Na podstawie tak zdefiniowanego współczynnika rozszerzalności cieplnej, można więc określić odkształcenie cieplne \(\varepsilon^{\text{T}}\), wywołane zmianą temperatury w zakresie od temperatury referencyjnej \(T_0\) do \(T_1\): \[\label{eq:thermal_strain_def} \varepsilon^{\text{T}}= \int\limits_{T_0}^{T_1}\alpha(T)\mathop{}\!\mathrm{d}T.\]
Ponieważ liniowy współczynnik rozszerzalności cieplnej wykazuje niewielkie zmiany w szerokich zakresach temperatury, to często – szczególnie w praktyce inżynierskiej – wykorzystywany jest średni, techniczny współczynnik rozszerzalności cieplnej \(\overline{\alpha}\), opisujący wydłużenie względne w określonym przedziale temperatury: \[\label{eq:alfaTech} \overline{\alpha}(T_0,T_1) = \frac{1}{l_0}\frac{l - l_0}{T_1-T_0},\] Wyznaczone w ten sposób wartości średniego współczynnika rozszerzalności cieplnej, pozwalają więc na szybkie obliczenie wydłużenia (bądź skrócenia) próbki czy elementu, w interesującym zakresie temperatury (\(\Delta l = l_0 \overline{\alpha} \Delta T\)). Dokładność takiego oszacowania jest tym większa, im rozpatrywany zakres temperatury jest bliższy zakresowi, w którym został doświadczalnie wyznaczony współczynniki \(\overline{\alpha}\).
Aby jednak w pełni scharakteryzować deformacje ciała, a w szczególności kryształu, wynikające ze zmian temperatury, czyli zdefiniować odkształcenie cieplne, należy posłużyć się zapisem tensorowym: \[\label{eq:thermStrain} \varepsilon^{\text{T}}_{ij} = \alpha_{ij}\Delta T,\] z którego wynika, że przy dostatecznie małej zmianie temperatury \(\Delta T\) wywołującej jednorodną deformację rozpatrywanego ciała, wszystkie składowe tensora odkształcenia \(\varepsilon^{\text{T}}_{ij}\) są proporcjonalne do zmiany temperatury. W takim ujęciu tensor rozszerzalności cieplnej \(\mathbf{\alpha}\) określony jest dziewięcioma składowymi \(\alpha_{ij}\) (tensor drugiego rzędu, tak jak tensor odkształcenia \(\mathbf{\varepsilon}\)). Ponieważ tensor \(\mathbf{\alpha}\) jest tensorem symetrycznym (\(\alpha_{ij} = \alpha_{ji}\)), to liczba niezależnych składowych redukuje się do sześciu. Podczas opisu odkształcenia cieplnego kryształów, taka liczba niezależnych składowych \(\alpha_{ij}\) wymagana jest jedynie dla kryształów z układu trójskośnego. Wzrost symetrii powoduje obniżenie liczby składowych i dla układu jednoskośnego wymagane są cztery składowe, dla rombowego – trzy, dla tetragonalnego, trygonalnego i heksagonalnego – dwie, a w układzie regularnym wystarczy jedna składowa 12, co oznacza, że w układzie tym rozszerzalność cieplna jest izotropowa 13. Podobne właściwości wykazują polikryształy ceramiczne, w których niezależnie od symetrii krystalitów, dochodzi do uśredniania lokalnej anizotropii krystalitów i do opisu makroskopowej rozszerzalności cieplnej potrzebna jest znajomość jednej składowej tensora \(\mathbf{\alpha}\). Wartość tej składowej, czyli liniowego współczynnika rozszerzalności cieplnej, dla litych tworzyw ceramicznych jest zatem stała (w danej temperaturze i ciśnieniu) i niezależna od konfiguracji próbki. Odstępstwa od tej reguły mogą świadczyć o pojawieniu się tekstury, ale częściej są one związane z obecnością w tworzywie wydłużonych albo spłaszczonych porów, których kształt i orientacja wynika z zastosowanej metody wstępnego zagęszczania ,,surowego” materiału przed spiekaniem.
W literaturze parametr Grüneisena przyjęło się oznaczać literą \(\gamma\), aby jednak uniknąć dwuznaczności (poprzez \(\gamma\) oznaczona została wcześniej energia powierzchniowa), parametr ten został dodatkowo opatrzony indeksem \(_{\text{G}}\) (\(\gamma_{\text{G}}\)).↩︎
Dla kryształów, składowe tensora rozszerzalności cieplnej \(\alpha_{ij}\) nazywane są również głównymi albo osiowymi współczynnikami rozszerzalności cieplnej i są oznaczane poprzez indeksy odpowiadające wybranym osiom czworościanu zasadniczego jako \(\alpha_a\), \(\alpha_b\) i \(\alpha_c\).↩︎
Postać odpowiednich macierzy reprezentujących tensor rozszerzalności cieplnej dla wymienionych układów krystalograficznych, można znaleźć w wielu opracowaniach z zakresu mechaniki, krystalografii i inżynierii materiałowej [49, 138].↩︎
Poznanie, zrozumienie i opis budowy tworzyw ceramicznych w mikroskali, są istotne nie tylko ze względu na możliwość kontroli procesu wytwarzania, ale przede wszystkim z uwagi na silną zależność między mikrostrukturą a końcowymi właściwościami materiału w makroskali. Związek ten stanowi jeden z głównych paradygmatów inżynierii materiałowej, w myśl którego: racjonalne kształtowanie budowy materiału na poziomie mikrostruktury, daje możliwość efektywnej modyfikacji jego właściwości użytkowych.
Wymienione do tej pory cechy tworzyw ceramicznych, takie jak: zróżnicowana mikrostruktura, obecność porów, duża sztywność czy katastrofalne, kruche pękanie, inicjowane obecnością wad, wpływają bezpośrednio lub pośrednio na specyficzne właściwości tej grupy materiałów i wymagają szerokiego zestawu parametrów ilościowych, niezbędnych do ich opisu. Dodatkowo wzajemne powiązanie niektórych cech, a tym samym parametrów je opisujących, komplikuje formułowanie uniwersalnych zależności między mikrostrukturą a właściwościami. Opierając się jednak na bogatym materiale doświadczalnym, gromadzonym przez wiele dziesięcioleci, ustalone zostały empiryczne związki, co do których panuje konsensus. Najważniejsze z nich zostaną omówione w kolejnych punktach.
Wpływ rozmiaru krystalitów 14 na wytrzymałość, jest jednym z takich związków między mikrostrukturą a właściwościami, które są dobrze udokumentowane i intensywnie analizowane. Wyniki pomiarów przeprowadzonych dla wielu materiałów ceramicznych wskazują, że materiały posiadające drobnoziarnistą mikrostrukturę uzyskują zwykle wyższą wytrzymałość (\(\sigma_{\text{f}}\)) od materiałów gruboziarnistych. Tę empiryczną regułę można zilustrować wykresem \(\sigma_{\text{f}}\) od odwrotności pierwiastka kwadratowego z rozmiaru krystalitów (\(D^{-1/2}\)). Takie zestawienie danych pozwala na analizę zmienności \(\sigma_{\text{f}}\) dla pełnego zakresu rozmiaru krystalitów, uwzględniającego również wytrzymałość monokryształów (w takim zestawieniu przyjmuje się, że dla monokryształów \(D\) ma bardzo duże wartości, więc \(D^{-1/2} \rightarrow 0\)). Zależność \(\sigma_{\text{f}}\) od \(D^{-1/2}\) dla materiałów ceramicznych została przedstawiona na rys. 1.4.
W temperaturze pokojowej, przy założeniu, że efekty wywołane innymi czynnikami (porowatością, kształtem ziaren, obecnością fazy szklistej) nie będą istotnie wpływać na rozpatrywaną zależność, można zauważyć, że dla materiałów gruboziarnistych (lewa gałąź wykresu na rys. 1.4) wzrost rozmiaru krystalitów prowadzi do wyraźnego obniżenia wytrzymałości, aż do wartości zbliżonych do wytrzymałości monokryształów (\(\sigma_{\text{f}}^{\text{mono}}\)). W materiałach, dla których granica plastyczności ma stosunkowo niską wartość (jak na substancje jonowo-kowalencyjne) i występuje w nich duża liczba systemów poślizgu, mechanizm niszczenia inicjowany jest mikroplastycznością [50, 139]. Do takich materiałów należą halogenki litowców i tlenki berylowców, czyli związki o przeważającym charakterze jonowym wiązań chemicznych, tworzące kryształy z układu regularnego (grupy przestrzennej \(Fm\overline{3}m\)) o strukturach typu Halitu (\(\text{NaCl}\), \(\text{KCl}\), \(\text{KBr}\), \(\text{CsI}\), \(\text{LiF}\), \(\text{MgO}\), \(\text{CaO}\)), jak również typu Fluorytu (\(\text{CaF}_{\text{2}}\), \(\text{UO}_{\text{2}}\)) [37, 140] (por. tab. [tab:MatCeramKryszt]).
Mechanizm niszczenia mający źródło w mikroplastyczności można opisać równaniem Halla–Petcha [141, 142]: \[\label{eq:Hall-Petch} \sigma_{\text{Y}}= \sigma_{\text{Y0}}+ \frac{k_{\text{Y}}}{\sqrt{D}},\] w którym: \(\sigma_{\text{Y}}\) jest naprężeniem uplastyczniającym, \(\sigma_{\text{Y0}}\) – naprężeniem ścinającym, wymaganym do uruchomienia dyslokacji dla najłatwiejszego (wymagającego najniższego naprężenia) systemu poślizgu, które w przybliżeniu jest równe granicy plastyczności monokryształu, oraz \(k_{\text{Y}}\) jest współczynnikiem umocnienia, charakterystycznym dla danego materiału i opisującym oddziaływanie granic międzyziarnowych na ruch dyslokacji.
Jeśli zatem w rozważanych materiałach posiadających niską wartość granicy plastyczności, pojawią się naprężenia równe, bądź większe, od \(\sigma_{\text{Y}}\), to zainicjują one lawinowy ruch dyslokacji odpowiedzialny za mechanizm mikroplastycznego niszczenia materiału. Poniżej pewnego rozmiaru krystalitów – w gałęzi drobnoziarnistej (po prawej stronie wykresu na rys. 1.4), naprężenia potrzebne do uruchomienia mechanizmu mikroplastycznego stają się jednak zbyt duże. Dlatego do zniszczenia dochodzi wtedy za sprawą istniejących w materiale wad, będących wynikiem niecałkowitego zagęszczenia (porowatości) czy obecności zanieczyszczeń, kumulujących się w granicach międzyziarnowych.
Taki mechanizm nie jest jednak typowy dla materiałów ceramicznych – a w szczególności dla ceramiki specjalnej. Zwykle granica plastyczności w temperaturze pokojowej ma na tyle dużą wartość, że nie obserwuje się uplastycznienia zapoczątkowującego zniszczenie. Wynika to z niższej symetrii krystalitów, a tym samym z mniejszej liczby niezależnych systemów poślizgu, oraz większego udziału charakteru kowalencyjnego wiązań pomiędzy atomami, co wyraźnie podnosi wartość naprężeń wymaganych do uruchomienia poślizgu dyslokacji 15. Dlatego do opisu mechanizmu niszczenia tego typu materiałów wykorzystuje się model kruchego pękania.
W modelu tym przyjmuje się, że mechanizm powodujący wzrost wytrzymałości przy zmniejszających się wymiarach ziaren, związany jest z uprzednio istniejącymi w materiale wadami. Źródłem takich wad mogą być wymienione już pory, zanieczyszczenia, ale również ziarna wtrąceń, mikropęknięcia i wiele innych (wady strukturalne i technologiczne). Jednak najbardziej istotnymi, wydają się wady powierzchniowe, powstające podczas technologicznej obróbki wykańczającej – w warunkach laboratoryjnych, w trakcie przygotowania powierzchni próbek do pomiarów. Wady takie mają zwykle wymiary 16 od kilku do kilkudziesięciu mikrometrów i zależą głównie od metody wykańczania powierzchni, a w znacznie mniejszym stopniu od rozmiaru ziaren [139].
Niezależnie od źródeł wad, ich rozmiar może być zarówno mniejszy niż ziaren, jak i obejmować swoim zasięgiem obszar kilku ziaren. Dlatego mechanizm niszczenia jest nieco inny dla gałęzi grubo- i drobnoziarnistej. Jeśli zatem wada jest mniejsza niż ziarno i znajduje się w jego wnętrzu, to zewnętrzne obciążenia mogą spowodować jej rozrost, aż do momentu w którym wierzchołek pęknięcia napotka granicę międzyziarnową (rys. 1.5a). Jeśli z kolei wada o niewielkich wymiarach znajduje się w granicy międzyziarnowej, jej rozprzestrzenianie będzie przebiegało wzdłuż tej granicy – również do momentu, w którym wierzchołek pęknięcia dotrze do granicy kolejnego ziarna (rys. 1.5b). W obydwu przypadkach propagująca szczelina, na dystansie zbliżonym do rozmiaru ziarna, napotyka tylko na niewielki opór charakterystyczny dla monokryształu albo granicy międzyziarnowej. Dalszy, niestabilny wzrost długości szczeliny wymaga większego nakładu energii, która jest niezbędna do pokonania bariery, jaką stanowią granice międzyziarnowe ułożone pod dużym kątem względem kierunku jej propagacji. Dodatkowo, dla krystalitów o strukturze innej niż regularna, występująca w nich anizotropia rozszerzalności cieplnej i sprężystości, mogąca prowadzić do lokalnej kumulacji naprężenia rozciągającego, może ułatwiać dalsze rozprzestrzenianie się pęknięcia przez sąsiednie ziarna [144–146]. Podsumowując, można więc przyjąć, że niszczenie materiału w gałęzi gruboziarnistej, jest determinowane wadami krytycznymi o promieniu \(c\), którego wartości mieszczą się w przedziale od \(\frac{1}{2}D\) do \(3D\).
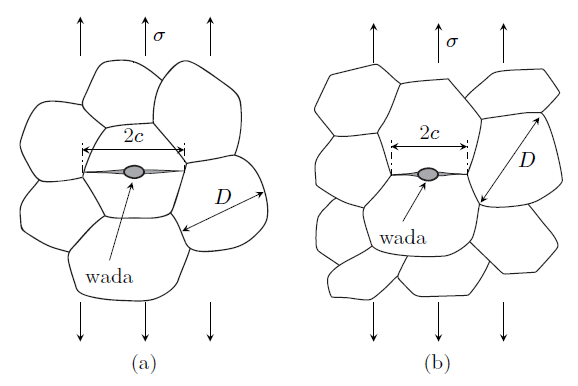
W drobnoziarnistej gałęzi (rys. 1.4), istniejące w materiale wady są zwykle dużo większe od rozmiaru krystalitów i dlatego wytrzymałość praktycznie nie zależy od \(D\). W takim przypadku, podstawowym czynnikiem limitującym wytrzymałość litych tworzyw ceramicznych, staje się rozmiar wad, szczególnie powierzchniowych, powstałych w wyniku obróbki wykańczającej [50].
Intensywnie prowadzone prace w zakresie technologi materiałów ceramicznych, dotyczące zarówno preparatyki proszków jak i metod syntezy [42, 147–152], doprowadziły do obniżenia rozmiaru ziaren w litych tworzywach poniżej 0.1 μm. W praktyce, przekroczenie tej granicy i uzyskanie nanometrycznej mikrostruktury, wiąże się często z kompromisem pomiędzy zachowaniem minimalnego rozmiaru krystalitów, a porowatością, która istotnie obniża wytrzymałość [139, 153]. Problem ten stanowi nadal wyzwanie technologiczne i jest przedmiotem ciągłych badań [53, 152, 154–157]. Dlatego zależność pomiędzy rozmiarem ziaren a wytrzymałością w przypadku nanomateriałów ceramicznych, nie jest jeszcze do końca wyjaśniona, a obecność i rola konkretnych mechanizmów, obserwowanych w różnych grupach materiałów, pozostaje otwarta [53, 152, 153, 158]. Należy jednak zauważyć, że lite nanomateriały ceramiczne wykazują unikalne właściwości. Przykładowo, w porównaniu do polikryształów zawierających ziarna mikronowe i submikronowe, tworzywa o ziarnach nanometrycznych mogą wykazywać znaczną ciągliwość przed zniszczeniem. Zjawisko to pojawia się, gdy rozmiary ziaren są mniejsze niż 50 nm i jest tłumaczone poślizgiem występującym w granicach międzyziarnowych. W takim mechanizmie istotna staje się ruchliwość atomów, która skutkuje plastycznością, podobną do obserwowanej w metalach [53, 153, 159].
Ponieważ krystality są bryłami o nieregularnych kształtach, to określenie ich rozmiaru poprzez podanie wymiaru charakterystycznego, np. średnicy, wymaga przyjęcia konwencji, opierającej się na przybliżeniu kształtu krystalitu, prostą figurą geometryczną. Parametry opisujące mikrostrukturę zostaną przedstawione w rozdz. 2.2.1.↩︎
Dla tlenku glinu (korundu) \(\sigma_{\text{Y0}}\) w temperaturze pokojowej wynosi 15.4 GPa, a dla węglika krzemu 21.1 GPa [143].↩︎
Rozmiar wady opisywany jest zwyczajowo, zgodnie z teorią Griffitha, promieniem i dla wady krytycznej oznaczany jest jako \(c\).↩︎
Ziarna budujące polikrystaliczne tworzywa ceramiczne mogą przybierać złożone formy (por. rys. 1.1), które w trakcie ilościowej analizy mikrostruktury opisywane są szeregiem specyficznych parametrów kształtu. Podobnie jak podczas określania rozmiaru, stosowane są uproszczenia geometryczne, pozwalające na przybliżenie rzeczywistej morfologii analizowanych niejednorodności, prostymi figurami geometrycznymi – wzorcami, których kształt można zdefiniować podając niewielki zestaw parametrów: średnicę, długość boku, wysokość, szerokość, kąt między ścianami itp. Odpowiadające tym parametrom, bezwymiarowe współczynniki kształtu, określają zwykle stopień odstępstwa kształtu rzeczywistego ziarna, od kształtu przyjętego wzorca 17. Taki szczegółowy opis, specyficzny dla wybranego rodzaju mikrostruktury, komplikuje jednak formułowanie ogólnych zależności, którym poświęcony jest ten rozdział. Dlatego zostanie tutaj wykorzystany opis jakościowy, opierający się na przybliżeniu kształtu ziaren jednym z kilku typowych pokrojów, charakterystycznych dla monokryształów. Ziarna przybliżane będą zatem kształtem kolumnowym, izometrycznym lub płytkowym. W materiałach wielofazowych, w których podczas spiekania obecna jest faza szklista, oraz w wielu kompozytach ceramicznych, przybliżenie takie pozwala zwykle na efektywny opis obserwowanej mikrostruktury. Większe odstępstwa od przyjętych wzorców pojawiają się w materiałach jednofazowych, składających się z krystalitów o nieregularnych kształtach.
O ile rozpatrywaną wcześniej zależność, między rozmiarem ziaren a wytrzymałością polikrystalicznych tworzyw ceramicznych, można uznać za uniwersalną, to kształt ziaren staje się istotny jedynie dla ograniczonej grupy materiałów. Krystality muszą więc wykazywać anizotropię, co w praktyce oznacza, że powinny mieć strukturę inną niż regularna. Jest to warunek konieczny do tego, aby można było oczekiwać makroskopowych różnic we właściwościach wynikających z kształtu ziaren. Dodatkowo, jak już wcześniej wspomniano, makroskopowe efekty mogą wynikać bezpośrednio z analizowanego parametru, jak również powstawać na skutek złożonych interakcji pomiędzy wieloma czynnikami. Rozważając jedynie bezpośredni wpływ kształtu, należy zatem dodatkowo przyjąć, że rozpatrywane ziarna powinny mieć pokrój zbliżony do kolumnowego lub płytkowego. Co prawda, izometryczne, anizotropowe ziarna mogą wpływać na właściwości tworzywa, np. poprzez resztkowe naprężenia cieplne, jest to jednak już efekt pośredni, którego intensywność jest specyficzna dla konkretnego materiału.
Kolejną kwestią, która wymaga ustalenia, jest orientacja – zarówno wewnętrzna, związana z ułożeniem osi i płaszczyzn krystalograficznych względem ścian krystalitu, jak i względna, wynikająca z lokalnego ułożenia sąsiadujących ziaren oraz globalna rozpatrywana w odniesieniu do wymiarów zewnętrznych próbki. W materiałach ceramicznych, wewnętrzna orientacja krystalograficzna jest zwykle powiązana z kształtem ziaren [160]. Przykładem występowania takiej korelacji mogą być kolumnowe, heksagonalne krystality \(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\), których oś jest równoległa do kierunku \([001]\), czy płytkowe krystality \(\alpha\text{-SiC}\), rozrośnięte w płaszczyźnie \((001)\) [161–164].
Ograniczając się zatem do nieizometrycznych ziaren, które mogą bezpośrednio wpływać na właściwości tworzywa, można przyjąć, że rozkład statystyczny ich orientacji przestrzennej w polikrysztale ceramicznym, z dobrym przybliżeniem będzie odpowiadał rozkładowi statystycznemu orientacji krystalograficznej, a tym samym, decydował o ewentualnej makroskopowej anizotropii polikryształu. Inaczej mówiąc, jeśli w materiale ułożenie płytkowych lub wydłużonych ziaren nie będzie całkowicie przypadkowe – pojawi się preferowany kierunek lub płaszczyzna – to makroskopowe właściwości będą wykazywać anizotropię. Zjawisko takie można wywołać na etapie przygotowania i formowania ,,surowej” masy ceramicznej (przygotowanie granulatu, prasowanie, formowanie plastyczne, odlewanie) i, w mniejszym zakresie, podczas końcowego procesu zagęszczania (techniki prasowania na gorąco) [13, 139, 165]. W efekcie uzyskane, lite tworzywo posiadać będzie ukierunkowaną orientację krystalitów, która w połączeniu ze specyficznym kształtem porów, powoduje anizotropię wielu właściwości: mechanicznych, cieplnych, elektrycznych czy optycznych [37, 139, 166, 167].
Obecna w takich tworzywach tekstura może jednak powodować szereg niekorzystnych efektów. Ich źródłem są naprężenia cieplne, powstające w trakcie studzenia po wysokotemperaturowym etapie spiekania. Z uwagi na ograniczoną plastyczność ceramiki, nierównomierny skurcz anizotropowych ziaren wywołany obniżeniem temperatury, prowadzi do kumulacji energii odkształceń cieplnych. Takie, silnie naprężone krystality mogą więc rozpraszać energię poprzez pękanie. Powstające w ten sposób mikrospękania obniżają wytrzymałość, a niekiedy powodują zniszczenie tak uformowanego materiału 18.
Dlatego podczas wytwarzania materiałów konstrukcyjnych, w których decydującą rolę odgrywają właściwości mechaniczne, dąży się do ujednorodnienia rozkładu orientacji przestrzennej krystalitów. W takim przypadku istotne staje się lokalne, względne ułożenie wydłużonych lub płytkowych ziaren. Jeśli dominującym sposobem dekohezji materiału jest pękanie międzyziarnowe, to kształt ziaren może efektywnie poprawiać odporność na pękanie [8, 139, 145, 168]. Udział pękania międzyziarnowego w stosunku do wskrośziarnowego zależy od względnej wytrzymałości granic międzyziarnowych i ziaren (rys. 1.6). W materiałach wielofazowych, kompozytach ale również w jednofazowych polikryształach, w których granice międzyziarnowe charakteryzują się mniejszą energią wymaganą na rozprzestrzenianie się pęknięcia, obserwowane są mechanizmy umocnienia analogiczne do obecnych w klasycznych kompozytach wzmacnianych włóknami. Występuje więc mostkowanie pęknięć (ang. crack bridging) i wyciąganie ziaren (ang. pullout), ale również inne mechanizmy odpowiedzialne za wzrost odporności na pękanie, takie jak odchylanie pęknięć (ang. crack deflection), klinowanie pęknięć (ang. crack roughness), które działając łącznie odpowiadają za wzrost wartości \(K_{\text{Ic}}\) [139, 169].

Szczególnie dobrze udokumentowane jest umocnienie występujące w azotku krzemu (\(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\)), spiekanym w obecności fazy tlenkowej. W wielu pracach zaobserwowany został nawet trzykrotny wzrost wartości \(K_{\text{Ic}}\) – od wartości 3 MPa m1/2 dla tworzyw o izometrycznych ziarnach \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), do 12 MPa m1/2 w przypadku obecności ziaren silnie wydłużonych [171–174]. Ponadto w tworzywach tych, istotna jest również rola fazy tlenkowej, w której z uwagi na wyższą wartość współczynnika rozszerzalności cieplnej w porównaniu do oddzielanych przez nią ziaren \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), pojawiają się resztkowe naprężenia cieplne, mogące inicjować mikrospękania. Obecność takich nieciągłości w granicznej fazie tlenkowej, osłabia ją, a tym samym zwiększa udział pękania międzyziarnowego [175–178]. Podobne umocnienie opisywane jest również w przypadku węglika krzemu spiekanego z fazą tlenkową [179, 180] czy tlenku glinu spiekanego w obecności aktywatorów [26, 181–183], jak również w ceramicznych kompozytach ziarnistych [144, 184–187].
Efektywność poszczególnych mechanizmów umocnienia, zależy od parametrów wewnętrznych – właściwości faz, ale również od czynników geometrycznych, wynikających z mikrostruktury tworzywa. W przypadku gdy krystality są silnie wydłużone, dominującym mechanizmem staje się mostkowanie – ziarna zachowują się w podobny sposób do wiskerów. Jeśli natomiast wydłużenie jest niewielkie, efektywność mostkowania maleje i zaczyna dominować mechanizm polegający na odchylaniu pęknięć [8, 50, 139].
Mechanizm ten został ilościowo opisany przez Faber i Evansa [188, 189]. Ich rozważania teoretyczne dotyczyły wpływu różnych czynników na rozwój pęknięcia, w kompozycie ziarnistym. Analizie został poddany wpływ udziału objętościowego wtrąceń o różnym kształcie – sferycznym, kolumnowym o przekroju kolistym, płytkowym w formie dysków, przy uwzględnieniu współczynnika kształtu i odległości między wtrąceniami. Siłę napędową powodującą rozprzestrzenianie się pęknięcia, wyrażoną poprzez krytyczną szybkość uwalniania energii odkształceń \(G\) \eqref{eq:G_2gamma} opisali oni jako: \[\label{eq:FaberEvans_G} EG = k_1^2(1-\nu^2) + k_2^2(1-\nu^2) + k_3^2(1-\nu^2),\] przy czym \(k_1\), \(k_2\), \(k_3\) są lokalnymi współczynnikami intensywności naprężeń dla trzech typów obciążeń, a \(E\) oraz \(\nu\) to moduły sprężystości.
W przypadku rozwierania szczeliny dla pierwszego typu obciążenia (rys. 1.7), lokalne współczynniki dla odchylonej o kąt \(\theta\) szczeliny (\(k_1^t\) i \(k_2^t\)) można powiązać z globalnym współczynnikiem intensywności naprężeń: \[\label{eq:FaberEvans_kt} k_1^t = a_{11}(\theta)K_{\text{I}}, \qquad k_2^t = a_{21}(\theta)K_{\text{I}},\] gdzie \(a_{11}\) i \(a_{21}\) są funkcjami kątowymi określonymi przez Cotterella i Rice’a [188, 190]: \[\label{eq:CotterellRice_kTilt} a_{11}(\theta) = \cos^3(\theta/2), \qquad a_{21} = \sin(\theta/2)\cos^2(\theta/2).\]
Lokalne współczynniki intensywności naprężeń dla frontu szczeliny, która po odchyleniu o kąt \(\theta\), zostaje następnie skręcona o kąt \(\phi\) (rys. 1.7), można więc wyrazić poprzez wcześniej określone współczynniki \(k_1^t\) i \(k_2^t\) [188, 190]: \[\label{eq:FaberEvans_kTwist} k_1^{T} = a_{11}(\phi)k_1^t + a_{12}(\phi)k_2^t, \qquad k_3^{T} = a_{31}(\phi)k_1^t + a_{32}(\phi)k_2^t,\] gdzie \(a_{11}(\phi)\), \(a_{12}(\phi)\), \(a_{31}(\phi)\) i \(a_{32}(\phi)\) są funkcjami dla kąta skręcenia 19 .
Rozwiązanie powyższych równań, wymaga jednak przyjęcia pewnej statystyki, opisującej rozkład kątów odchylania \(\theta\) i skręcania \(\phi\). Opierając się na zależnościach stereologicznych podanych przez Fullmana [191], Faber i Evans określili związki między umocnieniem a udziałem objętościowym \(V_f\) i parametrami opisującymi kształt wtrąceń. Dla kolejnych kształtów, rozwiązania te można zapisać równaniami [188]: \[\label{eq:FaberEvansSfer} \frac{G_c^{\text{sfer}}}{G_c^o} = 1 + 0.87V_f,\] \[\label{eq:FaberEvansRods} \frac{G_c^{\text{kol}}}{G_c^o} = 1 + \left[0.6 + 0.007\frac{h}{r} - 0.0001 \left(\frac{h}{r}\right)^2\right]V_f,\] \[\label{eq:FaberEvansDisks} \frac{G_c^{\text{dysk}}}{G_c^o} = 1 + 0.56 \frac{r}{t}V_f,\] w których \(G_c^{\text{sfer}}/G_c^o\), \(G_c^{\text{kol}}/G_c^o\), \(G_c^{\text{dysk}}/G_c^o\) wyrażają względne, krytyczne szybkości uwalniania energii odkształceń dla kompozytów zawierających kolejno wtrącenia: sferyczne, kolumnowe i dyskowe, w stosunku do krytycznej szybkości uwalniania energii w osnowie. Ułamki \(h/r\) i \(r/t\) są współczynnikami kształtu, określającymi odpowiednio: stosunek długości do promienia kolumny oraz stosunek promienia do grubości dysku.
Przyjęcie w przedstawionym rozwiązaniu statystyk, opisujących rozkład kątów \(\theta\) i \(\phi\) wynikających jedynie z zależności stereologicznych, nie uwzględnia ograniczeń geometrycznych, które mogą wynikać z bliskiego sąsiedztwa wtrąceń. Dlatego powyższe równania dobrze opisują umocnienie dla niewielkiego udziału objętościowego \(V_f\). Jeśli udział ten jest większy (\(V_f > 0.2\)), należy uwzględnić ograniczenia geometryczne dla kątów \(\theta\) i \(\phi\). Odpowiednie, zmodyfikowane równania można znaleźć w pracy Faber i Evansa [188].
Przedstawione rozumowanie, sformalizowane przy pomocy równań \eqref{eq:FaberEvansSfer}\eqref{eq:FaberEvansRods}\eqref{eq:FaberEvansDisks}, pozwala dodatkowo na sformułowanie ogólnych wniosków dotyczących wpływu kształtu ziaren na mechanizm umocnienia związany z odchylaniem pęknięć [50]:
Wzrost odporności na kruche pękanie, spowodowany odchylaniem pęknięcia, zależy od kształtu i udziału objętościowego wtrąceń, ale nie zależy od ich rozmiaru.
Najskuteczniej zwiększają odporność na pękanie wtrącenia w kształcie kolumnowym (pręty), nieco słabiej płytkowym (dyski), a najsłabiej wtrącenia izometryczne (kule). W przypadku prętów, efekt umocnienia wzrasta wraz ze wzrostem wartości współczynnika kształtu, aż do wartości \(h/r \approx 12\).
Odporność na pękanie wyraźnie wzrasta wraz z rosnącą wartością ułamka objętościowego odchylających wtrąceń – aż do \(V_f \approx 0.2\); powyżej tej wartości, wzrost odporności na pękanie jest już nieznaczny.
Maksymalny wzrost odporności na kruche pękanie, spowodowany przez pręty o \(h/r = 12\) i \(V_f = 0.2\), jest około czterokrotnie większy od odporności na pękanie materiału bez cząstek odchylających – gdy jest on wyrażony poprzez krzywą \(R\) (czyli w kategoriach energetycznych) lub około dwukrotnie większy, gdy wyrażony jest poprzez krzywą \(T\) (czyli poprzez intensywność naprężeń).
Powyższe wnioski wskazują zatem, że efektywność mechanizmu odchylania jest szczególnie wysoka dla ziaren silnie wydłużonych. Pomimo tego, obserwowane w takim przypadku umocnienie, przypisywane jest głównie mechanizmowi mostkowania, którego udział w całkowitej energii pękania jest dominujący [192, 193]. Kształt ziaren, a właściwie ich wydłużenie, ma w mechanizmie mostkowania aspekt kryterialny. Przy dużej wartości współczynnika kształtu, mechanizm ten, i związany z nim mechanizm wyciągania, opisywany jest tak jak w przypadku włókien ciągłych czy wiskerów zdyspergowanych w osnowie. Istotna jest więc głównie długość i średnica cząstek tworzących mostki.
Mechanizm mostkowania dla wiskerów został opisany przez Bechera i in. [194]. Wzrost szybkości uwalniania energii \(\Delta G\), odpowiedzialny za umocnienie, można wyrazić więc poprzez sumę energii sprężystej skumulowanej w mostkach \(\mathop{}\!\mathrm{d}U_{\text{e}}\) i pracy potrzebnej na ich wyciąganie \(\mathop{}\!\mathrm{d}W_{\text{s}}\) [194]: \[\label{eq:Becher1988int} \Delta G = 2N \int\limits_{0}^{l_{\text{db}}}(\mathop{}\!\mathrm{d}U_{\text{e}}+ \mathop{}\!\mathrm{d}W_{\text{s}}),\] gdzie: \(N\) jest liczbą wiskerów przypadającą na jednostkę powierzchni (\(N=V_f/(\pi r^2)\)), a \(l_{\text{db}}\) to długość fragmentu wiskera, na której zachodzi proces wyciągania (rys. 1.8). Składniki sumy energii można opisać wyrażeniami [194]: \[\label{eq:BecherU} \mathop{}\!\mathrm{d}U_{\text{e}}= \frac{2\pi\left( l_{\text{db}} - y \right)^2 \tau_{\text{i}}^2 \mathop{}\!\mathrm{d}y}{E_w},\] \[\label{eq:BecherW} \mathop{}\!\mathrm{d}W_{\text{s}} = 2\pi r \tau_{\text{i}} u \mathop{}\!\mathrm{d}y,\] w których \(\tau_{\text{i}}\) jest maksymalnym naprężeniem ścinającym, mogącym działać na powierzchni wiskera (wytrzymałością granicy międzyziarnowej na ścinanie) o module sprężystości oznaczonym przez \(E_w\), a \(y\) jest aktualną długością rozwarstwienia między wiskerem a osnową (\(0 < y < l_{\text{db}}\)), powstającego na skutek przemieszczenia fragmentu wiskera względem osnowy o \(u = (l_{\text{db}} - y)^2 \tau_{\text{i}}/ (E_w r)\). Ostatecznie, całkowanie równania \eqref{eq:Becher1988int} po uprzednim podstawieniu wyrażeń \eqref{eq:BecherU}\eqref{eq:BecherW}, pozwala przedstawić wzrost szybkości uwalniania energii w postaci: \[\label{eq:Becher1988dG} \Delta G = \frac{4 V_f \tau_{\text{i}}^2 l_{\text{db}}^3}{3 E_w r^2}.\]
Na podstawie powyższego równania można zatem stwierdzić, iż umocnienie wywołane mostkowaniem, w przypadku silnie wydłużonych ziaren, istotnie zależy od ich długości \(l\), która ogranicza obszar wyciągania (\(2 l_{\text{db}} \leqslant l\)), a tym samym przestrzeń, w której zachodzi rozpatrywany proces. Aby zatem zmaksymalizować efekt mostkowania, wtrącenia powinny charakteryzować się możliwie dużymi wartościami współczynnika kształtu, czyli posiadać dużą długość przy niewielkiej wartości promienia. Warto również zauważyć, że zwiększanie wytrzymałości na ścinanie granicy między cząstką a osnową (\(\tau_{\text{i}}\)), może doprowadzić do zmiany typu pękania – z międzyziarnowego na wskrośziarnowy – co osłabia, a nawet całkowicie eliminuje efekt mostkowania. Maksymalne umocnienie może być więc osiągnięte, gdy wytrzymałość wiskerów \(\sigma_{\text{f}}^{\text{w}} = 2 l_{\text{db}} \tau_{\text{i}} / r\) [50, 194]. Dodatkowo na mechanizm mostkowania, a w szczególności na \(\tau_{\text{i}}\), istotny wpływ mają naprężenia cieplne, wynikające z różnic, albo anizotropii, rozszerzalności cieplnej ziaren. Mogą one prowadzić do koncentracji naprężeń, a niekiedy do powstawania mikrospękań, zlokalizowanych głównie w granicach międzyziarnowych [149, 194, 195]. Ponadto, w trakcie wyciągania ziaren z osnowy, odpowiadają one za naprężenie ścinające (\(\tau_{\text{i}}\)), występujące na przemieszczających się względem siebie powierzchniach [196]: \[\label{eq:tarcie_pull} \tau_{\text{i}} = \tau_0 + \mu \sigma_r,\] gdzie: \(\tau_0\) jest naprężeniem ścinającym wynikającym z chropowatości, \(\mu\) współczynnikiem tarcia, a \(\sigma_r\) radialną składową naprężeń cieplnych – prostopadłą do powierzchni trących.
W przypadku krótkich wiskerów, a tym bardziej izometrycznych ziaren, w których współczynnik kształtu zbliża się do jedności, mechanizm oparty na wyciąganiu nie jest już tak efektywny. Mostkowanie uzupełniane jest mechanicznym klinowaniem ziaren, spinających powierzchnie szczeliny (ang. grain interlocking) [92, 197, 198] (rys. 1.9). Ziarna takie, zorientowane przypadkowo względem kierunku propagacji pęknięcia, w trakcie rozwierania szczeliny, ulegają rotacji o kąt \(\theta\) – blokowanej przez sąsiednie ziarna i przemieszczaniu – któremu przeciwdziała tarcie (\(\mu\sigma_n\)).
Pracę dla pojedynczego ziarna \(w_{\text{g}}\), niezbędną do wywołania wymienionych efektów, można opisać równaniem wyprowadzonym dla modelowego układu przez Vekinis i in. [199]: \[\label{Vekinis1990work} w_{\text{g}} = 2 \mu \sigma_n a d_{\text{min}}^2 l \theta,\] w którym \(\sigma_n\) jest naprężeniem normalnym do przemieszczających się powierzchni, \(a\) określa udział stykających powierzchni (\(0 < a < 1\)), \(d_{\text{min}}\) jest mniejszym wymiarem ziarna, a \(l\) wyraża ramię momentu skręcającego ziarno (\(l \approx d_{\text{max}}/2\), przy czym \(d_{\text{max}}\) jest większym wymiarem ziarna). Dla \(N\) mostków przypadających na jednostkę powierzchni, można zatem określić wzrost szybkości uwalniania energii jako [199]: \[\label{Vekinis1990DG} \Delta G = N\!w_{\text{g}}.\] Przybliżając kształt ziarna elipsą, o długości osi wielkiej i małej, równych odpowiednio \(d_{\text{max}}\) i \(d_{\text{min}}\), której powierzchnia jest równa \(\pi d_{\text{max}} d_{\text{min}} / 4\), można wyrazić \(N\) poprzez udział powierzchniowy mostków (\(f\)), jako stosunek: \(N = 4f/(\pi d_{\text{max}} d_{\text{min}})\). Przyjmując dodatkowo, że średnia wartość kąta rotacji \(\theta = \pi/4\) (średnia ze wszystkich możliwych rotacji między 0 a \(\pi/2\)) oraz \(a \approx 1/4\), można uzupełnić równanie \eqref{Vekinis1990DG} i zapisać zmianę szybkości uwalniania energii wywołaną klinowaniem ziaren w postaci: \[\label{Vekinis1990} \Delta G = \frac{d_{\text{min}}}{4} f \mu \sigma_n.\]
Przeprowadzone na podstawie powyższego równania oszacowanie dla polikrystalicznego tlenku glinu, dla którego Vekinis i in. [199] przyjęli: \(\sigma_n =\)400 MPa, \(\mu =\)0.6, \(d_{\text{min}} =\)5 μm i \(\Delta G =\)30 J/m2, wskazuje, że wartość \(f\), niezbędna do uzyskania zakładanego umocnienia, wynosi \(\sim\)0.1. Ujmując to inaczej, jeśli choć jedno na dziesięć ziaren, leżących na drodze propagacji pęknięcia, będzie uczestniczyło w mostkowaniu zgodnie z przyjętym modelem, to zapewni ono umocnienie odpowiadające rzeczywistemu – obecnemu w analizowanym materiale. Wniosek ten wskazuje, że klinowanie może być istotnym składnikiem podnoszącym odporność na pękanie w litych materiałach polikrystalicznych. Dokładna analiza tego mechanizmu wskazuje również, że naprężenia cieplne mogą znacząco podnosić wartość \(\Delta G\) poprzez ich bezpośredni wpływ na wartość \(\sigma_n\). Jest to szczególnie widoczne w materiałach o symetrii krystalitów innej niż regularna [50, 139, 195].
Dodatkowym zjawiskiem, które nie zostało uwzględnione w powyższym opisie, a które występuje często wraz z mechanicznym blokowaniem, jest powstawanie lokalnej siatki mikrospękań 20. Tworzy się ona zwykle w pobliżu propagującej szczeliny i jest skutkiem nakładania się naprężeń cieplnych skumulowanych w materiale z naprężeniami powstającymi wskutek oddziaływania spinających powierzchnię szczeliny ziaren z ziarnami otaczającymi je [50, 199, 201–203].
Przedstawione modele analityczne, ujmujące wpływ kształtu i orientacji ziaren na odporność na pękanie opierają się na szeregu założeń i uproszczeń, pozwalających na zwięzły opis rozpatrywanych zjawisk. Obserwacje mikrostruktury litych, polikrystalicznych materiałów ceramicznych, wskazują jednak, że rzeczywista morfologia ziaren jest istotnie zróżnicowana. Abstrahując od kształtu krystalitów, który zwykle odbiega od kształtu wyidealizowanych wzorców stosowanych w analitycznym ujęciu, nawet podstawowe parametry mikrostruktury, takie jak średnica równoważna czy współczynnik kształtu, wymagają do ich ilościowego opisu stosowania rozkładów statystycznych. Dlatego modele mikromechaniczne wykorzystywane do analizy właściwości materiału, uwzględniającej kształt ziaren, opierają się coraz częściej na metodach przybliżonych. Stosowane są w tym celu dwu- lub trójwymiarowe modele geometryczne, odwzorowujące rzeczywistą albo syntetyczną mikrostrukturę materiału. W połączeniu ze statystycznym opisem morfologii i topologii polikryształów, pozwalają one na szczegółowe badanie właściwości rzeczywistych tworzyw [19, 204–210].
Informacje na temat stosowanych do opisu mikrostruktury parametrów kształtu zostały zawarte w rozdziale 2 (p. 2.2.2).↩︎
Wpływ naprężeń cieplnych na właściwości mechaniczne tworzyw ceramicznych jest złożony i przy odpowiednim doborze faz składowych oraz mikrostrukturze może odpowiadać również za wzrost odporności na pękanie. Zjawisko to zostanie szerzej opisane w rozdz. 1.4.↩︎
Algebraiczną postać funkcji \(a_{11}(\phi)\), \(a_{12}(\phi)\), \(a_{31}(\phi)\) i \(a_{32}(\phi)\) można znaleźć w cytowanych pracach Cotterella i Rice’a [190] oraz Faber i Evansa [188].↩︎
Obecność porów w litych tworzywach ceramicznych jest jedną z charakterystycznych cech tej grupy materiałów. Wynika to ze stosowanych metod syntezy, opierających się głównie na wysokotemperaturowym zagęszczaniu uformowanych wstępnie wyrobów. Porowatość w ,,surowym” materiale, przekracza zwykle 35 %–40 % i jest stopniowo usuwana podczas fizykochemicznego procesu spiekania [12, 13, 211]. Pory, są więc elementami mikrostruktury, które podobnie jak ziarna, mogą przyjmować różne kształty i rozmiary, zależne od metod stosowanych podczas całego procesu technologicznego. W niektórych rodzajach tworzyw ceramicznych, wykorzystywanych do produkcji izolacji cieplnych, akustycznych, filtrów czy katalizatorów, porowatość jest niezbędna do uzyskania oczekiwanych właściwości użytkowych [12, 50]. Jednak w przypadku wysokowytrzymałych, ceramicznych tworzywach konstrukcyjnych, obecność porów jest ograniczana w procesie technologicznym do wartości nieprzekraczających kilku procent objętościowych. Wynika to z opisywanego wcześniej negatywnego wpływu obecności porów na wytrzymałość, ale też na inne właściwości mechaniczne.
Aby uporządkować rozważania na temat wpływu porowatości na właściwości tworzyw ceramicznych, można skorzystać z podziału wprowadzonego przez Rice’a [211]. Wyróżnił on trzy zasadnicze grupy właściwości. Do pierwszej, można zatem zaliczyć te, które nie zależą od porowatości. Są to właściwości, wynikające jedynie z lokalnych oddziaływań na poziomie atomowym (zależą od rodzaju wiązania chemicznego) i nie są podatne na zaburzenia wprowadzane przez obecność porów. Należą do nich takie właściwości jak parametr sieciowy i, wynikająca z niego, objętość komórki elementarnej, temperatura topnienia, energia ablacji czy zdolność emisyjna.
Makroskopową właściwością związaną bezpośrednio z oddziaływaniami międzyatomowymi jest także rozszerzalność cieplna (por. rozdz. 1.2.4). W tym kontekście należałoby przyjąć, że nie powinna ona zależeć od porowatości. Jednak na rozszerzalność cieplną może mieć również wpływ obecność mikrospękań, będących skutkiem anizotropii albo różnicy w rozszerzalności cieplnej krystalitów. Takie mikrospękania, w trakcie ogrzewania i studzenia, mogą zamykać się lub otwierać, co powoduje powstawanie histerezy obserwowanej w trakcie pomiarów rozszerzalności cieplnej i wpływa na wartości liniowych współczynników \(\alpha\) [211–214].
Drugą grupę stanowią te właściwości, które zależą jedynie od udziału objętościowego porów \(V_{\text{p}}\), ale nie od ich specyfiki: kształtu, względnego ułożenia czy rozmieszczenia w objętości materiału. Do tej grupy zaliczyć można przykładowo gęstość, pojemność cieplną oraz względną przenikalność elektryczną [19, 211, 215]. Ich zależność od udziału objętościowego porów jest zgodna z regułą mieszanin: \[\label{eq:reg_miesz_porowatosc} X = (1 - V_{\text{p}}) X_0 + V_{\text{p}} X_1,\] w której \(X\) jest właściwością porowatego materiału, \(X_0\) właściwością fazy stałej (materiału niezawierającego porów (\(V_{\text{p}}= 0\))), a \(X_p\) właściwością fazy wypełniającej pory – zwykle \(X_p = 0\), ale dla współczynnika załamania fali w ośrodku, jak również względnej przenikalności elektrycznej \(X_p = 1\).
W trzeciej, największej i najbardziej złożonej grupie właściwości, mieszczą się te, które określone są poprzez strumień albo naprężenie przenoszone przez ciało. Zależą one zarówno od udziału objętościowego jak i specyfiki rozmieszczenia oraz kształtu porów. Dla właściwości charakteryzowanych strumieniem pola, opisujących przepływ prądu elektrycznego, ciepła czy płynu, istotny staje się dodatkowo rodzaj porowatości (otwarta, zamknięta), jej struktura, powierzchnia, przepuszczalność, jak również właściwości medium wypełniającego pory. Jest to więc zagadnienie złożone i stanowi przedmiot analiz dotyczących ceramiki wysoko porowatej stosowanej jako izolacje, filtry czy katalizatory [216–221]. Natomiast zjawiska wynikające z przenoszenia naprężeń w materiałach porowatych, odpowiadać będą za właściwości mechaniczne takie jak: sprężystość, wytrzymałość, odporność na pękanie oraz twardość.
Szeroki zakres wartości, które może przyjmować porowatość oraz wynikająca z tego różnorodność struktur, występujących w materiałach porowatych, sprawia, że do ich opisu stosowanych jest wiele modeli matematycznych (zob. tab. [1.2]). Często wykorzystywane są równania empiryczne, dostosowane do danego typu tworzyw, obecnej w nich porowatości i opisywanej właściwości. Najprostszym typem równań, służącym do określania zależności między wartościami modułów sprężystości a porowatością, są równania liniowe: \[\label{eq:por_liniowe} \frac{M}{M_0} = 1 - aV_{\text{p}},\] będące w istocie rozwinięciem reguły mieszanin \eqref{eq:reg_miesz_porowatosc}, w których \(M\) oznacza wybrany moduł sprężystości materiału porowatego (moduł Younga (\(E\)), sprężystości poprzecznej (\(\mathcal{G}\)), ściśliwości (\(\mathcal{K}\)), \(M_0\) jest odpowiednim modułem materiału niezawierającego porów, oraz \(a\) jest parametrem ustalanym na podstawie dopasowania [222, 223]. Równania te stosowane są dla porowatości nieprzekraczającej wartość 0.1. Przy wyższej porowatości, stosuje się zazwyczaj równania wykładnicze [224] w postaci: \[\label{eq:por_wykl} \frac{M}{M_0} = (1 - aV_{\text{p}})^n,\] w których wartości \(n\), podobnie jak \(a\) w równaniu \eqref{eq:por_liniowe}, zależą od rodzaju materiału i również ustalane są poprzez dopasowanie. Dla porowatości poniżej wartości krytycznej \(V_{\text{p}}^c\), przy której materiał traci spoistość (0.4 \(< V_{\text{p}}^c <\) 1), zależność modułów sprężystości od porowatości, może być również opisywana funkcją eksponencjalną [225, 226]: \[\label{eq:Spriggs1961} \frac{M}{M_0} = \mathop{\mathrm{e}}^{-b V_{\text{p}}},\] w której wartość parametru dopasowania \(b\), mieści się zwykle w granicach od 1 do 6 i jest zależna od kształtu i względnego ułożenia porów w materiale. Dokładne wartości parametru \(b\), ustalone dla wielu materiałów ceramicznych, można znaleźć w pracach Rice’a [145, 211], Anderssona [227] oraz w szeregu publikacji dotyczących materiałów porowatych. Należy też zauważyć, że analogiczne, eksponencjalne zależności stosowane są również do opisu wpływu porowatości na inne właściwości mechaniczne, takie jak wytrzymałość, odporność na pękanie i twardość [50, 53, 211, 228].
Wpływ porowatości na właściwości sprężyste jest również przedmiotem analiz mikromechanicznych (zob. rozdz. 3.2). Zagadnienie to stanowi szczególny przypadek homogenizacji, w której moduły sprężystości fazy wtrąconej – reprezentowanej przez pory, przyrównywane są do zera. Do opisu stosuje się tutaj modele oparte na koncepcji Eshelby’ego [229, 230], wykorzystujące granice Hashina–Shtrikmana [231, 232], związki podane przez Kustera i Toksöza [233] oraz Moriego i Tanakę [234]. Szczegółowy przegląd tego zagadnienia można znaleźć w wielu pracach dotyczących mikromechaniki ośrodków niejednorodnych [218, 235–237], a najczęściej wykorzystywane równania zawiera tabela [1.2].
Kolejną grupę równań opisujących wpływ porowatości na właściwości materiałów, stanowią równania wykorzystujące modele geometryczne. Należy do nich model oparty na koncepcji minimalnej powierzchni fazy stałej (MSA, ang. Minimum Solid Area) [238, 239]. W modelu tym zakłada się, że powierzchnia normalna do przyłożonych obciążeń, której pole zależy od kształtu i rozmieszczenia porów w materiale, będzie odpowiadała za przenoszenie zarówno strumienia pola jak i naprężeń. Dodatkowo przyjmuje się, że jej znormalizowana wartość (przypadająca na jednostkę powierzchni ciała) będzie, wraz ze zmianą porowatości, ewoluować tak, jak wartość względna rozważanej właściwości porowatego materiału [238–240]: \[\text{MSA} = \frac{M}{M_0}.\] Określenie zależności MSA od porowatości dla prostych kształtów porów i ich regularnego rozmieszczenia jest możliwe na podstawie podstawowych relacji geometrycznych. Dla bardziej skomplikowanych struktur stosuje się metody numeryczne [216, 219, 241].
Do metod opierających się na modelach geometrycznych należy zaliczyć również metody przybliżone, bazujące na rzeczywistych bądź syntetycznych mikrostrukturach21. Z uwagi na brak ograniczeń dotyczących kształtu, udziału objętościowego i rozmieszczenia porów w materiale, pozwalają one na analizę właściwości dla pełnego zakresu struktur [221, 242–244]. Uzyskiwane wyniki symulacji wykazują bardzo dobrą zgodność z wynikami pomiarów przeprowadzanych dla rzeczywistych tworzyw porowatych i dzięki temu mogą stanowić użyteczne narzędzie interpretacyjne [245–248].
Przedstawione tutaj krótkie zestawienie najważniejszych modeli i zależności, będących efektem kilkudziesięcioletniej historii badań nad porowatością, wskazuje, że nadal brakuje uniwersalnej teorii, która obejmowałaby cały zakres struktur i pozwalała na ilościowy opis zjawisk zachodzących w tworzywach porowatych. Wiele z przytoczonych równań, szczególnie empirycznych, dobrze opisuje wybrane rodzaje tworzyw w określonym zakresie porowatości, ale brakuje im zdolności predykcyjnej niezbędnej do szerszego wykorzystania ich w praktyce inżynierskiej. Z kolei, metody oparte na silnych podstawach teoretycznych – metody mikromechaniczne – pozwalają na szacowanie właściwości dla wybranych materiałów, jednak zakres niepewności uzyskiwanych wyników pozostaje wciąż zbyt duży [249]. Dokładny opis porowatości, podobnie zresztą jak i innych elementów mikrostruktury, musi zatem uwzględniać aspekt statystyczny, wynikający ze zróżnicowania morfologicznego i topologicznego materiałów. Dlatego wydaje się istotne, połączenie metod ilościowej analizy mikrostruktury, wykorzystującej trójwymiarowe modele rzeczywistych tworzyw, z metodami pozwalającymi na symulacje zachodzących w nich zjawisk. Integracja taka, pozwala na opis i analizę właściwości makroskopowych z uwzględnieniem oddziaływań lokalnych wynikających ze specyfiki materiału – w szczególności polikrystalicznego tworzywa ceramicznego.
Często wykorzystywana jest tutaj metoda elementów skończonych (MES).↩︎
W odróżnieniu od monokryształów, właściwości polikryształów, a w szczególności polikrystalicznych tworzyw ceramicznych, są ściśle związane z obecnością granic międzyziarnowych. Granice te, istotnie wpływają, a niekiedy wręcz decydują, o wielu makroskopowych właściwościach tego typu materiałów [37, 53, 250]. Są to zarówno właściwości opisujące transport ciepła, prądu elektrycznego, ale również właściwości mechaniczne, związane z przenoszeniem naprężeń.
Jak już wcześniej wspomniano, dzięki rozwojowi technik badawczych, w połączeniu z metodami symulacyjnymi, możliwe stało się lepsze poznanie budowy granic międzyziarnowych [251, 252]. Z uwagi na różną grubość (\(\sim\)0.2 nm–2 nm) oraz obecność domieszek, można zatem wyróżnić kilka typów granic, które posiadają specyficzne właściwości – swoją wewnętrzną strukturę – lecz nie mogą występować samodzielnie, bez faz otaczających [35, 40, 41, 253]. Takie międzyfazy, budujące granice międzyziarnowe, nazywane są niekiedy fazami naskórkowymi (ang. complexion). Do pierwszego typu zaliczane są więc granice czyste – niezawierające wytrąceń domieszek, które zwykle w procesie spiekania gromadzą się w obszarach międzyziarnowych. Kolejnymi typami są granice jedno-, dwu- i trójwarstwowe o grubości nieprzekraczającej 1 nm. W granicach tych obecne są niewielkie ilości domieszek, które stopniowo, wraz ze wzrostem ich stężenia, zwiększają zdefektowanie struktury. Granice o większej grubości – zbudowane z wielu warstw atomów – nazywane są granicami nanometrycznymi albo wielowarstwowymi. Posiadają one już istotnie zdefektowaną strukturę i zawierają fazę amorficzną. Ich grubość przekracza 1 nm, ale nie jest wprost związana z udziałem domieszek. Ostatni typ granic, to granice w których ulokowana jest faza ciekła w postaci filmu, którego grubość zależna jest bezpośrednio od udziału fazy amorficznej w materiale [35, 253].
Z uwagi na budowę, granice międzyziarnowe są więc elementami mikrostruktury, które z jednej strony mogą stanowić barierę na drodze przenoszonego strumienia czy rozprzestrzeniających się pęknięć, a z drugiej – tworzyć kanały przewodzenia, jak również uprzywilejowane ścieżki dekohezji (por. rozdz. 1.3.2 oraz 1.3.3). Wpływ obecności granic międzyziarnowych na właściwości materiału jest wiec złożony i dlatego do ich opisu, stosowane są modele fizyczne, specyficzne dla rozpatrywanego zjawiska. Tutaj jednak, dalsze rozważania ograniczone będą jedynie do najbardziej podstawowych właściwości tworzyw konstrukcyjnych – właściwości mechanicznych: wytrzymałości i odporności na pękanie. W zagadnieniach tych, granice międzyziarnowe traktowane są zazwyczaj w sposób klasyczny – jako obiekty dwuwymiarowe. Pomijana jest zatem ich grubość oraz wewnętrzna struktura. Takie uproszczenie stosowane jest w modelach analitycznych i pozwala na zwięzły opis zjawiska pękania.
W przypadku polikryształów ceramicznych, w których granice międzyziarnowe można zaklasyfikować do jednego z czterech pierwszych wymienionych typów (gdy ich grubość nie przekracza 1 nm), pękanie przebiegać może na dwa sposoby 22. Jeśli opór stawiany przez granice na rozprzestrzenianie się pęknięć \(R_{\text{gb}}\) jest niewielki, to dochodzi do ich dekohezji i rozwijająca się szczelina meandruje między ziarnami, biegnąc wzdłuż granic (pękanie międzyziarnowe). W przeciwnym wypadku, jeśli granice są mocne (\(R_{\text{gb}}\) jest wystarczająco duży, większy od oporu stawianego przez krystality \(R_{\text{g}}\)), to szczelina propaguje na wprost – przez ziarna (pękanie wskrośziarnowe). Najczęściej jednak obydwa scenariusze realizowane są równolegle i materiał ulega pękaniu zarówno wskroś-, jak i międzyziarnowemu. Odporność na pękanie granic międzyziarnowych wpływa zatem istotnie na mechanizmy występujące podczas niszczenia materiałów polikrystalicznych. Wartość energii pękania dla granic \(\gamma_{\text{gb}}\), jest zwykle zbliżona do połowy wartości energii pękania dla najsłabszych płaszczyzn łupliwości krystalitów [139]. Takie obniżenie wartości \(\gamma_{\text{gb}}\) wynika ze zdefektowania struktury na poziomie atomowym, którego stopień zależy od rodzaju oddziaływań międzyatomowych (wiązań chemicznych), udziału domieszek, ale również od czynników zewnętrznych (np. składu atmosfery, zawartości wilgoci) mogących wywoływać wzrost spękań sub-krytycznych [92, 139, 197, 254–256]. Osłabienie granic międzyziarnowych może być również spowodowane obecnością porów oraz mikrospękań będących efektem kumulacji naprężeń cieplnych [257–261] (zob. rozdz. 1.4).
Przyjmując, że szczelina propaguje w materiale wzdłuż ścieżki, dla której wartość szybkość uwalniania energii \(G\) jest najmniejsza, ale jednocześnie przekracza ona wartość krytyczną (spełniony jest warunek \eqref{eq:G_2gamma}, \(G > G_{\text{c}}= R = 2\gamma^{*}\)), o sposobie pękania – wskroś- czy międzyziarnowym – decydują więc wartości lokalnych, krytycznych szybkości uwalniania energii zarówno dla ziaren \(G_\text{g}\) jak i dla granic międzyziarnowych \(G_\text{gb}\). Wartości te są jednak uzależnione od względnej orientacji ziaren (płaszczyzn krystalograficznych) i granic oraz ich pozycji w odniesieniu do aktualnego kierunku propagacji szczeliny [92]. Dlatego zagadnienie to wymaga przyjęcia opisu stochastycznego, uwzględniającego zmienność wartości \(G_\text{g}\) oraz \(G_\text{gb}\).
Dwuwymiarowy model, uwzględniający losowe ułożenie ziaren względem propagującej szczeliny zaproponował Tatami i in. [262]. Oczekiwaną wartość udziału powierzchni powstałej na skutek pękania wskrośziarnowego \(\hat{f}\), powiązał on z rozmiarem ziarna \(d\), które znajduje się na drodze pęknięcia, co można zapisać równaniem: \[\label{eq:Tatami_f} \hat{f} = 1 - \frac{2y_c}{d},\] przy czym parametr \(y_c\) przyjmuje wartości od 0 do \(d/2\) i określa krytyczną odległość szczeliny \(y_c\) od górnej bądź dolnej powierzchni ziarna, przy której pękanie może dalej przebiegać międzyziarnowo – po tych powierzchniach. Odległość ta zależy od wartości krytycznych szybkości uwalniania energii charakteryzujących zarówno pękanie ziarna (\(G_{\text{Ic}}^{\text{g}}\)) jak i granicy (\(G_{\text{Ic}}^{\text{gb}}\)) i dana jest wyrażeniem [262]: \[\label{eq:Takami_yc} y_c = \frac{-q+\sqrt{q^2 + 2\left( \frac{G_{\text{Ic}}^{\text{g}}}{G_{\text{Ic}}^{\text{gb}}} - 1 \right)pd}}{p}.\] Parametry \(p\) i \(q\) są stałymi, które Tatami [262] określił na podstawie dopasowania równania do danych empirycznych dla polikrystalicznego \(\text{AlN}\). Równanie to pozwala na obliczenie \(y_c\) dla ziaren, których rozmiary są większe od minimalnej wartości \(d^{\ast}\), przy której pojawia się pękanie wskrośziarnowe. Poniżej tej wartości pękanie będzie zachodzić wyłącznie międzyziarnowo, zatem \(y_c = d/2\) i tym samym wartość \(\hat{f} = 1\) \eqref{eq:Tatami_f}. Natomiast wartość \(d^{\ast}\) można obliczyć na podstawie równania [262]: \[\label{eq:Tatami_d} d^{\ast} = \frac{8\left( \frac{G_{\text{Ic}}^{\text{g}}}{G_{\text{Ic}}^{\text{gb}}} - 1 \right) - 4q}{p}.\]
Pomimo dużych uproszczeń dotyczących geometrii ziaren23, które przyjęte zostały w przedstawionym modelu, pozwala on na uporządkowanie i analizę istotnych czynników decydujących o pękaniu polikryształów. Przede wszystkim na sposób, w jaki rozprzestrzeniają się pęknięcia, decydujący wpływ mają zarówno wartości odporności na pękanie ziaren, jak i granic międzyziarnowych. W modelu, do opisu tych właściwości, zostały wykorzystane \(G_{\text{Ic}}^{\text{g}}\) i \(G_{\text{Ic}}^{\text{gb}}\), ale w odniesieniu do konkretnego materiału można opisać je przy pomocy odpowiednich energii pękania krystalitów \(\gamma_{\text{g}}\) i granic \(\gamma_{\text{gb}}\). Istotna jest zatem wartość względna, a nie tylko bezwzględne wartości wyznaczone niezależnie dla ziaren i granic. Ma to szczególnie znaczenie w przypadku, gdy modyfikacji podlega stężenie domieszek, wydzielających się w granicach międzyziarnowych. Obecność takich domieszek może więc powodować obniżenie wartości \(\gamma_{\text{gb}}\) przy niezmienionej wartości \(\gamma_{\text{g}}\), co w efekcie może doprowadzić do zmiany charakteru pękania – ze wskroś- na międzyziarnowe, a tym samym na wytrzymałość i odporność na pękanie.
Kolejnym elementem ujętym w przedstawionym modelu jest rozmiar ziarna. Obserwacje przeprowadzone dla wielu różnych polikryształów ceramicznych, potwierdzają wzrost udziału pękania wskrośziarnowego wraz ze wzrostem rozmiaru krystalitów [9, 15, 50, 92, 139, 263]. Zjawisko to jest szczególnie widoczne w materiałach zawierających ziarna o nieizometrycznych kształtach. Jednak czynnik ten, staje się istotny dopiero po przekroczeniu pewnego minimalnego rozmiaru ziaren, który w opisanym modelu został oznaczony jako \(d^{\ast}\). Poniżej tej wartości wyraźnie dominuje pękanie międzyziarnowe, a dekohezja krystalitów występuje sporadycznie i pojawia się jedynie w pobliżu krawędzi ziaren.
Rozpoznanie mechanizmu dominującego w trakcie pękania polikryształów ceramicznych może być jednak użyteczne nie tylko w aspekcie poznawczym, ale przede wszystkim może posłużyć do świadomej modyfikacji właściwości tworzywa [251, 264]. Polikryształy, w których zarówno granice, jak i ziarna, charakteryzują się wysokimi wartościami energii pękania (\(\gamma_{\text{gb}}\), \(\gamma_{\text{g}}\)), zaliczane są zwykle do grupy materiałów o wysokiej wytrzymałości. Dominujący w nich wskrośziarnowy mechanizm dekohezji, sprzyja jednak katastrofalnemu pękaniu [37, 264, 265]. Wprowadzenie zatem, niewielkiej ilości dodatków obniżających energię pękania granic międzyziarnowych, może zwiększyć udział pękania międzyziarnowego i tym samym uruchomić szereg mechanizmów zwiększających odporność na pękanie. Opisywane wcześniej mostkowanie, wyciąganie i blokowanie ziaren, odchylanie oraz klinowanie pęknięć (p. 1.3.3), może stać się bowiem efektywne, dopiero w przypadku ,,osłabienia” kontaktów międzyziarnowych [266, 267]. Modyfikacje takie, prowadzą jednak do obniżenia ogólnej wytrzymałości tworzywa. Dlatego niezbędna jest analiza zmian rozpatrywanych właściwości i ewentualna dalsza optymalizacja składu oraz mikrostruktury badanego materiału.
Czynniki, które ujęte zostały w modelu zaproponowanym przez Tatami i in. [262], nie wystarczają jednak do pełnego opisu pękania polikryształów ceramicznych. Jak już wspomniano, istotnym parametrem wpływającym na energię pękania krystalitów jest ich orientacja względem propagującej szczeliny. Wartości \(\gamma_{\text{g}}\) zmieniają się dla różnych płaszczyzn krystalograficznych (płaszczyzn łupliwości), a tym samym – zależnie od kąta odchylenia (\(\theta\)) i skręcenia (\(\phi\)) tych płaszczyzn względem płaszczyzny pęknięcia – zmieniają się również wartości \(G_{\text{Ic}}^{\text{g}}\). Ich zmienność można wyrazić z wykorzystaniem funkcji kątowych Cotterella i Rice’a [190], analogicznie do lokalnych współczynników intensywności naprężeń \eqref{eq:FaberEvans_kt}, opisanych wcześniej dla mechanizmu odchylania pęknięć [92].
Kolejnym istotnym czynnikiem wpływającym na wytrzymałość granic międzyziarnowych, i w efekcie na rodzaj pękania, jest obecność mikrospękań [19, 44, 50, 144, 175, 212]. Są one indukowane naprężeniami cieplnymi, powstającymi podczas chłodzenia materiału. Naprężenia te, wynikające z różnic pomiędzy liniowymi współczynnikami rozszerzalności cieplnej stykających się ze sobą ziaren, są obecne zarówno w materiałach wielofazowych, jak i jednofazowych, w których występuje anizotropia rozszerzalności cieplnej krystalitów [201, 257, 258, 268] (zob. rozdz. 1.4). Pojawienie się zatem mikrospękań w granicach międzyziarnowych, uwarunkowane jest zarówno właściwościami samej granicy, jak również właściwościami termomechanicznymi krystalitów. Na wartość naprężeń cieplnych, skumulowanych w granicy międzyziarnowej, ma dodatkowo wpływ kształt, rozmiar i orientacja sąsiadujących krystalitów. Należy też zauważyć, że mikrospękania mogą również tworzyć się w strefie poprzedzającej front szczeliny – strefie procesowej (ang. process zone). Zjawisko to wynika bezpośrednio z rozkładu pola naprężeń \(\sigma_{ij}\) w pobliżu wierzchołka szczeliny \eqref{eq:Irwin_pole}.
Oszacowanie minimalnej wartość średnicy ziarna \(D_{\text{min}}\), powyżej której w polikrysztale mogą tworzyć się mikrospękania, zaproponowali Cleveland i Bradt [269]: \[\label{eq:Cleveland-Bradt} D_{\text{min}} = \frac{a\,\gamma_{\text{gb}}}{E\, {\varepsilon^{\text{T}}}^2}.\] Właściwości granicy międzyziarnowej, zostały wyrażone tutaj poprzez energię pękania \(\gamma_{\text{gb}}\), a właściwości ziaren, jako moduł Younga \(E\) i odkształcenie cieplne \(\varepsilon^{\text{T}}= \Delta\alpha_{\text{max}} \Delta T\), wywołane chłodzeniem o \(\Delta T\) i maksymalną różnicą liniowych współczynników rozszerzalności cieplnej \(\Delta\alpha_{\text{max}}\). Podstawiając do powyższego równania wartość współczynnika geometrycznego \(a =\)14.4, można określić minimalną średnicę, przy której w strefie procesowej pojawiają się mikrospękania. Wartość współczynnika \(a\) została ustalona przez Clevelanda i Bradta [269] dla ziaren o kształcie dwunastościanu. Natomiast dla ziaren elipsoidalnych, wartość współczynnika \(a =\)17 wyznaczyli Evans i Faber [270]. Zauważyli oni również, że średnica ziarna obliczona dla wartości \(a =\)40, określać będzie granicę, powyżej której dochodzić będzie do spontanicznego tworzenia się mikrospękań w polikrysztale – nawet poza strefą procesową. Inaczej mówiąc, średnica ta (\(D_{\text{c}}\)) charakteryzuje materiał, w którym mikrospękania pojawiają w trakcie studzenia, jedynie na skutek działania naprężeń cieplnych 24. Oszacowane w ten sposób średnice ziaren, są więc użytecznymi parametrami ilościowymi, łączącymi najważniejsze czynniki, które mogą wywoływać powstawanie mikrospękań w obszarze kontaktu pomiędzy ziarnami.
Wpływ naprężeń cieplnych, nie ogranicza się jednak tylko do oddziaływań w samej granicy – co prawda wartości tych naprężeń są tam największe [178, 271–274], ale również wewnątrz ziaren mogą one wpływać na lokalne wartości szybkości uwalniania energii (\(G\)) i tym samym modyfikować ścieżki dekohezji. Dlatego coraz częściej, zjawisko pękania polikryształów analizowane jest metodami numerycznymi w oparciu o strukturę atomową sieci krystalicznej albo – w skalach większych (mikro- i mezoskali) – na podstawie rzeczywistych bądź syntetycznych modeli mikrostruktury. W metodach tych, właściwości ziaren i granic międzyziarnowych, a w szczególności ich spoistość, analizowane są bezpośrednio – z uwzględnieniem oddziaływań na poziomie atomowym – albo pośrednio przy pomocy przybliżeń (modeli materiałowych), uwzględniających tego typu oddziaływania. Pozwala to na szczegółowy opis zachowania polikryształu, lecz okupione jest dużo większą złożonością modeli matematycznych.
Koncepcja oparta na oddziaływaniach międzyatomowych, decydujących o kohezji ciała, jest rozwijana równolegle do mechaniki ośrodków ciągłych już od lat 40. ubiegłego stulecia. Została ona wykorzystana przez Orowana [63], a później przez Gilmana [275] do opisu, wspomnianej już wcześniej (rozdz. 1.2.2), wytrzymałości kohezyjnej (teoretycznej). Orowan przybliżył wewnętrzne oddziaływania pomiędzy atomami ulokowanymi w pobliżu rozwieranej szczeliny funkcją, określającą zależność między naprężeniem kohezyjnym a przemieszczeniem [63]: \[\label{eq:Orowan_F} \sigma(u) = \sigma_c \sin \left( \frac{2 \pi u}{\lambda} \right)\!,\] przy czym \(\sigma_c\) jest wytrzymałością kohezyjną (\(\sigma_c = \sigma_t\)). Zależność ta opisuje zatem oddziaływanie między atomami w zakresie przemieszczeń ograniczonych parametrem \(\lambda\) (\(0 \leqslant 2u \leqslant \lambda\)). Parametr ten, jest więc odległością, przy której dochodzi do zerwania wiązania między parą atomów – gdy \(2u > \lambda\), to \(\sigma(u) = 0\) (rys. 1.10). Powierzchnia pod krzywą \(\sigma(u)\), określa więc pracę (odniesioną do jednostkowej powierzchni) jaka musi zostać wykonana na rozdzielenie sąsiadujących atomów: \[\label{eq:OrowanGamma} W = \int\limits_{0}^{\lambda} \sigma(u)\mathop{}\!\mathrm{d}(2u) = \frac{2\lambda}{\pi}\sigma_c = 2\gamma.\] Przy założeniu, że parametr \(\lambda\) jest w przybliżeniu równy odległości równowagowej \(a_0\), a moduł Yonuga można wyrazić poprzez styczną do krzywej \(\sigma(u)\) w punkcie \(a_0\) (\(E = \pi a_0/\lambda\, \sigma_c\)), równanie to można przekształcić do postaci przedstawionej wcześniej (zob. rozdz. 1.2.2), definiującej wytrzymałość teoretyczną \(\sigma_c = \sigma_{\text{t}}= \sqrt{E\gamma/a_0}\) \eqref{eq:sigma_max} [92, 276].
W porównaniu do fenomenologicznego opisu pękania przedstawionego przez Griffitha, przybliżenie Gilmana, opierające się na kohezji wynikającej z oddziaływań na poziomie atomowym, stanowiło krok w kierunku fundamentalnego ujęcia problemu wytrzymałości. Jednak zarówno wartość \(\lambda\), jak również kształt zależności \(\sigma(u)\) są ściśle związane z rodzajem oddziaływań występujących między rozdzielanymi atomami (wiązań chemicznych), dlatego aktualnie do analizy oddziaływań występujących podczas dekohezji w skali atomowej stosowane są metody ab initio oraz MD [121, 129, 278–289]. Zastosowanie tych metod pozwala na szczegółową analizę zjawisk zachodzących w pobliżu wierzchołka szczeliny, uwzględniającą również reakcje chemiczne pomiędzy rozpatrywanym materiałem a czynnikami środowiskowymi (hydroliza, korozja) [290–293]. Z drugiej strony, duży koszt obliczeniowy, związany z koniecznością symulacji oddziaływań pomiędzy wieloma atomami (>e6), ogranicza możliwość analizowania złożonych struktur polikrystalicznych. Pomijając przybliżenia wynikające ze specyfiki metod, stosowane uproszczenia zwykle dotyczą geometrii analizowanego układu. Najczęściej symulacje prowadzone są więc dla struktur o grubości zredukowanej do wymiarów komórki elementarnej, a niekiedy dla dwuwymiarowej geometrii, przy jednoczesnym ograniczeniu rozmiaru modelu do niewielkiej liczby ziaren. Pomimo takich uproszczeń, symulacje te wymagają stosowania wysokowydajnej infrastruktury obliczeniowej (HPC, ang. High Performance Computing) [288, 292, 293].
Dlatego równolegle do metod opartych na zasadach pierwszych, rozwijane są metody umożliwiające symulacje w większych skalach. Należy jednak podkreślić, że wyniki analiz prowadzonych w skali atomowej są niezwykle cenne i coraz częściej stanowią dane wejściowe dla modeli numerycznych opisujących zachowanie struktur polikrystalicznych. Takie podejście, nazywane modelowaniem wieloskalowym, polegające na łączeniu skal (nano-mikro-mezo-makro), stanowi w ostatnich latach szybko rozwijający się kierunek badań w obliczeniowej inżynierii materiałowej (zob. rozdz. 3.3.2). Właściwości określone dla jednej skali zostają poddane homogenizacji i stanowią parametr wykorzystywany do modelowania kolejnej, większej skali [281, 286, 294–299].
Jedna z takich koncepcji, często wykorzystywana do opisu zjawiska pękania polikryształów, opiera się na przybliżaniu oddziaływań występujących w pobliżu wierzchołka szczeliny, oddziaływaniami sprężysto-plastycznymi. Została ona wprowadzona przez Dugdale’a [300] i Barenblatta [301] i później zaimplementowana w MES przez Needlemana [302]. Opiera się ona na założeniu, że przed frontem pęknięcia, po osiągnięciu maksymalnych naprężeń, tworzy się strefa nieodwracalnych deformacji nazywana strefą kohezyjną (ang. cohesive zone). W obszarze tym, dochodzi do stopniowej degradacji materiału, której towarzyszy lokalny spadek spoistości. W szerokim ujęciu, może to obejmować wszystkie procesy towarzyszące rozwojowi pęknięcia, takie jak przykładowo: mostkowanie, klinowanie i wyciąganie, spowodowane zarówno przez izometryczne ziarna jak i krótkie bądź długie włókna, ale również powstawanie mikrospękań, przemiany fazowe i inne zjawiska prowadzące do dyssypacji energii. Jednak w kontekście pękania wskroś- i międzyziarnowego, najistotniejsze jest osłabienie wynikające ze stopniowego zaniku oddziaływań międzyatomowych – zrywania wiązań chemicznych, do którego dochodzi wskutek przemieszczenia atomów wywołanego odkształceniem (rys. 1.11).
Kluczowym parametrem opisującym strefę kohezyjną jest funkcja określająca zależność pomiędzy naprężeniem kohezyjnym \(\sigma_\text{koh}\), pojawiającym się w rozdzielanych obszarach a względnym przemieszczeniem – separacją \(\delta\) wywołującą to naprężenie (ang. traction-separation law). W istocie, funkcja ta opisuje więc rozpatrywaną wcześniej zależność \(\sigma(u)\), umożliwia zatem określenie pracy niezbędnej do powiększenia szczeliny, która jest równoważna energii pękania strefy kohezyjnej (rys. 1.10). Można to wyrazić w sposób analogiczny do równania \eqref{eq:OrowanGamma}, jako: \[\label{eq:G_coh} W = \int\limits_{0}^{\delta_f} \sigma_{\text{koh}}(\delta)\mathop{}\!\mathrm{d}\delta = G_{\text{koh}}.\] Jeśli zatem szybkość uwalniania energii w strefie kohezyjnej \(G \geqslant G_{\text{koh}} = G_{\text{c}}\), to przekroczony zostanie opór materiału i dojdzie do rozwarstwienia.
Związki konstytutywne, w modelu strefy kohezyjnej (CZM, ang. Cohesive Zone Model), ustalane są najczęściej na podstawie funkcji określającej zmiany energii potencjalnej względem przemieszczenia \eqref{eq:Upot_u} [277, 303, 304]. Uzyskane w ten sposób zależności \(\sigma_{\text{koh}}(\delta)\), opisywane są krzywymi eksponencjalnymi [305–307], trapezoidalnymi [308], albo wielomianami [302, 309], określonymi poprzez stałe – parametry dopasowania. W zależności od zastosowanego rozwiązania, parametrami tymi mogą być zarówno wartości separacji \(\delta\), wyznaczające charakterystyczne etapy dekohezji (rys. 1.11), jak i odpowiadające im wartości \(\sigma_{\text{koh}}\). Niekiedy w roli parametrów modelu stosuje się również wartości szybkości rozpraszania energii \(G_{\text{koh}}\), wymaganej do separacji dla wybranych typów obciążenia [310]. Ponieważ wymienione metody opisu strefy kohezyjnej opierają się na fizycznych związkach określających oddziaływania występujące przed frontem szczeliny, to wartości odpowiednich parametrów modelu dobierane są na podstawie bezpośrednich pomiarów albo symulacji numerycznych, przeprowadzonych dla rozpatrywanych materiałów [281, 311–314].
Stosując trapezoidalne dopasowanie zależności \(\sigma_{\text{koh}}(\delta)\) [308], model strefy kohezyjnej dla pierwszego typu obciążenia można opisać jako [19]: \[\label{eq:CZM_trapez} \sigma_{\text{koh}}^n = \begin{cases} E_e\frac{\delta}{\delta_0}, & \delta < \delta_1\\ \sigma_c^n, & \delta_1 \leqslant \delta \leqslant \delta_2\\ \sigma_c^n - E_p \frac{\delta - \delta_2}{\delta_0}, & \delta > \delta_2\\ 0, & \delta > \delta_{\!f} \end{cases}\] gdzie: \(E_e\) oraz \(E_p\) są modułami sztywności opisującymi właściwości elementu kohezyjnego, parametr \(\delta_0\) odpowiada równowagowej odległości międzyatomowej (\(\delta_0 = a_0\), jednak zwykle, jest on traktowany jako parametr numeryczny, przyjmujący bardzo małe wartości), a \(\delta_1\) i \(\delta_2\) są granicznymi wartościami separacji, pomiędzy którymi dekohezja następuje przy stałej szybkości uwalniania energii i naprężenie kohezyjne osiąga maksimum. W modelach opierających się na dopasowaniu bilinearnym albo wykorzystujących krzywe eksponencjalne czy wielomiany, wartości \(\delta_1\) i \(\delta_2\) są zastępowane pojedynczą wartością separacji \(\delta_c\), przy której \(\sigma_{\text{koh}} = \sigma_c\). Z kolei \(\delta_{\!f}\) określa maksymalną odległość oddziaływań kohezyjnych. Rozpatrując złożony stan obciążeń szczeliny, analogiczne zależności formułowane są również dla naprężeń ścinających (\(\sigma_{\text{koh}}^t\) i \(\sigma_{\text{koh}}^s\)).
Najbardziej intuicyjne wykorzystanie CZM, sprowadza się oczywiście do analizy dekohezji zachodzącej w granicach międzyziarnowych. Warto zauważyć, że analiza taka nie wymaga wprowadzenia do modelu pozycji i rozmiarów szczeliny a priori – do inicjacji mikropęknięć dochodzić może bowiem, dopiero na skutek przyłożonych obciążeń, w obszarach, w których kształt i orientacja krystalitów, doprowadzi do lokalnej kumulacji naprężeń (w których wartość \(G > G_{\text{koh}}\)). Implementacja CZM w modelach MES, polega na opisie właściwości krystalitów przy pomocy standardowych elementów termosprężystych25, pomiędzy którymi, umieszczane są elementy kohezyjne, zapewniające możliwość analizy pękania granic międzyziarnowych [313, 315–318]. Rozwinięciem tej koncepcji jest wprowadzenie elementów kohezyjnych również do wnętrza krystalitów. Pozwala to na symulację pękania wskrośziarnowego. Elementy takie mogą być rozmieszczone wzdłuż wybranych płaszczyzn odpowiadających uprzywilejowanym płaszczyznom łupliwości, albo pomiędzy elementami siatki, którymi opisane są krystality [319–323].
Wykorzystując model strefy kohezyjnej, możliwe jest więc analizowanie zarówno pękania wskroś-, jak i międzyziarnowego. Z uwagi na wysoki koszt obliczeniowy, wynikający z nieliniowego charakteru opisywanego zjawiska, oraz dużej liczby elementów niezbędnych do dyskretyzacji modelu, analizy ograniczone są często do przypadków dwuwymiarowych. W symulacjach takich, wykorzystywane są modele geometryczne oparte na rzeczywistych obrazach mikrostruktury, a także uproszczonym kształcie ziaren – pozwalające na systematyczną analizę wpływu wybranych cech mikrostruktury na zjawisko pękania polikryształów [208, 324–326]. W ostatnim dziesięcioleciu, na skutek wzrostu dostępności HPC, symulacje prowadzone są również w oparciu o trójwymiarowe, realistyczne modele mikrostruktury, zrekonstruowane na podstawie danych doświadczalnych, albo wygenerowane metodami symulacyjnymi26 [299, 313, 323, 327]. W literaturze, dotyczącej modelowania właściwości tworzyw ceramicznych z wykorzystaniem CZM, obszerną grupę stanowią prace, w których analizowanym materiałem jest polikrystaliczny tlenek glinu. Z uwagi na stosunkowo niski koszt przygotowania próbek oraz dobrze poznanym i udokumentowanym właściwościom, stanowi on materiał referencyjny, służący do walidacji uzyskiwanych wyników symulacji [207, 313, 316, 319, 324, 328–331]. Wiele prac poświęconych jest również innym, jedno- i wielofazowym materiałom ceramicznym takim jak: \(\text{SiC}\), \(\text{B}_{\text{4}}\text{C}\), \(\text{TiB}_{\text{2}}\), \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), \(\text{ZrO}_{\text{2}}\) [325, 327, 328, 332, 333] oraz kompozytom ziarnistym [318, 323, 328, 334–336]. Symulacje takie stanową więc uzupełnienie metod doświadczalnych – badań fraktograficznych, wytrzymałościowych – wykorzystywanych tradycyjnie do opisu i analizy pękania polikryształów. Pozwalają również na rozpatrywanie wybranych efektów wynikających ze specyficznych cech mikrostruktury, właściwości faz składowych oraz granic międzyziarnowych, które byłyby trudne do analizy w rzeczywistych materiałach.
Zakładając, że materiał zachowuje się zgodnie z modelem ciała krucho-sprężystego. Dla polikryształów ceramicznych, takie założenie spełnione jest w temperaturze nieprzekraczającej 0.7–0.8 wartości temperatury topnienia.↩︎
Tatami i in. [262] rozważali przypadek dwuwymiarowy i przyjęli dodatkowo, że ziarna mają kształt kwadratu o długości boku \(d\).↩︎
Zagadnienia związane z wpływem resztkowych naprężeń cieplnych na właściwości polikrystalicznych tworzyw ceramicznych zostaną szerzej omówione w p. 1.4.4.↩︎
Podczas analizy zjawiska pękania tworzyw ceramicznych, zwykle stosuje się sprężysto-kruchy model materiałowy. Uwzględnienie zjawisk cieplnych, pozwala na rozszerzenie analizy o resztkowe naprężenia cieplne.↩︎
Metody rekonstrukcji mikrostruktury zostaną szerzej omówione w rozdziale 2.↩︎
Przedstawiony w poprzednich punktach opis właściwości i ich związków z wybranymi cechami mikrostruktury polikrystalicznych materiałów ceramicznych, wskazuje, że resztkowe naprężenia cieplne (RTS, ang. Residual Thermal Stresses), mogą istotnie wpłynąć na wytrzymałość i odporność na kruche pękanie rozpatrywanych tworzyw. Dodatkowo, obecność RTS jest immanentną cechą tej grupy materiałów. Wynika to zarówno ze specyfiki metod, którymi są one otrzymywane, jak i z ich budowy wewnętrznej. Naprężenia cieplne powstają w trakcie chłodzenia, po wysokotemperaturowym procesie spiekania, i są wywołane odkształceniem cieplnym krystalitów. Z uwagi na różnicę, albo anizotropię, w rozszerzalności cieplnej sąsiadujących ze sobą ziaren, odkształcenia te są niejednorodne i prowadzą do wzrostu wartości naprężeń. Zjawisko to jest szczególnie widoczne w tworzywach kompozytowych, w których fazy posiadają różną rozszerzalność cieplną i przez to wartości RTS mogą osiągać tutaj rząd GPa [178, 200, 337–339]. W materiałach jednofazowych niedopasowanie odkształceń cieplnych jest zwykle mniejsze i wynika z anizotropii rozszerzalności cieplnej krystalitów, zależnej od układu krystalograficznego. Wartości RTS są w tych materiałach rzędu dziesiątek albo setek MPa [200, 274, 340, 341]. Dla układu regularnego, w którym osiowe współczynniki rozszerzalności cieplnej są sobie równe, niejednorodność odkształceń, a tym samym wartości naprężeń cieplnych są najmniejsze i wynikają jedynie z anizotropii właściwości sprężystych. Dlatego obecność naprężeń cieplnych w materiałach o takiej strukturze, jest często pomijana w rozważaniach dotyczących właściwości mechanicznych [139].
Samo zjawisko, wynikające z narastania naprężeń cieplnych w procesie technologicznym, w którym występuje etap chłodzenia, nie jest oczywiście specyficzne tylko dla tworzyw ceramicznych. Jednak w tworzywach tych, różnica pomiędzy temperaturą syntezy a temperaturą użytkowania jest szczególnie duża (dla ceramiki węglikowej może przekraczać 2000 °C [1], co w połączeniu z ograniczoną możliwością relaksacji, prowadzi do kumulacji naprężeń cieplnych. Relaksacja naprężeń, zachodzi głównie w początkowym etapie chłodzenia, w temperaturze niewiele niższej od temperatury procesu spiekania. Przebiega ona wtedy poprzez pełzanie i odkształcenia plastyczne. Mechanizmy te, w wysokiej temperaturze, są na tyle wydajne, że w chłodzonym, z kontrolowaną szybkością, tworzywie, nie występują naprężenia cieplne. Jednak poniżej pewnej wartości temperatury \(T_{\text{sf}}\) (ang. stress free temperature), ich skuteczność spada i dalsza relaksacja może odbywać się już tylko poprzez dekohezję materiału – z wytworzeniem mikrospękań obniżających wytrzymałość [139, 342, 343] (zob. rozdz. 1.3.5). Wartość temperatury, poniżej której w tworzywie rozpoczyna się proces kumulacji naprężeń cieplnych, oznacza więc zarówno istotne ograniczenie efektywności procesów dyfuzyjnych, zachodzących podczas spiekania, jak i poślizgu dyslokacji, odpowiadającego za mikroplastyczność krystalitów. Określa ona również zmianę właściwości granic międzyziarnowych, w których ustaje płynięcie lepkościowe fazy amorficznej. Temperatura ta, wyznacza więc przejście materiału do stanu, w którym jego właściwości można opisywać modelem ciała sprężysto-kruchego. Dokładna wartość temperatury \(T_{\text{sf}}\) jest trudna do analitycznego określenia, szczególnie, że zależy ona również od szybkości chłodzenia i mikrostruktury analizowanego tworzywa. Najczęściej, dla jednofazowych polikryształów ceramicznych, przyjmuje się, że zawiera się ona w przedziale 0.7–0.8 wartości temperatury topnienia. W przypadku materiałów wielofazowych, reguła ta opiera się na najniżej topliwej fazie składowej, a w przypadku obecności w granicach międzyziarnowych fazy amorficznej, zwykle przyjmuje się, że \(T_{\text{sf}}\) jest równa temperaturze topnienia tej fazy [344]. Bardziej precyzyjne wartości \(T_{\text{sf}}\) uzyskuje się metodami doświadczalnymi – zwykle na podstawie pomiarów dylatometrycznych, oraz metodami strukturalnymi (XRD, ND) [343, 345–347].
Naprężenia cieplne nie są jedynym składnikiem naprężeń resztkowych. W szerszym ujęciu, naprężenia resztkowe (własne, RS, ang. Residual Stresses) są definiowane jako naprężenia, które pozostają w materiale po etapie produkcji i obróbki, przy jednoczesnym braku sił zewnętrznych i gradientów temperatury [349, 350]. Należy więc przyjąć, że praktycznie wszystkie procesy produkcyjne, wprowadzają naprężenia resztkowe do otrzymywanych wyrobów. Również ekstremalne obciążenie eksploatacyjne mogą zmienić stan naprężeń resztkowych w pracującym elemencie urządzenia (rys. 1.12). Ich wpływ może być zarówno korzystny jak i szkodliwy, w zależności od znaku, wielkości i rozkładu w elemencie konstrukcyjnym. Bezpośrednim źródłem naprężeń resztkowych, mogą być niedopasowania wymiarowe pomiędzy częściami w obrębie danego modułu urządzenia, ale również niedopasowania wynikające z różnic we właściwościach cieplnych, sprężystych, plastycznych, a nawet chemicznych, pomiędzy różnymi obszarami w obrębie jednej części [342, 349, 351–353]. Są one generowane podczas spawania, kiedy w pobliżu łączonych powierzchni, w strefie procesowej, pojawiają się duże gradienty temperatury – najpierw podczas ogrzewania, a potem chłodzenia [342, 352, 354–356]. W przypadku materiałów kruchych, odpowiednikiem tego zjawiska, może być wstrząs cieplny, wywołany gwałtowną zmianą temperatury otoczenia. Powstający w materiale gradient temperatury może wtedy doprowadzić do jego spękania, a niekiedy do całkowitego zniszczenia elementu konstrukcji [12, 353]. Naprężenia resztkowe powstają również podczas niejednorodnej deformacji plastycznej, która jest wykorzystywana zarówno podczas obróbki powierzchni (polerowanie, kulkowanie), jak i całej objętości materiału (walcowanie, kucie, wyciskanie, gięcie, ciągnienie, tłoczenie) [342, 352, 357]. Zastosowanie pokryć, w postaci cienkich warstw oraz powłok, w celu ochrony przed korozją, zużyciem ciernym czy poprawą biokompatybilności, również wprowadza naprężenia resztkowe. Mogą one w trakcie eksploatacji, prowadzić do stopniowego pogarszania parametrów użytkowych – a nawet pęknięć i odprysków naniesionej warstwy [342, 349, 351, 353, 358].
Wymienione do tej pory przypadki, w których źródłem naprężeń resztkowych były niedopasowania geometryczne, mechaniczne i cieplne, mogą dotyczyć całych elementów konstrukcji, bądź rozległych obszarów ulokowanych na ich powierzchni lub we wnętrzu. Występujące tam naprężenia resztkowe, klasyfikowane są często jako makro- i mezoskopowe. Oznacza to, że fluktuacje wartości tych naprężeń, ustalają się w przestrzeni o wymiarach od setek mikrometrów nawet do metrów (rys. 1.13). Warunek równowagi panującej wewnątrz ciała, można zatem wyrazić równaniem [342, 343]: \[\label{eq:residual_stress_equil} \int\limits_{A} \sigma_{n}^{\text{I}} \mathop{}\!\mathrm{d}A = \int\limits_{V} \sigma_{ij}^{\text{I}} \mathop{}\!\mathrm{d}V = 0,\] w którym \(\sigma_{n}^{\text{I}}\) jest składową normalną naprężeń resztkowych do wybranej powierzchni \(A\), natomiast \(\sigma_{ij}^{\text{I}}\) dowolną składową tensora naprężeń resztkowych w ciele o objętości \(V\). Tak zapisany warunek równowagi, oznacza więc, że rozważając odpowiednio dużą powierzchnię przekroju \(A\) lub objętość \(V\), które obejmują cały element konstrukcji (makroskopową próbkę), bądź fragment o rozmiarach znacznie przekraczających wymiary ziaren (próbkę w skali mezo), naprężenia resztkowe znoszą się i ich średnia, wyznaczona dla powierzchni bądź objętości, przyjmuje wartość zero (\(\langle\sigma\rangle^{\text{I}} = 0\)).
Obecność naprężeń resztkowych o tak dużym zasięgu, często w literaturze określanych jako naprężenia typu I 27, musi zostać uwzględniona podczas prac inżynierskich, związanych z projektowaniem konstrukcji urządzeń. W zagadnieniach dotyczących właściwości samych materiałów, istotne stają się natomiast naprężenia, których lokalne fluktuacje ustalają się w skali mikrometrycznej – odpowiadającej wymiarom ziaren (rys. 1.13). W takiej skali, warunek równowagi \eqref{eq:residual_stress_equil}, dla materiału dwufazowego, można zapisać w postaci równania [360]: \[\label{eq:residual_micro_equil} \int\limits_{A_\alpha} \sigma_{n}^{\text{II}} \mathop{}\!\mathrm{d}A + \int\limits_{A_\beta} \sigma_{n}^{\text{II}} \mathop{}\!\mathrm{d}A = f_\alpha \langle \sigma_\alpha \rangle^{\text{II}} + \left(1- f_\alpha \right) \langle \sigma_\beta \rangle^{\text{II}}= 0,\] przy czym, \(A_\alpha\) i \(A_\beta\) odpowiadają powierzchniom kolejnych faz na przekroju \(A\) (\(A = A_\alpha + A_\beta\)), a ich udział (powierzchniowy) określony jest odpowiednio, współczynnikiem \(f_\alpha\) oraz \(\left( 1 - f_\alpha \right)\). Zatem naprężenia resztkowe w mikroskali \(\sigma^{\text{II}}\) (określane jako typ II), również znoszą się na odpowiednio dużej powierzchni i w objętości. Jednak ich wartości dla kolejnych faz, czy w ogólnym przypadku dla \(n\) ziaren (\(\sigma_\alpha^{\text{II}}\), \(\sigma_\beta^{\text{II}}\),…, \(\sigma_n^{\text{II}}\)), osiągają równowagę w obszarze odpowiadającym powierzchniom albo objętościom tych elementów mikrostruktury i ich wartości średnie są zwykle różne od zera (rys. 1.13).
Z uwagi na zakres oddziaływania, do tej grupy naprężeń zaliczane są, opisane już, resztkowe naprężenia cieplne, ale również naprężenia powstałe na skutek przemiany fazowej. Zjawisko takie występuje, gdy w krystalitach, pod wpływem zewnętrznych obciążeń, dochodzi do przemiany polimorficznej (martenzytycznej), która powoduje zmianę rozmiarów komórki elementarnej i wywołuje lokalne odkształcenia. W tworzywach ceramicznych zjawisko to obecne jest w polikryształach i kompozytach zawierających metastabilny, tetragonalny tlenek glinu, który w polu naprężeń poprzedzających wierzchołek pęknięcia przekształca się w odmianę jednoskośną [361–363]. Przejście \(\text{t-ZrO}_{\text{2}}\) w \(\text{m-ZrO}_{\text{2}}\) prowadzi do wzrostu objętości komórki elementarnej i tym samym do powstawania naprężeń ściskających w obszarze przemiany (rys. 1.14). Interakcja pomiędzy indukowanymi w ten sposób naprężeniami a naprężeniami wynikającymi z zewnętrznych obciążeń, powoduje wzrost energii pękania i dzięki temu efektywnie podnosi odporność na kruche pękanie tego typu materiałów [50, 139, 361, 363, 364]. Wzrost ten można wyrazić równaniem [363]: \[\label{eq:trans_tough_KIc} \Delta K_{\text{c}}= \frac{C E^{*}\varepsilon^{\text{tr}} V_f \sqrt{h}}{1 - \nu},\] w którym \(C\) jest stałą zależną od rodzaju procesu zachodzącego w strefie przemiany (przyjmuje wartości od 0.21 do 0.55 [365]), \(E^{*}\) jest efektywnym modułem sprężystości materiału, \(\varepsilon^{\text{tr}}\) jest odkształceniem dylatacyjnym, określającym zmiany objętości wywołane przemianą (\(\varepsilon^{\text{tr}} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33}\)), a \(V_f\) udziałem objętościowym fazy ulegającej przemianie wewnątrz strefy o rozmiarze określonym parametrem \(h\) (rys. 1.14). W zależności od udziału \(\text{t-ZrO}_{\text{2}}\), zastosowanych stabilizatorów, którymi w przypadku tetragonalnego tlenku cyrkonu są najczęściej tlenki: \(\text{Y}_{\text{2}}\text{O}_{\text{3}}\), \(\text{MgO}\) i \(\text{CeO}_{\text{2}}\), jak również rozmiaru strefy przemiany, szacowane umocnienie wywołane tym mechanizmem może powodować wzrost wartości \(K_{\text{Ic}}\) od kilku MPa m1/2 nawet do 10 MPa m1/2 [4, 363].
Wracając do rozmiaru obszarów, w których fluktuacje naprężeń resztkowych równoważą się, należy jeszcze zwrócić uwagę na efekty, wywołane obecnością granic międzyziarnowych, dyslokacji i innych defektów sieci krystalicznej, wynikających z obecności nanometrycznych wtrąceń czy wręcz pojedynczych atomów wbudowanych w strukturę (rys. 1.13). Wartości naprężeń wywołanych tymi zaburzeniami, zmieniają się gwałtownie na przestrzeni nanometrów i wynikają zarówno z niedopasowania geometrycznego, cieplnego, jak i sprężystego elementów będących ich źródłem. Zaliczane są zatem do kolejnego, III typu naprężeń resztkowych i wpływają istotnie na stan granic międzyziarnowych, mogąc stać się bezpośrednim źródłem mikrospękań [139, 186, 202, 260, 260, 366, 367]. Jeśli zaburzenia ulokowane wewnątrz ziaren – modyfikują stan ich naprężeń i tym samym mogą prowadzić do zmiany typu pękania [368–373].
Naprężenia resztkowe III typu, łącznie z naprężeniami typu II, są przedmiotem intensywnych analiz prowadzonych dla polikryształów ceramicznych, zarówno metodami doświadczalnymi jak i symulacyjnymi. W odróżnieniu od tworzyw metalicznych i polimerowych, w których naprężenia te są efektywnie relaksowane poprzez odkształcenie plastyczne, w ceramice stanowią one ważny element opisu właściwości tych materiałów. Przedstawiona tutaj klasyfikacja, może być zatem użyteczna nie tylko w celu uporządkowania rozważań na temat zjawisk mających źródło w zróżnicowaniu właściwości termomechanicznych i procesie otrzymywania tworzyw, ale zastosowane w niej kryterium podziału, wykorzystywane jest również podczas planowania eksperymentów i doboru odpowiednich metod pomiarowych.
Do określania rodzaju naprężeń resztkowych, stosowane są różne kryteria i oznaczenia. Tutaj przyjęta została konwencja oparta na charakterystycznym wymiarze, określającym zasięg naprężeń dla którego ustala się równowaga [por. 12, 353–355].↩︎
Istotny wpływ naprężeń resztkowych na właściwości użytkowe elementów urządzeń, a zarazem duże zapotrzebowanie na wytrzymałe, lekkie i niezawodne materiały służące do ich otrzymywania, spowodowały rozwój szeregu metod doświadczalnych, pozwalających na wyznaczenie wartości tych naprężeń [349, 374]. Metody te można podzielić na niszczące i nieniszczące 28. Metody niszczące opierają się na analizie odkształceń będących skutkiem relaksacji materiału, wywołanej zaburzeniem stanu równowagi wewnętrznej poprzez nacinanie, drążenie lub szlifowanie. Natomiast metody nieniszczące, wykorzystują techniki pozwalające na bezpośredni pomiar odkształceń sprężystych uwięzionych materiale. Zestawienie oraz krótki opis wybranych metod pomiarowych zawierają tabele [1.3] i [1.4].
Jednymi z najbardziej rozpowszechnionych metod pomiaru naprężeń resztkowych, wykorzystywanymi w inżynierii materiałowej, są metody dyfrakcyjne. Pozwalają one na wyznaczanie wartości naprężeń na podstawie pomiarów parametrów sieciowych 29. W materiale polikrystalicznym, w którym obecne są naprężenia resztkowe, odległości międzypłaszczyznowe w krystalitach \(d_{hkl}\), różnią się od wartości wyznaczonych dla idealnych monokryształów w stanie nienaprężonym. Względne odkształcenie płaszczyzn sieciowych można zatem wyrazić jako: \[\label{eq:latice_strain} \langle \varepsilon \rangle_{hkl} = \frac{\langle d \rangle_{hkl} - d_{hkl}^0}{d_{hkl}^0},\] przy czym \(d_{hkl}^0\) jest odległością międzypłaszczyznową odpowiadającą sieci niezdeformowanej. Ponieważ w trakcie pomiaru, dyfrakcja zachodzi dla całej grupy płaszczyzn sieciowych spełniających warunek Braggów, to mierzone w ten sposób odkształcenie jest wartością średnią \(\langle \varepsilon \rangle_{hkl}\). Znając typ struktury krystalicznej badanego materiału oraz wartości składowych tensora podatności sprężystej \(s_{ijkl}\), możliwe jest obliczenie wartości składowych naprężeń resztkowych (\(\varepsilon_{ij} = s_{ijkl} \sigma_{kl}\)) [348, 352, 376, 377].
Odległość międzypłaszczyznowa w nienaprężonym krystalicie (\(d_{hkl}^0\)), stanowi więc wartość referencyjną, pozwalającą na ustalenie odkształcenia względnego, a zatem jest parametrem istotnie wpływającym na dokładność pomiaru. W zależności od zastosowanej techniki, może ona zostać wyznaczona w tym samym pomiarze – obok wartości \(d_{hkl}\), albo stanowić stałą wprowadzaną do obliczeń, której wartość jest określana w niezależnych eksperymentach [354, 378]. W technikach wykorzystujących promieniowanie rentgenowskie, którego głębokość penetracji materiału jest niewielka, przyjmuje się, że naprężenie normalne do powierzchni próbki \(\sigma_{33}\) jest relaksowane poprzez swobodne odkształcenie tej powierzchni. Pozwala to na wyznaczenie wartości \(d_{hkl}^0\) dla płaszczyzn zorientowanych równolegle do płaszczyzny czołowej próbki i określanie naprężeń resztkowych w dwuosiowym stanie naprężeń. Błąd wyznaczenia \(d_{hkl}^0\), popełniany przy takim uproszczeniu, nie przekracza wartości 0.1 % i, w porównaniu do innych źródeł błędów, jest zwykle akceptowalny [352]. Przy zastosowaniu technik pozwalających na pomiary dla trójosiowego stanu naprężeń, opartych zarówno na dyfrakcji promieniowania rentgenowskiego jak i neutronów, błąd taki jest jednak zbyt duży i wartość \(d_{hkl}^0\) wyznaczana jest niezależnie. Najczęściej przeprowadza się w tym celu komplementarne pomiary parametrów sieciowych dla rozdrobnionych próbek analizowanego materiału. Ponieważ luźno rozmieszczone ziarna proszku mogą swobodnie odkształcać się, to wyznaczone dla nich wartości \(d_{hkl}^0\) są obarczone mniejszym błędem [25, 348, 352].
Skupiając się na naprężeniach typu II, które – jak to zostało określone równaniem \eqref{eq:residual_micro_equil} – w odpowiednio dużej objętości próbki równoważą się, należy zwrócić uwagę na dobór rozmiaru analizowanej przestrzeni. Dla metod dyfrakcyjnych, wartość naprężenia \(\sigma^{\text{II}}\) wewnątrz obszaru obejmowanego wiązką, można wyrazić równaniem [348]: \[\label{eq:RSII_vol_avg} \langle \sigma \rangle^{\text{II}} = \frac{1}{V} \int\limits_V \left[ \sigma(x) - \sigma^{\text{I}} \right] \mathop{}\!\mathrm{d}V.\] Taka, objętościowo uśredniona różnica, pomiędzy naprężeniem zależnym od położenia \(\sigma(x)\) a naprężeniem typu I, określa więc wartość średniego naprężenia typu II w analizowanej objętości materiału \(V\). W praktyce, objętość ta powinna być mniejsza od charakterystycznego rozmiaru – dla tego typu naprężeń – rozmiaru krystalitu. W przeciwnym wypadku, wraz ze wzrostem \(V\), wyznaczana wartość \(\langle \sigma \rangle^{\text{II}}\) będzie zdążać do zera [342, 352, 360]. Jednak dla wielu metod dyfrakcyjnych, objętość próbkowanej przestrzeni znacznie przekracza rozmiary krystalitów obecnych w polikrystalicznych tworzywach ceramicznych (rys. 1.15). Wynika to zarówno z głębokości wnikania wiązki, jak i rozdzielczości przestrzennej, która w typowych eksperymentach realizowanych z wykorzystaniem laboratoryjnych źródeł promieniowania rentgenowskiego, mieści się w przedziale od 20 do 100 μm [342] 30. Warto więc zauważyć, że wartości naprężeń resztkowych określone metodami XRD, ale też ND (zob. tab. [1.4] i rys. 1.15) opisują średnie naprężenia dla faz, albo grupy krystalitów o określonej orientacji płaszczyzn sieciowych i nie pozwalają na szczegółową analizę oraz mapowanie wartości naprężeń, występujących wewnątrz poszczególnych krystalitów (por. równ. \eqref{eq:residual_micro_equil}).
Znacznie większą rozdzielczość zapewniają metody opierające się na analizie sygnałów pochodzących z powierzchni próbki. Wymienić tutaj należy metody wykorzystujące dyfrakcję elektronów wstecznie rozproszonych (EBSD, ang. Elektron BackScatter Diffracton), spektroskopię Ramanowską czy mikroskopię fluorescencyjną (rys. 1.15). Osiągane tymi metodami rozdzielczości, dochodzą do wartości submikronowych, a dla HR-EBSD (ang. High Resolution EBSD) nawet do kilku nanometrów [274, 382]. Uzyskiwane w takiej skali dane, stanowią bardzo wartościowy materiał doświadczalny, dający wgląd w stan naprężeń resztkowych skumulowanych wewnątrz krystalitów. W zakresie tworzyw ceramicznych, pomiary takie przeprowadzane są zarówno dla polikryształów jednofazowych [274, 383], jak i kompozytów [384–388]. Zebrane z powierzchni materiału dane, które przedstawiane są często w postaci dwuwymiarowych map rozkładu naprężeń, pozwalają na rozpatrywanie zjawisk w skali pojedynczych krystalitów i tym samym na bezpośrednią analizę związków między mikrostrukturą a właściwościami materiału.
Naprężenia resztkowe zgromadzone na powierzchni próbki, odpowiadają częściowo zrelaksowanemu – dwuosiowemu stanowi naprężeń (\(\sigma_{33} \approx 0\)). Anizotropia właściwości termosprężystych krystalitów, obecność wtrąceń drugiej fazy, przemiany fazowe, a przede wszystkim obróbka powierzchniowa, powodują jednak zaburzenie tego stanu. Dodatkowo, z uwagi na topografię powierzchni i skończoną grubość warstwy pomiarowej, która w wymienionych metodach analizy o dużej rozdzielczości, może sięgać nanometrów, a przy zastosowaniu metod dyfrakcyjnych (XRD) dochodzić do kilkudziesięciu mikrometrów, należy uwzględnić zmianę stanu naprężenia na trójosiowy. Wszystkie te efekty muszą zatem być rozpatrywane podczas planowania eksperymentu oraz późniejszej analizy uzyskiwanych wyników.
W przypadku materiałów ceramicznych, z uwagi na ich dużą twardość oraz kruchość, przygotowanie powierzchni spełniającej warunki wymagane do prawidłowego przeprowadzenia pomiaru, samo w sobie może sprawiać trudności eksperymentalne [389, 390]. Operacje cięcia, szlifowania i polerowania, istotnie wpływają na stan naprężeń obecnych w warstwie powierzchniowej. Wprowadzone w ten sposób do materiału składowe naprężeń, muszą zostać usunięte, co jest osiągane najczęściej poprzez wielogodzinne wygrzewanie w temperaturze zbliżonej do \(T_{\text{sf}}\). Postępowanie takie może jednak prowadzić do zmian właściwości badanego materiału. Dlatego, w zależności od wybranej metody pomiaru naprężeń resztkowych, stosowane są również inne, bardziej zaawansowane techniki przygotowania powierzchni (najczęściej mikro-obszarów) takie jak: trawienie chemiczne, elektrochemiczne, jonowe, plazmowe, ultradźwiękowe czy ablację laserową [389, 390].
Drugim wymienionym efektem, który musi zostać uwzględniony podczas pomiarów, jest grubość warstwy, z której pobierane są informacje strukturalne służące do wyznaczania wartości naprężeń resztkowych. Ma to szczególne znaczenia przy wyznaczaniu RS typu II i III, kiedy istotne stają się fluktuacje wartości, występujące w obszarze porównywalnym do rozmiaru krystalitów – dla ceramiki specjalnej, oznacza to często odległości poniżej mikrometrów. W metodach dyfrakcyjnych, obniżenie intensywności promieniowania docierającego do detektora, zależy eksponencjalnie od odległości płaszczyzn sieciowych od powierzchni próbki. Największy wkład w rejestrowaną intensywność sygnału, będzie miała zatem dyfrakcja zachodząca na płaszczyznach leżących najbliżej powierzchni próbki. Przesuwając się w głąb, intensywność sygnału będzie maleć i w pewnej odległości od powierzchni jego wkład stanie się statystycznie nieistotny. W praktyce przyjmuje się, że efektywna grubość warstwy pomiarowej wyznacza obszar, z którego pochodzi \(2/3\) promieniowania rejestrowanego przez detektor 31 [348, 390]. Grubość ta zależy od rodzaju materiału 32, długości fali i kąta padania promieniowania na powierzchnię próbki. Przy zastosowaniu źródeł promieniowania rentgenowskiego, przyjmuje się, że jest to między 5 a 50 μm [341, 348, 391]. Stosując metody oparte na rozpraszaniu neutronów, grubość efektywna może być znacznie większa i dochodzić nawet do 50 mm jednak uzyskiwana wtedy rozdzielczość jest bardzo ograniczona (\(\sim\)1 mm) [343, 349, 352, 392].
Ponieważ głębokość wnikania wiązki w badany materiał zależy od kąta padania i długości fali, to rejestrując dane przy różnych wartościach tych parametrów, można selektywnie określać naprężenia resztkowe w zależności od odległości od powierzchni próbki [354, 393, 394]. Wyniki tak przeprowadzonych eksperymentów wskazują, że największy gradient naprężeń występuje tuż przy powierzchni [348, 390, 395]. Dodatkowo potwierdzają one istotny wpływ technik stosowanych do przygotowania powierzchni próbek na wyznaczane wartości RS [390, 391, 396].
Stosunkowo nową grupą metod, pozwalających na wyznaczanie wartości naprężeń resztkowych w mikroskali, są metody wykorzystujące przeskalowane techniki relaksacyjne, stosowane tradycyjnie do wyznaczania makronaprężeń własnych (typu I). Główna koncepcja pomiaru pozostaje niezmieniona i opiera się na analizie odkształceń, wywołanych zaburzeniem równowagi wewnętrznej ciała poprzez usunięcie jego części. Wyznaczenie średniego naprężenia resztkowego oraz rozkładu naprężeń w objętości próbki, wymaga rozwiązania problemu odwrotnego, który można zapisać równaniem Volterry pierwszego rodzaju [397]: \[\label{eq:Volterra} d(z) = \int\limits_{z_0}^z g(z,h)\sigma(h)\mathop{}\!\mathrm{d}h,\quad z_0 \leqslant h \leqslant z.\] Deformacja \(d(z)\), która może być wyrażona przemieszczeniem albo odkształceniem, wywołana usunięciem warstwy materiału począwszy od głębokości \(z_0\) (zwykle równej \(0\)) do głębokości \(z\), jest zależna od naprężenia \(\sigma\) skumulowanego w materiale na wszystkich głębokościach \(h\) (w zakresie od \(z_0\) do \(z\)). Funkcja korekcyjna \(g(z,h)\) (kowariancja), opisuje więc podatność deformacji na naprężenie \(\sigma(h)\), występujące na określonej głębokości, przy ograniczonej grubości \(z\) usuwanej warstwy. Zmniejszając rozmiar przestrzeni, w której badany jest stan naprężeń, można zatem uzyskać informacje o fluktuacjach występujących w mikroskali. Takie przeskalowanie wymusza jednak zmianę narzędzi stosowanych do przygotowania próbki oraz sposobów rejestracji i analizy danych pomiarowych. Do nacinania lub drążenia – zaburzenia równowagi wewnętrznej ciała, wykorzystuje się zatem zogniskowaną wiązkę jonów (FIB) 33, a towarzyszące temu przemieszczenia, występujące na powierzchni materiału, rejestrowane są przy pomocy skaningowego mikroskopu elektronowego (SEM). Uzyskane w ten sposób obrazy zrelaksowanej powierzchni, analizowane są metodą cyfrowej korelacji obrazu (DIC, ang. Digital Image Correlation) w odniesieniu do obrazów referencyjnych i ostatecznie, na podstawie symulacji MES, obliczane są wartości naprężeń resztkowych. Procedura ta, podobnie jak w metodach służących do wyznaczania naprężeń w skali makroskopowej, składa się więc z czterech etapów, jednak zastosowane tutaj rozwiązania są specyficzne dla badań prowadzonych w mikroskali.
Rozmiar przestrzeni, która analizowana jest metodami FIB-SEM DIC, zależy od mikrostruktury, właściwości materiału oraz rodzaju naprężeń (ich zasięgu) będących przedmiotem badań. Możliwe jest więc mapowanie odkształceń występujących w obszarze mikrometrów, wywołanych RS typu II, ale również efektów makroskopowych, związanych z obecnością RS typu I, które mogą być rejestrowane dla obszarów o wymiarach sięgających milimetra [380]. Pomiar rozpoczyna się więc od wyboru odpowiedniej powierzchni, z której przy wykorzystaniu działa jonowego, usuwany jest fragment materiału o specyficznym kształcie i głębokości. Najczęściej są to cylindryczne otwory, zespoły szczelin oraz pierścienie. Niekiedy, na powierzchni materiału, nanoszone są dodatkowo znaczniki, umożliwiające kontrolę pozycjonowania (dryftu) lub ułatwiające korelację przemieszczeń obszarów na obrazach [350, 380]. Sekwencja, składająca się z drążenia oraz obrazowania powierzchni, powtarzana jest wielokrotnie, co pozwala na sporządzenie map przemieszczeń przy różnych głębokościach reliefu. Metoda cyfrowej korelacji obrazu, wykorzystywana do sporządzania takich map, została opracowana w latach osiemdziesiątych ubiegłego stulecia i pozwala na bezkontaktowy pomiar odkształcenia [398–400]. W ostatnim dziesięcioleciu, wraz z rozwojem kamer cyfrowych rejestrujących obrazy w wysokiej rozdzielczości, stała się ona uniwersalnym narzędziem, intensywnie wykorzystywanym w inżynierii materiałowej do mapowania ewolucji pól odkształceń, badania propagacji pęknięć oraz walidacji modeli MES [401–406]. W opisywanej metodzie FIB-SEM DIC, rozkład naprężeń resztkowych wewnątrz przestrzeni pomiarowej może zostać ustalony bezpośrednio, techniką cyfrowej korelacji obrazu – najczęściej jednak, wykorzystywane są w tym celu również modele MES. Odwzorowanie geometrii próbki wraz z naniesionym reliefem, umożliwia wyznaczenie parametrów korekcyjnych dla DIC, optymalizację kształtu i rozmiaru przestrzeni pomiarowej oraz walidację uzyskiwanych wyników [350, 380]. Jest to szczególnie istotne dla materiałów polikrystalicznych, których krystality posiadają znaczną anizotropię właściwości termosprężystych, wywołującą niejednorodną deformację powierzchni.
W porównaniu do metod dyfrakcyjnych, metody mikro-relaksacyjne FIB-SEM DIC, pozwalają na badanie stanu naprężenia zarówno dla materiałów krystalicznych, jak i amorficznych. Może to stanowić ważny atut w przypadku eksperymentów prowadzonych dla wielofazowych polikryształów ceramicznych, w których w granicach międzyziarnowych obecna jest faza szklista. Należy jednak zauważyć, że podczas pomiarów wymagających dużej rozdzielczości, przy wyznaczaniu pól naprężeń, których zmienność osiąga równowagę w obszarach pojedynczych, mikrometrycznych krystalitów, zarówno metody dyfrakcyjne jak i mikro-relaksacyjne, pozwalają na ocenę zmienności naprężeń resztkowych jedynie w pobliżu powierzchni. Informacje takie są cenne nie tylko w kontekście naukowo-badawczym, ale również w praktyce inżynierskiej, gdzie mogą posłużyć do prac związanych z poprawą właściwości użytkowych projektowanych oraz optymalizowanych części urządzeń, szczególnie w zakresie kontroli wpływu mechanicznej obróbki powierzchni czy jakości nanoszonych powłok [353, 393, 407].
Rozpatrując natomiast właściwości materiału – wyabstrahowane od kształtu i rozmiaru ciała – zaburzenia powierzchniowe mogą utrudniać analizę zjawisk zachodzących w jego wnętrzu. Zwiększenie objętości pomiarowej, które pozwala na ograniczenie wpływu efektów powierzchniowych, wiąże się jednak zwykle ze zmniejszeniem rozdzielczości przestrzennej rejestrowanych danych. Przykładem może tu być, wspominane już wcześniej, zastosowanie wiązki neutronów w pomiarach dyfrakcyjnych.
Duża rozdzielczość przestrzenna, wymagana do analizy zmienności naprężeń resztkowych w krystalitach, jest również powiązana z dokładnością pomiarów. Uzyskanie jednocześnie żądanego poziomu szczegółowości, przy zachowaniu wysokiej dokładności, jest w praktyce trudne do osiągnięcia. Planowana dokładność jest osiągana zwykle poprzez uśrednianie zebranych w trakcie pomiaru danych, co może prowadzić do zmniejszania rozdzielczości. Z kolei dążenie do uzyskania maksymalnej rozdzielczości, wymaga rejestracji niewielkich różnic pomiędzy sąsiadującymi elementami materiału. W takim przypadku niewielkie błędy popełniane przy wyznaczaniu wartości bezwzględnych dla tych elementów, przekładają się na duże błędy względne – różnice w rejestrowanych wartościach, a tym samym na duże niepewności pomiarowe w ocenie naprężeń [374, 407]. Zwiększanie liczby pomiarów i uśrednianie (wygładzanie) rejestrowanych w ten sposób dużych zbiorów danych, pozwala na jednoczesną poprawę dokładności przy zachowaniu pełnej rozdzielczości oferowanej przez zastosowaną technikę eksperymentalną. Metody nieniszczące wykazują więc w tym względzie przewagę, umożliwiając wielokrotny pomiar tej samej objętości badanego materiału [350, 391], jednak osiągnięcie akceptowalnego poziomu niepewności, może znacząco wydłużać czas trwania eksperymentu i przez to podnosić jego koszt [392].
Przedstawiona specyfika naprężeń resztkowych, wynikająca z ograniczonego zasięgu oddziaływań równoważących się wewnątrz ciała, jak również z różnych źródeł wywołujących te naprężenia, sprawia, że metody pomiaru opierają się głównie na pośredniej ocenie zjawiska, poprzez analizę odkształceń czy relaksacji. Dlatego pomimo opracowania wielu technik doświadczalnych, metody wykorzystywane do określania RS, nie osiągnęły jeszcze poziomu oferowanego przez metody służące wyznaczaniu naprężeń wywołanych zewnętrznym obciążeniem – klasycznych metod stosowanych w badaniach wytrzymałościowych [374].
Metody pomiaru naprężeń resztkowych można pogrupować według różnych kryteriów opartych na przykład o cechy fizyczne – objętość próbki, głębokość penetracji, rozdzielczość, niepewności pomiarowe i rodzaj mierzonych naprężeń, ale również z wykorzystaniem aspektów praktycznych – metody kontaktowe i bezkontaktowe, niszczące lub nieniszczące, koszt i dostępność sprzętu oraz zakres stosowalności – rodzaj materiału, który może zostać poddany badaniu.↩︎
Metody dyfrakcyjne opierają się na związku pomiędzy odległościami międzypłaszczyznowymi w sieci krystalicznej a położeniem refleksów dyfrakcyjnych, opisywanym prawem Braggów: \(n\lambda = 2d\, \sin\theta\) [375]. ↩︎
Rozdzielczość wyrażona jest tutaj najmniejszym wymiarem liniowym przestrzeni, która może zostać rozróżniona przez detektor. Zagadnienie rozdzielczości uzyskiwanej przy pomocy różnych źródeł promieniowania zostanie szerzej opisane w punkcie 2.5.3.2.↩︎
W zależności od stosowanej techniki pomiarowej (geometrii układu) i wykorzystywanej aparatury, wartość ta może być większa – z zakresu 80 %–95 % [352, 354].↩︎
Zjawisko pochłaniania promieniowania przez materiał jest wykorzystywane w metodach tomograficznych i zostanie szerzej omówione w rozdziale 2 (2.5.3.2).↩︎
Technika ta jest również wykorzystywana do trójwymiarowej rekonstrukcji mikrostruktury i zostanie szerzej opisana w rozdziale 2.↩︎
Podczas opisu metod doświadczalnych służących wyznaczaniu naprężeń resztkowych, istotny był przede wszystkim zasięg działania naprężeń i tym samym rozmiar analizowanej przestrzeni oraz uzyskiwana rozdzielczość; źródła pochodzenia naprężeń miały drugorzędne znaczenie. W metodach obliczeniowych kwestie dotyczące wymiarów rozpatrywanej przestrzeni 34, a także – szczególnie w metodach przybliżonych – rozdzielczości, są również istotne, jednak decydującą rolę odgrywają tutaj przyczyny powstawania naprężeń, które narzucają rodzaj obciążeń oraz model materiałowy stosowany do opisu zjawiska. Z uwagi na specyfikę procesu technologicznego oraz właściwości tworzyw ceramicznych, największe znaczenie w tej grupie materiałów mają resztkowe naprężenia cieplne (RTS). Dlatego dalszy opis ukierunkowany będzie na rozwiązania pozwalające analizować stan naprężenia wywołany obciążeniem cieplnym.
Wśród najczęściej wykorzystywanych równań, pozwalających na szacowanie wartości naprężeń resztkowych wynikających z różnic w rozszerzalności cieplnej faz składowych, są równania zaproponowane przez Selsinga [408]. Zostały one wyprowadzone dla modelowego układu składającego się z kulistego wtrącenia otoczonego przez ciągłą osnowę. Przyjmując izotropowe właściwości termosprężyste obydwu faz, Selsing założył, że podczas chłodzenia o \(\Delta T\) na wtrącenie ze strony osnowy będzie wywierane ciśnienie hydrostatyczne \(p\), które wywoła w nim jednorodny stan naprężenia. Wartość tego ciśnienia została przez niego wyrażona jako [408]: \[\label{eq:SelsingP} p = \frac{\Delta \alpha \Delta T}{\dfrac{1 + \nu_o}{2 E_o} + \dfrac{1 - 2 \nu_w}{E_w}},\] przy czym: \(\Delta \alpha\) określa różnicę wartości współczynników rozszerzalności cieplnej osnowy i wtrącenia, \(\Delta T\) różnicę temperatury powodującej skurcz podczas chłodzenia, a \(E_o\), \(\nu_o\) oraz \(E_w\), \(\nu_w\) określają moduł Younga i liczbę Poissona – odpowiednio dla osnowy i wtrącenia. Selsing przyjął również, że jednorodne naprężenie wewnątrz wtrącenia \(\sigma_w\), którego składowa radialna i styczna są sobie równe, będzie, co do wartości, odpowiadać ciśnieniu hydrostatycznemu, lecz będzie miało przeciwny znak (\(\sigma_w = - p\)). Naprężenie w osnowie zostało natomiast opisane trzema składowymi: radialną \(\sigma_r\) i dwiema równymi sobie (co do wartości) składowymi stycznymi \(\sigma_{\theta}\), których wartości będą zależeć od odległości \(r\) od centrum wtrącenia, co można wyrazić równaniem [408]: \[\label{eq:SelsingSigma} \sigma_r = -2\sigma_{\theta} = -p \frac{R^3}{r^3},\] w którym \(R\) jest promieniem wtrącenia. Z zależności tej wynika, że naprężenie radialne w osnowie ma ten sam znak, co naprężenie wewnątrz wtrącenia (\(\sigma_r = \sigma_w\)) i jest równoważone dwiema składowymi naprężenia stycznego o znaku przeciwnym (\(\sigma_r = - 2\sigma_{\theta}\))(rys. 1.16).
Model Selsinga był wielokrotnie weryfikowany dla różnych ceramicznych kompozytów ziarnistych [162, 366, 409, 410]. Obliczone na podstawie równań \eqref{eq:SelsingP} i \eqref{eq:SelsingSigma} wartości naprężeń, wykazują dobrą zgodność z wynikami uzyskiwanymi metodami doświadczalnymi, co potwierdza ich przydatność do szacowania wartości RTS w wielofazowych tworzywach ceramicznych. Ponieważ w równaniach tych wykorzystywane są jedynie podstawowe parametry materiałowe (moduły sprężystości i współczynniki rozszerzalności cieplnej) oraz z uwagi na ich zwięzłą formę, są one często stosowane do szacowania oczekiwanych wartości RTS w trakcie analiz prowadzonych metodami numerycznymi czy w rozważaniach teoretycznych, dotyczących właściwości mechanicznych tworzyw ceramicznych [200, 268, 410–414].
Przyjęcie stałych wartości naprężeń wewnątrz wtrąceń (\(\sigma_w = \mathrm{const}\)), jest jednak dużym uproszczeniem, które szczególnie w przypadku analizy faz wykazujących anizotropię właściwości termosprężystych, może powodować istotne rozbieżności pomiędzy obliczonymi a rzeczywistymi wartościami RTS. Dodatkowe ograniczenie modelu Selsinga wynika z nieuwzględnienia w nim oddziaływań mogących występować pomiędzy sąsiadującymi inkluzjami. Pomimo że naprężenia w osnowie szybko maleją i w odległości \(r = 3R\) od centrum wtrącenia, są już niewielkie (zob. rys. 1.16), to udział objętościowy wtrąceń, dla tak określonego przypadku granicznego, nie może przekraczać 11 % (\(V_{\text{w}}=V_R/V_{3R} = R^3/(3R)^3 = 1/9\)) i to przy założeniu doskonałego ujednorodnienia. Jednak przypadkowe rozmieszczenie wtrąceń w osnowie tworzywa kompozytowego powoduje, że nawet przy niewielkim udziale objętościowym (\(V_{\text{w}}<\)11 %), może dochodzić do lokalnego nakładania się pól naprężeń generowanych wokół niejednorodnie rozproszonych cząstek.
Dokładniejszy opis rozkładu resztkowych naprężeń cieplnych w materiałach kompozytowych można uzyskać, stosując modele uwzględniające interakcje między wtrąceniami. Modele takie rozwinęły się wokół koncepcji przedstawionej pierwotnie przez Eshelby’ego [229, 230], dotyczącej aproksymacji właściwości niejednorodnego ośrodka właściwościami efektywnymi, uzyskanymi na podstawie rozwiązań dla ekwiwalentnej, elipsoidalnej inkluzji umieszczonej w nieograniczonej wymiarowo osnowie. Opierając się na tej koncepcji, Mori i Tanaka [234] opracowali metodę pozwalającą na wyznaczanie średnich naprężeń wewnątrz osnowy w zależności od udziału objętościowego wtrąceń. Stanowiło to istotny krok w rozwoju metod mikromechaniki ośrodków niejednorodnych, pozwalając na wyznaczanie efektywnych właściwości materiałów kompozytowych.
Przedstawione przez nich równania zostały wykorzystane m.in. w pracy Taya i in. [415], zawierającej kompleksowy opis RTS w kompozytach ziarnistych, uwzględniający obecność trzech faz: sferycznych wtrąceń o udziale objętościowym \(V_{\text{w}}\), sferycznych porów o udziale \(V_{\text{p}}\) i osnowy, której udział objętościowy \(V_{\text{o}}= 1 - V_{\text{w}}- V_{\text{p}}\). Średnie naprężenie we wtrąceniu \(\langle \sigma \rangle_{\text{w}}\) i w osnowie \(\langle \sigma \rangle_{\text{o}}\) wywołane chłodzeniem materiału od temperatury spiekania \(T_{\text{S}}\) do temperatury otoczenia \(T_{\text{R}}\), zostało wyrażone przez nich w postaci równań [415]: \[\label{eq:TayaW} \frac{\langle \sigma \rangle_{\text{w}}}{E_{\text{o}}} = \frac{-2 \left( 1 - V_{\text{w}}- V_{\text{p}}\right) \beta \alpha_1^{*}}{A}, \] \[\label{eq:TayaO} \frac{\langle \sigma \rangle_{\text{o}}}{E_{\text{o}}} = \frac{2 V_{\text{w}}\beta \alpha_1^{*}}{A},\] w których współczynniki \(A\) oraz \(\beta\) określone zostały poprzez [415]: \[\begin{aligned} A & = \left( 1 - V_{\text{p}}\right) \left\lbrace\!\left[ 1 - \frac{V_{\text{w}}}{1 - V_{\text{p}}} \right]\!\left( \beta + 2 \right)\!\left( 1 + \nu_{\text{o}} \right) + \frac{3 \beta V_{\text{w}}\left(1 - \nu_{\text{o}}\right) }{1 - V_{\text{p}}}\!\right\rbrace, \\ \beta & = \left( \frac{1+\nu_{\text{o}} }{1 - 2\nu_{\text{w}}} \right)\!\left( \frac{E_{\text{w}}}{E_{\text{o}}} \right),\end{aligned}\] a niedopasowanie odkształceń sprężystych \(\alpha_1^{*}\), powodujące powstawanie naprężeń cieplnych podczas chłodzenia w zakładanym zakresie temperatury (od \(T_{\text{S}}\) do \(T_{\text{R}}\)), wyrazili jako [415]: \[\label{eq:TayaAlphaStar} \alpha_1^{*} = \int\limits_{T_{\text{S}}}^{T_{\text{R}}}\!\left(\alpha_{\text{w}} - \alpha_{\text{o}}\right)\delta\mathop{}\!\mathrm{d}T,\] gdzie symbolem \(\delta\) oznaczona została delta Kroneckera.
Średnie wartości resztkowych naprężeń cieplnych obliczone na podstawie równań \eqref{eq:TayaW} oraz \eqref{eq:TayaO}, przy uwzględnieniu rzeczywistego udziału objętościowego fazy wtrąconej oraz porowatości tworzywa, odpowiadają zatem mikro naprężeniom własnym (RS typu II) skumulowanym w materiale kompozytowym i mogącym wywoływać efekt umocnienia [175, 200, 268, 366, 416–418]. Analiza równań zaproponowanych przez Taya i in. pozwala również zauważyć, że wraz ze wzrostem udziału objętościowego fazy wtrąconej, praktycznie liniowo 35, zmieniają się średnie wartości resztkowych naprężeń cieplnych – zarówno dla wtrąceń jak i dla osnowy (rys. 1.17). W przypadku, gdy współczynnik rozszerzalności cieplnej wtrąceń jest większy od współczynnika rozszerzalności cieplnej osnowy (\(\alpha_{\text{w}} > \alpha_{\text{o}}\)), jak na przykład w kompozycie \(\text{SiC-TiB}_{\text{2}}\), przy niewielkim udziale objętościowym fazy wtrąconej, naprężenia rozciągające wewnątrz wtrąceń (\(\langle \sigma \rangle_{\text{w}}>0\)) przyjmują wartości maksymalne, by stopniowo maleć ze wzrostem \(V_{\text{w}}\). Natomiast w osnowie, naprężenia ściskające (\(\langle \sigma \rangle_{\text{o}}< 0\)) przy małym udziale objętościowym wtrąceń są niewielkie, ale wraz z jego wzrostem ich wartości stają się istotne. W przypadku odwrotnym, gdy \(\alpha_{\text{w}} < \alpha_{\text{o}}\) (np. w kompozycie \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\text{-WC}\)), odpowiednie relacje między naprężeniami a udziałem objętościowym wtrąceń są zachowane, lecz zmienia się znak RTS dla wtrąceń i osnowy (rys. 1.17).
Szczegółowa analiza rozkładu resztkowych naprężeń cieplnych wymaga jednak uwzględnienia również kształtu wtrąceń. Zagadnienie to zostało przeanalizowane przez Hsueha i Bechera [419, 420]. Wykorzystując koncepcję Eshelby’ego oraz rozwiązania opracowane przez Moriego i Tanakę, Hsueh i Becher rozpatrzyli zależność wartości naprężeń we wtrąceniu od jego kształtu. Uzyskane przez nich rozwiązanie, opierało się na zmodyfikowanym modelu elipsoidalnej inkluzji o kształcie określonym przez trzy półosie – dwie o długości \(a\) i trzecią o długości \(c\) (rys. 1.18). Na podstawie ogólnej zależności określającej wartości składowych naprężenia wewnątrz ziarna, Hsueh i Becher wyznaczyli zwięzłe, analityczne związki dla trzech specyficznych kształtów wtrąceń: dysków – gdy stosunek \(c/a\), będący współczynnikiem kształtu, zdążał do zera (\(a \gg c\)), kul – jeśli \(c/a = 1\) oraz włókien przy założeniu, że \(c/a\) zdążał do nieskończoności (\(c \gg a\)).
Hsueh i Becher przyjęli, że dla dysków, z uwagi na znikomą grubość w kierunku zgodnym z półosią \(c\), naprężenia normalne do powierzchni dysku (\(\sigma_{33}\)), zarówno we wtrąceniu jak i w osnowie, muszą być równe zero. Natomiast naprężenia w kierunku równoległym do półosi \(a\), wewnątrz inkluzji (\(\sigma_{11}\)), zostały wyrażone równaniem [419, 420]: \[\label{eq:HsuehBecherDisk} \sigma_{11} = \frac{\left(\alpha_{\text{o}} - \alpha_{11}\right) \Delta T}{ \dfrac{1 - \nu_{\text{w}}}{E_{\text{w}}} + \dfrac{V_{\text{w}}\left( 1 - \nu_{\text{o}}\right)}{\left( 1 - V_{\text{w}}\right)E_{\text{o}}}},\] w którym \(\alpha_{11}\) jest osiowym współczynnikiem rozszerzalności cieplnej dla wtrącenia. Równocześnie wartość naprężenia w osnowie \(\sigma_{11(\text{w})}\) wynika z warunku równowagi mechanicznej, który można zapisać równaniem [419, 420]: \[\label{eq:HsuehBecherDiskMatrix} V_{\text{w}}\sigma_{11} + \left( 1 - V_{\text{w}}\right) \sigma_{11(\text{w})} = 0.\]
Rozpatrując kuliste inkluzje, Hsueh i Becher przyjęli izotropię rozszerzalności cieplnej fazy wtrąconej (\(\alpha_{\text{w}} = \left( 2\alpha_{11} + \alpha_{33} \right)/3\)), co z kolei pozwoliło wyrazić naprężenie cieplne w inkluzji, poprzez naprężenie hydrostatyczne [419, 420]: \[\label{eq:HsuehBecherSpher} \sigma_{11} = \sigma_{22} = \sigma_{33} = \frac{\left(\alpha_{\text{o}} - \alpha_{\text{w}}\right) \Delta T}{\dfrac{1}{3 \mathcal{K}_{\text{w}}} + \dfrac{1}{4\left(1 - V_{\text{w}}\right) \mathcal{G}_{\text{o}}} +\dfrac{V_{\text{w}}}{3\left(1 - V_{\text{w}}\right)\mathcal{K}_{\text{o}}}},\] przy czym \(\mathcal{K}_{\text{w}}\) i \(\mathcal{K}_{\text{o}}\) są tutaj modułami ściśliwości odpowiednio dla wtrąceń i osnowy, a \(\mathcal{G}_{\text{o}}\) modułem sprężystości poprzecznej osnowy.
Dla trzeciego przypadku, który odpowiadał inkluzjom w kształcie włókna (\(c \gg a\)), wartości naprężeń cieplnych we wtrąceniu, w kierunkach zgodnych z krótkimi półosiami \(a\) (\(\sigma_{11}\) i \(\sigma_{22}\)) oraz w kierunku długiej osi \(c\) (\(\sigma_{33}\)) zostały przez Hsueha i Bechera wyrażone poprzez [419, 420]: \[\label{eq:HsuehBecherFiber11} \begin{gathered} \sigma_{11} = \sigma_{22} = A \left\lbrace\! \left[ \frac{1}{E_{\text{w}}} + \frac{V_{\text{w}}}{\left( 1-V_{\text{w}}\right) \!E_{\text{o}}} \right] \!\left(\alpha_{\text{o}}-\alpha_{11}\right) + \right. \\ \left. + \left[ \frac{\nu_{\text{w}}}{E_{\text{w}}} + \frac{V_{\text{w}}\nu_{\text{o}}}{\left( 1 - V_{\text{w}}\right)\!E_{\text{o}}} \right]\!\left(\alpha_{\text{o}} - \alpha_{33} \right) \!\right\rbrace \Delta T, \end{gathered}\] \[\label{eq:HsuehBecherFiber33} \begin{gathered} \sigma_{33} = A \left\lbrace 2\!\left[ \frac{\nu_{\text{w}}}{E_{\text{w}}} + \frac{V_{\text{w}}\nu_{\text{o}}}{\left( 1 - V_{\text{w}}\right) \!E_{\text{o}}} \right] \!\left(\alpha_{\text{o}}-\alpha_{11}\right) + \right. \\ \left. + \left[\frac{1 - \nu_{\text{w}}}{E_{\text{w}}}+\frac{1 + V_{\text{w}}+ \left(1 - V_{\text{w}}\right)\!\nu_{\text{o}}}{\left( 1 - V_{\text{w}}\right)\!E_{\text{o}}}\right]\!\left(\alpha_{\text{o}} - \alpha_{33} \right)\!\right\rbrace \Delta T, \end{gathered}\] gdzie \(\alpha_{11}\) i \(\alpha_{33}\) są osiowymi współczynnikami rozszerzalności cieplnej dla wtrącenia oraz \(A\) określone jest jako [419, 420]: \[\begin{gathered} \label{eq:HsuehBecherFiberA} A = \left[ \frac{\left(1+\nu_{\text{w}}\right)\left(1-2\nu_{\text{w}}\right)} {{E_{\text{w}}}^2} + \frac{V_{\text{w}}\left(2 - \nu_{\text{w}} - \nu_{\text{o}} - 4\nu_{\text{w}}\nu_{\text{o}}\right) + 1 + \nu_{\text{o}}} {\left(1 - V_{\text{w}}\right)E_{\text{w}} E_{\text{o}}} \right. \\ \left. + \frac{V_{\text{w}}\left(1 + \nu_{\text{o}}\right) \left(1 + V_{\text{w}}- 2V_{\text{w}}\nu_{\text{o}}\right)} {\left(1-V_{\text{w}}\right)^2{E_{\text{o}}}^2} \right]^{-1}\end{gathered}\] Średnie naprężenie w osnowie \(\langle \sigma \rangle_{\text{o}}\), zawierającej wtrącenia o kształcie kulistym albo włóknistym, można określić z warunku równowagi mechanicznej [419, 420]: \[\label{eq:HsuehBecherMatrix} \langle \sigma \rangle_{\text{o}}= \frac{-V_{\text{w}}\langle \sigma \rangle_{\text{o}}}{1-V_{\text{w}}},\] w którym \(\langle \sigma \rangle_{\text{o}}\) oznacza średnie naprężenie we wtrąceniu (\(\langle \sigma \rangle_{\text{o}}= (2\sigma_{11} + \sigma_{33})/3\)).
W odróżnieniu od rozwiązań przedstawionych przez Taya i in. [415], w których zakładane były izotropowe właściwości zarówno osnowy jak i wtrąceń, Hsueh i Becher [419, 420] wprowadzili do przedstawionych powyżej równań (\eqref{eq:HsuehBecherDisk}, \eqref{eq:HsuehBecherSpher}, \eqref{eq:HsuehBecherFiber11}, \eqref{eq:HsuehBecherFiber33}) osiowe współczynniki rozszerzalności cieplnej. Pozwoliło to na częściowe uwzględnienie anizotropii wtrąceń, przy zachowaniu zwięzłej formy analitycznych równań opisujących składowe naprężenia. Pomimo uproszczeń dotyczących właściwości termosprężystych osnowy, Hsueh i Becher wykazali silną zależność pomiędzy kształtem ziaren fazy wtrąconej a wartościami i rozkładem resztkowych naprężeń cieplnych. Analiza wyprowadzonych przez nich równań wskazuje, że deformacja kształtu wtrąceń, prowadzi do istotnej zmiany wartości składowych naprężenia (rys. 1.19). W przypadku trzech opisanych geometrii, największe zróżnicowanie pomiędzy składowymi RST występuje w inkluzjach dyskowych. Silne wypłaszczenie takich wtrąceń, które można zaobserwować w wielu polikrystalicznych tworzywach ceramicznych, prowadzi, z jednej strony, do spadku wartości składowej naprężenia normalnego do powierzchni, ale z drugiej, do wyraźnego wzrostu wartości składowych równoległych do płaszczyzny wypłaszczenia. Z kolei jednoosiowe wydłużenie wtrąceń powoduje, że składową o większej wartości naprężenia staje się składowa leżąca wzdłuż długiej osi inkluzji (włókna). Można również zauważyć (rys. 1.19), że dla wydłużonych wtrąceń relacje pomiędzy wartościami składowych naprężenia stabilizują się przy stosunku długości \(c/a = 5\).
Równania wyprowadzone na podstawie zmodyfikowanej koncepcji Eshelby’ego, zarówno przez Taya i in. [415] (\eqref{eq:TayaW}, \eqref{eq:TayaO}) jak i przez Hsueha i Bechera [419,420] (\eqref{eq:HsuehBecherDisk}, \eqref{eq:HsuehBecherSpher}, \eqref{eq:HsuehBecherFiber11}, \eqref{eq:HsuehBecherFiber33}), można sprowadzić do równań zaproponowanych przez Selsinga [408] (\eqref{eq:SelsingP}, \eqref{eq:SelsingSigma}), przy założeniu \(V_{\text{w}}= 0\) [421]. Jednak w przeciwieństwie do modelu opartego na izolowanych wtrąceniach, zastosowanego przez Selsinga, modele Taya i in. oraz Hsueha i Bechera, wykorzystujące efektywne właściwości sprężyste ośrodków niejednorodnych (uwzględniające skończony udział objętościowy wtrąceń), pozwalają znacznie poszerzyć zakres stosowalności przedstawionych przez nich rozwiązań analitycznych. Szczególnie w przypadku materiałów zawierających amorficzną osnowę (materiałów szkło-ceramicznych), w której naprężenie jest jednorodne, zgodność wyników obliczeń z wartościami wyznaczonymi metodami doświadczalnymi jest bardzo dobra aż do 30 %-owego udziału objętościowego fazy wtrąconej, a niekiedy, przy równomiernym rozproszeniu wtrąceń, nawet do 60 %-obj. [422–426].
W przypadku polikrystalicznych tworzyw ceramicznych, założenie dotyczące izotropii właściwości termosprężystych faz, może stanowić jednak tylko pierwsze przybliżenie. W wielu ceramicznych kompozytach ziarnistych, zarówno wtrącenia jak i ziarna osnowy, z uwagi na strukturę krystaliczną odbiegającą od regularnej (zob. p. 1.1, tab. [tab:MatCeramKryszt] ), wykazują wyraźną anizotropię właściwości termomechanicznych, prowadzącą do lokalnego wzrostu niedopasowania odkształceń sprężystych. Opisywane, proste rozwiązania analityczne, wywodzące się z koncepcji Eshelby’ego (modele pola średniego), wykorzystują aproksymację właściwości niejednorodnego ośrodka właściwościami efektywnymi. Właściwości te, w kontekście statystycznym, są więc momentami pierwszego rzędu (wartościami oczekiwanymi) dla pola naprężenia czy odkształcenia. Niosą zatem jedynie ograniczoną informację o tych polach, która nie uwzględnia lokalnych niejednorodności. Tym samym, cały szereg problemów związanych ze zróżnicowaniem kształtu krystalitów, jak również rozkładem naprężeń w osnowie i wtrąceniach oraz wpływem naprężeń powstających na skutek przyłożonych zewnętrznych obciążeń, nie może być rozwiązany za pomocą tego typu modeli [177, 427]. W celu uzyskania pełniejszej informacji statystycznej, pozwalającej na opis rozkładu wartości naprężeń i odkształceń, niezbędne jest wyznaczenie momentów wyższych rzędów (miar rozproszenia).
Podstawy teoretyczne rozwiązań umożliwiających wyznaczenie fluktuacji wartości resztkowych naprężeń cieplnych (macierzy kowariancji RTS) dla modeli opierających się na teorii pola średniego (MFT, ang. Mean Field Theory), zostały sformułowane w pracach: Ortiza i Molinariego [428], Krehera [429], Krehera i Molinariego [430], Buryachenko i Krehera [431]. Zbudowane na tej podstawie modele stochastyczne pozwalają na badanie rozkładu RTS z uwzględnieniem zmienności kształtu i orientacji krystalitów oraz przypadkowego rozproszenia wtrąceń w kompozytach. Rozwiązania tak postawionego zagadnienia, uzyskiwane są jednak zwykle metodami numerycznymi [432–435].
Aby zilustrować koncepcję modeli stochastycznych, można przytoczyć rozwiązanie zaproponowane przez Ma i in. [436], dla kompozytu zawierającego fazę anizotropową, którą stanowi trygonalny tlenek glinu (\(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\)) oraz izotropową, będącą regularną odmianą tlenku cyrkonu (\(\gamma\text{-ZrO}_{\text{2}}\)). W takim układzie, średnią wartość naprężenia dla ziaren \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\), wyrazić można momentem pierwszego rzędu wyznaczonym z rozkładu naprężenia w całej rozpatrywanej populacji krystalitów [436]: \[\label{eq:avgRTSaluMa1994} \langle \sigma_{ij} \rangle_{\!\text{A}} = \langle \sigma_{ij}^i \rangle_{\!\text{A}} + \langle \sigma_{ij}^a \rangle_{\!\text{A}}.\] Średnie naprężenie w ziarnach \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) (\(\langle \sigma_{ij} \rangle_{\!\text{A}}\)), jest więc dane kombinacją dwóch komponentów: izotropowego \(\langle \sigma_{ij}^i \rangle_{\!\text{A}}\) i anizotropowego \(\langle \sigma_{ij}^a \rangle_{\!\text{A}}\). Komponent izotropowy opisuje naprężenie uśrednione po wszystkich orientacjach krystalitów \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) obecnych w rozpatrywanej populacji i odpowiada za oddziaływanie z izotropową fazą \(\text{ZrO}_{\text{2}}\). Dodatkowo jest on związany warunkiem równowagi mechanicznej \eqref{eq:HsuehBecherMatrix} ze średnim naprężeniem w fazie cyrkoniowej. Natomiast komponent anizotropowy, określa naprężenie wynikające z różnej orientacji względnej sąsiadujących ze sobą ziaren o anizotropowych właściwościach termomechanicznych.
Komponent izotropowy \(\langle \sigma_{ij}^i \rangle_{\!\text{A}}\) można wyrazić równaniem [436]: \[\label{eq:avgRTSaluIsoMa1994} \langle \sigma_{ij}^i \rangle_{\text{A}} = \sigma_{\text{A}} \delta_{ij},\] w którym \(\delta_{ij}\) jest deltą Kroneckera, a naprężenie cieplne \(\sigma_{\text{A}}\), można określić na podstawie efektywnego modułu ściśliwości \(\mathcal{K}^{*}\) oraz udziału objętościowego fazy \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) (\(V_{\text{A}}\)), jako [436]: \[\label{eq:avgRTSaluIsoSigmaMa1994} \sigma_{\text{A}} = -3 V_{\text{A}} \mathcal{K}^{*}(\alpha_{\text{A}} - \alpha_{\text{Z}}) \Delta T,\] przy czym \(\alpha_{\text{A}}\) i \(\alpha_{\text{Z}}\) są współczynnikami rozszerzalności cieplnej odpowiednio dla fazy \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\) i \(\gamma\text{-ZrO}_{\text{2}}\). Z kolei wartość \(\mathcal{K}^{*}\) dana jest wyrażeniem [429, 436]: \[\label{eq:Keff} \mathcal{K}^{*}= \frac{ \mathcal{K}_{\text{Z}} \mathcal{K}_{\text{A}} } { \mathcal{K}_{\text{A}} V_{\text{A}} + \mathcal{K}_{\text{A}} V_{\text{A}} n_{\text{Z}} + \mathcal{K}_{\text{A}} n_{\text{Z}} + \mathcal{K}_{\text{Z}} V_{\text{Z}} n_{\text{Z}} },\] w którym: \(\mathcal{K}_{\text{Z}}\) i \(\mathcal{K}_{\text{A}}\) są modułami ściśliwości (oznaczenia faz składowych takie jak dla rozszerzalności cieplnej), a współczynnik \(n_{\text{Z}}\) zależy od liczby Poissona dla fazy cyrkoniowej: \(n_{\text{Z}} = 2\left(1 - 2 \nu_{\text{Z}} \right)/\left( 1 + \nu_{\text{Z}} \right)\).
Komponent anizotropowy \(\langle \sigma_{ij}^a \rangle_{\!\text{A}}\), będący momentem pierwszego rzędu dla pola naprężenia wywołanego przez niedopasowanie między różnie zorientowanymi (anizotropowymi) ziarnami tlenku glinu, można wyrazić dla trzech składowych naprężenia związanych z kierunkami krystalograficznymi, równaniami [436]: \[\label{eq:avgRTSaluAniso11Ma1994} \langle \sigma_{11}^a \rangle = \langle \sigma_{22}^a \rangle = \tfrac{2}{3} \mathcal{G}_{\text{E}} \left(\alpha_c - \alpha_a \right)\Delta T \equiv \langle \sigma_a^a \rangle,\] \[\label{eq:avgRTSaluAniso33Ma1994} \langle \sigma_{33}^a \rangle = - \tfrac{4}{3} \mathcal{G}_{\text{E}} \left(\alpha_c - \alpha_a \right)\Delta T \equiv \langle \sigma_c^a \rangle,\] w których: \[\label{eq:avgRTGeMa1994} \mathcal{G}_{\text{E}} = \frac{ \mathcal{G}_{\text{A}} \left( 9 \mathcal{K}_{\text{A}} + 8 \mathcal{G}_{\text{A}} \right) } {5 \left( 3 \mathcal{K}_{\text{A}} + \mathcal{G}_{\text{A}} \right)},\] oraz \(\mathcal{G}_{\text{A}}\) jest modułem sprężystości poprzecznej (\(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)).
W celu analitycznego wyznaczenia momentu drugiego rzędu dla statystycznego rozkładu resztkowych naprężeń cieplnych \(\langle \sigma_{ij}\sigma_{ij} \rangle\) opisującego ich fluktuacje przestrzenne, Ma i in. [436] przyjęli, że przy niewielkiej wzajemnej korelacji dwóch komponentów pól naprężeń (izotropowego i anizotropowego, rozdzielonych równaniem \eqref{eq:avgRTSaluMa1994}), moment \(\langle \sigma_{ij}\sigma_{ij} \rangle\) może w przybliżeniu zostać wyrażony, jako suma momentów drugiego rzędu dla obydwu komponentów [436]: \[\label{eq:secOrdSum} \langle \sigma_{ij}\sigma_{ij} \rangle = \langle \sigma_{ij}^i\sigma_{ij}^i \rangle + \langle \sigma_{ij}^a\sigma_{ij}^a \rangle.\] Dodatkowo, aby rozwiązać analitycznie powyższe równanie, Ma i in. ograniczyli swoje rozważania jedynie do trzech głównych składowych naprężenia, których kierunki są zgodne z kierunkami sieci krystalicznej \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\). Dzięki takim uproszczeniom, do wyznaczenia wartości momentu drugiego rzędu dla komponentu izotropowego, zostały zastosowane granice Hashina–Shtrikmana [231, 232], które wprowadzono w miejsce efektywnego modułu ściśliwości w równaniu \eqref{eq:avgRTSaluIsoSigmaMa1994}. W ten sposób rozrzut komponentu izotropowego został wyrażony granicznymi wartościami naprężenia cieplnego \(\sigma_{\text{A}}^+\) i \(\sigma_{\text{A}}^-\).
Do wyznaczenia momentu drugiego rzędu dla komponentu anizotropowego, zależnego od orientacji, Ma i in. wykorzystali zależności wyprowadzone przez Krehera [429], wiążące \(\langle \sigma_{ij}^a\sigma_{ij}^a \rangle\) z wariacjami tensora odkształceń cieplnych [429, 436]: \[\label{eq:anisoVarMa1994} \langle \sigma_{ij}^a\sigma_{ij}^a \rangle = 3 \langle s^{a\,\text{II}} \rangle + \langle s_{ij}^a s_{ij}^a \rangle,\] które dane są zależnościami: \[\label{eq:anisoVarSsMa1994} \langle s^{a\,\text{II}} \rangle = \frac{2}{90}\frac{\left(12 \mathcal{K}_{\text{A}} \mathcal{G}_{\text{A}} \right)^2}{\left( 3\mathcal{K}_{\text{A}}+4\mathcal{G}_{\text{A}} \right)^2} \left( \alpha_c - \alpha_a \right)^2 \Delta T^2, \] \[\label{eq:anisoVarSssMa1994} \langle s_{ij}^a s_{ij}^a \rangle = \tfrac{8}{15}\mathcal{G}_{\text{A}}^2 \frac{27 \mathcal{K}_{\text{A}}^2 + 48 \mathcal{K}_{\text{A}}\mathcal{G}_{\text{A}} + 32\mathcal{G}_{\text{A}}^2} {\left( 3\mathcal{K}_{\text{A}}+4\mathcal{G}_{\text{A}} \right)^2} \left( \alpha_c - \alpha_a \right)^2 \Delta T^2,\]
Wprowadzone w przedstawionym rozwiązaniu problemu założenia i szereg uproszczeń, pozwoliły Ma i in. [436] wyznaczyć, na podstawie prostych zależności analitycznych, momenty pierwszego i drugiego rzędu dla rozkładu resztkowych naprężeń cieplnych w badanym materiale kompozytowym. Model stochastyczny, który opracowali, został zweryfikowany w oparciu o dane empiryczne uzyskane z pomiarów RTS metodą PS (zob. tab. [1.4]). Możliwość szybkiego, statystycznego opisu rozkładu RST, spowodowała że, model ten i inne opierające się na cytowanych już pracach [428–431, 436], są często wykorzystywane podczas analizy danych doświadczalnych uzyskanych metodami spektroskopowymi (Raman i PS) [387, 437–439].
W rozważaniach dotyczących wytrzymałości czy odporności na pękanie, istotna jest również możliwość analizy zmian rozkładu naprężeń wywołanych obecnością sąsiadujących wtrąceń. Problem ten jest zwykle badany poprzez superpozycję pól naprężeń generowanych wokół ekwiwalentnych, elipsoidalnych inkluzji [432, 440, 441]. Stosowane w tym celu rozwiązania opierają się często na modelu dwufazowego kompozytu składającego się z kulistego wtrącenia o promieniu \(a\) otoczonego kulistą osnową o promieniu \(b\), który został pierwotnie zaproponowany przez Fahmyego i Ragaia [442] do modelowania rozszerzalności cieplnej kompozytów ziarnistych. Liu i Winn [443] wykorzystując związki analityczne Fahmyego i Ragaia, opisujące pole odkształceń wokół pojedynczego wtrącenia, wyznaczyli naprężenie równowagowe występujące w granicy międzyfazowej [443]: \[\label{eq:LiuWinnInterfaceSigma} \sigma_{\text{gb}} = \frac{\left(\alpha_{\text{o}}- \alpha_{\text{w}}\right) \Delta T} {\dfrac{2a^3\left(1-2\nu_{\text{o}}\right)+b^3\left(1+\nu_{\text{o}}\right)} {2E_{\text{o}}\left( b^3 - a^3 \right)} + \dfrac{1 - 2\nu_{\text{w}}}{E_{\text{w}}}}.\] W porównaniu do wcześniej przedstawionych równań, udział objętościowy wtrąceń został ujęty tutaj za pomocą promieni wtrącenia i osnowy, ale w rozpatrywanej kulistej przestrzeni \((a/b)^3 = V_{\text{w}}\).
Tak określone \eqref{eq:LiuWinnInterfaceSigma} naprężenie równowagowe występujące w granicy międzyfazowej \(\sigma_{\text{gb}}\), posłużyło następnie do wyznaczenia składowych naprężenia: radialnej \(\sigma_r\) i stycznej \(\sigma_{\theta}\) – w zależności od odległości \(r\) od środka inkluzji [443]: \[\begin{aligned} \sigma_r &= \sigma_{\text{gb}}\, \frac{a^3\!\left(b^3 - r^3\right)}{r^3\!\left(a^3 - b^3\right)}, \label{eq:LiuWinnSigmaR}\\ \sigma_{\theta} &= - \sigma_{\text{gb}}\, \frac{a^3\!\left(2r^3 + b^3 \right)}{2r^3\!\left(a^3-b^3\right)}, \label{eq:LiuWinnSigmaS}\end{aligned}\] przy czym: \(r = a + \delta r\), a \(\delta r\) było odległością od granicy międzyfazowej.
Przyjmując, że dominującą rolę w kształtowaniu rozkładu naprężeń w osnowie będą miały najbliżej położone, bezpośrednio sąsiadujące ze sobą wtrącenia, Liu i Winn rozszerzyli opis do układu zawierającego dwa stykające się obszary zawierające inkluzje (rys. 1.20). W układzie tym, wartości składowych naprężenia zostały wyrażone poprzez kombinację liniową odpowiednich składowych dla izolowanych inkluzji: \(\sigma_r^A + \sigma_r^B = \sigma_r^{AB}\) oraz \(\sigma_{\theta}^A + \sigma_{\theta}^B = \sigma_{\theta}^{AB}\).
Analizując wyprowadzone równania, Liu i Winn zauważyli, że efekt spowodowany nakładaniem się składowych radialnych naprężenia jest niewielki i szybko zanika wraz ze zmniejszającym się udziałem objętościowym fazy wtrąconej. Autorzy tłumaczyli ten fakt małym zasięgiem działania składowej \(\sigma_r\), który ogranicza się do odległości nieprzekraczającej dwóch promieni inkluzji. Natomiast ocena składowych stycznych, ujawniła obecność wyraźnego efektu wynikającego z interakcji między inkluzjami. Efekt ten nasilał się, w przybliżeniu liniowo, wraz ze wzrostem udziału objętościowego wtrąceń. Liu i Winn rozważali również wpływ rozmiaru wtrąceń na wartości naprężeń w oddzielającej je osnowie i ustalili, że przy stałym udziale objętościowym \(V_{\text{w}}\), zmiana rozmiaru sąsiadujących inkluzji nie wpływa na wartość naprężeń generowanych w osnowie.
Przedstawione wnioski, wpisują się w główny nurt rozważań dotyczących rozkładu resztkowych naprężeń cieplnych w tworzywach wielofazowych. Do podobnych ustaleń doszli również inni autorzy, wykorzystujący analityczne zależności opisujące interakcję między wtrąceniami [432, 440, 441, 444, 445]. Wszystkie one wskazują na istotny wpływ udziału objętościowego, odległości międzyziarnowych, ale również względnych rozmiarów inkluzji oraz ich kształtu, na wartości naprężeń i ich rozkład w materiałach kompozytowych. Jednak bezpośrednia weryfikacja doświadczalna wyników tych prac jest nadal ograniczona. Bardzo duża rozdzielczość wymagana do ilościowej kontroli uzyskiwanych analitycznie rezultatów, która dla polikrystalicznych tworzyw ceramicznych powinna sięgać nanometrów, jest aktualnie trudna do osiągnięcia przy akceptowalnym poziomie błędu pomiarowego. Dlatego najczęściej rezultaty porównywane są z wynikami obliczeń uzyskanymi metodami przybliżonymi [257, 268, 273, 432, 435, 446–448]. Metody te – najczęściej metoda elementów skończonych i metody pokrewne – pozwalają dodatkowo na analizę układów o złożonej geometrii, odbiegającej od prostych, regularnych kształtów ziaren, które stanowią podstawę rozważań analitycznych. Umożliwia to wierniejsze odwzorowanie specyficznych cech morfologicznych, szczególnie przy wykorzystaniu dwuwymiarowych modeli geometrycznych zbudowanych na podstawie mikrofotografii wykonanych przy pomocy SEM, albo modeli opartych na trójwymiarowych rekonstrukcjach mikrostruktury (zob. rozdz. 2). W ostatnim dwudziestoleciu, modele takie zostały opracowane dla wielu polikrystalicznych tworzyw ceramicznych, a rosnące zainteresowanie metodami przybliżonymi, w kontekście analizy RTS, związane jest nie tylko z możliwością opisu złożonych kształtów, anizotropii oraz losowej orientacji ziaren w polikrysztale. Nie bez znaczenia jest również coraz większa dostępność dużej mocy obliczeniowej i oprogramowania tworzonego przez społeczność akademicką, wspomagającego najbardziej pracochłonne etapy przygotowania modeli obliczeniowych.
Pierwsze prace dotyczące modelowania rozkładu resztkowych naprężeń cieplnych w ceramicznych materiałach polikrystalicznych, prowadzone metodą elementów skończonych, zostały opublikowane na przełomie lat 80. i 90. ubiegłego stulecia 36. Początkowo opierały się one na prostych, dwuwymiarowych modelach geometrycznych, w których powierzchnia polikryształu reprezentowana była regularnie ułożonymi ziarnami o heksagonalnym kształcie [257, 452]. W latach 90. zaczęto stosować również trójwymiarowe modele uzyskane poprzez teselację Voronoı̈a [453]. Wyniki symulacji prowadzonych na zespołach kilkuset krystalitów, pozwoliły zauważyć, że losowe rozmieszczenie anizotropowych ziaren w tworzywach ceramicznych może powodować tworzenie rozległych pól naprężeń obejmujących swoim zasięgiem wiele krystalitów. Przewidywania oparte zatem na prostych modelach deterministycznych, mogą znacznie odbiegać od rzeczywistego rozkładu RTS i nie być reprezentatywne dla całej zbiorowości krystalitów składających się na rozpatrywaną objętość tworzywa [271, 452]. Dlatego do pełnego opisu resztkowych naprężeń cieplnych, oprócz wartości średnich składowych naprężenia, niezbędne jest również uwzględnienie ich fluktuacji występujących pomiędzy sąsiadującymi ziarnami, a wyniki muszą być uzyskane na podstawie odpowiednio dużej próby statystycznej (liczby ziaren, objętości), mogącej zapewnić reprezentatywność uzyskiwanych wartości RTS dla analizowanego tworzywa.

W symulacjach numerycznych, opierających się na modelach geometrycznych odwzorowujących mikrostrukturę, stosowane są aktualnie różne koncepcje w zależności od ilości i jakości informacji dotyczących budowy analizowanego materiału. W przypadku materiałów wielofazowych, gdy średni rozmiar ziaren jednej z faz jest znacznie mniejszy od rozmiarów ziaren pozostałych faz, albo gdy pełna segmentacja dla wszystkich faz nie jest w praktyce możliwa 37, często stosowanym uproszczeniem jest rozpatrywanie takiej fazy jako ośrodka ciągłego o właściwościach izotropowych. Niekiedy takie założenie przyjmowane jest dla wszystkich faz budujących analizowane tworzywo. Jest to najczęściej podyktowane brakiem informacji o orientacji przestrzennej krystalitów, albo wspomnianymi już trudnościami z segmentacją. Pomimo takich uproszczeń, przeprowadzone dla ceramicznych kompozytów ziarnistych symulacje, pozwalają uzyskać jakościowy i ilościowy opis rozkładu resztkowych naprężeń cieplnych przy uwzględnieniu morfologii podstawowych elementów mikrostruktury (rys. 1.21).
Przykładem prac opierających się na założeniu izotropii wszystkich faz obecnych w tworzywie, mogą być symulacje RTS przeprowadzone przez Hsueha i in. [446]. Model obliczeniowy został w nich przygotowany na podstawie obrazów mikrostruktury \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), w którym izolowane azotkowe ziarna otoczone były fazą amorficzną. Uzyskane wyniki symulacji MES pozwoliły autorom zauważyć, że znak naprężeń resztkowych (rozciągające, ściskające), obecnych w fazie rozdzielającej ziarna \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), jest uwarunkowany nie tylko różnicą właściwości termomechanicznych między fazami, ale również wynika z konfiguracji ziaren.
Materiałem kompozytowym na bazie \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) zajmowali się również Bao i in. [445]. Analizowali oni wpływ dodatku wtrąceń \(\text{TiN}\) na wartości RTS. W ich dwuwymiarowym modelu zakładającym izotropię faz składowych, wtrącenia \(\text{TiN}\) zostały przybliżone kolistymi kształtami o różnych promieniach. Pomimo tak znacznych uproszczeń zastosowanych podczas symulacji MES, zauważyli oni, że uzyskane średnie wartości RTS są niższe niż odpowiednie wartości obliczone analitycznie. Efekt ten powiązali z częściową relaksacją naprężeń, wynikającą z ograniczonych wymiarów przestrzeni rozpatrywanej w trakcie symulacji, co lepiej odpowiada rzeczywistym warunkom obciążeń w jakich znajduje się materiał.
Symulacje RTS z wykorzystaniem metody elementów skończonych, przy założeniu izotropii faz składowych, zostały przeprowadzone także dla kompozytów węglikowych. Grabowski i in. [454, 455] rozpatrywali zależność pomiędzy mikrostrukturą a rozkładem naprężeń w kompozytach \(\text{SiC-TiB}_{\text{2}}\) otrzymanych różnymi metodami syntezy w szerokim zakresie udziału objętościowego wtrąceń borkowych. Obrazy powierzchni przekrojów rozpatrywanych materiałów, uzyskane przy pomocy SEM, zostały poddane jakościowej i ilościowej analizie mikrostruktury, a następnie posłużyły do wykonania modeli geometrycznych, na podstawie których prowadzone były symulacje MES. Na podstawie uzyskanych wyników, autorzy potwierdzili występowanie jakościowej zależność pomiędzy rozkładem naprężeń cieplnych w kompozytowej osnowie a rozmiarem, kształtem i względnym rozmieszczeniem ziaren fazy wtrąconej.
Szereg opublikowanych prac, w których zakładana była izotropia faz składowych, dotyczyła również analizy rozkładu RTS w kompozytach z osnową tlenku glinu czy tlenku cyrkonu. Bućko i in. [186] analizowali kompozyt \(\text{ZrO}_{\text{2}}\text{-Al}_{\text{2}}\text{O}_{\text{3}}\) i, na podstawie przeprowadzonych symulacji MES opartych na modelach geometrycznych odwzorowujących rzeczywiste kształty wtrąceń, zauważyli znaczny wpływ krzywizny korundowego wtrącenia na bezwzględną wartość naprężenia w cyrkoniowej osnowie. Pędzich i Grabowski [260, 261, 367] badali także kompozyty z osnową \(\text{ZrO}_{\text{2}}\) i \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) zawierające wtrącenia węglika wolframu oraz metalicznego wolframu. Opracowane przez nich modele pozwoliły na wykonanie symulacji dla badanych układów i na jakościową analizę wpływu RTS na obserwowane w tych tworzywach umocnienie.
Założenie dotyczące izotropii faz składowych wraz z przyjęciem dwuwymiarowych modeli geometrycznych istotnie zmniejsza koszt obliczeniowy. Dlatego niektóre prace, ujmujące dodatkowo zjawisko mikropękania, które relaksuje częściowo naprężenia cieplne, wykorzystują te założenia w celu skrócenia czasu niezbędnego do przeprowadzenia obliczeń. Przykładowo, takie analizy dla kompozytów \(\text{Al}_{\text{2}}\text{O}_{\text{3}}\text{-SiC}_{\text{nano}}\) przeprowadzili Zhou i Yi [456]. Uzyskane przez nich wyniki symulacji MES wykazały bardzo dobrą zgodność z przewidywaniami teoretycznymi dotyczącymi krytycznego rozmiaru ziaren niezbędnego do wystąpienia mikrospękania (por. równ. \eqref{eq:Cleveland-Bradt} [269, 270]). W analizowanych przez nich układach, rozmiary nanometrycznych krystalitów węglika krzemu nie przekraczały krytycznego rozmiaru \(D_{\text{c}}\) i tym samym nie wywołały zjawiska mikropękania. W swojej pracy zwrócili oni jednak uwagę na potrzebę dokładniejszego opisu zarówno właściwości faz – uwzględniającego anizotropię, jak i geometrii – poprzez trójwymiarowe odwzorowanie ziaren w polikrysztale.
Częściowe włączenie anizotropii do opisu właściwości (przynajmniej w odniesieniu do wybranych faz budujących kompozyt) można znaleźć w pracach Gubernat i in. [168] oraz Grabowskiego [202], dotyczących analizy właściwości kompozytów o osnowie \(\text{SiC}\) zawierających od 1 do 10 % wag. wtrąceń w postaci pirografitu. Bardzo duża różnica pomiędzy wartościami osiowych współczynników rozszerzalności cieplnej dla wtrąceń grafitowych 38, nie pozwalała na wykorzystanie w modelu obliczeniowym wartości średniej współczynnika rozszerzalności cieplnej i traktowania tej fazy jako izotropowej. Przyjmując dwuwymiarową geometrię modelu, autorzy analizowali kolejno różne orientacje grafitowych wtrąceń. Pozwoliło to na określenie rozkładu RTS w węglikowej osnowie pomiędzy grafitowymi wtrąceniami i umożliwiło wyjaśnienie mechanizmu tworzenia mikrospękań, widocznych na obrazach wykonanych przy pomocy transmisyjnej mikroskopii elektronowej (TEM).
W przypadku materiałów wielofazowych, których jedną z faz jest faza amorficzna, przyjęcie w symulacjach RTS założenia o izotropii właściwości termomechanicznych jest w pełni uzasadnione – pod warunkiem, że skład tej fazy nie zmienia się znacząco. Przykładem takiego tworzywa może być \(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\) spiekany w obecności fazy tlenkowej, która otacza wydłużone ziarna azotkowe, a przy większym udziale objętościowym, tworzy ciągłą osnowę. W modelach numerycznych uwzględniających trójwymiarową geometrię tworzywa, anizotropowa faza azotkowa (o strukturze heksagonalnej) charakteryzowana jest zwykle odpowiednimi stałymi sprężystości i osiowymi współczynnikami rozszerzalności cieplnej, a fazie tlenkowej przypisywane są właściwości izotropowe. Przykładem prac, w których zastosowano taki opis faz, może być monografia Wipplera [458], w której przedstawił on algorytm pozwalający na trójwymiarową rekonstrukcję mikrostruktury azotku krzemu oraz przeprowadził szereg symulacji pozwalających na wyznaczenie rozkładu RTS jak również na analizę pękania tego materiału. Zagadnieniem rozkładu resztkowych naprężeń cieplnych w \(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\) zajmowali się również Othmani i in. [177]. Ich model skonstruowany został w oparciu o dane doświadczalne uzyskane techniką FIB-SEM (zob. p. 2.5.2.1). Na podstawie przeprowadzonych analiz, potwierdzili oni ogólne wnioski Wipplera, dotyczące podatności fazy amorficznej na mikropękanie wynikające z dużej koncentracji naprężeń w tej fazie. Dodatkowo zauważyli, że fluktuacje naprężeń cieplnych w ziarnach \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) maleją wraz ze wzrostem rozmiaru ziaren. Podobne rezultaty symulacji uzyskali również Dubiel i in. [178], analizując rozkład RTS w materiale składającym się z krystalitów \(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\) o zróżnicowanym rozmiarze, otoczonych z fazą tlenkową. W pracy tej przeanalizowane zostały dodatkowo kompozyty \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) oraz \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\). Trójwymiarowe modele geometryczne, odwzorowujące mikrostrukturę rozpatrywanych tworzyw, uzyskano metodą przypadkowego ciasnego upakowania (RCP). Wyniki symulacji zostały skonfrontowane z wartościami RTS uzyskanymi na podstawie pomiarów XRD. Pozwoliło to na szczegółowy opis rozkładu przestrzennego RTS w analizowanych materiałach azotkowych i wskazanie źródeł rozbieżności pomiędzy wykorzystanymi metodami badawczymi.
Symulacje procesu powstawania resztkowych naprężeń cieplnych w jednofazowych polikryształach ceramicznych wymagają zastosowania precyzyjnego opisu właściwości termomechanicznych na poziomie pojedynczych krystalitów. Opis taki powinien uwzględniać symetrię krystalitów i wynikającą z niej anizotropię, jak również orientację przestrzenną osi krystalograficznych względem głównego układu odniesienia związanego z całym rozpatrywanym ciałem (próbką). Wśród pierwszych prac dotyczących materiałów ceramicznych, w których uwzględnione zostały wymienione czynniki, można wyróżnić prace Zimmermanna i in. [271] oraz Vedula i in. [272]. Analizowali oni rozkład RTS w polikrystalicznym \(\alpha\text{-Al}_{\text{2}}\text{O}_{\text{3}}\). Dwuwymiarowe modele geometryczne zostały uzyskane przez nich różnymi metodami. Zimmermann i in. posłużyli się syntetycznymi mikrostrukturami wygenerowanymi przy pomocy metody Monte Carlo (zob. p. 2.6.3), natomiast Vedula i in. oparli się na rzeczywistych obrazach mikrostruktury, wykorzystując w tym celu SEM wyposażony w detektor EBSD, który pozwolił zebrać informacje o orientacji krystalitów obecnych na obrazie. Wyniki symulacji przeprowadzonych przez obydwie grupy badawcze, metodą elementów skończonych przy założeniu chłodzenia o \(\Delta T =\)−1500 °C, były zbliżone i wskazywały na szeroki rozkład wartości naprężeń cieplnych. Szczególnie duża fluktuacja wartości naprężeń obserwowana była w granicach międzyziarnowych. Wynikało to z anizotropii właściwości krystalitów, która w połączeniu z ich przypadkową orientacją, prowadziła do lokalnego niedopasowania właściwości termomechanicznych, powodującego powstawanie naprężenia podczas chłodzenia.
Naprężenia cieplne w polikrystalicznym tlenku glinu (\(\alpha\text{-Al}_{\text{2}}\text{O}_{\text{3}}\)) analizowali również Niezgoda i in. [459]. W wykorzystanych przez nich trójwymiarowych modelach geometrycznych, kształt krystalitów został przybliżony prostymi bryłami przestrzennymi (czternastościanami Kelvina, sześcianami oraz osiemnastościanami), a do opisu właściwości materiału przyjęli oni ortotropię rozszerzalności cieplnej i izotropię sprężystości. Porównanie wyników symulacji, przeprowadzonych dla różnych kształtów krystalitów, pozwoliło im wykazać, że szczególnie efektywnymi koncentratorami naprężeń są krawędzie i naroża ziaren. Taka obserwacja była w pełni zgodna z wcześniejszymi pracami z zakresu mikromechaniki, jak również wieloma danymi doświadczalnymi, ale wyraźnie wskazywała potrzebę dokładniejszego opisu morfologii krystalitów stosowanego w modelach numerycznych. Niezgoda i in. przeprowadzili również ilościową analizę rozkładu naprężeń, w której zastosowali metody statystyczne analogiczne do metod używanych tradycyjnie do analizy wyników eksperymentalnych. Pozwoliło to między innymi zauważyć istotny wpływ warunków brzegowych na uzyskiwane numerycznie wartości naprężeń cieplnych.
Kolejnym przykładem analizy rozkładu RTS w jednofazowych polikryształach ceramicznych, przeprowadzonej metodą elementów skończonych, może być praca Berdin i in. [460]. Autorzy rozpatrywali dwie odmiany polimorficzne tlenku cyrkonu: jednoskośną \(\alpha\text{-ZrO}_{\text{2}}\) i tetragonalną \(\beta\text{-ZrO}_{\text{2}}\). Syntetyczna mikrostruktura polikryształów, wykorzystana w trójwymiarowym modelu geometrycznym, została uzyskana metodą teselacji Voronoı̈a, a właściwości termomechaniczne przyjęte w obliczeniach MES, uwzględniały anizotropię krystalitów. Uzyskane wyniki symulacji, wskazały istotne różnice w wartościach i rozkładzie RTS, występujące pomiędzy badanymi materiałami. Wyraźnie szerszy rozrzut wartości naprężeń obecny był w jednoskośnym \(\alpha\text{-ZrO}_{\text{2}}\). W materiale tym, różnice pomiędzy krystalitami w wartościach naprężeń maksymalnych obecnych wewnątrz ziaren, sięgały aż 30 % w zależności od orientacji względem sąsiednich krystalitów. Wyniki te potwierdziły zatem istotny wpływ anizotropii na naprężenia cieplne w jednofazowych materiałach polikrystalicznych.
Dokładny opis właściwości termomechanicznych faz uwzględniający anizotropię oraz orientację względną poszczególnych krystalitów, jest również stosowany w przypadku wielofazowych polikryształów ceramicznych. Przykładem może być tutaj praca Grabowskiego i Pędzicha [273, 338] dotycząca kompozytu \(\text{SiC-TiB}_{\text{2}}\). W pracy tej autorzy rozpatrywali wpływ kształtu ziaren oraz anizotropii na rozkład resztkowych naprężeń cieplnych. Do symulacji MES wykorzystali oni dwuwymiarowe modele geometryczne oparte na obrazach mikrostruktury oraz modele uzyskane poprzez częściową modyfikację geometrii, polegającą na podziale wydłużonych krystalitów \(\text{SiC}\), tak aby uzyskać izometryczne kształty ziaren osnowy. W przeprowadzonych analizach numerycznych autorzy wykorzystywali zarówno pełny opis właściwości, opierający się na wartościach współczynników sztywności (\(C_{\alpha,\beta}\)) oraz osiowych współczynnikach rozszerzalności cieplnej (\(\alpha_a\) i \(\alpha_c\)), jak i na obliczonych na ich podstawie wartościach średnich, które zastosowali w analizach opartych na założeniu izotropii właściwości faz składowych. Uzyskane przez nich wyniki symulacji uwidoczniły silną zależność między anizotropią właściwości termomechanicznych faz a wartościami i rozkładem RTS oraz mniej istotne różnice wynikające z geometrii krystalitów.
Dwuwymiarowy model numeryczny oparty na rzeczywistej mikrostrukturze został wykorzystany również we wspomnianej już monografii Niezgody i in. [459]. Na podstawie obrazów powierzchni przekrojów kompozytu \(\text{Al}_{\text{2}}\text{O}_{\text{3}}\text{-ZrO}_{\text{2}}\), zawierającego 30 %-obj. tetragonalnego tlenku cyrkonu stabilizowanego tlenkiem itru (3Y-TZP), autorzy przygotowali modele geometryczne, w których poszczególne krystality posiadały losowo zorientowane osie krystalograficzne. Zastosowanie skorygowanych wartości współczynników rozszerzalności cieplnej dla wybranych ziaren 3Y-TZP pozwoliło autorom symulować obok zjawiska resztkowych naprężeń cieplnych, przemianę martenzytyczną, do której może dochodzić w rozpatrywanym kompozycie.
Opublikowane w ostatnich latach prace, dotyczące kompozytów z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) – \(\text{ZrO}_{\text{2}}\), coraz częściej ujmują opis właściwości granic międzyziarnowych. Zwykle stosowany jest w tym celu model strefy kohezyjnej, pozwalający uwzględnić relaksację naprężeń poprzez tworzenie mikrospękań (zob. p. 1.3.5). Przykładowo, analizę rozkładu resztkowych naprężeń cieplnych z zastosowaniem CZM przeprowadzili Kim i in. [461]. Dwuwymiarowy model geometryczny, przygotowany na podstawie obrazów mikrostruktury, posłużył do symulacji numerycznych dla kompozytu \(\text{Al}_{\text{2}}\text{O}_{\text{3}}\text{-ZrO}_{\text{2}}\) zawierającego 10 %-obj. wtrąceń cyrkoniowych. Przedstawiony przez autorów model pozwolił im na prześledzenie procesu powstawania mikrospękań, wywołanych obecnością RTS oraz obciążeniami cyklicznych, symulującymi procesy zmęczeniowe w analizowanym polikrysztale.
Przedstawione w tej części prace, wykorzystujące metodę elementów skończonych do określania rozkładu resztkowych naprężeń cieplnych w tworzywach ceramicznych, stanowią tylko niewielki ułamek badań, które zostały zrealizowane w tym zakresie. Niektóre z zasygnalizowanych rozwiązań, zostaną jeszcze opisane szerzej w rozdziale 4, jednak zawarte tutaj przykłady i tak mogą być jedynie ilustracją wybranych metod służących do analizy rozpatrywanego zjawiska. Warto jednak zauważyć, że aktualnie stosowane modele numeryczne osiągnęły już poziom zaawansowania pozwalający na uzyskiwane wyników symulacji zbieżnych z danymi doświadczalnymi. Możliwość obniżania i kontrolowania błędu, na przykład poprzez selektywne zagęszczanie siatek w metodzie elementów skończonych czy stopniowe zwiększanie rozmiaru analizowanych obszarów, prowadzi do uzyskania dużej dokładności analiz. Niezależne badania prowadzone metodami przybliżonymi (MES i metodami pokrewnymi), coraz częściej określane są więc mianem eksperymentów numerycznych. Ponadto błędy pomiarowe, wynikające z konieczności przygotowania próbek do badań doświadczalnych nie zakłócają wyników analiz numerycznych ale mogą zostać celowo w nich uwzględnione. Dlatego metody przybliżone powszechnie stosowane są na etapie kalibracji oraz weryfikacji metod doświadczalnych służących do wyznaczania naprężeń resztkowych takich jak: FIB-SEM, DIC [342, 462–464], metod opartych na efekcie Ramana [385, 465], metod dyfrakcyjnych [342, 378, 466] oraz HD [451].
Zagadnienie dotyczące rozmiaru przestrzeni analizowanej metodami obliczeniowymi, zostanie szerzej omówione w rozdziale 3.4.↩︎
Liniowa zmiana średnich wartości resztkowych naprężeń cieplnych wynika z przyjętego warunku równowagi mechanicznej i zakładanej stałej porowatości – niezależnie od składu kompozytu. Jednak w rzeczywistych tworzywach wielofazowych udział objętościowy porów zwykle związany jest ze składem tworzywa i udziałem niektórych faz mogących ułatwiać zagęszczanie podczas spiekania.↩︎
Należy zauważyć, że metody przybliżone były stosowane już wcześniej do analizy naprężeń cieplnych w skali makroskopowej (RTS typu I), szczególnie w zakresie zagadnień spawalniczych, w metodach doświadczalnych służących wyznaczaniu RTS, czy w ogólniejszym ujęciu, do opisu zjawiska termosprężystości [449–451].↩︎
Metody stosowane do uzyskiwania informacji o budowie mikrostrukturalnej materiałów polikrystalicznych – w tym segmentacja, która jest jednym z etapów podczas analizy danych pomiarowych (analizy obrazu) – zostaną omówione w rozdziale 2 (p. 2.3, 2.5).↩︎
W kierunku prostopadłym do warstw grafitowych (zgodnie z osią krystalograficzną \(c\)) średnia wartość współczynnika rozszerzalności cieplnej w zakresie pomiędzy temperaturą spiekania a temperaturą pokojową wynosi 20–28 × 10−6 K−1, a w kierunku równoległym do płaszczyzn (zgodnie z osią \(a\)) 0–1 × 10−6 K−1 [457].↩︎
Intensywny rozwój metod pozwalających na wyznaczanie wartości naprężeń resztkowych ma swoje źródło nie tylko w aspekcie czysto poznawczym, ale przede wszystkim jest związany z istotnym wpływem tych naprężeń na właściwości makroskopowe materiałów, a tym samym na końcowe cechy użytkowe wyrobów – części i współpracujących ze sobą elementów maszyn. W tworzywach ceramicznych, jak to już wcześniej było podkreślane, decydujące znaczenie mają naprężenia resztkowe powstające podczas chłodzenia materiału po procesie syntezy – resztkowe naprężenia cieplne. Ich obecność i rola, była również zaznaczana w poprzednich podrozdziałach, podczas omawiania wybranych właściwości polikrystalicznych tworzyw ceramicznych i ich związków z cechami mikrostruktury. Dlatego tutaj zostaną zebrane i szerzej omówione najważniejsze efekty wynikające z obecności RTS, które wpływają na kluczowe dla ceramiki, właściwości mechaniczne: wytrzymałość i odporność na pękanie. Warto również zauważyć, że obecność resztkowych naprężeń w polikryształach ceramicznych jest permanentną cechą tych tworzyw. O ile wiele cech mikrostruktury, takich jak rozmiar, kształt ziaren czy porowatość, jesteśmy już w stanie kontrolować i świadomie kształtować, to niedopasowanie właściwości termosprężystych występujące pomiędzy sąsiadującymi krystalitami i będące bezpośrednią przyczyną powstawania RTS, jest ściśle związane ze składem fazowym tworzywa. Dlatego ich obecność jest nieunikniona i musi być uwzględniana na etapie projektowania i optymalizacji właściwości polikrystalicznych materiałów ceramicznych.
Najlepiej widocznym efektem, wynikającym z obecności RTS, jest spontaniczne mikropękanie. Zjawisko to, w granicznej formie, może prowadzić do powstawania makroskopowych spękań, utraty spoistości materiału, a niekiedy wręcz uniemożliwiać uzyskanie litego tworzywa [214, 467–471]. Najczęściej jednak, skumulowane w materiale naprężenia resztkowe nie wywołują w nim aż tak ewidentnych zmian i ich obecność ujawnia się dopiero w momencie przyłożenia zewnętrznego obciążenia.
Jeden z pierwszych modeli analitycznych, opisujących zjawisko mikropękania, został opracowany przez Davidge’a i Greena [472]. Zauważyli oni, że podczas chłodzenia materiału, magazynowana w nim energia odkształceń sprężystych (\(U_{\text{e}}\)), zależy od objętości wtrąceń (por. równ. \eqref{eq:SelsingSigma}). Dodatkowo, w analizowanych przez nich kompozytach, dla których rozszerzalność cieplna osnowy była mniejsza od rozszerzalności cieplnej kulistych wtrąceń (\(\alpha_{\text{o}}< \alpha_{\text{w}}\)), powstające mikrospękania układały się centrycznie, tworząc półsferyczne szczeliny przy granicy międzyfazowej (rys. 1.22a). Na tej podstawie, energię potrzebną na utworzenie nowych powierzchni (mikropęknięć) \(U_{\text{s}}\), powiązali z promieniem kulistych wtrąceń \(R\), przyjmując, że \(U_{\text{s}}= 2 A \gamma = 4\pi R^2 \gamma\). Następnie, korzystając z tak określonych składowych energii \(U_{\text{e}}\) i \(U_{\text{s}}\) oraz warunku energetycznego: \(U_{\text{e}}> U_{\text{s}}\), który musi zostać spełniony aby mogły powstawać nowe powierzchnie, Davidge i Green wyznaczyli krytyczną wartość promienia wtrącenia \(R_\text{c}\), powyżej której może zachodzić proces mikropękania [472]: \[\label{eq:R_c-Davidge-Green} R_\text{c} \geqslant \frac{8\gamma}{p^2\left[\dfrac{1+\nu_{\text{o}}}{E_{\text{o}}}+\dfrac{2\left(1-2\nu_{\text{w}}\right)}{E_{\text{w}}}\right]},\] przy czym \(p\) jest tutaj ciśnieniem równoważnym naprężeniu radialnemu \(\sigma_r\), wyznaczonemu na podstawie równania Selsinga \eqref{eq:SelsingSigma}.
Na podstawie warunku energetycznego \(U_{\text{e}}> U_{\text{s}}\), koniecznego (lecz niewystarczającego) do wystąpienia zjawiska mikropękania powstało szereg modeli analitycznych [269, 270, 414, 443, 473–477]. Wspomniany już wcześniej model Clevelanda i Bradta [269] (zob. równ. \eqref{eq:Cleveland-Bradt}) oraz jego analiza przeprowadzona przez Evansa i Faber [270], pozwoliły na wyznaczenie granicznych wartości średnic krystalitów w jednofazowych polikryształach ceramicznych, przy których dochodzić może do spontanicznego lub wymuszonego przez propagującą szczelinę mikropękania 39. Opisane w literaturze rozwiązania, dotyczą również szerokiej gammy materiałów kompozytowych o różnych relacjach między rozszerzalnością cieplną faz składowych oraz szybkościami uwalniania energii dla ziaren \(G_\text{g}\) i granic międzyziarnowych \(G_\text{gb}\). Krytyczną wartość średnicy wtrącenia \(D_{\text{c}}\), przy której dochodzi do spontanicznego mikropękania w kompozycie ziarnistym, wyznaczyli Liu i Winn [443]. Posługując się przedstawionym już wcześniej modelem \eqref{eq:LiuWinnInterfaceSigma} oraz energetycznym warunkiem pękania, ustalili, że [443]: \[\label{eq:Dc_LiuWinn} D_{\text{c}}> \frac{6\gamma^{*}}{ \left[ \left( F_r^2 + 2 F_{\theta}^2 \right) - 2\nu_{\text{o}} F_{\theta} \left( 2F_r + F_{\theta} \right) \right] \dfrac{2\sigma^2}{E_{\text{o}}} +\dfrac{\sigma^2\left( 1-2\nu_{\text{w}}\right)^2}{E_{\text{w}}} }.\] W równaniu tym \(\gamma^{*}\) oznacza efektywną energię powierzchniową osnowy (\(\gamma^{*}\approx\)1 J/m2), \(\sigma\) odpowiada wartości naprężenia wyznaczonego z równania \eqref{eq:LiuWinnInterfaceSigma}, a \(F_r\) i \(F_{\theta}\) są odpowiednio radialnym i stycznym współczynnikiem zależnym od udziału objętościowego wtrąceń, które mogą zostać obliczone analitycznie lub wyznaczone eksperymentalnie dla analizowanego kompozytu.
Warto również zaznaczyć, że wartości \(D_{\text{c}}\) wyznaczane mogą być także metodami numerycznymi [257, 447, 452]. Takie podejście pozwala na zwiększenie złożoności rozpatrywanej geometrii, lepsze odwzorowanie mikrostruktury i tym samym na bardziej realistyczny opis zjawiska mikropękania.
Wniosek płynący z analizy wyników prac teoretycznych, znajdujących potwierdzenie w eksperymentach prowadzonych dla polikrystalicznych tworzyw ceramicznych, dotyczy możliwości ograniczenia spontanicznego mikropękania poprzez zmniejszenie rozmiaru krystalitów. Okazuje się bowiem, że bardzo duże wartości resztkowych naprężeń cieplnych, lokalnie mogące przekraczać makroskopową wytrzymałość materiału, nie muszą prowadzić do spontanicznego rozwoju mikrospękań, szczególnie w przypadku materiałów kompozytowych, w których wraz ze wzrostem udziału objętościowego fazy wtrąconej rośnie wartość \(D_{\text{c}}\) [44, 158, 364, 443]. Zmniejszenie zatem rozmiaru krystalitów poniżej wartości krytycznej, może prowadzić do kumulacji RTS, które zostaną zrelaksowane dopiero w strefie procesowej – w pobliżu propagującej szczeliny. Taki stan naprężeń może zwiększyć odporność na pękanie, nie wpływając istotnie na wytrzymałość tworzywa. Ilustracją mogą być tutaj prace Evansa i Faber [270, 478] czy Hutchinsona [479], w których została zawarta szczegółowa analiza wpływu spontanicznego oraz wymuszonego mikropękania na odporność na pękanie.
Podwyższenie oporu stawianego przez materiał na rozprzestrzenianie się pęknięcia (\(R^{\text{m}}/R\)), wynikające z tworzenia się siatki mikrospękań w pobliżu wierzchołka propagującej szczeliny, można wyrazić jako [92]: \[\label{eq:MicroShielding} \frac{R^{\text{m}}}{R} = 1 + \frac{2 \Omega^{\text{m}} V_{\text{f}}\varepsilon^{\text{m}} E^{*}} {\sigma_c^{\text{m}}}\] przy czym: \(\Omega^{\text{m}}\) jest współczynnikiem kształtu strefy, w której zachodzi mikropękanie, \(V_{\text{f}}\) to udział objętościowy krystalitów mogących ulegać pękaniu (\(V_{\text{f}}\approx 1\)), \(\varepsilon^{\text{m}}\) wyraża lokalne odkształcenie cieplne (\(\varepsilon^{\text{m}} \approx \frac{1}{2} \Delta \alpha \Delta T\) [269]), \(E^{*}\) jest efektywnym modułem sprężystości, a \(\sigma_c^{\text{m}}\) to krytyczna wartość naprężenia powodującego mikropękanie.
Zgodnie z powyższym równaniem \eqref{eq:MicroShielding}, wzrost oporu stawianego przez materiał w trakcie pękania, wynikający z tworzenia strefy, w której generowane są mikrospękania, jest tym większy im mniejsza jest wartość \(\sigma_c^{\text{m}}\). Wzrostu tego można zatem oczekiwać, aż do granicy spontanicznego mikropękania, gdy \(\sigma_c^{\text{m}} \rightarrow 0\). Łącząc to z odpornością na pękanie, można stwierdzić, że w polikryształach o drobnoziarnistej mikrostrukturze, gdy przekroczony zostanie minimalny rozmiar ziaren niezbędny do wystąpienia (wymuszonego) mikropękania \(D_{\text{min}}\) \eqref{eq:Cleveland-Bradt} należy spodziewać się umocnienia materiału. Umocnienie to będzie rosło wraz ze wzrostem rozmiaru krystalitów. Gdy rozmiary krystalitów przekroczą \(D_{\text{c}}\), spontanicznie pojawiające się w materiale mikrospękania, spowodują stopniowe obniżanie odporności na pękanie [44, 364, 478]. Opisana zależność między odpornością na pękanie a rozmiarem krystalitów została przedstawiona na rysunku 1.23. Należy jednak zauważyć, że obecność resztkowych naprężeń cieplnych w materiale nie jest konieczna do wystąpienia w nim mikropękania, które jest również obserwowane w polikryształach o strukturze regularnej.
Opisane zjawisko mikropękania wpływa także na szereg innych właściwości. Powstające podczas chłodzenia mikropęknięcia koncentrują naprężenia i rozrastając się, mogą osiągać rozmiar wad krytycznych. Obniża to wytrzymałość oraz niezawodność materiału (skraca średni czas upływający do wystąpienia uszkodzenia), szczególnie w przypadku długotrwałych obciążeń statycznych albo obciążeń cyklicznych (zob. p. 1.2.2) [480, 481].
Częściowa relaksacja naprężeń poprzez mikropękanie, powoduje również obniżenie energii sprężystej skumulowanej w materiale i, podobnie jak porowatość, zmniejsza względną wartość modułu sprężystości (\(E_n = E/E_0\), por. p. 1.3.4). Dla polikrystalicznych tworzyw ceramicznych, obniżenie wartości \(E_n\) można bezpośrednio powiązać z udziałem objętościowym materiału, w którym występują mikrospękania \(V_{\text{mp}}\), zależnością sformułowaną przez Sałganika [482]: \[\label{eq:Emicrocrack} E_n = \frac{1}{1 + A V_{\text{mp}}},\] w której \(A\) jest współczynnikiem obliczonym na podstawie liczby Poissona (\(\nu_0\)) niespękanego materiału [482]: \[A = \frac{16\left(10 -3\nu_0\right)\left(1-\nu_0^2\right)} {45\left(2-\nu_0\right)}.\] Dla wartości \(\nu_0\) z zakresu od 0 do 0.5, współczynnik \(A\) przyjmuje wartości odpowiednio od 1.78 do 1.51. Oszacowany na tej podstawie efekt, wywołany obecnością mikrospękań mogących tworzyć się w trakcie obciążania, jest zatem istotny, ponieważ już przy wartości \(V_{\text{mp}}=\)0.1 redukuje wartość modułu Younga o \(\sim\)15 %. Zjawisko to można zaobserwować na przykład podczas statycznej próby rozciągania, jako stopniową zmianę nachylenia krzywej naprężenie–odkształcenie [52, 483, 484] (rys. 1.24).
Jednak w wielu polikrystalicznych tworzywach ceramicznych, warunek tworzenia mikrospękań nie zostaje osiągnięty. Drobnoziarnista mikrostruktura, stosunkowo duża energia pękania ziaren i granic międzyziarnowych, niewielka anizotropia rozszerzalności cieplnej krystalitów albo, w przypadku materiałów wielofazowych, zbliżone właściwości termomechaniczne faz, sprawiają, że zjawisko mikropękania praktycznie nie występuje. Pomimo tego lokalne fluktuacje resztkowych naprężeń cieplnych mogą nadal, w trakcie pękania, stanowić barierę dla propagujących szczelin, które rozprzestrzeniają się w materiale zgodnie z warunkiem minimum energii.
Związek pomiędzy rozkładem RTS a kierunkiem propagacji szczelin został jakościowo opisany we wcześniej cytowanej już pracy Davidge’a i Greena [472]. Zwrócili oni uwagą, że w kompozytach ziarnistych, w których wtrącenia posiadają większą rozszerzalność cieplną niż osnowa (\(\alpha_{\text{w}}> \alpha_{\text{o}}\)), występujące w osnowie naprężenia, których składowa styczna do powierzchni wtrąceń jest rozciągająca (\(\sigma_{\theta} > 0\)), powodują, że szczeliny będą odchylane od cząstek *rys. 1.25a). W przypadku odwrotnym, gdy rozszerzalność cieplna wtrąceń jest mniejsza niż osnowy (\(\alpha_{\text{w}}< \alpha_{\text{o}}\)), składowa radialna jest rozciągająca (\(\sigma_r > 0\)), co sprawia, że propagujące szczeliny będą kierowane wprost w kierunku cząstek (rys. 1.25b).
Fluktuacje resztkowych naprężeń cieplnych istotnie wpływają więc na kierunek rozprzestrzeniania się pęknięć i przez to, zgodnie z opisanym już mechanizmem odchylania \eqref{eq:FaberEvansSfer} \eqref{eq:FaberEvansRods} \eqref{eq:FaberEvansDisks}, podnoszą odporność na pękanie. Jednak samo zwiększanie długości szczelin poprzez meandrowanie, prowadzące do wzrostu pola powierzchni spękań rozpraszających energię, nie jest jedynym efektem, który należy uwzględniać przy analizie wpływu RTS na pękanie. Obecne w materiale naprężenia cieplne mogą również zmienić charakter pękania ze wskrośziarnowego na międzyziarnowy i odwrotnie. W efekcie może to prowadzić również do niekorzystnych zmian, wynikających z osłabienia granic międzyziarnowych lub wtrąceń poprzez obniżenie wartości lokalnych, krytycznych szybkości uwalniania energii (\(G_{\text{c}}\)). Zjawiska te zależą jednak nie tylko od właściwości termomechanicznych faz i granic międzyziarnowych, ale również od kształtu, rozmiaru i względnej konfiguracji krystalitów. Dlatego wpływ ten analizowany jest zwykle metodami numerycznymi w oparciu o modelowe albo rzeczywiste mikrostruktury [324, 331, 333, 445, 456, 459, 486–491].
Kolejnym efektem występującym podczas pękania, wynikającym z obecności resztkowych naprężeń cieplnych, jest zaciskanie lub rozwieranie propagujących w materiale szczelin (rys. 1.26). Rozpatrując fluktuacje naprężeń resztkowych w mikroskali \(\sigma^{\text{II}}\) (określanych wcześniej jako naprężenia typu II), wynikających z niedopasowania właściwości termomechanicznych sąsiadujących krystalitów, można zauważyć, że fluktuacje te prowadzą do występowania obszarów, w których naprężenia resztkowe przyjmują wartości dodatnie (naprężenia rozciągające) i obszarów o ujemnych wartościach naprężeń (naprężenia ściskające). Zgodnie z podanym wcześniej warunkiem równowagi mechanicznej \eqref{eq:residual_micro_equil}, naprężenia te, w odpowiednio dużym obszarze, obejmującym swoim zasięgiem populacje wielu krystalitów, równoważą się, jednak lokalnie mogą istotnie wpłynąć na pole naprężeń przy wierzchołku propagującej szczeliny. Jeśli front pęknięcia znajdzie się w strefie, w której dominują ściskające RTS, to dalszy jego rozwój będzie utrudniony. Szczelina będzie zaciskana przez RTS, co w granicznym przypadku może prowadzić do całkowitego wyhamowania procesu pękania. Z drugiej strony, gdy propagacja pęknięć przebiega przez obszary, w których RTS wywołują rozciąganie, to dochodzi wtedy do sprzężenia pomiędzy naprężeniami, które napędza rozwoju szczeliny i w efekcie może prowadzić do wystąpienia katastrofalnego pękania.
Ilościowy opis wpływu pola resztkowych naprężeń cieplnych na pękanie w ceramicznych kompozytach ziarnistych został przedstawiony przez Taya i in. [415]. Rozpatrując kompozyt \(\text{SiC-TiB}_{\text{2}}\), w którym węglikowa osnowa ma mniejszą rozszerzalność cieplną od borkowych wtrąceń (\(\alpha_{\text{o}}< \alpha_{\text{w}}\)), Taya i in. przyjęli, że propagująca w pobliżu wtrąceń szczelina, będzie odchylana zgodnie z mechanizmem opisanym przez Wei i Bechera [485], jednak w obszarze między wtrąceniami (\(\lambda - d\)), wierzchołek pęknięcia będzie poddawany działaniu lokalnego pola RTS o charakterze ściskającym, nakładającego się z polem naprężeń wywołanym zewnętrznym obciążeniem (rys. 1.26). Wartość naprężenia normalnego do powierzchni szczeliny, wywołującego jej zaciskanie, została przybliżona średnim resztkowym naprężeniem cieplnym w osnowie \(\langle \sigma \rangle_{\text{o}}\) \eqref{eq:TayaO}. Przyjmując dodatkowo, że fluktuacje pola RTS są w analizowanym kompozycie periodyczne, wzrost odporności na pękanie wyrazili równaniem wyprowadzonym przez Cutlera i Virkara [492], jako zmianę krytycznego współczynnika intensywności naprężeń daną wyrażeniem [415, 492]: \[\label{eq:Taya_KIC} \Delta K_{\text{Ic}}= - 2 \langle \sigma \rangle_{\text{o}} \sqrt{\frac{2\left( \lambda - d \right)}{\pi}}.\]
Równanie to może być stosowane zarówno do układów, w których \(\alpha_{\text{o}}< \alpha_{\text{w}}\) (jak w kompozycie \(\text{SiC-TiB}_{\text{2}}\)), ale również do szacowania obniżenia odporności na pękanie w kompozytach ziarnistych zawierających wtrącenia o mniejszej rozszerzalności cieplnej niż osnowa. Obliczone w ten sposób wartości zmian \(K_{\text{Ic}}\), wskazują na znaczący udział mechanizmu opartego na efekcie zaciskania w całkowitym umocnieniu. Zjawisko to zostało potwierdzone dla wielu ceramicznych materiałów kompozytowych o osnowach węglikowych [415, 417, 493], borkowych [388, 416, 494, 495], tlenkowych [496–499] i dla materiałów szkło-ceramicznych [424]. Analiza modelu Taya i in. wskazuje również, że przy stałym udziale objętościowym wtrąceń, wzrost umocnienia można osiągnąć poprzez zwiększenie rozmiaru cząstek. Powoduje to wzrost średniej odległości między najbliższymi wtrąceniami (\(\lambda\)) i tym samym zwiększa obszar w którym może zachodzić mechanizm zaciskania [500]. Należy jednak zaznaczyć, że oczekiwane umocnienie, wywołane wzrostem rozmiaru wtrąceń, może niekorzystnie wpłynąć na wytrzymałość, która na ogół maleje wraz ze wzrostem rozmiaru ziaren (por. rozdz. 1.3.2). Prowadzona tą drogą optymalizacja właściwości tworzywa, wiąże się więc zwykle z kompromisem pomiędzy odpornością na pękanie a wytrzymałością.
Bardziej precyzyjny opis wpływu resztkowych naprężeń cieplnych na propagację szczelin, musi jednak ujmować parametry morfologiczne i topologiczne krystalitów (kształt, rozmiar, orientację i wzajemne rozmieszczenie), które w kompozytach ziarnistych wykazują znaczną zmienność. Dlatego analizy takie prowadzone są metodami przybliżonymi w oparciu o syntetyczne bądź rzeczywiste mikrostruktury. Ilustracją mogą być tutaj analizy porównawcze przeprowadzone przez Grabowskiego i in. [170, 201, 501] dla kompozytów \(\text{SiC-TiB}_{\text{2}}\) i \(\text{AlN-TiB}_{\text{2}}\). Symulacje MES, przeprowadzone na dwuwymiarowych modelach opartych na rzeczywistych mikrostrukturach, pozwoliły ustalić, że oprócz różnic w maksymalnych wartościach naprężeń cieplnych występujących między kompozytami, a wynikających bezpośrednio z niedopasowania rozszerzalności cieplnej faz składowych, dochodzi również do zróżnicowania w rozkładzie przestrzennym RTS. Większe niedopasowanie właściwości termomechanicznych występujące w kompozycie \(\text{SiC-TiB}_{\text{2}}\), powoduje tworzenie silnie naprężonych, rozległych stref w węglikowej osnowie, w których dominują naprężenia ściskające mogące skutecznie blokować rozwój pęknięcia. Obszary takie, w osnowie azotkowej drugiego kompozytu (\(\text{AlN-TiB}_{\text{2}}\)), mają tylko lokalny zasięg i przez to efektywność mechanizmu opierającego się na zaciskaniu propagujących szczelin jest w nim mniejsza. Wnioski płynące z przeprowadzonych symulacji, zostały przez autorów skonfrontowane z wynikami analizy fraktograficznej i ostatecznie pozwoliło to tłumaczyć obserwowane różnice w umocnieniu występujące dla analizowanych kompozytów.
Obecność resztkowych naprężeń cieplnych ma również wpływ na mechanizm mostkowania i wyciągania ziaren. Jak już wcześniej wspomniano (zob. p. 1.3.3), RTS nie są konieczne do wystąpienia tych mechanizmów, ale mogą istotnie poprawić ich efektywność. W najprostszym ujęciu, składowa radialna naprężenia cieplnego (\(\sigma_r\)), normalna do powierzchni mostku, podczas wyciągania, wpływa na naprężenie ścinające zgodnie z równaniem \eqref{eq:tarcie_pull}. Korzystny efekt, w postaci wzrostu oporu, uzyskiwany jest oczywiście jedynie w przypadku, gdy mostek jest w stanie naprężeń ściskających i dzięki temu zwiększa wytrzymałości granicy na ścinanie \(\tau_{\text{i}}\). Jednak obecność skumulowanych w mostku naprężeń nie ogranicza się tylko do tego efektu.
Lokalne zmiany naprężenia, występujące podczas rozwierania szczeliny spiętej mostkującym ją ziarnem, można zilustrować modelem przedstawionym przez Bennisona i Lawna [502]. Rozpatrzyli oni kolejno dwa etapy: pierwszy – w którym rozwarcie szczeliny \(u\) jest jeszcze niewielkie i dochodzi do rozwarstwienia granicy międzyziarnowej przy mostkującym ziarnie (rys. 1.27)a, oraz drugi – gdy rozwarcie szczeliny jest na tyle duże (\(u > u_{+}\)), że granica międzyziarnowa zostaje całkowicie rozdzielona i rozpoczyna się proces wyciągania ziarna (rys. 1.27)b.
Naprężenie wywierane na rozwieraną szczelinę przez mostkujące ją ziarno, dla kolejnych etapów, w zależności od rozwarcia \(u\), określone są równaniami [502]: \[\label{eq:BennisonLawn1989Debond} p(u) = p_{\text{d}}\sqrt{\frac{u}{u_{*}}} - \sigma_r \qquad \text{gdy: } 0 \leqslant u < u_{+},\] \[\label{eq:BennisonLawn1989pullout} p(u) = p_{\text{m}}\left(1 - \frac{u}{u_{*}}\right) \qquad \text{gdy: } u_{+} \leqslant u \leqslant u_{*}.\] Stosunek \(u/u_{*}\) określa więc stopień rozwarcia szczeliny; jeśli \(u = u_{*}\), mostek przestaje spinać szczelinę i \(p(u) = 0\). Dodatkowo, wykorzystane w powyższych równaniach parametry skalowania \(p_{\text{d}}\) i \(p_{\text{m}}\) dane są wyrażeniami [502]: \[\label{eq:BennisonLawn1989pD} p_{\text{d}} = \frac{\sqrt{2 \mu \sigma_r E \lambda u_{*}/l^2}} {2d^2/l^2 - 1},\] \[\label{eq:BennisonLawn1989pM} p_{\text{m}} = \mu \sigma_r \lambda u_{*}/d^2 \left( 2d^2/l^2 - 1 \right)\!,\] w których \(\mu\) jest współczynnikiem tarcia dla powierzchni między mostkiem a otaczającymi go ziarnami, \(l\) szerokością mostku, \(\lambda\) długością obwodu mostku (dla wykorzystanych w modelu mostków o przekroju kwadratu \(\lambda = 4l\)), oraz \(d\) odległością między mostkami.
Analiza przedstawionego przez Bennisona i Lawna [502] modelu, pozwala zauważyć, że w pierwszym etapie, kiedy front pęknięcia przejdzie przez mostek, relaksacja skumulowanych w nim naprężeń ściskających, pierwotnie powoduje obniżenie wartości naprężenia zaciskającego szczelinę (\(p(u)\)). Następnie, w miarę wzrostu \(u\), pojawiające się w granicy rozwarstwienie, prowadzi do dalszej relaksacji odkształceń sprężystych i wywołuje niewielki opór związany z tarciem. Opór ten rośnie w miarę wzrostu rozwarstwienia i osiąga wartość maksymalną, gdy cała powierzchnia mostku zostanie oddzielona od otaczających go ziaren (\(u = u_{+}\)). Dalsze rozwieranie szczeliny (\(u \geqslant u_{+}\)) prowadzi do stopniowego wysuwania mostku i zmniejszania powierzchni trącej, co powoduje liniowy spadek naprężenia zaciskającego szczelinę, aż do całkowitego wyciągnięcia mostku, kiedy \(p(u) = 0\).
Przewidywane modelem Bennisona i Lawna [502], zmiany naprężenia zaciskającego szczelinę, zostały przedstawione na rys. 1.27c. Powierzchnia pod krzywą \(p(u)\), odpowiada całkowitej energii rozpraszanej w trakcie procesu mostkowania, poprzez rozwarstwienie i wyciąganie. Dzięki temu model ten może służyć do określenia wielkości umocnienia wywołanego mechanizmem mostkowania, ale jest on użyteczny nie tylko z powodu możliwości ilościowego opisu zjawiska. Wskazuje również, że efekt mostkowania występuje zarówno w klasycznych kompozytach włóknistych, w których powierzchnia zakotwiczenia mostków jest duża, ale również w kompozytach ziarnistych. Przy niewielkiej wartości \(u_{*}\), ograniczonej rozmiarem mostkujących ziaren, decydującą rolę odgrywają resztkowe naprężenia cieplne. Fluktuacje tych naprężeń występujące w kompozytach ziarnistych, ale również w jednofazowych polikryształach ceramicznych, mogą prowadzić do wystąpienia stref, w których wartości naprężeń normalnych do powierzchni granic międzyziarnowych są na tyle duże (niekiedy rzędu GPa), że nawet przy niewielkich wymiarach mostkujących ziaren mogą one skutecznie przeciwdziałać rozwarstwianiu i wyciąganiu poprawiając tym samym efektywność mechanizmu mostkowania. Należy jednak zauważyć, że dla konkretnych materiałów, przewidywania te muszą być uzupełnione o dokładną analizę uwzględniającą opisywane wcześniej czynniki geometryczne wynikające z kształtu, orientacji i rozmieszczenia ziaren (por. p. 1.3.3) oraz o analizę rozkładu naprężeń wewnątrz mostków.
Liczne pomiary i symulacje przeprowadzone metodami przybliżonymi, wskazują, że w izometrycznych ziarnach, ale również w wiskerach, mogących stanowić mostki, rozkład resztkowych naprężeń cieplnych nie jest jednorodny [168, 503, 504]. Anizotropia właściwości termomechanicznych krystalitów, prowadząca do złożonego stanu naprężeń, sprawia więc, że wyniki uzyskiwane na podstawie prostych modeli (zarówno analitycznych jak i numerycznych) nieujmujących tych cech, mogą prowadzić do błędnych wniosków dotyczących możliwości wystąpienia (lub braku) umocnienia w polikryształach.
Ostatnią właściwością, która została już wcześniej poruszona, ale wymaga dodatkowego komentarza, jest wytrzymałość. Wpływ resztkowych naprężeń cieplnych na wytrzymałość polikrystalicznych materiałów ceramicznych 40 można rozpatrywać dla dwóch przypadków. W pierwszym, gdy rozmiar krystalitów \(D\) przekracza wartość graniczną, przy której występuje zjawisko spontanicznego mikropękania (\(D > D_{\text{c}}\)), powstające w materiale szczeliny stają się koncentratorami naprężeń. Sam proces powoduje relaksację RTS i, zgodnie z równaniem Griffitha \eqref{eq:Griffith_PSN}, prowadzi do obniżenia wytrzymałość tworzywa. W przypadku drugim, jeśli rozmiar krystalitów nie przekracza \(D_{\text{c}}\), to istniejące w materiale wady – mogące potencjalnie stać się wadami krytycznymi – będą poddawane działaniu naprężeń resztkowych skumulowanych w materiale. Jednak z uwagi na występujący w polikryształach, złożony stan tych naprężeń, a w szczególności ich fluktuacje, efekt oddziaływania będzie zależał od umiejscowienia wady. W tym samym tworzywie, może więc dochodzić zarówno do zaciskania wad – co w kontekście przywołanej teorii Griffitha, prowadzi do zmniejszania ich promieni i lokalnego wzrostu wytrzymałości, jak i efektu odwrotnego – skutkującego wzrostem promienia wady i obniżeniem wytrzymałości. Jednak zgodnie z regułą najsłabszego ogniwa, na makroskopową wytrzymałość polikryształu, będą miały wpływ głównie zjawiska powodujące powiększanie wad i obniżające lokalną wytrzymałość.
Ilościowo wpływ RTS na wytrzymałość (\(\sigma_{\text{f}}\)) polikrystalicznych tworzyw ceramicznych, można zilustrować równaniem wyprowadzonym przez Krstica [412, 505]: \[\label{eq:KrsticSigmaRTS} \sigma_{\text{f}}= \sqrt{\frac{\pi E \gamma^{*}} {D \left( 1 + 2s/D \right) \left( 1 - \nu \right)^2 } } - A p \varPhi_t,\] w którym: \(s\) określa rozmiar (długość) wady obecnej w materiale; \(A\) jest stałą zależną od poziomu relaksacji naprężeń resztkowych (\(0 \leqslant A \leqslant 1\)); \(p\) wartością naprężenia wywieranego na wadę przez przylegający do niej krystalit, które może zostać przybliżone równaniem Selsinga \eqref{eq:SelsingP}; oraz \(\varPhi_t\) jest współczynnikiem koncentracji naprężeń, zależnym od rozmiaru krystalitu i wady, który może zostać wyznaczony na podstawie równania [412, 506]: \[\label{eq:KrsticPhi} \varPhi_t = 1 - \sqrt{1 - \frac{1}{\left( 1 + 2s/D \right)^2}} + \frac{1}{2\left( 1 + 2s/D \right)^{3/2}} \sqrt{1 - \frac{1}{\left( 1 + 2s/D \right)^2}}.\]
Równane \eqref{eq:KrsticSigmaRTS} pozwala więc na prześledzenie wpływu podstawowych parametrów materiałowych, mikrostrukturalnych oraz resztkowych naprężeń cieplnych na wytrzymałość polikryształu. Można zatem zauważyć (rys. 1.28), że przy małym rozmiarze krystalitów \(D\) (ziarna nanometryczne albo submikronowe) o wytrzymałości decyduje rozmiar wad \(s\) występujących w materiale – wpływ RTS na wytrzymałość jest wtedy niewielki. Jeśli jednak mikrostruktura tworzywa zawiera ziarna mikronowe i większe, to skumulowane w materiale naprężenia cieplne zaczynają odgrywać znaczącą rolę. Można nawet przyjąć, że jeśli rozmiar wad występujących w materiale jest dużo mniejszy od średnicy krystalitów (\(s/D \rightarrow 0\), więc \(\varPhi_t \rightarrow 1\)), co w przypadku ziaren o rozmiarze kilkudziesięciu mikrometrów jest technologicznie zwykle łatwe do osiągnięcia, to resztkowe naprężenia cieplne decydują o wytrzymałości tworzywa.
Przedstawione tutaj wnioski, płynące z analizy modelu Krstica, są w pełni spójne z wcześniej opisaną, empiryczną zależnością między wytrzymałością a rozmiarem krystalitów (por. p. 1.3.2 oraz rys. 1.4). Model ten, uściśla więc opis w zakresie jednofazowych materiałów polikrystalicznych, w których ziarna posiadają strukturę krystaliczną inną niż regularna, oraz ceramicznych kompozytów ziarnistych. Ponieważ w tworzywach tych, obecność resztkowych naprężeń cieplnych w istotny sposób wpływa na wytrzymałość, to aby uzyskać materiały wysokowytrzymałe, należy w procesie technologicznym dążyć do obniżenia zarówno rozmiaru wad, mogących zapoczątkować pękanie, jak również rozmiaru anizotropowych krystalitów, w jednofazowych spiekach czy kompozytowej osnowie, oraz ziaren fazy wtrąconej, generujących resztkowe naprężenia cieplne.
Oprócz fluktuacji RTS występujących lokalnie, których równowaga ustala się w skali mikrometrów – naprężeń typu II (ale też III) – a które, jak to zostało wykazane, wpływają na właściwości materiału, należy również wspomnieć o naprężeniach resztkowych typu I. Naprężenia te – makroskopowe naprężenia własne – kształtowane w procesie technologicznym 41, poprzez prasowanie i obróbkę wykańczającą powierzchni, mogą powodować zmiany właściwości użytkowych wyrobów. W materiałach ceramicznych ich obecność zaznacza się głównie w warstwach powierzchniowych, do kilkudziesięciu mikrometrów [395, 507–510] i, co istotne, dotyczy również materiałów polikrystalicznych o strukturze regularnej. Naprężenia te mogą więc powstawać na skutek mechanicznej obróbki powierzchni, kiedy po spiekaniu wyroby poddawane są szlifowaniu i polerowaniu. W trakcie tych procesów, dochodzi w warstwie przypowierzchniowej do powstawania uszkodzeń: rys, przemieszczeń ziaren i odkształceń plastycznych, wywołanych oddziaływaniem odrabianej powierzchni z cząstkami materiałów ściernych. Powstające rysy, obniżające wytrzymałość, są zwykle usuwane w kolejnych etapach obróbki – w trakcie polerowania, natomiast odkształcenia plastyczne sprawiają, że przy powierzchni kumulują się resztkowe naprężenia ściskające [507, 508, 511–513]. Naprężenia te powodują zaciskanie istniejących w materiale wad i, pod warunkiem, że wady te nie sięgają warstw głębszych, podnoszą wytrzymałość wytwarzanych w ten sposób elementów [92, 139, 512, 513]. W tworzywach zawierających tetragonalną odmianę \(\text{ZrO}_{\text{2}}\), mechaniczna obróbka powierzchniowa może dodatkowo inicjować przemianę martenzytyczną. Efekt ten również prowadzi do wytworzenia stanu naprężeń ściskających w warstwie powierzchniowej i zwiększa wytrzymałość tak wykańczanych elementów [364, 509, 514, 515].
Przedstawione tutaj wybrane efekty występujące w polikrystalicznych materiałach ceramicznych, a wynikające z obecności w nich naprężeń resztkowych, wskazują, że wpływ tych naprężeń na właściwości tworzyw jest złożony. Wynika to z różnych źródeł powstawania RS, które zostały zebrane już wcześniej na rysunku 1.12. Wartość naprężeń i ich rozkład w próbce czy, w ujęciu technicznym, elemencie, jest więc sumą wszystkich czynników (fizycznych i chemicznych), które oddziałują aktualnie, jak i tych, które wystąpiły wcześniej, podczas całego procesu technologicznego prowadzącego do uzyskania gotowego wyrobu. Odtworzenie historii tworzywa, która ukształtowała jego mikrostrukturę i wprowadziła do niego naprężenia resztkowe, w postaci modeli obliczeniowych może zatem pozwolić na bardzo precyzyjne przewidywanie jego właściwości i niezawodności [177, 346, 388, 516].
Spontaniczne mikropękanie jednofazowych polikryształów ceramicznych, obserwowane jest jedynie w materiałach wykazujących anizotropię rozszerzalności cieplnej krystalitów. Zjawisko to nie występuje w materiałach o strukturze regularnej.↩︎
Dotyczy to wyłącznie polikryształów, których krystality nie posiadają struktury regularnej i występują w nich RTS, wynikające z anizotropii właściwości termomechanicznych.↩︎
Dlatego naprężenia takie nazywane są także naprężeniami technologicznymi.↩︎
Opisane w tym rozdziale właściwości polikrystalicznych tworzyw ceramicznych oraz ich związki z cechami mikrostruktury, stanowią jedynie niewielki fragment obszaru zainteresowań inżynierii materiałowej. Jednak nawet w przypadku ograniczenia rozważań do tych cech, które są najbardziej podstawowe dla tworzyw konstrukcyjnych, można zauważyć, że trudny, a zwykle wręcz niemożliwy, jest precyzyjny opis, wybranych właściwości czy związków, bez uwzględnienia wpływu pozostałych parametrów materiałowych. Ujmując to inaczej – makroskopowe właściwości materiałów i ich mikrostruktura są wzajemnie sprzężone. Najczęściej nie jest więc możliwa prosta optymalizacja właściwości poprzez modyfikację tylko jednego parametru: rozmiaru czy kształtu ziaren, dodatku innej fazy, porowatości czy składu granic międzyziarnowych, ponieważ powoduje to zmianę pozostałych parametrów. Stąd wynikają trudności technologiczne, występujące podczas modyfikacji istniejących już tworzyw, ale również komplikacje interpretacyjne, pojawiające się podczas badań podstawowych.
Modele analityczne, które zostały wybrane do zilustrowania najważniejszych zależności występujących w rozpatrywanych materiałach, były przedmiotem badań przez wiele dziesięcioleci i w latach 90., osiągnęły poziom pozwalający na wystarczająco dokładny opis właściwości wielu tworzyw ceramicznych, a nawet, w niektórych aspektach, uzyskały zdolność predykcyjną. Tym samym, modele te spełniły ważną rolę w rozwoju inżynierii materiałowej, przyczyniając się do postępu jaki dokonał się pod koniec XX wieku w technologii materiałów ceramicznych: w zakresie optymalizacji istniejących tworzyw i otrzymywania nowych materiałów konstrukcyjnych, spełniających rosnące wymagania stawiane przez przemysł i nowe technologie.
Jednak rozwój metod badawczych, w tym również technik obrazowania, oraz rosnąca ilość danych pomiarowych, które stały się dostępne dla szerokiej grupy specjalistów z różnych dziedzin, pozwoliła na badanie coraz bardziej szczegółowych efektów występujących zarówno w materiałach ceramicznych, ale również metalicznych, polimerowych i kompozytowych. Zastosowanie modeli stochastycznych, oraz coraz większa komplikacja klasycznych modeli analitycznych, wymusiła zastosowanie metod numerycznych, które na przełomie stuleci stały się szeroko wykorzystywanym narzędziem w nauce o materiałach. W ostatnim dwudziestoleciu, związki pomiędzy mikrostrukturą a właściwościami materiałów są coraz częściej analizowane metodami przybliżonymi, w oparciu o dane pozwalające na rekonstrukcję budowy materiałów w skali mikrometrów – na poziomie pojedynczych krystalitów – a nawet uwzględniające niejednorodności w skali nanometrów. Zastosowanie metod dynamiki molekularnej, jeszcze bardziej przesuwa tę granicę, w obszar pozwalający na uwzględnienie oddziaływań na poziomie atomowym.
Tak duże poszerzenie zakresu rozważanych zjawisk i uszczegółowienie prowadzonych analiz, okupione jest jednak niespotykanym do tej pory przyrostem ilości informacji, które muszą być przetwarzane w celu uzyskania odpowiedzi na stawiane pytania badawcze. Dlatego aktualnie w inżynierii materiałowej, obok fizyki czy chemii, niezbędna staje się wiedza z zakresu informatyki i statystycznej analizy danych. W tak poszerzonym obszarze badawczym, coraz częściej pojawiają się więc nowe dyscypliny: informatyka materiałowa i data science, łączące kompetencje z zakresu matematyki, statystyki, bazy danych i programowania z wiedzą o budowie i właściwościach materiałów. Połączenie wielu metod, opracowanych niezależnie w każdej z tych dziedzin, umożliwia uzyskanie niezwykle dokładnego opisu właściwości, poprzez wykorzystanie zbiorów danych pomiarowych uzyskanych precyzyjnymi technikami pomiarowymi. Ale przede wszystkim, daje nadzieję na dogłębniejsze poznanie przyczyn wielu zjawisk, co może zostać osiągnięte w oparciu o analizę szczegółowo opisanej budowy wewnętrznej materiałów. Opis metod, pozwalających na pozyskiwanie takich informacji, zawarty został w kolejnym rozdziale.
Powszechnie stosowana metoda w technologii materiałowej (ceramicznej, metalurgicznej, polimerowej czy chemicznej), służąca poprawie właściwości znanych już tworzyw, ale również stosowana podczas otrzymywania nowych materiałów, opiera się na cyklicznym prowadzaniu prób laboratoryjnych i stopniowej modyfikacji składu i parametrów syntezy. Kolejne zmiany, dokonywane w trakcie serii badań, opierają się na analizie uzyskanych wyników kontrolnych. Ustalone w ten sposób związki między istotnymi czynnikami decydującymi o właściwościach tworzywa, ale również wcześniej zdobyta wiedza i doświadczenie dla podobnych materiałów, a niekiedy wręcz intuicja, wykorzystywane są do dalszej modyfikacji parametrów wejściowych procesu i kolejnych powtórzeń cyklu badań. Metoda ta, pomimo jej dużej użyteczności i skuteczności, jest jednak kosztowna i czasochłonna. Aby więc skrócić taki cykl, niezbędne jest poznanie, opisanie a następnie wykorzystanie, fundamentalnych praw rządzących oddziaływaniami w różnych skalach.
W takim wieloskalowym ujęciu, mikrostruktura jest ogniwem pośrednim, łączącym oddziaływania na poziomie atomowym z makroskopowymi właściwościami materiałów. Jej uwzględnienie w opisie jest zwykle niezbędne, ponieważ praktycznie wszystkie materiały naturalne i syntetyczne, oprócz monokryształów i materiałów amorficznych (np. szkieł czy niektórych polimerów), posiadają heterogeniczną budowę wewnętrzną. W materiałach jednofazowych obecne są granice pomiędzy krystalitami o różnej orientacji przestrzennej, a w materiałach wielofazowych, granice pomiędzy fazami. Mogą one występować zarówno między fazami stałymi, stałymi i ciekłymi oraz stanowić powierzchnie swobodne w tworzywach porowatych. Elementy materiału wydzielone takimi granicami, będą zatem posiadać swoisty kształt, rozmiar, orientację i jednorodne bądź zmienne (o ustalonym gradiencie) właściwości. Z jednej strony, wszystkie te cechy są związane ze strukturą na poziomie atomowym, a z drugiej – mają znaczący wpływ na makroskopowe właściwości materiałów, co stanowi jeden z paradygmatów inżynierii materiałowej.
Ilościowy opis parametrów morfologicznych, krystalograficznych i topologicznych mikrostruktury, ma więc istotne znaczenie zarówno w kontekście badań podstawowych jak i w aspekcie praktycznym (inżynierskim i technologicznym). Wspomagane komputerowo projektowanie i optymalizacja tworzyw, opierające się na symulacjach pozwalających zastępować, albo przynajmniej ograniczać, zakres badań laboratoryjnych, wymagają coraz wierniejszego odwzorowania rzeczywistej budowy materiałów. Dokładność aktualnie stosowanych w inżynierii materiałowej modeli numerycznych, a co za tym idzie, ich zdolność do przewidywania właściwości, zależy nie tylko od zaimplementowanych w nich praw fizycznych (związków konstytutywnych) czy od precyzyjnego odtworzenia stanu obciążeń zewnętrznych, ale również od jakości opisu mikrostruktury.
Klasyczne metody reprezentacji mikrostruktury stosowane w modelach analitycznych, opierające się na dwuwymiarowej geometrii, w której kształt elementów budowy był przybliżany prostymi figurami (kołami, równoległobokami), ale też uproszczonych modeli trójwymiarowych, zawierających kule i prostopadłościany, są niewystarczające do osiągnięcia wymaganej precyzji. Takie uproszczenia, daleko odbiegają od rzeczywistej morfologii krystalitów i przez to pomijają albo zniekształcają lokalne oddziaływania, które mają istotny wpływ na makroskopowy opis właściwości materiałów. Dlatego w tym rozdziale omówione zostaną metody doświadczalne i obliczeniowe, pozwalające na cyfrową rekonstrukcję wewnętrznej budowy materiałów polikrystalicznych, mogącą służyć do formułowania zaawansowanych modeli numerycznych.
Cyfrowa, trójwymiarowa (3D) rekonstrukcja mikrostruktury jest naturalnym kierunkiem rozwoju metod doskonalonych przez stulecia, służących do opisu budowy wewnętrznej materiałów. Główna trudność w poznaniu wnętrza polikryształów, wynikała początkowo z samej natury oddziaływania promieniowania elektromagnetycznego z materią. W zakresie widzialnym, promieniowanie to jest intensywnie pochłaniane i rozpraszane przez polikryształy, co sprawia, że większość materiałów konstrukcyjnych jest praktycznie nieprzeźroczysta. Początki badań budowy materiałów, dotyczyły więc jedynie analizy powierzchni przełomów czy później, w miarę rozwoju technik badawczych, płaskich przekrojów. Dla potrzeb takich analiz, stworzona została stereologia, która pozwala wnioskować o budowie wewnętrznej na podstawie obserwacji wykonanych na dwuwymiarowych (2D) przekrojach, i która z czasem rozwinęła się w niezależną dziedzinę matematyki [517, 518]. Ustalone związki stereologiczne między parametrami w różnych wymiarach przestrzennych oraz specyficzna notacja przyjęta do opisu tych parametrów, pozwalają na zwięzły, ilościowy opis mikrostruktury. Co prawda, współczesne metody pozyskiwania informacji o budowie wewnętrznej materiałów, dają możliwość cyfrowej, trójwymiarowej rekonstrukcji mikrostruktury, jednak znajomość prostych i eleganckich technik stereologicznych, sprawia, że korzystanie z zaawansowanych, czasochłonnych i kosztownych technik 3D jest w niektórych zastosowaniach niepraktyczne lub wręcz nieuzasadnione. Warto również zaznaczyć, że płaskie przekroje mogą być rejestrowane ze znacznie większą precyzją niż jest to możliwe w przypadku bezpośrednich technik 3D, przez co niekiedy, jedynym sposobem na uzyskanie informacji o trójwymiarowych obiektach może być badanie ich dwuwymiarowych przekrojów [237]. Dlatego we wstępie do metod rekonstrukcyjnych, zostaną wprowadzone najważniejsze pojęcia stereologiczne i określone granice stosowalności metod klasycznych.
Podstawowymi elementami mikrostruktury [519, 520], obecnymi w polikrystalicznych tworzywach ceramicznych, są zarówno obiekty trójwymiarowe (3D) – posiadające objętość – takie jak: cząstki czy pory, jak również obiekty dwuwymiarowe (2D) – posiadające powierzchnię – stanowiące granice między elementami trójwymiarowymi, albo będące obiektami, których jeden z wymiarów jest dużo mniejszy w porównaniu do pozostałych. Przykładem obiektów 2D mogą być granice międzyziarnowe czy dyslokacje. Krzywe powstałe z przecięcia obiektów dwuwymiarowych, albo będące krawędziami obiektów trójwymiarowych (praktycznie charakteryzujące się jedynie długością), zaliczane są do obiektów jednowymiarowych (1D). Ostatnią kategorię obiektów stanowią elementy punktowe (zero-wymiarowe – 0D), których przykładem mogą być punkty potrójne, obserwowane na przekrojach (zgładach metalograficznych) w miejscu przecięcia granic międzyziarnowych albo obiekty o znikomo małych wymiarach.
Parametry opisujące geometryczne cechy wymienionych elementów mikrostruktury, można podzielić na metryczne i topologiczne [517, 519]. Parametry metryczne, opisują objętość, pole powierzchni, długość oraz krzywiznę i wyrażane są najczęściej jako wielkości względne, w odniesieniu do jednostkowej miary danej przestrzeni: objętości próbki \(V\), jej powierzchni \(A\) czy długości \(L\). Podczas analizy obrazu mikrostruktury stosowane są również odniesienia do punktów (pikseli) obrazu \(P\). Korzystając zatem z notacji stereologicznej, kolejne parametry metryczne można wyrazić jako: \(V_V\) czyli objętość cząstek przypadająca na jednostkę objętości próbki (a więc udział objętościowy cząstek czy fazy), \(S_V\) powierzchnię elementów 2D przypadającą na jednostkę objętości i tak dalej. Z kolei parametry topologiczne, określane są poprzez zliczanie i wyrażane również względem jednostkowej objętości, powierzchni czy długości. Tak więc \(N_V\) oznacza liczbę elementów (np. cząstek) przypadającą na jednostkę objętości, a \(N_A\) jest parametrem topologicznym odniesionym do powierzchni próbki.
Parametry opisujące cechy w odniesieniu do określonej miary danej przestrzeni są nazywane również parametrami globalnymi (integralnymi). Określają bowiem liczbowo cechy całej zbiorowość elementów występujących w rozpatrywanej przestrzeni (badanej próbce). Na ich podstawie można również wyznaczyć parametry statystyczne (lokalne) charakteryzujące uśrednione wartości dla elementów mikrostruktury. Przykładowo, średnia objętość cząstki może zostać wyrażona jako: \(\langle V \rangle= V_V/N_V\), a średnia powierzchnia \(\langle S \rangle = S_V/N_V\). W oparciu o wartości odchylenia standardowego dla objętości \(\sigma_V\) i powierzchni \(\sigma_A\), można również wyznaczyć odpowiednie współczynniki zmienności: \(\sigma_V /\langle V \rangle\) oraz \(\sigma_A /\langle A \rangle\), które są miarami rozrzutu mierzonych parametrów [518, 519].
Ponieważ analiza mikrostruktury rozwinęła się w oparciu o wyniki pomiarów uzyskiwanych dla dwuwymiarowych przekrojów, istotne są związki stereologiczne, które pozwalają przejść z jednej przestrzeni wymiarowej do innej. Badając więc parametry mikrostruktury na płaszczyźnie 42 : metodą planimetryczną (\(S_A\), \(N_A\)), metodą liniową (\(L_L\), \(N_L\)), czy punktową (\(P_P\)) – ostatecznie, ważne jest ustalenie wartości tych parametrów w odniesieniu do objętości – w przestrzeni trójwymiarowej. Takiej transformacji można jednak dokonać tylko dla wybranych cech mikrostruktury.
Dla klasycznych technik stereologicznych, opierających się na pomiarach prowadzonych na losowych, dwuwymiarowych przekrojach (zgładach metalograficznych), DeHoff [522] wprowadził podział parametrów mikrostruktury. Podział ten (przedstawiony w tabeli [tab:DeHoffMikrosParam]), wykorzystuje możliwość estymacji parametrów na podstawie pomiarów dokonywanych na płaszczyźnie. W pierwszej klasie znajdują się zatem parametry mikrostruktury, które mogą zostać określone bez żadnych dodatkowych założeń geometrycznych dotyczących budowy materiału. Są wśród nich: udział objętościowy \(V_V\), który jest wyznaczany bezpośrednio z udziału powierzchniowego na podstawie zależności Cavalieri–Hacquerta (\(V_V = S_A = P_P\)), powierzchnia elementów dwuwymiarowych odniesiona do jednostkowej objętości \(S_V\), którą można ustalić na podstawie pomiarów metodą liniową (\(S_V = 2 P_L\)) i długość elementów liniowych odniesiona do jednostki objętości \(L_V\), która związana jest z liczbą przecięć, przypadającą na jednostkę powierzchni (\(L_V = 2 N_A\)). Oprócz tych parametrów, na podstawie pomiarów dokonywanych na zgładach, można również wyznaczyć parametry opisujące krzywizną elementów powierzchniowych i liniowych. Wyznaczenie tych parametrów nie wymaga więc stosowania zaawansowanych metod pomiarowych i obliczeniowych, a pozwala na uzyskanie szeregu przydatnych informacji o mikrostrukturze badanego tworzywa.
Parametry te nie wystarczają jednak do pełnego opisu budowy wewnętrznej materiału. Przede wszystkim brakuje wśród nich takich, które określają cechy geometryczne elementów trójwymiarowych. Oprócz udziału objętościowego (\(V_V\)), powinny one również charakteryzować kształt, rozmiar, rozkład przestrzenny, ułożenie względem sąsiadujących elementów i orientację przestrzenną cząstek, ziaren, porów czy krystalitów [523]. Informacje takie są niezbędne do szczegółowej analizy mikrostruktury, a w szczególności do cyfrowej rekonstrukcji budowy wewnętrznej materiału.
Niektóre z wymienionych cech, można jednak estymować na podstawie parametrów uzyskanych na podstawie klasycznych pomiarów (2D). Muszą one być jednak ustalane w oparciu o założenia geometryczne dotyczące kształtu cząstek. Takie parametry zaliczane są do klasy II. Ważnym parametrem w tej klasie jest choćby liczba cząstek w jednostkowej objętości (\(N_V\)). Bez przyjęcia założenia dotyczącego kształtu cząstek, albo przynajmniej ich wypukłości, wyznaczenie tego podstawowego parametru jest niemożliwe [517, 518, 522, 524]. Jednak największym ograniczeniem klasycznych metod stereologicznych jest brak możliwości ustalenia rzeczywistego kształtu cząstek. Parametry mogące opisywać tę cechę należą do III klasy, a zatem na podstawie pomiarów prowadzonych na dwuwymiarowych przekrojach nie jest możliwe ich określenie [517, 522].
Ograniczenia klasycznych metod stereologicznych mogą być częściowo złagodzone przez zastosowanie metody disektora [525]. Metoda ta polega na analizie parametrów pochodzących ze sprzężonych ze sobą, równoległych przekrojów badanej próbki i pozwala na dokładne wyznaczenie liczby cząstek przypadających na jednostkową objętość (\(N_V\)), bez dodatkowych założeń geometrycznych dotyczących ich kształtu, rozmiaru oraz orientacji. Kluczowym parametrem w tej metodzie i metodach pokrewnych 43, jest odległość między analizowanymi płaszczyznami. Powinna ona być mniejsza niż wysokość najmniejszej cząstki w kierunku prostopadłym do płaszczyzn przekroju. Dla materiałów inżynierskich utrzymanie reżimu stałej i niewielkiej odległości między kolejnymi przekrojami w połączeniu ze stosunkowo dużym obszarem analizy, zapewniającym reprezentatywność, wymaga zastosowania zaawansowanych technik laboratoryjnych. Zapewnienie jednak warunków niezbędnych do przeprowadzenia pomiarów metodą disektora, pozwala już łatwo rozszerzyć zakres badań o kolejne przekroje i tym samym przejść do technik analizy mikrostruktury opierających się na trójwymiarowych cyfrowych rekonstrukcjach (zob. metoda przekrojów seryjnych p. 2.5.2).
Należy jednak zaznaczyć, że fundamentalne związki stereologiczne, służące do szacowania parametrów mikrostruktury w przestrzeni trójwymiarowej, zarówno na podstawie klasycznych pomiarów wykonywanych na losowych zgładach, jak i metodami wykorzystującymi założenia disektora, pozwalają na dokładne określenie podstawowych parametrów ilościowych opisujących budowę wewnętrzną materiału. Podstawowe równania stereologiczne nie są jedynie przybliżeniami, ale stanowią ścisłe relacje matematyczne. Najważniejsze związki stereologiczne zostały zebrane w tabeli [tab:2_2].
Opis klasycznych metod analizy mikrostruktury, opierających się na pomiarach przeprowadzanych dla zgładów metalograficznych, wykracza poza ramy tego opracowania, a szczegółowe informacje dotyczące stosowanych technik zawarte są w wielu książkach z zakresu stereologii i analizy obrazu [517, 519–521].↩︎
Metoda disektora stała się podstawą dla kilku innych metod opartych na tych samych założeniach teoretycznych (selektora [526], frakcjonatora i nukleatora [527, 528], orientatora i trisektora [529]), jednak zasadniczo różniących się sposobem implementacji nieobciążonych estymatorów dla opisywanych parametrów mikrostruktury [520, 530, 531].↩︎
Jedną z najważniejszych cech mikrostruktury jest kształt cząstek. W kontekście analizy obrazu, wykorzystywanej do badania budowy wewnętrznej materiału, cząstkami mogą być zarówno pojedyncze krystality w polikryształach, jak i ziarna czy włókna fazy wtrąconej w materiałach kompozytowych. Także pory obecne w tworzywach ceramicznych, mogą być traktowane jak szczególny przypadek cząstek; podczas analizy obrazu i w matematycznym opisie kształtu nie ma między nimi żadnej istotnej różnicy. Kształt cząstek, jest więc cechą, na którą wpływają praktycznie wszystkie etapy technologiczne: począwszy od syntezy substratów, otrzymywania proszków, formowania, jak i spiekania. Dlatego ostateczna forma, jaką przybierają cząstki w litym tworzywie, niesie informacje o całym procesie otrzymywania i przez to może zostać wykorzystana do jego analizy. W takim kontekście, rozpoznanie charakterystycznego kształtu elementów mikrostruktury, może pozwolić na ich wstępną klasyfikację z uwagi na źródło pochodzenia czy nawet skład fazowy. Ale przede wszystkim, kształt cząstek istotnie wpływa na właściwości tworzywa i dlatego musi zostać uwzględniony w cyfrowych rekonstrukcjach służących do analiz prowadzonych metodami przybliżonymi.
Kształt, jest pojęciem niezależnym od rozmiaru ciała i jego orientacji [517, 532]. Dlatego można go opisywać bezwymiarowymi parametrami, określającymi liczbę krawędzi, boków, wierzchołków, podającymi stosunki długości, powierzchni czy objętości, ale również kątami między płaszczyznami czy parametrami opisującymi krzywiznę oraz pofałdowanie powierzchni. Jednak tylko dla prostych figur do pełnego opisu kształtu wystarcza jeden bądź kilka takich parametrów. W ogólnym przypadku ich liczba jest nieskończenie wielka [518]. W praktyce, do opisu kształtu cząstek, wykorzystywany jest ograniczony zestaw parametrów, a ich kształt przybliżany jest z kształtem wzorców: kul, elipsoid, prętów, cylindrów, dysków, graniastosłupów, ośmiościanów ściętych i dwunastościanów.
Dla cząstek wypukłych, często stosowanym wzorcem kształtu jest kula. Stopień odstępstwa od kształtu wzorca określany jest bezwymiarowymi współczynnikami kształtu. Przykładowo, jednym z takich współczynników jest stosunek objętości cząstki do jej powierzchni, które są podniesione do odpowiednich potęg, tak aby uzyskany iloraz był bezwymiarowy: \(f_k = V^{1/3}/S^{1/2}\). Dla kuli, współczynnik ten przyjmuje maksymalną wartość \(f_k =\)0.4547, a dla cząstek, których kształt odbiega od kulistego, wartość \(f_k\) będzie mniejsza. W przypadku analizy prowadzonej na podstawie obrazów mikrostruktury, kształt dwuwymiarowych cząstek obecnych na obrazie jest porównywany do koła a odstępstwo określane jest współczynnikiem kolistości 44 (ang. circularity). Jest on wyrażony stosunkiem pola powierzchni cząstki do kwadratu jej obwodu \(f_c = 4\pi\left(S/L^2\right)\) i dla koła przyjmuje wartość 1, a dla cząstek o innych kształtach \(f_c < 1\). Odwrotność tego współczynnika stosowana jest również do opisu pofałdowania powierzchni.
W przypadku cząstek, których kształt znacząco odbiega od kształtu kuli (np. włókien) istotnym parametrem kształtu jest współczynnik wydłużenia (ang. elongation), który dany jest stosunkiem długości cząstki do jej szerokości (\(f_e = L_a/L_b\)).
Krystality budujące jednofazowe materiały polikrystaliczne, mogą być również porównywane do wielościanów, których kształt zapewnia minimum energii swobodnej. Warunek minimum energii osiągany jest, gdy cząstki posiadają najmniejszą powierzchnię granic przy określonej objętości i dodatkowo, kiedy całkowicie wypełniają przestrzeń [517]. W układzie monodyspersyjnym, w którym wszystkie wielościany mają jednakową objętość, minimum energii zapewnia tetrakaidekaedr – czternastościan Kelvina [16] (rys. 2.1). Wielościan ten jest uważany za model idealnego ziarna 45. Posiada on 6 ścian o kształcie kwadratu i 8 ścian o kształcie sześciokąta foremnego, które tworzą 36 krawędzi i 24 wierzchołki, a średnia wartość kątów między ścianami wynosi 120 ° (\(\sim\)109.47 ° między ścianami sześciokątnymi i \(\sim\)125.26 ° między ścianami sześciokątnymi a kwadratowymi). Parametry geometryczne tetrakaidekaedru mogą zatem stanowić wskaźniki będące miarą odstępstwa analizowanej struktury od wzorca.
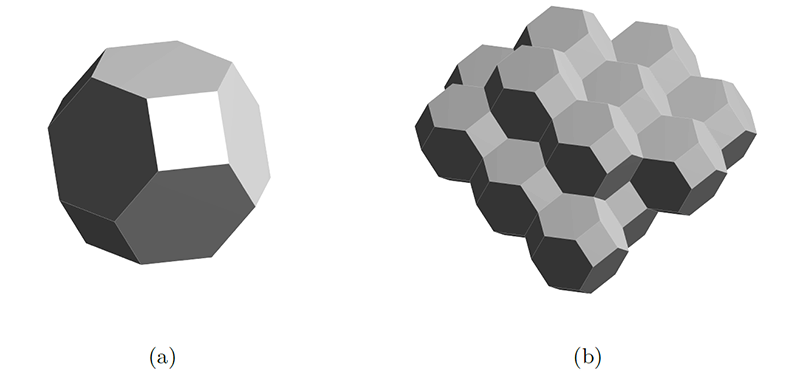
W praktyce stosowanych jest wiele różnych współczynników kształtu. Ich nomenklatura nie jest jednak ujednolicona i dlatego istotne jest odwoływanie się do ścisłego, matematycznego opisu tych współczynników.↩︎
Weaire i Phelan [533] na podstawie przeprowadzonych symulacji komputerowych, uzyskali strukturę o nieco niższej energii od struktury Kelvina [16]. Składa się ona jednak z dwóch rodzajów wielościanów o jednakowej objętości: nieregularnego dwunastościanu o ścianach pięciokątnych i czternastościanu o dwóch ścianach sześciokątnych i dwunastu pięciokątnych.↩︎
Z uwagi na zróżnicowane kształty cząstek, które – jak było to już wcześniej wspomniane – w przypadku polikryształów ceramicznych, mogą być krystalitami, ziarnami wtrąceń czy porami, uniwersalnym parametrem określającym rozmiar jest objętość. Przy zastosowaniu metod wykorzystujących dwuwymiarowe przekroje (obrazy mikrostruktury), bezpośredni pomiar objętości nie jest oczywiście możliwy 46. Dlatego określana jest zwykle średnia objętość cząstek \(\langle V \rangle\), która może zostać estymowana w oparciu o koncepcję disektora, długości siecznych dla punktowo próbkowanych przekrojów (PSI, ang. point sampled intercepts) czy metody opierające się na założeniach geometrycznych odnośnie kształtu mierzonych cząstek [520, 534, 535].
Estymacja \(\langle V \rangle\) metodą disektora, polega na bezpośrednim wyznaczeniu wartości \(N_V\) (zob. tab. [tab:2_2]), która z kolei związana jest ze średnią objętością cząstek w rozpatrywanej objętości zależnością \(\langle V \rangle= 1/N_V\). Jednak pomimo prostej zależności pozwalającej na dokładne wyznaczenie \(\langle V \rangle\), opisywane już trudności techniczne sprawiają, że w inżynierii materiałowej częściej wykorzystywane są pozostałe dwie metody.
Metoda PSI, zaproponowana przez Gundersena i Jensena [528, 536], opiera się na pomiarze długości siecznych przecinających cząstki (\(l_0\)), poprowadzonych z losowo wybranych punktów na obrazie mikrostruktury. Na podstawie pomiarów przeprowadzonych dla \(n\) punktów i związanych z nimi siecznych, objętościowo ważoną średnią objętość cząstek \(\langle V \rangle_{\scriptscriptstyle V}\) można wyrazić zależnością [528, 536]: \[\label{eq:PSI_Vavg} \langle V \rangle_{\scriptscriptstyle V} = \frac{\pi}{3} \langle l_0^3 \rangle = \frac{\pi}{3n} \sum\limits_{i=1}^{n} l_{0,i}^3\]
W metodzie tej nie są wykorzystywane dodatkowe założenia geometryczne, jednak systematycznie przeszacowuje ona wartość \(\langle V \rangle\) [530, 535]. Różnica pomiędzy wartością prawdziwą a estymowaną metodą PSI, jest tym większa im wyższy jest stopień niejednorodności wielkości cząstek.
Metody pośrednie, opierają się na założeniach geometrycznych dotyczących kształtu cząstek. Wykorzystywana jest w nich fundamentalna zależność stereologiczna, oparta na prawdopodobieństwie geometrycznym, przecięcia wypukłej cząstki zawartej w pewnej objętości płaszczyzną czy prostą. Zależność ta pozwala powiązać liczbę cząstek zliczonych na powierzchni przekroju (\(N_A\), ale również na prostej \(N_L\)) z liczbą cząstek zawartych w objętości (\(N_V\)). Dla polidyspersyjnego układu wypukłych cząstek, przypadkowo rozmieszczonych i zorientowanych w przestrzeni można zapisać że [537]: \[\label{eq:stereoNaNv} N_A = N_V \langle H' \rangle,\] przy czym \(\langle H' \rangle\) jest średnią wysokością losowo zorientowanej cząstki w kierunku prostopadłym do płaszczyzny testowego przekroju (zgładu). Dla obiektów o prostych kształtach \(\langle H' \rangle\) może zostać analitycznie wyznaczona poprzez uśrednienie wysokości po wszystkich możliwych rotacjach określonych kątami \(\phi\) i \(\theta\) [517]: \[\label{eq:Havg} \langle H' \rangle = \int\limits_{0}^{2\pi}\int\limits_{0}^{\pi} H'(\phi, \theta)\frac{\sin \theta}{4\pi}\mathop{}\!\mathrm{d}\phi \mathop{}\!\mathrm{d}\theta.\]
Na podstawie powyższego równania zostały wyznaczone zależności łączące \(\langle H' \rangle\) z parametrami opisującymi wymiary charakterystyczne dla wielu prostych brył wypukłych w układach monodyspersyjnych (dla cząstek o jednakowych rozmiarach) [517, 537]. W układach polidyspersyjnych, którymi są typowe polikryształy ceramiczne, wykorzystywane są najczęściej rozwiązania oparte na kształcie kulistym. W takim przypadku średnica kulistej cząstki \(D\) jest równa wysokości cząstki \(H'\), a w układzie polidyspersyjnym średnia średnica kulistych cząstek \(\langle D \rangle\) będzie odpowiadać \(\langle H' \rangle\). Zatem równanie \eqref{eq:stereoNaNv} można przekształcić do postaci [517]: \[\label{eq:D_NaNv} \langle D \rangle = \frac{N_A}{N_V}.\]
Do ustalenia średniej średnicy cząstek niezbędne jest więc wyznaczenie zarówno \(N_A\) jak i \(N_V\). O ile wyznaczenie \(N_A\) nie stanowi trudności, to dokładne wyznaczenie \(N_V\) na podstawie losowych przekrojów nie jest możliwe. Dlatego do oszacowania wartości \(N_V\) może zostać zastosowana przybliżona metoda odwrotności średnic Sałtykowa [538], którą można sprowadzić do zależności \(N_V = \frac{2}{\pi}\langle \frac{1}{d} \rangle N_A\). W równaniu tym, \(\langle \frac{1}{d} \rangle\) oznacza średnią z odwrotności średnic cząstek \(d\) wyznaczonych na podstawie pomiarów przeprowadzonych na płaskich przekrojach (zgładach metalograficznych). Ostatecznie, po podstawieniu tak wyznaczonego \(N_V\) do równania \eqref{eq:D_NaNv}, można wyznaczyć średnią średnicę cząstek [517]: \[\label{eq:D_Saltykov} \langle D \rangle = \frac{N_A}{N_V} = \frac{\pi}{2}\left\langle \frac{1}{d} \right\rangle^{\!-1}\!\!.\]
W tego typu oszacowaniach, w zależności od przyjętego wzorca dla kształtu, wartość współczynnika korekcyjnego oraz postać równań wiążących wymiary cząstek widocznych na przekrojach z rozmiarem odpowiadających im ziaren w trzech wymiarach, są różne [535, 539]. Jednak niezależnie od przyjętej formy równania, wynikającej z zastosowanego wzorca kształtu, z równań tych jednoznacznie wynika, że średni rozmiar cząstek wyznaczony na podstawie (dwuwymiarowych) obrazów mikrostruktury, nie jest równy średniemu rozmiarowi rzeczywistych (trójwymiarowych) ziaren obecnych w materiale.
W praktyce, do ilościowego opisu mikrostruktury, wykorzystywane są również inne miary pozwalające na określenie rozmiaru cząstek. Podczas analizy obrazu (2D), oprócz średnicy \(d\), która, z uwagi na niekolisty kształt cząstek, zwykle odpowiada średnicy równoważnej obliczanej na podstawie pola powierzchni cząstki (\(d = \sqrt{4S/\pi}\)), wykorzystywane są liniowe parametry określające wymiary cząstek. Przykładem takich parametrów mogą być średnice Fereta. Wyrażają one odległość pomiędzy dwoma równoległymi prostymi (a w przypadku 3D – płaszczyznami), które ograniczają mierzoną cząstkę w kierunku prostopadłym do tych prostych i w zależności od kierunku pomiaru mogą przyjmować różne wartości. Parametry te zostały przedstawione na rysunku 2.2.
Dla cząstek izometrycznych często stosowanym parametrem opisującym ich rozmiar jest średnia cięciwa \(\langle L \rangle\), która określa odległość pomiędzy granicami cząstki wzdłuż siecznych i dana jest podstawową zależnością stereologiczną: \(\langle L \rangle = L_L/N_L\), która dla struktur jednofazowych upraszcza się do wyrażenia: \(\langle L \rangle = 1/N_L = 1/P_L\). Pozwala to na szybkie oszacowanie rozmiaru cząstek, a z uwagi na relację \(S_V = 2P_L\) (zob. tab. [tab:2_2]) uważana jest za dobry estymator rozmiaru ziarna w 3D [517].
W układach wielofazowych istotnym parametrem mikrostruktury jest średnia odległość swobodna (MFD, ang. Mean Free Distance) między cząstkami \(\lambda\). Dla wybranej fazy, o udziale objętościowym \((V_V)_\alpha\), można wyrazić ją zależnością [191, 537]: \[\label{eq:MeanFreeDistance} \lambda = \frac{1 - (V_V)_\alpha}{N_L},\] w której \(N_L\) jest liczbą cząstek (analizowanej fazy) przypadająca na jednostkową długość.
Średnia odległość swobodna reprezentuje więc odległość między cząstkami (pomiędzy ich powierzchniami) uśrednioną dla wszystkich możliwych par cząstek w rozpatrywanej przestrzeni. Dla cząstek przypadkowo zorientowanych, odległość ta opisuje również przestrzenne (3D) rozproszenie ziaren w analizowanym materiale, ponieważ w takim przypadku, średnia odległość między cząstkami na płaszczyźnie, jest taka sama, jak średnia odległość ziaren w objętości [537].
W przypadku cząstek izometrycznych, średnią odległość swobodną można również łatwo powiązać z rozmiarem ziarna (\(\langle L \rangle\)) zależnością [517, 537]: \[\label{eq:MeanFreeDistanceLavg} \lambda = \langle L \rangle_\alpha \frac{1 - (V_V)_\alpha}{(V_V)_\alpha}.\] Zatem przy określonym udziale objętościowym fazy wtrąconej (\((V_V)_\alpha\)) równanie to stanowi ścisły związek pomiędzy rozmiarem ziaren a średnią odległością swobodną występującą między nimi.
Kolejnym parametrem, który opisuje względne rozmieszczenie cząstek jest odległość między najbliższymi sąsiadami (NND, ang. Nearest-Neighbor Distance). Dla elementów punktowych (albo cząstek o znikomym rozmiarze) średnia odległość między najbliższymi sąsiadami (\(\Delta\)) określona jest równaniami [537]: \[\label{eq:NND3D} \Delta_{\text{3D}} = 0.554/\sqrt[3]{P_V},\] \[\label{eq:NND2D} \Delta_{\text{2D}} = 0.500/\sqrt{P_A},\] w których \(P_V\) i \(P_A\), odpowiadają liczbie punktów przypadających odpowiednio: na jednostkową objętość albo powierzchnię, a wartości współczynników proporcjonalności obliczone są na podstawie prawdopodobieństwa napotkania elementu punktowego wewnątrz sfery (w przypadku 3D) albo koła (2D) [537].
Dla elementów objętościowych (cząstek niebędących elementami punktowymi), NND definiowana jest jako najmniejsza odległość między powierzchniami sąsiadujących cząstek. Parametry \(P_V\) i \(P_A\) w powyższych równaniach zastępowane są wtedy odpowiednimi liczebnościami cząstek \(N_V\) albo \(N_A\).
W przypadku cząstek sferycznych o średnicy \(D\) równania \eqref{eq:NND3D} i \eqref{eq:NND2D} można powiązać z wcześniej określoną średnią odległością swobodną [537]: \[\label{eq:NND3Dlambda} \Delta_{\text{3D}} = 0.554\sqrt[3]{\frac{\pi}{4} D^2 \lambda}\,,\] \[\label{eq:NND2Dlambda} \Delta_{\text{2D}} = 0.500\sqrt{\frac{\pi}{4} D \lambda}\,.\]
Opisane do tej pory wybrane cech mikrostruktury, które można charakteryzować ilościowo przy pomocy szerokiego zestawu parametrów, wykazują wyraźną zmienność w obrębie badanej populacji. Szczególnie istotna jest zmienność rozmiaru i kształtu ziaren. Własność ta jest typowa zarówno dla polikryształów jednofazowych, w których pokrój i rozmiar krystalitów nie jest stały, jak i materiałów wielofazowych, a w szczególności kompozytów ziarnistych. W takich układach zmienność wymienionych cech dotyczy polikrystalicznej osnowy, ale również ziaren fazy wtrąconej.
Parametry mikrostruktury, uzyskane z bezpośrednich pomiarów przeprowadzonych na losowych przekrojach (obrazach mikrostruktury, rys. 2.3a), mogą stanowić podstawę do wstępnej oceny rozmiaru cząstek. W tym celu, najczęściej wykorzystywanym parametrem jest powierzchnia zmierzonych na obrazie cząstek \(S\) albo odpowiadająca im średnica równoważna \(d\). Ponieważ rozmiary cząstek wyznaczane na dwuwymiarowych obrazach nie odpowiadają rzeczywistym rozmiarom (3D) ziaren czy krystalitów, to dane takie (bez dodatkowych korekcji) mogą stanowić materiał jedynie do analiz porównawczych. W praktyce, w takim celu, zebrane dane przedstawiane są w postaci histogramów rozkładu parametrów charakteryzujących rozmiar. Przykładowy histogram rozkładu powierzchni cząstek dla polikrystalicznego tlenku glinu, został przedstawiony na rysunku 2.3b.
W kontekście zmienności przestrzennej można rozpatrywać również orientację cząstek. Aby jednoznacznie określić występowanie uprzywilejowanych kierunków w orientacji osi krystalograficznych krystalitów budujących materiał, niezbędne są pomiary strukturalne (np. EBSD). Jednak, w przypadku mikrostruktury zawierającej cząstki nieizometryczne (szczególnie płytkowe czy w kształcie słupów), analiza przeprowadzona na podstawie dwuwymiarowych przekrojów może dać wstępne wskazówki o możliwości występowania niejednorodności w rozkładzie orientacji krystalitów 47. Prostą metodą, która pozwala na określenie orientacji cząstek, jest porównanie liczby przecięć granic zliczanych na testowych prostych, rzucanych na obraz mikrostruktury pod różnymi kątami \(P_L(\beta)\). Często wykorzystywane są również charakterystyczne kąty \(\theta_\text{max}\) związane z maksymalnymi średnicami Fereta, określającymi wydłużenie cząstek. Badanie rozkładu tych kątów pozwala stwierdzić niejednorodność orientacji. Dane zebrane w takich pomiarach są przedstawiane zwykle w postaci wykresów kołowych (róży kierunków, rys. 2.3c) i mogą być następnie wykorzystywane do ilościowej oceny anizotropii [530, 531, 537].
Jak już wcześniej zaznaczono, rzeczywisty kształt ziaren nie jest możliwy do odtworzenia przy pomocy klasycznych metod opierających się na pojedynczych losowych przekrojach. Obserwowana na przekrojach zmienność kształtów cząstek, wynika bowiem zarówno z właściwych różnic pomiędzy poszczególnymi ziarnami jak i z przypadkowego ich ułożenia – orientacji i wysokości przecięcia przez płaszczyznę obserwacji (zgład). Problem ten został pierwotnie podjęty i teoretycznie opisany przez Wicksella [542, 543]. Zaproponowane przez niego rozwiązanie opiera się na funkcjach rozkładu częstości, które powiązane są uniwersalnym równaniem transformacji [542]: \[\label{eq:Wicksell} f(d) = \frac{d}{\langle D \rangle} \int\limits_{d}^{D_{\text{max}}}\!\!\!\frac{F(D)}{\sqrt{D^2 - d^2}}\mathop{}\!\mathrm{d}D, \quad \text{dla } 0 \leqslant d \leqslant D_{\text{max}},\] przy czym \(f(d)\) jest funkcją rozkładu częstości średnic cząstek \(d\), obserwowanych na losowym przekroju przeprowadzonym przez przestrzenny układ sferoid, których rozkład częstości średnic \(D\) określony jest funkcją \(F(D)\), a \(D_{\text{max}}\) jest maksymalną wartością średnic sferoid \(D\) i tym samym przekrojów \(d\).
Dla z góry przyjętej postaci funkcji \(f(d)\), ustalonej na podstawie pomiarów średnic cząstek na obrazach mikrostruktury albo wyprowadzonej teoretycznie, możliwe jest więc (w oparciu o powyższe równanie) wyznaczenie funkcji opisującej rozkład częstości średnic trójwymiarowych cząstek – sferoid przybliżających rzeczywisty kształt ziaren czy krystalitów. W ujęciu matematycznym jest to zagadnienie odwrotne, opisane równaniem całkowym Volterry pierwszego rodzaju [544, 545], należy więc do równań, które określane są jako zagadnienia źle uwarunkowane. Powoduje to niestabilność rozwiązań numerycznych, co oznacza, że niewielkie błędy w opisie rozkładu częstości średnic przekrojów (w funkcji \(f(d)\)), wywołują duże błędy w estymowanym rozkładzie średnic cząstek \(F(D)\) [544, 546–548].
W praktyce stosowane są więc dwa podejścia pozwalające na uzyskanie, na podstawie dwuwymiarowych losowych przekrojów, rozkładu rozmiaru cząstek (3D). Jeśli znane jest równanie parametryczne opisujące rozkład statystyczny \(F(D)\), to na podstawie równania \eqref{eq:Wicksell}, najczęściej metodami numerycznymi, wyznaczany jest związek pozwalający na transformację \(f(d) \rightarrow F(D)\). Wymaga to jednak przyjęcia a priori określonego rozkładu, który w takim przypadku powinien zostać ustalony wcześniej, na podstawie niezależnych pomiarów przeprowadzonych innymi metodami. Dodatkowo wykorzystywane równanie opisujące rozkład, powinno zawierać niewielką liczbę parametrów, tak aby możliwe było ich numeryczne dopasowanie do danych doświadczalnych w oparciu o ogólne równanie transformacyjne Wicksella. Dlatego w rozwiązaniach tego typu stosowane jest przybliżenie dotyczące jednakowego kształtu cząstek, reprezentowanych przez proste figury przestrzenne (sferoidy czy rzadziej prostopadłościany), a zmienność rozmiaru opisywana jest rozkładem normalnym, logarytmiczno-normalnym, Weibulla, a niekiedy stosowane są złożenia kilku rozkładów tego samego typu [237, 549–551].
Inny, często stosowany typ rozwiązań problemu Wicksella, stanowią metody, które nie wymagają znajomości równania opisującego rozkład rozmiaru cząstek (3D). Opierają się one na parametrach bezpośrednio wyznaczonych z pomiarów przeprowadzonych na obrazach mikrostruktury. Parametry te, opisujące rozmiar cząstek, przedstawiane są w postaci histogramów. W założeniu przyjmuje się, że przedziały klasowe histogramu odpowiadają rozmiarowi największych przekrojów dla kolejnych grup cząstek, a tym samym rzeczywistym rozmiarom cząstek w grupie. Zagadnienie sprowadza się więc do rozłożenia kolejnych przedziałów klasowych, tak aby ustalić faktyczną liczebność cząstek o określonym rozmiarze (3D). Pierwsze rozwiązanie tego problemu dla kulistych cząstek przedstawił Scheil [552], a następnie zostało ono rozwinięte przez Schwartza [553] i Sałtykowa [538]. Metoda Scheila–Schwartza–Sałtykowa (SSS) opiera się na prawdopodobieństwie przecięcia sferycznej cząstki o promieniu \(R\) przez płaszczyznę usytuowaną na wysokości pomiędzy \(h_i\) a \(h_{i+1}\) (\(h \leqslant 2R\)). Prawdopodobieństwo to można ustalić na podstawie prostych związków geometrycznych i dodatkowo powiązać z promieniem kolistego przekroju \(r\), który powstanie na skutek takiego przecięcia [517, 537]: \[\label{eq:prob_slice} p_{i,j} = \frac{h_{i-1}-h_i}{R_j} = \frac{1}{R_j} \left(\sqrt{R_j^2 - r_{i-1}^2} - \sqrt{R_j^2 - r_{i}^2}\, \right)\!,\] przy czym indeks \(i\) odpowiada kolejnym przekrojom, a indeks \(j\) odnosi się do sferycznych cząstek o różnych promieniach (w układzie monodyspersyjnym \(j = 1\)).
Wykorzystując prawdopodobieństwo przecięcia cząstki, liczbę cząstek obserwowanych na przekrojach można wyrazić sumą: \[\label{eq:SaltykovNaP} (N_A)_i = \Delta \sum\limits_{j=1}^{k} p_{i,j} (N_V)_j,\] w której \(\Delta = D_{\text{max}}/k\), gdzie \(D_{\text{max}}\) jest średnicą największej cząstki (w praktyce maksymalną średnicą równoważną wyznaczoną na obrazie mikrostruktury), a \(k\) liczbą klas histogramu. Na całkowitą liczbę cząstek \((N_A)_i\) zawartą w danej klasie histogramu, składają się więc cząstki o różnych promieniach \(R\), których przekroje posiadają średnice w zakresie między \(r_i\) a \(r_{i-1}\). Wyrażenie powyższe \eqref{eq:SaltykovNaP}, reprezentuje więc zespół równań liniowych, z których można wyznaczyć nieznaną liczbę cząstek przypadającą na jednostkową objętość \((N_V)_j\) dla kolejnych klas histogramu.
Oryginalna procedura przedstawiona w metodzie SSS, pozwalająca na obliczenie wartości \((N_V)_j\), opiera się sukcesywnym odejmowaniu liczebności w kolejnych klasach, co można zapisać w postaci równania [554, 555]: \[\label{eq:SaltykovNv} (N_V)_j = \frac{1}{\Delta} \sum\limits_{i=j}^{k} \alpha_{j,i} (N_A)_i,\] w którym współczynniki \(\alpha_{j,i}\), nazywane macierzą transformacyjną, mają ujemną wartość dla \(i > j\), a dodatnią jedynie dla \(i = j\) (dla \(i < j\) nie są określone). Zatem, za wyjątkiem największych cząstek w klasie (\(i = j\)), pozostałe iloczyny \(\alpha_{j,i} (N_A)_i\) są ujemne. Procedurę tę przeprowadza się kolejno dla wszystkich klas, począwszy od największego rozmiaru cząstek, aż do wyczerpania wszystkich przedziałów i odtworzenia rozkładu \(N_V\).
Wartości współczynników \(\alpha_{j,i}\) zależą od przyjętego kształtu cząstek. W klasycznej metodzie SSS, wartości te zostały wyznaczone dla cząstek kulistych [537, 538, 554], ale odpowiednie macierze transformacyjne zostały również wyliczone dla cząstek niekulistych – sferiodalnych i prostopadłościennych [556]. Podobne w założeniach są też rozwiązania zaproponowane przez Cruz-Orive [557, 558] i Woodheada [559], a różnice polegają na doborze punktów centralnych i przedziałów klasowych w histogramach [560].
Metoda SSS i metody pokrewne, opierające się na histogramach, są nadal przedmiotem wielu prac. Przyjęcie nieodpowiedniego podziału klasowego, przy określonej liczebności próby i rozdzielczości obrazu mikrostruktury, może powodować błędy numeryczne. Szerokie przedziały, zawierające dużą liczbę cząstek, pozwalają uzyskać dużą stabilność rozwiązań, jednak zmniejszają dokładność odwzorowania zmienności. Z kolei duża liczba przedziałów, wiernie oddająca rozkład badanej cechy, może powodować pojawienie się ujemnych wartości liczebności. Wynikają one z niedostatecznej ilości cząstek, zaobserwowanych i zmierzonych na analizowanych obrazach, w określonym przedziale klasowym [554, 556, 561–567]. Pojawienie się takich niefizycznych wartości liczebności, wymaga dodatkowej renormalizacji histogramu, co niekorzystnie wpływa na ostateczną dokładność transformacji [563, 565, 566].
Założenia dotyczące kształtu, a w szczególności wypukłości cząstek, są niezbędne do określenia rozkładu ich rozmiaru (3D). Dla dowolnych kształtów nie istnieje rozwiązanie analityczne, tego istotnego zagadnienia stereologicznego [549, 563]. Jednak dla wielu polikryształów ceramicznych jak również kompozytów ziarnistych, takie przybliżenia są akceptowalne – kształt, przyjmowanych w rozwiązaniach, modelowych figur nie odbiegają znacząco od rzeczywistego kształtu krystalitów czy cząstek fazy wtrąconej (por. rys. 1.1 a i b). Jeśli więc pokrój ziaren zbliżony jest do izometrycznego, to zastosowanie modelu opartego na kulistych cząstkach, pozwala estymować rozkład rozmiaru ziaren w 3D z niewielkim błędem wynikającym z przyjętych założeń [517], jedynie na podstawie obserwacji i pomiarów wykonanych na dwuwymiarowych, losowych obrazach mikrostruktury.
Metody oparte na transformacji histogramu pozwalają zatem na jakościową ocenę rozkładu rozmiaru cząstek. Uzyskane w ten sposób wyniki, mogą stanowić ważny element w opisie mikrostruktury. Aby jednak w pełni, ilościowo scharakteryzować zróżnicowanie rozmiaru cząstek w analizowanym materiale, a w szczególności wykorzystać uzyskane dane do trójwymiarowej rekonstrukcji mikrostruktury, niezbędny jest opis ilościowy. Można w tym celu zastosować metodę dwuetapową [567]. W etapie pierwszym, histogram rozkładu średnic równoważnych cząstek \(d\), uzyskany z analizy obrazów mikrostruktury, transformuje się do histogramu rozkładu średnic trójwymiarowych cząstek \(D\). Dla materiałów ceramicznych, wykorzystuje się w tym kroku najczęściej metodę SSS. Następnie uzyskany w ten sposób histogram, reprezentujący empiryczny (dyskretny) rozkład rozmiaru cząstek (3D), poddawany jest dopasowaniu rozkładem teoretycznym (zwykle normalnym, logarytmiczno-normalnym albo Weibulla). Takie postępowanie pozwala na uzyskanie w pełni ilościowego opisu analizowanego rozkładu, poprzez podanie kilku parametrów charakterystycznych dla dopasowanego rozkładu teoretycznego [540, 541, 567, 568]. Wyniki przykładowej transformacji, wykonanej metodą dwuetapową, przedstawia rys. 2.4.
Oprócz rozkładów analizowanych parametrów, wyrażonych graficznie w formie histogramów, czy też poprzez równania odpowiadające rozkładom teoretycznym, zmienność cech mikrostruktury, opisywana jest również momentami statystycznymi wyższych rzędów: wariancją, odchyleniem standardowym, współczynnikiem wariancji (zmienności), współczynnikiem skośności i in. [237, 517, 519, 530, 537]. Jednak znaczący postęp w ilościowym opisie, dokonał się dzięki zastosowaniu statystycznych deskryptorów rozkładu przestrzennego [218, 555, 569, 570]. Najczęściej stosowanymi deskryptorami są funkcje korelacji \(n\)-punktowej (autokorelacji) [523, 555, 571–574], funkcje rozkładu długości cięciw czy odległości swobodnej (korelacji liniowej) [575–577], funkcje rozkładu odległości między najbliższymi sąsiadami [578–582] oraz deskryptory entropowe [583, 584].
Dla zilustrowania koncepcji opartych na statystycznych deskryptorach rozkładu przestrzennego, można przedstawić nieco szerzej funkcję korelacji \(n\)-punktowej. W materiale dwufazowym (np. kompozycie ziarnistym), funkcja korelacji dwupunktowej \(S_2\) (\(n = 2\)) jest miarą prawdopodobieństwa, odpowiadającego zdarzeniu, że dwa punkty \(x_1\) i \(x_2\), losowo rozmieszczone wewnątrz materiału, jednocześnie znajdą się w obszarze \(\Omega^i\) zajmowanym przez wybraną fazę \(i\). Można to zapisać w postaci równania [218, 571]: \[\label{eq:2pointCorTorquato} S_2^i = \langle I^i(x_1) I^i(x_2) \rangle,\] przy czym \(\langle\, \rangle\) oznacza uśrednianie dla całej próby, a \(I^i(x)\) jest funkcją zdefiniowaną równaniem [218, 571]: \[\label{eq:2pointCorTorquatoIf} I^i(x) = \begin{cases} 1 & \quad \text{jeśli } x \in \Omega^i, \\ 0 & \quad \text{w pozostałych przypadkach}. \end{cases}\] Podczas analizy prowadzonej na dwuwymiarowych obrazach mikrostruktury, funkcję korelacji dwupunktowej wygodnie jest przedstawiać w układzie współrzędnych biegunowych jako \(S_2^i(r,\phi)\), w którym \(r\) jest odległością między punktami \(x_1\) i \(x_2\) (na płaszczyźnie obrazu) oraz \(\phi\) kątem pomiędzy prostą łączącą punkty a wybranym kierunkiem głównym na obrazie. W ogólnym przypadku, kąt \(\phi\) w kolejnych powtórzeniach przyjmuje dowolne (losowe) wartości. Można jednak przyjąć również stałe wartość kąta (np. \(\phi =\)0 °, albo \(\phi =\)90 °) i uzyskać tym samym kierunkowe funkcje korelacji dwupunktowej [572]. Dodatkowo, funkcja \(S_2^i\) przyjmuje maksymalną wartość dla \(r = 0\), równą udziałowi objętościowemu \(i\)-tej fazy \(V_i\), a wraz ze wzrostem długości promienia \(r\) (odległości między losowymi punktami) zdąża do \(V_i^2\) [571, 585, 586].
Wyniki przykładowej analizy rozkładu przestrzennego, w postaci funkcji korelacji dwupunktowej, przedstawione zostały na rysunku 2.5. Szybkość zaniku korelacji (obniżania wartości \(S_2\) wraz ze wzrostem odległości \(r\)) jest największa w zakresie niewielkich wartości \(r\). Zanika wtedy korelacja krótkiego zasięgu. Dla struktur jednorodnych, które nie wykazują uporządkowania dalekiego zasięgu, po przekroczeniu pewnej odległości, wartość \(S_2\) stabilizuje się. Zmiany te można przedstawić eksponencjalną zależnością wprowadzoną przez Debye’a [587, 588]: \[\label{eq:Debye} f_{\text{D}}(r) = \exp (-\frac{r}{a_{\text{cl}}}),\] w której \(a_{\text{cl}}\) jest parametrem nazywanym odległością korelacji. W przypadku rzeczywistych struktur, dla większych wartości \(r\), na krzywej \(S_2(r)\) mogą pojawić się fluktuacje, wskazujące na występowanie korelacji dalekiego zasięgu. Korelacje takie mogą wynikać z grupowania przestrzennego – aglomeracji (klasteryzacji struktury) albo periodyczności w rozmieszczeniu cząstek (zob. rys. 2.5b).
Do opisu takich fluktuacji można zastosować równanie zaproponowane przez Cule i Torquato [571, 589]: \[\label{eq:Cule-TorquatoS2} S_2(r) = V_i(1-V_i) f_{\text{D}}(r) \frac{\sin(2\pi r/b)}{2\pi r/b} + V_i^2,\] w którym parametr \(b\) wyraża charakterystyczną długość kontrolującą fluktuacje opisywane przez \(\sin(2\pi r/b)/(2\pi r/b)\).
W analizie zmienności przestrzennej mikrostruktury, pomocne są również kierunkowe funkcje korelacji. Różnice w funkcjach \(S_2^i(r,\phi)\), wyznaczonych przy ustalonych wartościach kątów \(\psi\) w porównaniu do \(S_2^i(r)\), a w szczególności obecne dla nich fluktuacje korelacji dalekiego zasięgu, które można zaobserwować również na wykresach przedstawionych na rys. 2.5c, wskazują na kierunkową niejednorodność rozmieszczenia cząstek (kierunkową aglomerację), a tym samym możliwość występowania tekstury i anizotropii badanego tworzywa.
Funkcje korelacji \(n\)-punktowej – a także pozostałe, wymienione wcześniej, statystyczne deskryptory rozkładu przestrzennego – oprócz analizy porównawczej i ilościowej, przeprowadzanej dla rzeczywistych mikrostruktur, wykorzystuje się również do generowania struktur stochastycznych. W tym zakresie, statystyczne deskryptory rozkładu przestrzennego pełnią rolę funkcji, na podstawie których przeprowadzana jest optymalizacja struktury stochastycznej. W efekcie, uzyskiwana jest struktura statystycznie równoważna rzeczywistej – opisywanej wybranym deskryptorem, albo całkowicie syntetyczna – stanowiąca modelowe (geometryczne) odwzorowanie struktury rozważanej teoretycznie [590–601].
W polikrystalicznych tworzywach ceramicznych (polikryształach kowalencyjno-jonowych), kształt krystalitów jest uwarunkowany symetrią sieci krystalicznej znacznie silniej, niż ma to miejsce w materiałach metalicznych, w których z uwagi na możliwość wystąpienia odkształceń plastycznych, kierunkowa deformacja ziaren może wynikać również z procesu obróbki plastycznej (walcowania, kucia itp.).↩︎
W tym podrozdziale zostaną omówione wybrane elementy przetwarzania i analizy obrazu w zakresie wykorzystywanym do pozyskania informacji o mikrostrukturze materiałów. Choć ogólny schemat postępowania w wielu dziedzinach jest podobny, to jednak specyfika, złożoność zagadnień i różne cele, dla których przetwarzane i analizowane są cyfrowe obrazy, powodują, że ścieżki postępowania oraz wykorzystywane techniki mogą się od siebie znacząco różnić [532]. Na wstępie należy również zaznaczyć, że sam podział na przetwarzanie i analizę obrazu nie ma wyraźnie określonych ram [602], a elementy te stanowią kolejne kroki w całym łańcuchu czynności niezbędnych do pozyskania jakościowej i ilościowej informacji o budowie materiału.
W inżynierii materiałowej, typowy tok postępowania, mający na celu opisanie mikrostruktury na podstawie cyfrowych obrazów, rozpoczyna się od przygotowania powierzchni materiału (cięcie, szlifowanie, polerowanie, trawienie). Następnie próbki obserwowane są przy pomocy technik mikroskopowych (SEM, TEM, optyczne), a wyniki obserwacji, zbierane i zapisywane w postaci cyfrowej (plików graficznych). Tak zgromadzone informacje stanowią dane wejściowe do wstępnego przetwarzania obrazu (IP, ang. image processing), po którym, w kolejnym kroku, wykorzystywane są do analizy obrazu (IA, ang. image analysis). Cała procedura badawcza kończy się zazwyczaj na analizie jakościowej, ilościowej i interpretacji uzyskanych wyników [530, 535, 603]. Wszystkie wymienione etapy są więc równie istotne i na każdym z nich niezbędna jest weryfikacja uzyskanych efektów. Wszelkie niedoskonałości podczas przygotowania powierzchni do obserwacji mikrostruktury (np. rysy, zabrudzenia, niedostateczne albo nadmierne wytrawienie powierzchni) [390, 604], błędy podczas zbierania cyfrowych obrazów (np. zbyt mała rozdzielczość, nierównomierność oświetlenia tła, stratny format plików cyfrowych), wprowadzają do obrazu mikrostruktury artefakty, które mogą być trudne lub wręcz niemożliwe do usunięcia na etapie przetwarzania obrazu i następnie powodować błędy w analizie obrazu [518, 532].

W przedstawionym toku postępowania, etapy przetwarzania i analizy obrazu, stanowią więc elementy łączące bezpośredni pomiar (obserwację) z analizą i interpretacją danych, prowadzoną opisanymi w poprzednim podrozdziale metodami stereologicznymi, które następnie mogą zostać wykorzystane także do rekonstrukcji mikrostruktury (przykładowe kroki IP oraz IA zawiera rys. 2.6).
Wszelkie operacje związane z przetwarzaniem i analizą obrazu, dotyczą więc cyfrowych danych reprezentujących obserwowany obiekt (powierzchnię próbki). Dane takie uzyskiwane są w trakcie akwizycji obrazu, podczas której dochodzi do próbkowania przestrzennego oraz dyskretyzacji sygnału [602, 605]. W efekcie cyfrowy obraz charakteryzuje się określoną rozdzielczością przestrzenną, zależną od liczby punktów próbkowania i rozdzielczością poziomów jasności (intensywności), związaną z maksymalną liczbą wartości luminancji, która może zostać zarejestrowana i zapisana. Wszystkie te informacje są zwykle przedstawiane w postaci macierzy \(L(m,n)\), w której indeksy \(m\) i \(n\) określają pozycję punktu próbkowania w płaszczyźnie obrazu. Pojedynczy element macierzy nazywany jest pikselem i zawiera informacje o poziomie jasności. W obrazie binarnym, do zapisu jasności wykorzystywany jest jeden bit na każdy piksel, czyli jasność może przyjąć dwie wartości (\(2^1\)). Jest to najbardziej zredukowany sposób zapisu informacji, ale jest najczęściej wykorzystywany w analizie obrazu. Obrazy zapisywane w skali szarości zwykle posiadają 256 poziomów jasności (poziomów szarości), co wymaga zapisu 8 bitów na piksel. Dla obrazów kolorowych, niezależnie zapisywane są informacje o trzech jego składowych: czerwonej, zielonej i niebieskiej (\(3\cdot\)8 bit/piksel). Niektóre mikroskopy, pozwalają również przechwytywać i zapisywać obrazy z większą głębią bitową (ponad 8 bit/piksel), co istotnie poprawia odwzorowanie przejść tonalnych i w niektórych zastosowaniach może zapewnić dokładniejszą analizę [602]. Przekształcenia cyfrowego obrazu na etapie jego przetwarzania oraz wiele operacji składających się na analizę obrazu, polega zatem na zmianie pozycji lub wartości poszczególnych elementów (pikseli) w macierzy \(\mathbf{L}\), albo na wyodrębnianiu z niej informacji poprzez narzucone warunki wyboru.
Przetwarzanie obrazu jest pierwszym etapem, w którym dochodzi do przekształcenia cyfrowych danych. Niskopoziomowe operacje przetwarzania obrazu, takie jak korekcja geometrii układu optycznego, czy wstępne usuwanie cyfrowego szumu, mogą być realizowane automatycznie (programowo) w układzie procesora obrazu na podstawie tablic korekcyjnych (LUT, ang. Look-Up Table). Wstępnie skorygowane obrazy, zapisane w postaci plików graficznych, są następnie poddawane dalszemu przetwarzaniu, mającemu na celu uwypuklenie istotnych cech, a usunięcie artefaktów, zniekształceń, nierównomierności oświetlenia oraz pozostałego cyfrowego szumu. Wykorzystywane są w tym celu: przekształcenia punktowe (bezkontekstowe), filtry (przekształcenia kontekstowe), przekształcenia widmowe, morfologiczne i rzadziej przekształcenia geometryczne [605]. Te ostatnie, polegające na przesunięciu, rotacji, odbiciu i innych transformacjach geometrycznych obrazu (reprezentowanego przez macierz \(L(m,n)\)), stosowane są w układach korekcyjnych i zwykle nie są wykorzystywane w dalszych etapach przetwarzania obrazu.
Uniwersalnymi przekształceniami poprawiającymi czytelność obrazu, które zwykle stosuje się na wstępnym etapie prac, są: normalizacja i wyrównanie histogramu [518, 603]. Należą one do przekształceń punktowych, czyli takich, które polegają na modyfikacji poziomu jasności poszczególnych pikseli, bez względu na stan pikseli z nimi sąsiadujących. W przypadku normalizacji i wyrównywania histogramu, przekształcenia te dotyczą jednocześnie całych grup pikseli, należących do określonej klasy w histogramie 48. Normalizacja polega na zmianie zakresu wartości jasności pikseli dla każdego przedziału, tak aby histogram obrazu wynikowego pokrywał cały zakres rozpiętości tonalnej (np. od 0 do 255) [518, 532]. W przypadku zastosowania normalizacji przy pomocy funkcji liniowej, przekształcenie to można zapisać w postaci równania: \[\label{eq:hist_norm} L'(m,n) = \left[L(m,n) - L_{\text{min}}\right]\frac{L'_{\text{max}} - L'_{\text{min}}}{L_{\text{max}} - L_{\text{min}}} + L'_{\text{min}},\] w którym \(L'(m,n)\) jest macierzą reprezentującą obraz wynikowy, \(L_{\text{max}}\) i \(L_{\text{min}}\) odpowiadają maksymalnej i minimalnej wartości jasności pikseli na przekształcanym obrazie \(L(m,n)\), a \(L'_{\text{max}}\) i \(L'_{\text{min}}\) założonym wartościom jasności po normalizacji. Przekształcenie to może być również stosowane, aby sprowadzić zbyt szeroki zakres tonalny, będący wynikiem przeprowadzonych na obrazie operacji, do zakresu węższego, odpowiadającego przyjętej głębi bitowej.
W przypadku przekształcenia prowadzącego do wyrównania histogramu, wartość jasności dla kolejnych klas jest modyfikowana tak, aby uzyskać równomierny rozkład częstości w całym zakresie jasności. Uzyskuje się to poprzez przypisanie kolejnym poziomom jasności \(j\) oryginalnego obrazu, nowej wartości \(k\), którą można wyznaczyć z równania [532, 602]: \[\label{eq:hist_equalize} k = n_L \sum\limits_{i=0}^{j} \frac{n_i}{MN},\] w którym \(n_L\) jest liczbą poziomów jasności (np. dla obrazu o głębi 8 bit/piksel, \(n_L = 256\)), \(n_i\) liczebnością pikseli w \(i\)-tej klasie jasności, a iloczyn \(MN\) określa całkowitą liczbę pikseli w obrazie o wymiarach \(M \times N\) pikseli (powierzchnię pod histogramem).
Efekty działania przedstawionych operacji są szczególnie widoczne dla detali, których kontrast jest niewielki i są usytuowane w obszarach o małej albo dużej jasności. Przekształcenia te nie wprowadzają, ani nie redukują, informacji obecnych w obrazie, ale przeprowadzone na wstępie, pozwalają lepiej ocenić zakres wymaganych prac i zaplanować dalszy ich przebieg [518, 532].
Pozostałe przekształcenia punktowe, które są często stosowane podczas przetwarzania cyfrowych obrazów, takie jak: rozjaśnianie, przyciemnianie oraz gamma modulacja, polegają na modyfikacji wartości jasności poprzez operacje arytmetyczne: dodawanie, mnożenie wartości \(L(m,n)\) przez ustaloną stałą lub potęgowanie (\(L(m,n)^\gamma\), w przypadku gamma modulacji) [605].
Do drugiej grupy operacji, wykorzystywanych podczas przetwarzania obrazów, zaliczane są przekształcenia kontekstowe. Filtracja danych zawartych w obrazie, polegająca na zmianie wartości jasności kolejnych pikseli, przebiega tutaj zależnie od wartości jasności innych pikseli. Stosowane w tym celu filtry liniowe opierają się na mnożeniu splotowym (konwolucji) funkcji opisującej obraz \(L(m,n)\) z funkcją filtrującą \(w(i,j)\), które dla dyskretnych, dwuwymiarowych obrazów cyfrowych, można zapisać w postaci równania [605]: \[\label{eq:konwolucja} L'(m,n) = [w * L](m,n) = \sum\limits_{i}\sum\limits_{j} w(i,j) L(m-i,n-j).\] Macierz \(w(i,j)\), reprezentująca funkcję filtrującą, jest nazywana maską, a jej współczynniki stanowią wagi do obliczenia średniej wartości jasności. Rozmiar maski zależy od liczby pikseli, których jasność jest brana pod uwagę, przy filtrowaniu. Zwykle są to macierze \(3 \times 3\), \(5 \times 5\) i \(7 \times 7\), w których centralny element reprezentuje piksel dla którego wykonywane jest filtrowanie. Średnia wartość jasności, obliczona wewnątrz maski, jest następnie wykorzystywana do wyznaczenia nowych wartości jasności dla pikseli wewnątrz maski z uwzględnieniem ich wag.
Filtry liniowe są zwykle wykorzystywane do usuwania niepożądanego szumu na obrazie. Stosuje się w tym celu filtry dolnoprzepustowe (uśredniające), które tłumią elementy o wysokiej zmienności (np. drobne szczegóły o rozmiarze jednego albo dwóch pikseli) i w efekcie, uzyskany po filtracji obraz, jest pozbawiony dużych gradientów jasności (jest wygładzony). Odwrotne działanie mają filtry górnoprzepustowe, które z kolei stosowane są do wzmacniania szczegółów obecnych na obrazie. Wzmacniają one elementy o wysokiej zmienności i dzięki temu powodują wyostrzenie obrazu, ale również zwiększenie szumu.
Działanie filtrów nieliniowych opiera się również na maskach, jednak do filtracji nie jest wykorzystywana konwolucja, tylko wybierana jest jedna z wartości jasności, wśród pikseli leżących w obszarze maski. Przykładem jest filtr medianowy, który wybiera wartość środkową jasności dla pikseli wewnątrz maski i przypisuje ją do filtrowanego piksela. Filtr medianowy, podobnie jak filtry dolnoprzepustowe, usuwa drobne szczegóły, jednak nie powoduje tak znacznego wygładzania i przez to znacznie lepiej zachowuje krawędzie obecne w przetwarzanym obrazie [518, 603].
Często występującym problemem, utrudniającym późniejszą analizę ilościową obrazu, jest nierównomierne oświetlenie powierzchni próbki. Zjawisko to ujawnia się szczególnie w przypadku obserwacji prowadzonych przy pomocy mikroskopów optycznych. Pomijając wady układu optycznego i kamery rejestrującej obraz, które powinny zostać skorygowane na etapie akwizycji i wstępnego niskopoziomowego przetwarzania, nierównomierne oświetlenie powierzchni może być również spowodowane kształtem próbki (odstępstwem od płasko-równoległości) oraz nieodpowiednim jej zamocowaniem w mikroskopie [519]. Niewielkie nierównomierności oświetlenia są zwykle trudne do ustalenia na podstawie obserwacji nieprzetworzonych (,,surowych”) obrazów. Dlatego wady te zazwyczaj nie przeszkadzają w analizie jakościowej mikrostruktury. Stają się one jednak wyraźnie po wstępnych etapach przetwarzania obrazu (normalizacji albo wyrównaniu histogramu) i, szczególnie gdy kontrast pomiędzy istotnymi elementami mikrostruktury jest niewielki, mogą utrudniać późniejszą, poprawną segmentację.
Jeśli więc nie jest możliwe ponowne przeprowadzenie obserwacji i wyeliminowanie nierównomierności oświetlenia podczas pozyskiwania obrazu, to na etapie przetwarzania stosowane są techniki korekcji oświetlenia (wyrównywania tła). Opierają się one na założeniu, że zarejestrowany obraz jest złożeniem informacji o właściwej mikrostrukturze próbki i nierównomiernie oświetlonym tle (cieniu) [606]. Wyodrębnienie z obrazu cienia, pozwala więc na skuteczną jego korekcję.
Lokalne zmiany jasności wywołane cieniem są stosunkowo niewielkie. Dlatego przydatne na tym etapie są przekształcenia wykorzystujące globalną zmienność jasności. Pomijając możliwość dodatkowych pomiarów nierównomierności oświetlenia (zapis obrazu jednorodnej powierzchni, przeprowadzony w tych samych warunkach pomiarowych), informacje takie można uzyskać na podstawie przyjętego modelu oświetlenia, albo bezpośrednio z zarejestrowanego obrazu powierzchni próbki [532, 607]. W pierwszym przypadku generowany jest obraz zawierający jedynie gradient jasności (cień), który następnie odejmowany jest od korygowanego obrazu. Gradient taki może zostać utworzony na podstawie jasności pikseli leżących na obrzeżu przetwarzanego obrazu, a wartości jasności pozostałych (wewnętrznych) pikseli są uzyskiwane na podstawie interpolacji wielomianowej. Niekiedy do utworzenia gradientu wykorzystywane są również zmierzone jasności pikseli wewnątrz obrazu, co pozwala odwzorować bardziej złożony rozkład cienia. Metoda ta daje dobre efekty w przypadku obrazów zawierających niewielkie elementy wyraźnie oddzielone od tła (np. wtrącenia od osnowy).
Druga grupa metod wyrównywania niejednorodności oświetlenia opiera się bezpośrednio na zarejestrowanym obrazie. Na jego podstawie uzyskiwane są niezbędne informacje o globalnym, uśrednionym rozkładzie oświetlenia, co umożliwia korekcję [532, 607]. Do wydzielenia tła z obrazu może zostać wykorzystywany filtr medianowy o dużym rozmiarze maski. Stosowane są również operacje morfologiczne, pozwalające usunąć niewielkie elementy obrazu [518] oraz szereg złożonych algorytmów wykorzystujących filtrowanie częstotliwości w oparciu o transformację Fouriera, skanowanie liniowe czy model toczącej się kuli [518, 532, 607–609].
W przypadku tworzyw polikrystalicznych, zarówno jedno- jak i wielofazowych, istotną cechą mikrostruktury są granice międzyziarnowe. Na etapie przetwarzania obrazu należy więc doprowadzić do uwypuklenia tego elementu, przy jednoczesnym stłumieniu niejednorodności występujących w obrębie ziaren, wynikających z niedoskonałości podczas przygotowania powierzchni. Jedną z możliwości jest zastosowanie klasycznych filtrów wykrywających krawędzie np. filtrów Sobela [610], Robertsa [611] i Prewitt [612].
Przebieg etapu przetwarzania obrazu, a w szczególności dobór stosowanych w nim przekształceń, jest uzależniony od mikrostruktury analizowanego tworzywa oraz od specyfiki zarejestrowanego obrazu. Dlatego w wybranej ścieżce przetwarzania, niektóre z wymienionych operacji mogą być powtarzane kilkukrotnie, a inne, nie będą w niej wykorzystywane. Etap ten należy rozpatrywać, jako przygotowanie danych do dalszej analizy. Dlatego istotne jest, aby w toku przeprowadzanych czynności dokonywać selekcji: usuwać informacje nieistotne – szczególnie szum, artefakty i elementy, które nie będą podlegać dalszej analizie, a pozostawiać i wzmacniać te, które są interesujące w kontekście ilościowej analizy obrazu.
W kontekście przekształceń wykonywanych na cyfrowych obrazach, histogram reprezentuje rozkład jasności dla wszystkich elementów macierzy \(L(m,n)\) (pikseli) i jest narzędziem szeroko stosowanym na wielu etapach przetwarzania obrazu. Liczba klas histogramu jest równa liczbie poziomów jasności w przyjętym formacie cyfrowego obrazu.↩︎
Charakterystyczną cechą tego etapu pracy z cyfrowym obrazem jest radykalna redukcja informacji, która dokonywana jest w jego trakcie. Można zatem powiedzieć, że ,,jest to proces polegający na wyodrębnieniu z całkowitej informacji docierającej do obserwatora bądź detektora tej części, która jest istotna z punktu widzenia użytkownika lub procesu” [605]. Oznacza to, że obraz, który jest wstępnie przetworzony, zostaje zamieniony na niewielki zestaw parametrów (liczb), które opisują wybrane elementy obrazu. Stosowane w tym etapie techniki są zatem silnie uzależnione od celu analizy – znacznie bardziej niż ma to miejsce w przypadku przetwarzania obrazu. Ten sam obraz można więc przekształcać wielowątkowo i uzyskiwać w ten sposób dane opisujące różne elementy budowy materiału.
Kluczowym etapem analizy obrazu jest segmentacja. Polega ona na podziale cyfrowego obrazu na szereg mniejszych elementów spełniających założone kryterium jednorodności. Dokonanie takiego podziału, pozwala następnie na indeksację wydzielonych elementów, przeprowadzenie na nich pomiarów oraz na ich opis, przy pomocy zestawu deskryptorów (parametrów ilościowych). Wymienione kroki są zatem typowe dla analizy obrazów mikrostruktury.
Kryteria podziału obrazu opierają się na jednorodności poziomu jasności, koloru, albo faktury, a stosowane do segmentacji techniki, zależą od typu mikrostruktury jak również od jakości obrazu. W przypadku materiałów inżynierskich, a w szczególności tworzyw ceramicznych, obraz mikrostruktury może być zwykle zaklasyfikowany do jednego z trzech modelowych układów [518, 607]. Pierwszy, składa się z jednorodnej, ciągłej osnowy, w której rozmieszczone są izolowane wtrącenia, istotnie różniące się od niej poziomem jasności. Drugi, reprezentuje materiały jedno- albo wielofazowe, w których wyraźnie widoczna jest ich polikrystaliczna budowa. Trzeci układ odpowiada mikrostrukturze materiałów wielofazowych, w których poszczególne fazy wzajemnie przenikają się tworząc przypadkowe wzory. Przyjęcie takiego rozróżnienia jest przydatne nie tylko w kontekście doboru technik segmentacji, ale przede wszystkim pozwala na ustalenie, jakie elementy mikrostruktury mogą zostać opisane na podstawie analizy obrazu.
Pierwszy typ mikrostruktury pozwala zatem na wyznaczenie wielu parametrów opisujących budowę wtrąceń, a analiza obrazu nie wymaga zazwyczaj stosowania skomplikowanych technik. Duży kontrast między fazami ułatwia segmentację poprzez progowanie (ang. thresholding). Technika ta polega na dobraniu wartości poziomu jasności (progu), tak aby znalazł się on pomiędzy wartościami jasności charakterystycznymi dla faz składowych. Następnie, poprzez porównanie wartości poziomu jasności dla kolejnych pikseli obrazu z progiem, można zaklasyfikować je do jednej z dwóch grup (np. osnowy albo wtrąceń). W efekcie progowania uzyskiwany jest obraz binarny, zawierający jedynie dwie wartości poziomu jasności dla wszystkich pikseli. Wartość progowa może zostać przyjęta w oparciu o analizę histogramu jasności obrazu albo zostać wyznaczona przy pomocy automatycznych algorytmów progowania, które uniezależniają wynik progowania od subiektywnej oceny operatora [518, 603, 613].
Przejście od obrazu w skali szarości (8 bit/piksel) do obrazu binarnego (1 bit/piksel), nazywane binaryzacją, jest przekształceniem powodującym znaczną redukcję informacji. Obraz binarny jest jednak podstawową reprezentacją mikrostruktury wykorzystywaną podczas analizy obrazu. Na podstawie obrazu binarnego można bezpośrednio wyznaczyć główne parametry opisujące cząstki takie jak powierzchnia, obwód oraz współrzędne opisujące wymiary. Dlatego nawet niewielki błąd popełniony na etapie binaryzacji pociąga za sobą poważne rozbieżności w uzyskiwanych wartościach parametrów mikrostruktury.
W przypadku mikrostruktury polikrystalicznej (drugi z wymienionych, typowych układów modelowych) zastosowanie progowania jest często niewystarczające do poprawnej segmentacji. Różnice w poziomie jasności kolejnych ziaren widocznych na obrazie (należących do tej samej fazy), są zbyt duże i mogą pokrywać się z poziomami jasności granic oddzielających poszczególne cząstki. Wykorzystanie zatem jedynie progowania, powoduje znaczące błędy w segmentacji. W takim przypadku, przed binaryzacją, stosowane są filtry wykrywające krawędzie albo, do rozdzielenia poszczególnych elementów widocznych na obrazie, wykorzystywane są bardziej zaawansowane metody opierające się na segmentacji wododziałowej (ang. watershed segmentation), wykorzystujące metody rozrostu obszarów (ang. region growing), grupowania pikseli (ang. clustering methods) oraz wiele innych [602, 607, 614].
Trzeci z wymienionych typów obrazów mikrostruktury jest najtrudniejszy w analizie. Zmiany poziomów jasności cząstek widocznych na obrazie są niejednoznaczne i segmentacja może być obarczona znacznymi błędami. Niekiedy, w tego typu układach, do segmentacji może zostać wykorzystywana faktura obiektów [605, 607]. Informacje ilościowe, które można uzyskać na podstawie analizy obrazu w tego typu układach, często ograniczają się jedynie do ustalenia przybliżonego udziału objętościowego faz składowych.
Niezależnie od typu mikrostruktury, uzyskane w trakcie binaryzacji obrazy wymagają zazwyczaj dodatkowych korekt. Niezbędne jest więc usunięcie artefaktów powstałych w wyniku niedostatecznego usunięcia szumu albo rozdzielanie stykających się obiektów. W tym celu wykorzystywane są przekształcenia morfologiczne. Opierają się one na selektywnej filtracji, która przeprowadzana jest wyłącznie dla pikseli spełniających założone warunki sąsiedztwa. Warunki takie sprawdzane są przy pomocy elementu strukturalnego (podobnego do maski wykorzystywanej podczas filtracji), który przykładany jest kolejno do wszystkich pikseli obrazu. Jeśli lokalna konfiguracja spełnia założony warunek, to na rozpatrywanym pikselu dokonywana jest określona operacja. Wiele operacji morfologicznych może być przeprowadzanych zarówno dla obrazów binarnych jak i dla obrazów w skali szarości.
Najczęściej wykorzystywane przekształcenia morfologiczne to erozja i dylatacja, które powodują zmianę poziomu jasności pikseli leżących na krawędziach jednorodnych obszarów. W przypadku obrazów binarnych, erozja prowadzi do zmniejszania rozmiaru elementów obrazu, których poziom jasności jest równy jedności, oraz usuwania pojedynczych izolowanych pikseli, a dylatacja przeciwnie – do powiększania rozmiaru takich elementów. Przekształcenia te są addytywne i wpływają na zmianę całkowitej liczby pikseli o określonym poziomie jasności. Aby ograniczyć te efekty, erozję i dylatację stosuje się sekwencyjnie. Złożenie erozji, po której przeprowadzana jest dylatacja, nazywane jest otwarciem, a sekwencja odwrotna nazywana jest zamknięciem. Operacje otwarcia i zamknięcia są powszechnie używane do usuwania artefaktów i zakłóceń występujących w obrazach binarnych [518, 532, 607].
Wymienione przekształcenia morfologiczne, stanowią przykład operacji, które stosowane są w toku analizy obrazu. Możliwość ich łączenia pozwala na tworzenie złożonych sekwencji, które w wielu przypadkach pozwalają na automatyczne i w pełni powtarzalne przetwarzanie obrazu bez konieczności ingerencji ze strony operatora. Ma to szczególnie znaczenie w przypadku pracy z dużą liczbą cyfrowych obrazów zebranych w ustalonych warunkach pomiarowych. Umożliwia to utrzymanie stałego poziomu błędu dla wyznaczanych parametrów mikrostruktury w całej sekwencji obrazów i znacznie przyspiesza sam proces pozyskiwania informacji. Takie masowe przetwarzanie, a następnie analiza uzyskanych obrazów jest wykorzystywane w metodach rekonstrukcyjnych opisanych w kolejnych podrozdziałach, kiedy w trakcie obserwacji, zbierane i zapisywane są setki obrazów.
Klasyczne metody stereologiczne, opisane w podrozdziale 2.2, opierające się na pomiarach prowadzonych na losowych, dwuwymiarowych przekrojach, przez wiele dziesięcioleci stanowiły podstawowe narzędzie służące do badania i opisu budowy wewnętrznej materiałów. Wypracowane w ich ramach techniki pozyskiwania ilościowych parametrów mikrostruktury, dodatkowo rozwinięte dzięki wykorzystaniu cyfrowych obrazów, pozwoliły na sformułowanie wielu użytecznych relacji opisujących zależności między metodami wytwarzania materiałów ich mikrostrukturą i właściwościami (zob. rozdz. 1.3). Jednak wymienione już wcześniej ograniczenia, dotyczące głównie niejednoznaczności w określaniu kształtu cząstek, ale również krzywizny granic międzyziarnowych, czy nawet rozmiaru, powodują, że intensywnie rozwijane są metody badawcze, dostarczające bezpośrednich informacji o trójwymiarowej budowie materiału. Uzyskane na ich podstawie dane dotyczące mikrostruktury, pozwalają na zaawansowaną analizę cech morfologicznych i topologicznych w oparciu o nieobciążone estymatory [615–620] oraz stanowią podstawę do budowy modeli mikromechanicznych, dzięki którym opis najważniejszej relacji: wytwarzanie – mikrostruktura – właściwości, staje się bardziej kompletny i obiektywny.
Stosowane aktualnie metody trójwymiarowej rekonstrukcji mikrostruktury opierają się na trzech zasadniczo różnych koncepcjach [621]. Pierwsza grupa metod wykorzystuje dane doświadczalne, uzyskane bezpośrednio w trakcie pomiarów przeprowadzonych na rzeczywistym materiale. Metody należące do drugiej grupy, opierają się na symulacji procesów fizycznych, zachodzących podczas syntezy i obróbki modelowanego materiału. Natomiast grupa trzecia, to metody geometryczne. Koncentrują się one wyłącznie na morfologii ziaren, pomijając fizyczne podstawy procesu tworzenia mikrostruktury.
Biorąc pod uwagę trzy wymienione grupy, można zauważyć, że jedynie pierwsza z nich reprezentuje nurt metod doświadczalnych. Dane uzyskiwane aktualnie na podstawie pomiarów prowadzonych tymi metodami, pozwalają na dokładny opis i rekonstrukcję budowy wewnętrznej wielu materiałów [601, 621]. Niepewności pomiarowe, które są permanentną cechą wszystkich metod doświadczalnych, powodują jednak, że dokładność opisu jest ściśle uzależniona od właściwości analizowanego materiału. W przypadku wielu materiałów inżynierskich, przeprowadzenie rzetelnej rekonstrukcji mikrostruktury wymaga akwizycji oraz przetwarzania ogromnych ilości danych pomiarowych. Dlatego, poza kosztem samej aparatury pomiarowej, umożliwiającej rejestrację, przechowywanie i przetwarzanie danych, należy brać pod uwagę fakt, że badania tego typu są zwykle bardzo czasochłonne. Jeśli więc konieczna jest analiza dużej liczby wariantów mikrostruktury (np. podczas doboru albo optymalizacji metod syntezy materiału), lub gdy projektowany jest nowy materiał (który nie został jeszcze otrzymany), to możliwe jest jedynie wykorzystanie metod symulacyjnych albo geometrycznych.
Niezależnie jednak od przyjętej koncepcji, w każdej z wymienionych grup wypracowane zostały metody pozwalające na trójwymiarową rekonstrukcję mikrostruktury. W przypadku metod doświadczalnych, uzyskiwane są więc modele geometryczne, które pozwalają na szczegółową analizę kształtu, rozmiaru i rozkładu przestrzennego istotnych elementów mikrostruktury rzeczywistego materiału. Natomiast metody symulacyjne i geometryczne, zapewniają uzyskanie reprezentacji budowy materiału, statystycznie równoważnej rzeczywistej mikrostrukturze. Dodatkowo, pomimo fundamentalnych różnic, techniki wypracowane w każdej z grup mogą się wzajemnie uzupełniać. Często informacje uzyskane na podstawie pomiarów eksperymentalnych stanowią dane wejściowe dla metod symulacyjnych czy geometrycznych albo są podstawą do walidacji uzyskanych wyników. Z kolei techniki stosowane w metodach geometrycznych pozwalają na redukcję błędów w rekonstrukcji przeprowadzanej na podstawie danych pomiarowych oraz umożliwiają efektywną redukcję informacji opisujących morfologię ziaren, co pozwala na dalsze wykorzystanie takich modeli geometrycznych do symulacji numerycznych będących podstawą obliczeniowej inżynierii materiałowej.
Aby scharakteryzować budowę materiału polikrystalicznego z uwzględnieniem cech morfologicznych i topologicznych ziaren, ich orientacji krystalograficznej, oraz budowy granic międzyziarnowych, konieczne jest zaplanowanie i przeprowadzenie szczegółowych badań doświadczalnych. Dobór stosowanych w tym celu metod, uzależniony jest od właściwości rozpatrywanego materiału (faz składowych) i od rodzaju informacji jakie muszą zostać zarejestrowane. Czynnikami decydującymi są też wymiary próbki, czas potrzebny na zgromadzenie kompletnych danych doświadczalnych oraz sam rozmiar zebranych danych, który w przypadku pomiarów 3D jest znacznie większy w porównaniu do klasycznych metod stereologicznych. Dlatego pomimo szybkiego rozwoju technik służących do rejestracji danych, wzrostu mocy obliczeniowej komputerów, rozwoju oprogramowania do wizualizacji i analizy danych, czynniki te również mogą być decydujące przy wyborze metody.
Koncentrując się na jedno i wielofazowych polikryształach ceramicznych, można przyjąć, że wybór ogranicza się do metody przekrojów seryjnych i metod pochodnych oraz do tomografii komputerowej. Ograniczenie to wynika głównie z potrzeby obrazowania stosunkowo dużej objętości przestrzeni przy jednoczesnym zachowaniu wysokiej rozdzielczości. Jest to niezbędne do zapewnienia reprezentatywności próby, podczas badania obiektów o rozmiarach mikrometrów, a niekiedy nanometrów, jakimi są pojedyncze krystality czy granice je rozdzielające. Istotne jest również silne rozpraszanie, pochłanianie i odbijanie światła w zakresie widzialnym, występujące w tego typu materiałach, uniemożliwiające bezpośrednie zastosowanie technik mikroskopowych 3D (np. mikroskopii konfokalnej).
Na wstępie warto również zaznaczyć, że oprócz wielu różnic pomiarowych, które zostaną omówione w dalszej części, metoda przekrojów seryjnych i metody pochodne, należą do metod niszczących, a tomografia komputerowa do metod nieniszczących. W metodzie przekrojów seryjnych wymagana jest wstępna obróbka powierzchni: cięcie, polerowanie, a niekiedy trawienie, co w konsekwencji prowadzi do nieodwracalnego uszkodzenia próbki. Natomiast tomografia komputerowa oparta jest na transmisji promieniowania elektromagnetycznego, dlatego jest zasadniczo metodą nieniszczącą. Zatem różnice te mogą być istotne przy doborze metody, szczególnie w przypadku gdy w ramach prowadzonego eksperymentu mają być analizowane zmiany mikrostruktury zachodzące w trakcie badanego procesu.
Pozyskiwanie informacji o wewnętrznej budowie nieprzezroczystych ciał na podstawie skorelowanych płaskich przekrojów, jest wykorzystywane z powodzeniem od dawna w naukach biologicznych, medycznych i paleontologii [622–625]. Idea pomiaru opiera się na cyklicznie powtarzanej sekwencji, składającej się z dwóch kroków. W pierwszym, przygotowywana jest płaska powierzchnia próbki pozwalająca na przeprowadzenie obserwacji. Przy czym zakres niezbędnych w tym kroku czynności jest specyficzny dla badanego materiału oraz techniki rejestracji danych stosowanej w kroku kolejnym. Oprócz cięcia, może być więc wymagane polerowanie, ablacja, trawienie czy napylanie. Następnie, w kroku drugim, przy pomocy specyficznych technik obrazowania, z przygotowanej powierzchni zbierane są dane. Istotne jest, aby w trakcie całego eksperymentu utrzymać kontrolowaną (zwykle stałą) głębokość usuwania warstw w kolejnych powtórzeniach. Takie postępowanie pozwala na gromadzenie serii danych opisujących dwuwymiarowe przekroje badanego materiału z uwzględnieniem głębokości na jakiej zostały one pobrane (rys. 2.7).
Pierwsze próby wykorzystania tej metody do trójwymiarowego opisu mikrostruktury materiałów inżynierskich (metalicznych) zostały przeprowadzone i opisane przez Forsmana [626] już ponad 100 lat temu. Jednak szersze wykorzystanie nastąpiło dopiero w latach 90-tych ubiegłego wieku i było związane z rozwojem metod komputerowych, umożliwiających trójwymiarową rekonstrukcję mikrostruktury w postaci wirtualnych modeli 3D [627–629]. W połączeniu z automatyzacją etapu przygotowania przekrojów [522, 630–633] oraz zastosowaniem komputerowo wspomaganych metod przetwarzania i analizy cyfrowych obrazów [519, 555, 634, 635] doprowadziło to do gwałtownego rozwoju metody.
Aktualnie metoda przekrojów seryjnych (ang. serial sectioning) należy do podstawowych metod trójwymiarowej rekonstrukcji mikrostruktury stosowanych dla wielu materiałów (zob. tab. [tab:SerialSectioning]). Osiągalne tą metodą rozdzielczości zależą od wybranych technik przygotowania powierzchni i obrazowania. Klasyczna technika przekrojów seryjnych, oparta na szlifowaniu, polerowaniu i trawieniu powierzchni, w połączeniu z mikroskopią optyczną, pozwala na uzyskanie rozdzielczości na poziomie kilku mikrometrów [636]. Przy zastosowaniu w pełni automatycznych, sprzężonych systemów polerująco-trawiąco-rejestrujących, minimalna grubość warstwy może być mniejsza niż 0.1 μm (zob. rys. 2.12) [618, 637] i ograniczeniem jest tutaj rozdzielczość mikroskopii optycznej (\(\sim\)0.25 μm). Dla wielu materiałów taka dokładność odwzorowania jest zadowalająca. Przyjmuje się jednak, że zarejestrowane obrazy powinny posiadać rozdzielczość stanowiącą przynajmniej 1/10 wymiaru charakterystycznego dla najmniejszych badanych obiektów. W praktyce, dla materiałów polikrystalicznych, oznacza to możliwość badania mikrostruktury zawierającej ziarna o wymiarach nie mniejszych niż 1 μm [638].
Współcześnie projektowane i otrzymywane materiały ceramiczne, szczególnie z grupy ceramiki specjalnej i ceramicznych kompozytów ziarnistych, wymagają zastosowania znacznie większych rozdzielczości obrazowania. Krystality, czy ziarna fazy wtrąconej w kompozytach, posiadają często wymiary <100 nm [53, 152, 153]. Dodatkowo, trudności w przygotowaniu powierzchni, wynikające z dużej twardości, wydatnie wydłużają czas potrzebny do zebrania odpowiedniej liczby obrazów mogących posłużyć do rekonstrukcji. Z tych powodów, klasyczna metoda przekrojów seryjnych, nawet w połączeniu z pełną automatyzacją, nie rozpowszechniła się w zastosowaniu do materiałów ceramicznych.
Rozwinięciem klasycznej metody przekrojów seryjnych jest metoda, w której do usuwania kolejnych warstw materiału (frezowania powierzchni) wykorzystywana jest zogniskowana wiązka jonów (FIB, ang. Focused Ion Beam) [639–642]. Kolumna emitująca i kształtująca wiązkę – działo jonowe, może być częścią mikroskopu skaningowego, co pozwala na wykorzystanie jego optyki bezpośrednio do obrazowania powierzchni próbki [643, 644]. Komercyjne urządzenia dwukolumnowe (FIB-SEM) umożliwiają jednoczesne usuwanie materiału i obrazowanie. Pozwala to na całkowitą automatyzacje i znacząco przyspiesza cały proces oraz zwiększa dokładność i precyzję pozycjonowania rejestrowanych obrazów.
Kolejną zaletą płynącą z wykorzystania zogniskowanej wiązki jonów do frezowania powierzchni jest wszechstronność zastosowania. Metodę tę z powodzeniem stosuje się zarówno do stopów metali [609, 637, 645], materiałów ceramicznych [646–648], polimerów [649–651], a nawet do preparatów medycznych [652–654] czy biologicznych [655–657]. W porównaniu do typowych metod przygotowania powierzchni: cięcia, szlifowania i polerowania, wiązka jonów jest stosunkowo mało inwazyjna. W przypadku materiałów kruchych, zawierających dużą porowatość, oraz materiałów kompozytowych składających się z faz znacznie różniących się twardością, pozwala na zachowanie trudnych do preparatyki szczegółów mikrostruktury. Ponadto, grubość warstwy, w której występują uszkodzenia wywołane rozpylaniem jonowym, jest niewielka, co pozwala na zastosowanie dodatkowych trybów obrazowania powierzchni. Często stosowana jest więc technika wykorzystująca dyfrakcję elektronów wstecznie rozproszonych (EBSD), która dostarcza informacje o orientacji krystalograficznej oraz parametrach sieciowych [644, 658]. Stosowana jest również spektroskopia dyspersji energii promieniowania rentgenowskiego (EDS, ang. Energy Dispersive X-ray Spectroscopy), pozwalająca na analizę powierzchniową składu chemicznego i tym samym na identyfikację faz budujących materiał [646, 659].
Włączenie dodatkowych metod obrazowania nie tylko poszerza zasób informacji o analizowanym materiale, ale również pozwala na skuteczniejszą segmentację i indeksację elementów mikrostruktury w oparciu o różnorodny zestaw parametrów [654, 660]. Pomimo wydłużenia czasu niezbędnego na gromadzenie komplementarnych danych, dotyczących przykładowo orientacji krystalograficznej (EBSD [660–662]) czy składu chemicznego (EDS [646, 659]), w efekcie końcowym znacznie ułatwia to proces segmentacji, a nawet umożliwia zastosowanie w pełni zautomatyzowanych algorytmów segmentacji komputerowej, eliminując tym samym konieczność ingerencji człowieka w etap przetwarzania informacji [618, 654, 663].
Uzyskany techniką FIB-SEM trójwymiarowy opis cech morfologicznych, krystalograficznych i chemicznych, analizowanych elementów mikrostruktury, o rozmiarach nawet sub-mikronowych, charakteryzuje się wysoką wiernością obrazowania. Osiągane rozdzielczości przestrzenne sięgają 10 nm–15 nm (zob. rys. 2.12). Ograniczeniem jest tutaj grubość usuwanych warstw i ich liczba, co wiąże się z czasem potrzebnym do przeprowadzenia pomiaru [616, 664, 665]. Dlatego intensywnie rozwijane są nowe metody przygotowania powierzchni. Oprócz standardowo wykorzystywanych w tym celu jonów Galu, w działach jonowych używane są coraz częściej jony Helu, Neonu, Argonu, Ksenonu, ale także plazma oraz stosowane są rozwiązania sprzężone [637, 645, 666, 667] (zob. tab. [tab:SerialSectioning]). Znaczne przyspieszenie etapu przygotowania powierzchni uzyskuje się przy zastosowaniu ablacji laserowej, w której wykorzystuje się lasery femtosekundowe [637, 668–670].
Niewątpliwy postęp w rozwoju metody przekrojów seryjnych, który związany jest z zastosowaniem do obrazowania wysokorozdzielczych mikroskopów SEM i TEM w połączeniu z precyzyjnymi technikami przygotowania powierzchni, spowodował, że jest to jedna z coraz częściej stosowanych metod, pozwalających na trójwymiarową rekonstrukcję mikrostruktury. Oprócz rozdzielczości, która jest jednak ciągle zwiększana, główne ograniczenie wynika z samej koncepcji metody. Usuwanie kolejnych warstw materiału niszczy ,,źródło danych”, przez co niemożliwe są analizy dotyczące zmienności mikrostruktury w czasie. Ponadto zwiększenie rozdzielczości okupione jest ograniczeniem analizowanej objętości, co z kolei niekorzystnie wpływa na reprezentatywność uzyskiwanych danych.
W metodach opierających się na koncepcji przekrojów seryjnych, kluczowym etapem, pozwalającym uzyskać trójwymiarową, cyfrową reprezentację mikrostruktury, jest etap integracji zebranych danych. Uzyskane w trakcie akwizycji obrazy, zawierające, w zależności od zastosowanych technik obrazowania powierzchni, różnorodne dane, muszą zostać ze sobą przestrzennie połączone. Proces ten jest w istocie odwróceniem opisanych wcześniej kroków prowadzących do pozyskania danych. Pozwala on na odtworzenie wewnętrznej budowy próbki, ale nie w formie fizycznej, lecz w postaci wirtualnego, trójwymiarowego modelu. Zebrane obrazy, niezależnie od źródła (mikroskop optyczny, SEM, TEM), są więc układane w stos zgodnie z kolejnością, i co za tym idzie, głębokością \(z\), na jakiej zostały zarejestrowane (por. rys. 2.7). Następnie są wyrównywane względem siebie w płaszczyźnie rejestracji \(xy\). Etap ten istotnie wpływa na dokładność odwzorowania elementów mikrostruktury. Błędy systematyczne lub przypadkowe, wynikające z przesunięcia oraz obrotu próbki względem układu rejestrującego, powstające w kolejnych cyklach zbierania danych, muszą zostać w tym etapie skorygowane. Ma to szczególne znaczenie, gdy stosowane są techniki klasycznego usuwania warstw materiału poprzez polerowanie. Przekładanie próbki pomiędzy uchwytem polerki a stolikiem mikroskopu, powoduje nieuchronną zmianę jej pozycji w kolejnych cyklach akwizycji obrazu. Automatyzacja całego procesu znacznie zmniejsza tego typu błędy. Jednak nawet duża precyzja pozycjonowania próbki, sięgająca mikrometrów, jest niewystarczająca do celów rekonstrukcji. W mikroskopach dwuwiązkowych FIB-SEM, korekcja położenia może być realizowana już na etapie akwizycji obrazów, za pośrednictwem oprogramowania sterującego urządzeniem. W takim przypadku informacje o aktualnej pozycji zostają zapisane w postaci metadanych dołączanych do wynikowych obrazów.
Do korekcji położenia wykorzystuje się znaczniki odniesienia. W przypadku klasycznej techniki przekrojów seryjnych, powszechnie stosowana metoda opiera się na znakowaniu powierzchni próbki wgłębieniami wykonanymi przy pomocy twardościomierza [620, 643, 671, 672]. Znaczniki takie, będące wgłębieniami w czołowej powierzchni próbki, mają określony kształt zależny od zastosowanego narzędzia. Kształt ten nie zmienia się istotnie w trakcie usuwania kolejnych warstw materiału, natomiast rozmiary wgłębienia stopniowo maleją. Rejestracja takich znaczników na obrazach powierzchni pozwala na korekcję względnego położenia w płaszczyźnie \(xy\). Dodatkowo, analiza zmian wymiarów zarejestrowanych wgłębień w kolejnych cyklach, umożliwia korekcję położenia wzdłuż kierunku \(z\). Jest to szczególnie istotne dla technik wykorzystujących polerowanie powierzchni, gdzie grubość warstw wykazuje dużą zmienność. Natomiast przy zastosowaniu techniki wykorzystującej zogniskowaną wiązkę jonów, do znakowania wykorzystuje się działo jonowe, które nanosi charakterystyczne wzory, pozwalające zarówno na pozycjonowanie próbki w trakcie eksperymentu, jak również na późniejszą korekcję dryftu aparaturowego [640, 644, 660, 673, 674]. W przypadku eksperymentów trwających nierzadko wiele godzin czy nawet dni, uwzględnienie takiego dryftu wywołanego zmianami temperatury, drganiami czy wpływem innych czynników zewnętrznych, jest szczególnie istotne.
Kolejnym etapem prowadzącym do uzyskania trójwymiarowej rekonstrukcji mikrostruktury jest wstępne przetwarzanie zarejestrowanych obrazów. Ma ono na celu redukcję szumu, wyrównanie jasności pomiędzy kolejnymi obrazami w stosie, korekcję nierównomierności oświetlenia tła i inne operacje specyficzne zarówno dla zastosowanej metody akwizycji jak i dla analizowanego materiału (zob. p. 2.3). Podczas analizowania wielu zdjęć mikrostruktury – nierzadko setek – pomocne stają się skrypty, które w sposób wcześniej zaprogramowany (wsadowo) są w stanie automatycznie przetworzyć cały stos obrazów. Jednakże, jak wspomniono wcześniej, nie istnieje uniwersalna metoda przetwarzania obrazu i każdorazowo należy dostosować kolejne kroki do konkretnego przypadku mikrostruktury i zastosowanej metody obrazowania.
Tak przygotowany stos, składający się z wielu obrazów, zostaje następnie poddany segmentacji i interpolacji między płaszczyznami [616]. Kroki te mogą być realizowane w różnej kolejności, a niekiedy jednocześnie w oparciu o algorytmy sprzężone [663, 675–678]. Pozwala to na połączenie oddalonych od siebie (w kierunku \(z\)) dwuwymiarowych obrazów reprezentowanych przez macierz pikseli w trójwymiarowe obiekty składające się z wokseli (ang. Volumetric Picture Element). W najprostszej metodzie interpolacji wykorzystywana jest intensywność (poziomy jasności) pikseli, które usytuowane są w kolejnych, sąsiadujących ze sobą warstwach. Następnie, stosując funkcje interpolacyjne, ustalana jest intensywność dla wokseli wypełniających przestrzeń między warstwami [643, 665]. Metoda ta powoduje jednak rozmycie krawędzi rekonstruowanych elementów mikrostruktury, co może powodować błędy w segmentacji i niekorzystnie wpłynąć na dokładność. Alternatywną metodą jest interpolacja oparta na kształcie [619, 643, 679]. Wymaga ona identyfikacji krawędzi w dwuwymiarowych przekrojach, ale pozwala na dokładniejsze odwzorowanie kształtu elementów mikrostruktury.
Rozmiar utworzonych w ten sposób sześciennych wokseli, zależy zarówno od rozdzielczości wykorzystanych obrazów, jak i odległości między nimi w stosie. Najlepsze rezultaty rekonstrukcji osiągane są, gdy rozmiar pikseli jest zbliżony do odległości między płaszczyznami [616]. Ponieważ uzyskanie zadowalającej rozdzielczości obrazów, szczególnie przy zastosowaniu SEM czy TEM [619, 665, 680], jest zazwyczaj mniej czasochłonne niż usuwanie kolejnych warstw materiału, to głównie odległość między warstwami ogranicza końcową rozdzielczość przestrzenną rekonstrukcji [619, 680]. Dlatego na etapie przygotowania pomiarów, szacowana jest zwykle minimalną rozdzielczość przestrzenną niezbędną do osiągnięcia zakładanego celu rekonstrukcji – analizy mikrostruktury czy przygotowania modeli geometrycznych do symulacji numerycznych. Przyjmuje się, że do osiągnięcia zadowalającej dokładności odwzorowania, niezbędna jest rejestracja informacji pochodzących z co najmniej 10 przekrojów przypadających na rekonstruowany element. Takie oszacowanie rozdzielczości przestrzennej wymaga jednak przyjęcia a priori minimalnych rozmiarów istotnych elementów mikrostruktury. Lepszym podejściem jest zbadanie wpływu rozdzielczości przestrzennej na dokładność oszacowania analizowanych cech mikrostruktury [606, 681]. W przypadku rekonstrukcji mających na celu uzyskanie modeli geometrycznych służących do symulacji metodami przybliżonymi, należy rozpatrzyć również, jak duża szczegółowość odwzorowania jest rzeczywiście niezbędna do opisu modelowanego zjawiska. Przykładowo, stosując do analizy metodę elementów skończonych, nadmierne zwiększenie szczegółowości modelu powodujące duże zagęszczenie siatki, może utrudnić, lub wręcz uniemożliwić, przeprowadzenie symulacji.
W zależności od przyjętego toku rekonstrukcji, segmentacja może być prowadzona zarówno na stosie dwuwymiarowych obrazów mikrostruktury, jak i na uzyskanej podczas interpolacji trójwymiarowej macierz wokseli. W najprostszym przypadku, wykorzystywane są informacje pochodzące z jednego źródła akwizycji i segmentacja polega na grupowaniu pikseli bądź wokseli o jednakowych (albo zbliżonych) wartościach intensywności, technikami wykorzystywanymi przy ilościowej analizie obrazu (zob. rozdz. 2.3). Prowadzi to do podziału analizowanej przestrzeni na obiekty reprezentujące wybrane elementy mikrostruktury rekonstruowanego materiału. Coraz częściej do segmentacji wykorzystywane są jednak równocześnie informacje zarejestrowane różnymi technikami [637, 673, 682, 683], a uzyskane w ten sposób rekonstrukcje poddawane są dodatkowym operacjom mającym na celu uzupełnienie brakujących informacji strukturalnych oraz usunięcie artefaktów i wygładzenie powierzchni zrekonstruowanych elementów mikrostruktury [644, 663, 678, 681]. Wykorzystywane są w tym celu metody symulacyjne (MC) i teselacyjne [654, 676, 678] (zob. p. 2.6).
Tomografia komputerowa (CT, ang. Computed Tomography) jest metodą polegającą na odwzorowywaniu wewnętrznej, trójwymiarowej budowy na podstawie serii dwuwymiarowych projekcji, uzyskiwanych przy pomocy promieniowania rentgenowskiego, przepuszczanego przez badany obiekt pod różnymi kątami. Co do zasady, jest więc metodą nieniszczącą. Matematyczne podstawy zostały opisane ponad 100 lat temu przez Radona [684]. W latach 60-tych Cormack [685] rozwinął je i wykonał pierwszy testowy eksperyment, z myślą o wykorzystaniu metody do trójwymiarowego obrazowania na potrzeby radiologii. Już kilka lat później powstał komercyjny skaner rentgenowski do tomografii komputerowej zbudowany w laboratoriach EMI przez Hounsfielda [686]. Za prace te w 1979 Cormack i Hounsfield otrzymali nagrodę Nobla z medycyny.
Pierwotnie budowane tomografy rentgenowskie dostosowane były do zastosowań medycznych. Wymagało to używania możliwie niskich dawek promieniowania oraz krótkiego czasu gromadzenia danych. Jednak już w latach 80-tych, zauważono potencjał metody również w innych dziedzinach nauki oraz techniki [687–691]. Zmodyfikowane urządzenia, w których zastosowano wysokorozdzielcze detektory oraz źródła promieniowania o większej energii, umożliwiły uzyskanie rekonstrukcji z rozdzielczością przestrzenną poniżej 20 μm. Tym samym techniki te przyjęto nazywać mikrotomografią komputerową (\(\mu\)-CT) i stały się narzędziem pozwalającym na nieniszczące badania budowy wewnętrznej materiałów.
Aktualnie, w tomografii komputerowej, stosowane są zarówno laboratoryjne, jak i synchrotronowe źródła promieniowania. Pozwala to na pokrycie szerokiego zakresu energii: od promieniowania miękkiego – poniżej 1 keV, do twardego – nawet powyżej 100 keV. Urządzenia laboratoryjne, w których wiązka rentgenowska jest rozbieżna i polichromatyczna, uzyskują zwykle rozdzielczość przestrzenną od kilku milimetrów do jednego mikrometra, przy czasie akwizycji wynoszącym 15 minut–30 minut. Natomiast stosując synchrotronowe źródła promieniowania, w których wiązka jest równoległa (polichromatyczna lub monochromatyczna), typowa rozdzielczość przestrzenna wynosi od 40 do 0.5 μm, przy czasie akwizycji rzędu kilku minut lub krótszym [692]. W niektórych eksperymentach udaje się uzyskać jeszcze większe rozdzielczości, sięgające nawet poniżej 100 nm (nano-CT) [693–696].
Rozdzielczość rekonstrukcji zależy jednak nie tylko od zastosowanego źródła (energii i natężenia fotonów) oraz czasu akwizycji pojedynczych projekcji. Istotny jest również układ optyczny i detektor. Najczęściej do rejestracji natężenia promieniowania przechodzącego przez badaną próbkę stosuje się matrycowe detektory promieniowania, których fizyczna rozdzielczość (liczba komórek, pikseli) ogranicza liczbę rekonstruowanych wokseli (ang. Volumetric Picture Element, Voxel). Innymi słowy, wraz ze wzrostem wymaganej rozdzielczości obrazowania, maleje objętość przestrzeni dla której zbierane są dwuwymiarowe projekcje. Ograniczenie to udaje się ominąć rozszerzając pole widzenia tomografu poprzez połączenie ze sobą projekcji wykonanych dla sąsiadujących obszarów [697, 698].
Zastosowanie szybkich detektorów matrycowych w połączeniu z jasnymi synchrotronowymi źródłami fotonów, pozwala również na rejestrację zmian w badanym obiekcie zachodzących w czasie eksperymentu. Czterowymiarowe modele (4D), uzyskiwane metodą \(\mu\)-CT, opisujące nie tylko wymiary przestrzenne elementów budowy materiału (3D), ale również ich ewolucję w czasie, zaczynają być coraz częściej wykorzystywane w inżynierii materiałowej. W ten sposób badane są procesy krzepnięcia stopów metali i rekrystalizacji [699–703], zjawiska sprężyste, plastyczne [698, 704–706], zjawiska zmęczeniowe oraz rozwój mikropęknięć [707–709], metalurgia proszków, spiekanie [710], procesy geologiczne oraz mineralogiczne [711–714] i wiele innych.
Fizyczne podstawy tomografii komputerowej opierają się na osłabieniu intensywności promieniowania przechodzącego przez badaną próbkę i, tak jak w przypadku innych metod spektroskopowych [715], zjawisko to można opisać prawem Lamberta–Beera, które dla ośrodków jednorodnych przyjmuje postać [715]: \[\label{eq:L-B} I = I_0 \mathop{\mathrm{e}}^{-\mu L}\!,\] przy czym \(I_0\) wyraża natężenie promieniowania padającego, \(I\) natężenie promieniowania przechodzącego przez ośrodek na drodze \(L\), a \(\mu\) jest liniowym współczynnikiem osłabienia. Współczynnik ten ujmuje sumę efektów wywołanych pochłanianiem energii w wyniku efektu fotoelektrycznego, rozpraszania komptonowskiego i kreacji par elektron-pozyton. W zakresie energii promieniowania rentgenowskiego stosowanego w \(\mu\)-CT, absorpcja zdominowana jest przez efekt fotoelektryczny, który zależy od energii promieniowania \(E\) oraz właściwości substancji pochłaniającej: gęstości \(\rho\) oraz liczby atomowej \(Z\). Zależność tę można przedstawić empirycznym równaniem [715]: \[\label{eq:mi} \frac{\mu}{\rho} = k \frac{Z^4}{E^3},\] w którym \(k\) jest wartością stałą przy określonych warunkach pomiaru, a stosunek \(\mu/\rho\) nazywany jest masowym współczynnikiem osłabienia.
Z powyższego równania wynikają istotne wnioski dotyczące kontrastu absorpcyjnego, będącego ważnym parametrem decydującym o możliwości zastosowania metody do rekonstrukcji wybranych materiałów inżynierskich. Kontrast absorpcyjny, pozwalający na segmentację elementów składowych analizowanego obiektu, zależy głównie od liczby atomowej (\(Z^4\)). Dlatego metoda ta może być z powodzeniem stosowana do analizowania budowy wewnętrznej materiałów kompozytowych, betonów oraz skał [698, 704, 714, 716–718]. Różnice w gęstości pomiędzy fazami składowymi, dodatkowo zwiększające kontrast absorpcyjny, powodują, że \(\mu\)-CT jest również często wykorzystywana w przypadku materiałów o wysokiej porowatości: materiałów komórkowych i stałych pian [705, 712, 719, 720], ale także w defektoskopii, fraktografii, kontroli materiałów wytwarzanych addytywnie (druk 3D) oraz w zastosowaniach przemysłowych do kontroli jakości [690, 691, 708, 721–723].
Głównym atutem metody jest jednak możliwość trójwymiarowej rekonstrukcji budowy wewnętrznej materiału, na podstawie przetworzonych informacji zarejestrowanych w postaci dwuwymiarowych projekcji. Wykorzystywane w tym celu algorytmy opierają się na transformacji Radona, która pozwala rozwikłać rejestrowany spadek intensywności promieniowania.
Rozpatrując osłabienie wiązki przechodzącej przez niejednorodną próbkę, dla dwuwymiarowego jej przekroju, w którym kierunek \(x\) jest prostopadły do kierunku przenikania wiązki, a kierunek \(y\) do niej równoległy, równanie \eqref{eq:L-B}, można przedstawić w formie logarytmicznej [724]: \[\label{eq:log_hetero_L-B} \ln \left[\frac{I_0}{I(x)}\right] = P\left( x \right) = \int\limits_{0}^{L} \mu(x,y)\mathop{}\!\mathrm{d}{}y.\] W równaniu tym \(\mu(x,y)\) jest funkcją przedstawiającą dwuwymiarowy rozkład współczynników osłabienia, i tym samym opisującą budowę wewnętrzną badanego materiału, natomiast \(\ln \left[{I_0}/{I(x)}\right]\) jest rejestrowaną projekcją \(P\left( x \right)\), czyli rozkładem przestrzennym zmian intensywności sygnału docierającego do detektora, wynikających z przejścia promieniowania przez niejednorodny materiał na drodze \(L\).
W celu pełnej rekonstrukcji – zgodnie z twierdzeniem Radona [684] – należałoby zarejestrować nieskończenie wiele takich projekcji, ale praktycznie ich liczba mieści się zwykle w zakresie od kilkuset do kilku tysięcy. Ponieważ projekcje rejestrowane są pod różnymi kątami \(\theta\) względem próbki, to wygodnie jest posługiwać się biegunowym układem współrzędnych. Oprócz kąta, w takim układzie, projekcja charakteryzowana jest współrzędną \(t\), określającą odległość na osi równoległej do detektora (rys. 2.8).
Wykorzystując współrzędne pomiarowe (\(\theta\) i \(t\)), równanie \eqref{eq:log_hetero_L-B} opisujące gromadzone w trakcie eksperymentu projekcje, można zatem zapisać w postaci [725]: \[\label{eq:projekcja} P_\theta \left( t \right) = \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} \mu(x,y)\, \delta \left( x \cos \theta + y \sin \theta - t \right) \mathop{}\!\mathrm{d}{}x \mathop{}\!\mathrm{d}{}y.\] Równanie to nazywane jest Transformatą Radona i w ujęciu matematycznym, wyraża ono transformację dokonywaną przez fizyczny układ, przy pomocy promieniowania przechodzącego przez próbkę, dwuwymiarowej funkcji \(\mu \left( x,y \right)\) opisującej jej budowę wewnętrzną, na rejestrowane przez detektor projekcje \(P_{\theta} \left( t \right)\).
W powyższym opisie, matematycznych i fizycznych podstaw metody, założono, że promieniowanie wykorzystywane do rejestracji danych jest monochromatyczne, a wiązka jest skolimowana. Warunki takie nie muszą być jednak spełnione i w zależności od rodzaju źródła promieniowania oraz rozwiązań technicznych, zastosowanych w konkretnym urządzeniu, opis musi zostać rozbudowany [724–728].
Niezależnie od parametrów technicznych, podstawą do odtworzenia budowy wewnętrznej materiału przy pomocy CT, jest zarejestrowany zbiór projekcji. Ich dyskretny charakter, wynikający ze skończonej liczby kątów, pod którymi są one zbierane, jak i z konstrukcji detektorów, powoduje, że do rekonstrukcji nie wykorzystuje się bezpośrednio odwrotnej Transformaty Radona. W takich warunkach efektywniejsze stają się algorytmy oparte na wstecznej projekcji (BP, ang. Back Projection), którą można przedstawić równaniem [728]: \[\label{eq:backproj} \tilde{\mu}(x,y) = \int\limits_{0}^{\pi} P\left( x \cos \theta + y \sin \theta , \theta \right) \mathop{}\!\mathrm{d}{}\theta\] Tak zdefiniowana wsteczna projekcja, przypisuje każdemu punktowi w przestrzeni przekroju \((x,y)\) sumę wartości funkcji projekcji \(P\) zebranych dla wszystkich kątów \(\theta\) w punkcie o współrzędnej biegunowej \(t\) (zapisanej jako \(x \cos \theta + y \sin \theta\)). Należy jednak zauważyć, że uzyskany w ten sposób rozkład współczynnika osłabienia \(\tilde{\mu}(x,y)\) nie jest tożsamy z rzeczywistym rozkładem \(\mu(x,y)\) w badanej próbce. Wsteczna projekcja powoduje, że zrekonstruowany \(\tilde{\mu}(x,y)\) oprócz informacji o oryginalnym kształcie funkcji rozkładu współczynnika osłabienia, zawiera również zniekształcenia geometryczne. Powstające w ten sposób artefakty zazwyczaj utrudniają, a często wręcz uniemożliwiają, bezpośrednią interpretację i dalszą segmentację zrekonstruowanego obrazu.
Aby zilustrować opisany problem można posłużyć się przykładem rekonstrukcji syntetycznego przekroju przedstawionym na rysunku 2.9. W celu uzyskania projekcji, testowy obraz przekroju (rys. 2.9a) poddany został transformacji Radona dla wybranej liczby kątów \(\theta\) (od 2 do 256). Następnie metodą BP, wykorzystując 2, 16 i 256 projekcji, zrekonstruowany został obraz testowy (kolejno rys. 2.9b, 2.9c i 2.9d).

Przy dużej liczbie projekcji wykorzystywanych do rekonstrukcji metodą BP, pojawia się silne rozmycie krawędzi elementów składowych przekroju. Zniekształcenia takie mogą być jednak skutecznie filtrowane. Najczęściej stosuje się w tym celu wstępną filtrację kolejno zbieranych projekcji i dopiero na podstawie tak przygotowanych danych dokonuje się rekonstrukcji metodą wstecznej projekcji. Rysunek 2.9 (e-g) przedstawia rekonstrukcje syntetycznego przekroju (rys. 2.9a), wykonane analogicznie do wcześniejszego przykładu, jednak wykorzystane projekcje zostały wstępnie poddane filtracji w dziedzinie częstotliwości przy pomocy filtru Ram-Lak (Ramachandran, Lakshminarayanan [729]). Dzięki tak przeprowadzonej rekonstrukcji uzyskany z wykorzystaniem 256 filtrowanych projekcji przekrój (rys. 2.9g) nie wykazuje już tak silnego rozmycia. Przykład ten potwierdza efektywność metody wstecznej projekcji z filtrowaniem, która stała się punktem wyjścia dla całej klasy analitycznych algorytmów rekonstrukcyjnych, wykorzystujących zarówno transformatę Fouriera, konwolucję jak i szereg specjalistycznych filtrów (ang. Convolution/Filtration Back-Projection, Fourier-Based Reconstruction Methods) [724–728].
W tomografii komputerowej, oprócz metod analitycznych, stosowane są również algebraiczne techniki rekonstrukcyjne (ART, ang. Algebraic Reconstruction Techniques). Podstawy matematyczne, które wykorzystywane są w tych technikach zostały opisane przez Kaczmarza [730] na wiele lat przed pojawieniem się pierwszych tomografów i dotyczyły problemu przybliżonego rozwiązywania układów równań liniowych metodą iteracyjną. Idea ART opiera się na założeniu, że rekonstruowany obraz składa się ze skończonej liczby komórek o jednakowych wymiarach. Elementy te są określone przez współrzędne położenia na przekroju (\(x\) i \(y\)) oraz posiadają stałą wartość współczynnika osłabienia (\(\hat{\mu}(x,y)\)). Dodatkowo w technikach ART przyjmuje się, że promień przechodzący przez materiał ma skończoną grubość (\(\tau\)), zwykle równą rozmiarowi komórek (rys. 2.10). Rejestrowaną dla takiego pojedynczego promienia dyskretną składową projekcji \(p_i\), można więc przedstawić jako sumę: \[\label{eq:ARTsum} p_i = \sum\limits_{j=1}^{N} w_{ij} f_j\] w której \(f_j\) reprezentuje wartość współczynnika osłabienia \(\hat{\mu}(x,y)\) dla \(j\)-tej spośród \(N\) komórek, a \(w_{ij}\) jest współczynnikiem wagowym, określającym wkład \(j\)-tej komórki do całkowitej wartości składowej projekcji \(p_i\) dla \(i\)-tego promienia. Wartość współczynnika \(w_{ij}\) jest równa udziałowi powierzchniowemu tej części komórki, którą pokrywa przechodzący przez nią \(i\)-ty spośród \(M\) promieni (rys. 2.10).
Wyznaczenie wszystkich wartości \(f\), a tym samym zrekonstruowanie rozkładu współczynnika osłabienia w rozpatrywanej płaszczyźnie, jest możliwe poprzez rozwiązanie układu równań składającego się z \(M\) równań \eqref{eq:ARTsum}. Z powodów praktycznych, wynikających z rozmiaru macierzy \(w_{ij}\) (\(M \times N\), przy czym dla obrazów o wymiarach 1024 x~1024 px, \(N = 1024^2\), a \(M\) – w zależności od zastosowanej techniki – może być równe \(N\)), konwencjonalne metody są tutaj nieefektywne. Dlatego wykorzystywane są do tego celu metody iteracyjne, bazujące na wspomnianej już pracy Kaczmarza [730] oraz późniejszej Tanabe [731].
Algorytmy wykorzystujące ART, jak również te, oparte na metodzie analitycznej – stosujące odwrotną Transformatę Radona czy wsteczną projekcję w połączeniu z filtrowaniem – zasadniczo różnią się między sobą wymaganiami dotyczącymi układu pomiarowego, sposobu akwizycji danych i ich ilości, niezbędnej do przeprowadzenia rekonstrukcji. Różnice dotyczą również szybkości oraz wierności odwzorowania budowy wewnętrznej analizowanej próbki. W związku z tym, kryteria doboru metody związane są zarówno z konstrukcją układu pomiarowego (rodzajem tomografu), jak również z oczekiwanymi rezultatami dla konkretnego zagadnienia (dokładnością i skalą rekonstrukcji materiału, rejestracją zmian próbki w czasie, itp.) [732].
Opisane do tej pory zagadnienia leżące u podstaw tomografii komputerowej, opierają się na kontraście absorpcyjnym, występującym pomiędzy elementami składowymi ciała. W przypadku \(\mu\)-CT, gdy analizowane są materiały wielofazowe, kontrast ten nazywany jest wprost – kontrastem fazowym, a tomografia wykorzystująca współczynnik osłabienia – tomografią kontrastu fazowego (ang. phase contrast tomography). Stała wartość współczynnika osłabienia w obrębie faz składowych, wynikająca z określonego ich składu chemicznego oraz budowy przestrzennej (co ujmuje równianie \eqref{eq:mi}), pozwala na skuteczną segmentację i, jak już wcześniej wspomniano, na wystarczająco szczegółową analizę wielu różnorodnych materiałów. W przypadku materiałów polikrystalicznych, zarówno metalicznych jak i ceramicznych, do pełnego opisu mikrostruktury niezbędne są jednak dodatkowe informacje, dotyczące kształtu i rozmieszczenia pojedynczych krystalitów. Cechy te pozostają ukryte dla tomografii kontrastu fazowego. Jeśli jednak spełniony jest warunek Braggów29, to promieniowanie rentgenowskie przechodzące przez materiał polikrystaliczny ulega również dyfrakcji. Stosując zatem jasne, monochromatyczne źródła twardego promieniowania rentgenowskiego (źródła synchrotronowe) można dodatkowo obserwować kontrast dyfrakcyjny, wynikający z różnego kąta ugięcia wiązki na płaszczyznach sieciowych przypadkowo zorientowanych krystalitów [733–735].
Pierwszą techniką tomograficzną, w której wykorzystano kontrast dyfrakcyjny, była trójwymiarowa mikroskopia dyfrakcji rentgenowskiej (3DXRD, ang. Three-Dimensional X-Ray Diffraction) [736–738]. Podobnie jak w przypadku tomografii kontrastu fazowego, w 3DXRD stosuje się detektor umieszczony za próbką. Rejestruje on jednak projekcje składające się z plamek dyfrakcyjnych pochodzących od krystalitów, dla których, przy określonej orientacji próbki względem wiązki, spełniony jest warunek Braggów (rys. 2.11). Indeksacja zarejestrowanych plamek pozwala na śledzenie zmian ich kształtu i położenia względem osi wiązki, wynikających z obrotu próbki w trakcie pomiaru. Umożliwia to niezależną rekonstrukcję kształtu pojedynczych krystalitów. Istotna w tej technice jest również odległość detektora od próbki. Detektor umieszczony w odległości kilku milimetrów, wyposażony w matrycę o niewielkich rozmiarach piksela (\(\sim\)2 μm) – detektor bliskiego pola (ang. near field detector) [739], pozwala rejestrować szczegółowe informacje o kształcie krystalitów, jednak wyznaczenie ich orientacji krystalograficznej, oparte na pomiarze kąta \(2\theta\), obarczone jest w tych warunkach dużym błędem. Natomiast detektor oddalony o kilkadziesiąt, czy nawet kilkaset centymetrów od powierzchni próbki, posiadający matrycę o dużym rozmiarze pikseli (> 50 μm) – detektor dalekiego pola (ang. far field detector) [739], rejestruje wartości uśrednione. Umożliwia to precyzyjny pomiar kąta \(2\theta\) i tym samym określenie orientacji poszczególnych krystalitów. Dodatkowo, w takim układzie, możliwe są pomiary odkształceń sieci krystalicznej i średnich naprężeń w krystalitach [740, 741], ale z uwagi na rozmiary pikseli i dużą odległość detektora od próbki, tracone są informacje pozwalające na rekonstrukcję kształtu. Aby jednocześnie rejestrować dane zarówno z bliskiego jak i dalekiego pola wykorzystywane są półprzezroczyste detektory ustawione kolejno za sobą [739, 742].
Stosowane aktualnie rozwiązania różnią się jednak nie tylko odległością między próbką a detektorem oraz ich rozdzielczością, ale również kształtem wiązki promieniowania [744]. W klasycznej technice 3DXRD stosowane są wiązki równoległe (ang. pencil beam) [739]. Jednak w zależności od źródła promieniowania oraz kolimatora (układu przesłon) można uzyskać również płaskie, liniowe wiązki. Taki kształt wiązki wykorzystywany jest w mikroskopii dyfrakcji promieniowania wysokiej energii (HEDM, ang. High Energy Diffraction Microscopy) [741, 745–747]. Rejestracja danych następuje tutaj sekwencyjnie – warstwa po warstwie. Pozwala to na precyzyjną rekonstrukcję budowy wewnętrznej ale okupione jest długim czasem akwizycji [741].
Inne rozwiązanie stosowane jest w tomografii kontrastu dyfrakcyjnego (DCT, ang. Diffraction Contrast Tomography). Kolimator formuje szerokokątną wiązkę, która po przejściu przez próbkę trafia na wysokorozdzielczy detektor rejestrujący jednocześnie kontrast fazowy i projekcje ziaren, dla których spełniony jest warunek dyfrakcji Braggów (rys. 2.11) [748, 749]. Dzięki takiemu rozwiązaniu, wydatnie skraca się czas skanowania, jednak zmniejszeniu ulega liczba rejestrowanych danych strukturalnych [741, 744].
Z wymienionymi technikami rejestracji danych strukturalnych i mikrostrukturalnych związane są specyficzne strategie rekonstrukcyjne. W zależności od właściwości badanego materiału, zmienności orientacji krystalograficznej elementów składowych oraz zakładanego celu prowadzonych pomiarów, można wyróżnić kilka typowych sposobów postępowania [739, 743, 744, 750, 751]. W pierwszym z nich rekonstrukcja kształtu ziaren (3D) opiera się zazwyczaj na danych pochodzących z detektora dalekiego pola i jest zredukowana do klasycznego problemu rekonstrukcji obrazu na podstawie projekcji. Wykorzystywane są w tym celu opisane już klasyczne algorytmy CT. Sposób ten może być zastosowany dla materiałów, w których zmienność orientacji elementów składowych materiału (krystalitów) jest niewielka i wystarczy przybliżona rekonstrukcja, ograniczona jedynie do ziaren wybranej fazy. Takie rozwiązanie zawodzi jednak w przypadku bardziej skomplikowanej mikrostruktury.
Jeśli podczas akwizycji rejestrowany jest bardziej rozbudowany zestaw danych, to możliwe jest określenie pozycji i objętości poszczególnych ziaren oraz ich uśrednionej orientacji. Na tej podstawie, stosując metody geometryczne (teselację, zob. p. 2.6.4), zrekonstruowana może zostać przybliżona mikrostruktura materiałów polikrystalicznych zawierających ziarna o rozmiarze przekraczającym kilka mikrometrów [744, 752].
Zastosowanie zestawu wysokorozdzielczych detektorów pozwala na pełną rekonstrukcję budowy wewnętrznej, na poziomie poszczególnych krystalitów. W takim przypadku stosowane są algorytmy ,,projekcji w przód” (ang. forward projection), w których dla kolejnych wokseli dobierane są orientacje odpowiadające zarejestrowanym wzorcom dyfrakcyjnym. Możliwe jest w tym wypadku również zastosowanie algorytmów CT (opartych na ART), w których na podstawie różnic w gęstości pomiędzy ziarnami a graniami międzyziarnowymi, ustalany jest próg segmentacji [739]. Z uwagi na bardzo duży rozmiar danych zbieranych przy wykorzystaniu wysokorozdzielczych detektorów, stosowane są również metody sprzężone opierające się zarówno na technikach rekonstrukcyjnych CT jaki i na technikach symulacyjnych oraz geometrycznych [739, 743, 751, 753, 754].
Opisane metody doświadczalne w ostatnim dziesięcioleciu osiągnęły poziom pozwalający na precyzyjne odwzorowanie budowy wewnętrznej dla wielu materiałów w tym również materiałów ceramicznych [621, 648, 732, 755]. Rekonstruowane na podstawie danych pomiarowych trójwymiarowe modele geometryczne, cechuje wysoka szczegółowość, umożliwiająca bezpośrednie wyznaczenie wielu parametrów morfologicznych i topologicznych, opisujących mikrostrukturę badanych materiałów. Jednym z głównych ograniczeń w rozwoju badań nad budową wewnętrzną, jest więc dziś głównie dostępność aparatury pomiarowej.
W przypadku metod wywodzących się z koncepcji przekrojów seryjnych w szczególności FIB-SEM istotnym czynnikiem jest stosunkowo długi czas pomiaru, który niekorzystnie wpływa na liczbę przeprowadzanych badań. Ponadto błędy na etapie segmentacji, wynikające zarówno z kwestii technicznych związanych z pozycjonowaniem próbki czy frezowaniem powierzchni [654, 660, 664, 667] jak i z właściwości analizowanego materiału, mogą znacząco skomplikować proces rekonstrukcji (przetwarzania końcowego). Wykorzystanie dodatkowych trybów obrazowania powierzchni pozwala poprawić dokładność i niezawodność wykorzystywanych algorytmów jednak wydłuża czas niezbędny na przeprowadzenie pomiaru, analizę obrazu i końcową rekonstrukcję mikrostruktury [654, 660, 664, 756, 757].
W badaniach materiałowych wykorzystujących techniki tomografii komputerowej, niezbędne są źródła promieniowania o energii znacznie większej niż w przypadku analizy polimerów, preparatów biologicznych czy w diagnostyce medycznej. Laboratoryjne źródła promieniowania nie pozwalają na uzyskanie wymaganej jasność i intensywność wiązki, dlatego do pomiarów wymagających dużej rozdzielczości, zapewniającej dokładne odwzorowanie budowy elementów o wymiarach sub-mikronowych, wykorzystywane są źródła synchrotronowe. Wiąże się to jednak lokalizacją laboratoriów pomiarowych przy centrach badawczych posiadających akceleratory cząstek. Odpowiednie linie badawcze, posiadające stanowiska umożliwiające przeprowadzenie niezbędnych pomiarów, skupione są aktualnie tylko w kilkunastu ośrodkach na świecie [758–764]. Takie ograniczenie powoduje, że zapotrzebowanie na pomiary tomograficzne znacznie przerasta możliwości pomiarowe tych laboratoriów [765].
W podsumowaniu metod doświadczalnych należy również wspomnieć o innych metodach wykorzystywanych do rekonstrukcji materiałów w skali sub-nanometrycznej, a nawet atomowej. Należy do nich tomografia elektronowa (ET, ang. Electron Tomography), w której do obrazowania wykorzystywana jest transmisyjna mikroskopia elektronową oraz skaningowa transmisyjna mikroskopia elektronowa (STEM). Uzyskiwanie tą metodą rozdzielczości przestrzenne sięgają 1 nm3 [609, 766, 767]. Jeszcze większą rozdzielczość dochodzącą do 0.2 nm zapewnia tomografia sondy atomowej (APT, ang. Atom Probe Tomography) [768, 769]. Ponieważ w metodach tych objętość rekonstruowanej przestrzeni jest niewielka, to mają one zastosowanie głównie do analizy budowy nanomateriałów [609, 621].
Zwiększanie rozdzielczości obrazowania, a tym samym szczegółowości trójwymiarowych rekonstrukcji mikrostruktury, zapewnia coraz precyzyjniejszy opis wewnętrznej budowy materiałów. Trójwymiarowe modele geometryczne, będące cyfrową reprezentacją mikrostruktury, wykorzystywane do analizy ilościowej oraz stanowiące podstawą modeli obliczeniowych, muszą jednak opisywać reprezentatywną objętość materiału. Uzyskanie pożądanej rozdzielczości przy jednoczesnym zachowaniu wystarczająco dużej objętości, spełniającej warunek reprezentatywności, jest w praktyce często trudne do osiągnięcia. Na rysunku 2.12 przedstawione zostały zakresy rozdzielczości i objętości, możliwe do osiągnięcia przy pomocy najważniejszych metod obrazowania w 3D. W przypadku materiałów polikrystalicznych, zróżnicowanie rozmiaru i kształtu krystalitów sprawia, że statystycznie istotne wyniki można uzyskać opierając się na próbie składającej się z co najmniej kilkuset, a zazwyczaj kilku tysięcy elementów [771]. Przyjęcie takiego reżimu wymaga zebrania danych, których liczebność, reprezentowana wymiarami macierzy wokseli, przekracza 1000^3 [637, 770] (rys. 2.12). Powoduje to również znaczące wydłużenie czasu rejestracji danych i w efekcie wprowadza dodatkowe ograniczenia przy wyborze metody pomiarowej [765].
Metody symulacyjne i geometryczne to metody pozwalające na uzyskanie syntetycznej mikrostruktury materiału. W zależności od celu rekonstrukcji, taka mikrostruktura może być statystycznie równoważna rzeczywistej, albo może opisywać wirtualny materiał, będący wynikiem eksperymentów in silico 49. W odróżnieniu od metod doświadczalnych, w których cyfrowa reprezentacja mikrostruktury jest uzyskiwana wyłącznie na podstawie danych pomiarowych, w metodach symulacyjnych i geometrycznych dane takie mogą stanowić uzupełnienie, ale nie są niezbędne do uzyskania syntetycznej mikrostruktury. Te fundamentalne różnice w sposobie rekonstrukcji powodują, że uzyskiwany opis budowy wewnętrznej materiału, pozbawiony jest ograniczeń typowych dla metod doświadczalnych. Błędy segmentacji, ograniczona ilość zebranych danych oraz artefakty powstałe w trakcie przetwarzania danych pomiarowych mogą sprawiać, że model geometryczny uzyskany metodami doświadczalnymi wymaga dodatkowych korekcji [678, 772]. Bezpośrednie wykorzystanie takich modeli do symulacji numerycznych, powoduje również nadmierną złożoność modeli obliczeniowych, wynikającą z obecności wielu szczegółów budowy, które mogą być nieistotne przy analizie rozpatrywanych zjawisk [679, 773, 774]. Dlatego metody symulacyjne i geometryczne stosowane są również na etapie przetwarzania danych doświadczalnych i pozwalają skorygować albo uprościć opis budowy materiału, co umożliwia efektywniejszą analizę uzyskiwanych informacji [678, 775, 776].
W ostatnich kilkunastu latach przedstawionych zostało szereg koncepcji i opracowano wiele algorytmów, wpisujących się w zakres metod symulacyjnych i geometrycznych [601, 621, 774]. W dalszej części podrozdziału, zostaną omówione więc wybrane rozwiązania, mające zastosowanie do rekonstrukcji mikrostruktury jedno- i wielofazowych materiałów polikrystalicznych.
Określenie in silico (w krzemie), jest stosowane do ogólnego ujęcia wszystkich metod badawczych prowadzonych przy pomocy komputerów (metod numerycznych) i zostało wprowadzone przez analogię do określeń in vivo i in vitro.↩︎
Koncepcja automatów komórkowych (CA, ang. Cellular Automata) powstała w na przełomie lat 40. i 50. ubiegłego stulecia i jej autorami byli Ulam i von Neumann [777]. W drugiej połowie XX wieku, wraz z rozwojem komputerów, koncepcja ta stała się podstawą wielu prac teoretycznych z zakresu matematyki, automatyki i informatyki [778–782] i w latach 90. zaczęto stosować ją w inżynierii materiałowej do modelowania procesu krystalizacji i rekrystalizacji [783, 784].
Algorytmy wykorzystujące koncepcję automatów komórkowych opisują ewolucję dyskretnego układu w przestrzeni i czasie. Ewolucja ta, zachodzi dla wszystkich komórek składających się na rozpatrywany układ, zgodnie z lokalnymi lub globalnymi regułami wyboru (przejścia), które mogą być określone zarówno deterministyczne jak i probabilistyczne. Wybór stanu każdej z komórek (przejście do nowego stanu albo zachowanie istniejącego), dokonuje się w kolejnych krokach działania algorytmu, które można utożsamiać z upływającym czasem. W najprostszych modelach CA, stan komórki w kolejnym kroku zależy jedynie od aktualnego stanu jej najbliższych sąsiadów (sąsiedztwa) i jest opisywany deterministycznymi regułami wyboru. W przestrzeni dwuwymiarowej, która została zdyskretyzowana siatką kwadratową, reguły wyboru określone są najczęściej na podstawie stanu czterech sąsiadów – sąsiedztwo Moore’a, albo ośmiu – sąsiedztwo von Neumanna [785, 786]. Zmiana stanu komórki w takim układzie może zachodzić, gdy stan założonej liczby sąsiadów jest różny od stanu rozpatrywanej komórki. Oprócz ściśle deterministycznych reguł wyboru, stosowane są również reguły, w których przejście do nowego stanu jest dodatkowo uzależnione od warunku probabilistycznego.

Przykład rekonstrukcji przeprowadzonej na podstawie algorytmu CA [787], przedstawiony został na rysunku 2.13. W pierwszym kroku wygenerowane zostają losowe pozycje i orientacje krystalograficzne dla ,,zarodków krystalizacji” (rys. 2.13a). Następnie, w kolejnych krokach działania algorytmu, dla wszystkich komórek w rozpatrywanej przestrzeni, sprawdzane jest sąsiedztwo Moore’a i podejmowana decyzja o zachowaniu bądź zmianie stanu. Ewentualna zmiana stanu komórki, będąca wynikiem spełnienia warunku wyboru przy założonym sąsiedztwie, zachodzi jednak z prawdopodobieństwem \(P =\)0.5. W przedstawionym przykładzie przyjęto, że zmiana stanu komórki jest możliwa, gdy przynajmniej jedna z komórek w sąsiedztwie będzie w stanie ,,krystalicznym”. Wtedy rozpatrywana komórka może zmienić stan na krystaliczny i odziedziczyć orientację krystalograficzną po sąsiadujących z nią komórkach. W efekcie, po zaledwie kilkudziesięciu krokach działania algorytmu, uzyskiwana jest syntetyczna dwuwymiarowa mikrostruktura polikryształu (rys. 2.13f).
Pomimo zastosowania prostych reguł wyboru, które często nie mają jednoznacznie określonego sensu fizycznego, możliwe jest uzyskanie syntetycznych mikrostruktur, jakościowo, a niekiedy również ilościowo, oddających budowę polikryształów [785, 786]. Ustalenie warunków początkowych i reguł wyboru pozwala zatem na symulację złożonych procesów fizycznych zachodzących w czasie i przestrzeni. Procesami takimi, a w szczególności rozrostem ziaren, można sterować poprzez wprowadzenie bardziej złożonych, fizycznych reguł wyboru [785]. Reguły takie mogą opisywać ruch dyslokacji i kinetykę wzrostu kryształów, mogą również narzucać uprzywilejowane kierunki rozrostu krystalitów. Pozwalają zatem na uzyskanie statystycznie równoważnych rekonstrukcji mikrostruktury, ale przede wszystkim umożliwiają symulacje zjawisk zachodzących w analizowanych polikryształach w miarę upływu czasu [789–795].
Metoda Monte Carlo (MC), podobnie jak koncepcja automatów komórkowych, została opracowana w latach 40. przez Ulama 50 , który wraz z von Neumannem i Metropolisem, sformułował algorytm pozwalający na analizę problemu dotyczącego dyfuzji neutronów w materiale rozszczepialnym [797]. Metoda Monte Carlo z czasem rozwinęła się w całą klasę algorytmów, opierających się na wielokrotnym losowym próbkowaniu. Uśredniona wartość uzyskanych w ten sposób wyników, pozwala na znalezienie przybliżonego rozwiązania dla wielu złożonych problemów, których rozwiązanie metodami analitycznymi jest bardzo czasochłonne albo praktycznie niemożliwe [798, 799]. W latach 80. metodę Monte Carlo zaczęto stosować również w inżynierii materiałowej do symulacji procesu spiekania, kinetyki rozrostu ziaren i rekrystalizacji [800–805].
Aby wykorzystać algorytmy MC do generowania syntetycznej mikrostruktury materiału oraz przeprowadzenia symulacji jej ewolucji w czasie, stosowany jest najczęściej model Pottsa [806] (q-Potts). W modelu tym, analizowana struktura mapowana jest na dyskretną, dwu- lub trójwymiarową siatkę komórek. Komórki takie posiadają charakterystyczne stany \(Q\) (określające np. orientację krystalograficzną), które mogą ulegać zmianie w zależności od stanu układu, a w szczególności ich otoczenia. Sąsiadujące ze sobą komórki o jednakowych stanach \(Q\) tworzą domeny (ziarna). Taka implementacja modelu Pottsa, pozwalająca na przeprowadzenie symulacji metodą Monte Carlo (MC-Potts), jest więc bardzo podobna do koncepcji wykorzystywanej w modelach opartych na CA – szczególnie tych, w których stosowane są probabilistyczne reguły przejścia. Zasadnicza różnica polega jednak na postaci funkcji wyboru, która w przypadku MC-Potts opiera się na redukcji energii swobodnej sieci komórek [789].
Energia pojedynczej komórki (MCU, ang. Monte Carlo Unit) związana ze stanem komórek z nią sąsiadujących i dana jest Hamiltonianem [800, 805]: \[\label{eq:MCUenergy} E_i = J \sum\limits_{j=1}^{n} \left(1 - \delta_{Q_i Q_j}\right)\!,\] przy czym \(J\) jest stałą wyrażającą energię oddziaływania rozpatrywanej MCU z sąsiadującymi z nią komórkami posiadającymi różny od niej stan \(Q\) (energią granic międzyziarnowych). Liczba sąsiadujących komórek \(n\) zależy od przyjętego w modelu wymiaru przestrzeni oraz rodzaju i zasięgu sąsiedztwa. Przykładowo, w przestrzeni 2D dla sąsiedztwa von Neumanna opartego na komórkach stykających się bezpośrednio z rozpatrywaną MCU, \(n = 8\), a w przestrzeni 3D \(n = 26\). Dodatkowo, w powyższym równaniu, \(\delta_{Q_i Q_j}\) to delta Kroneckera.
Prawdopodobieństwo przyjęcia przez komórkę do nowego stanu \(Q'\) można zatem zapisać równaniem warunkowym [800, 805]: \[\label{eq:MC_trans_prob} p\left( \Delta E_i \right) = \begin{cases} 1 & \quad \text{gdy: } \Delta E_i \leqslant 0,\\ \exp \left( - \dfrac{\Delta E_i }{k_{\text{B}}T_{\text{MC}} } \right) & \quad \text{gdy: } \Delta E_i > 0, \end{cases}\] w którym \(\Delta E_i\) jest różnicą energii MCU wynikającą ze zmiany stanu (\(Q \rightarrow Q'\), \(\Delta E_i = E_i' - E_i\)), \(k_{\text{B}}\) stałą Boltzmanna, a \(T_{\text{MC}}\) temperaturą symulacji.
Jeśli więc zmiana stanu komórki wywoła lokalne obniżenie energii (\(E_i' < E_i\)) albo nie spowoduje lokalnego wzrostu energii (\(\Delta E_i = 0\)), to komórka taka przyjmie nowy stan. Natomiast w przypadku wzrostu energii, zmiana stanu jest możliwa z prawdopodobieństwem uzależnionym od czynnika temperaturowego \(\exp \left(- \frac{\Delta E}{k_{\text{B}}T_{\text{MC}} }\right)\). Należy jednak zaznaczyć, że \(T_{\text{MC}}\) jest jedynie parametrem symulacji MC regulującym stopień zaburzenia siatki komórek [805] i nie odpowiada rzeczywistej wartości temperatury procesu, dlatego często czynnik \(J/\left( k_{\text{B}}T_{\text{MC}} \right)\) grupujący stałe, zastępowany jest współczynnikiem temperaturowym \(\alpha\) lub \(\beta\) (\(\alpha = J\beta\)).

Na rysunku 2.14 przedstawione zostały kolejne kroki symulacji rozrostu ziaren przeprowadzonej metodą MC-Potts. Dobierając wartości parametrów symulacji (\(T_{\text{MC}}\), \(\alpha\)), rodzaj i zasięg sąsiedztwa, albo wprowadzając specyficzne funkcje opisujące prawdopodobieństwo zmiany stanu komórek, można uzyskiwać różnorodne modele geometryczne i symulować procesy zachodzące w materiałach polikrystalicznych [807–811]. W ten sposób, z powodzeniem, uzyskiwane są dwu- i trójwymiarowe syntetyczne mikrostruktury jedno- i wielofazowych polikrystalicznych materiałów ceramicznych [800, 812]. Prowadzone są symulacje rozrostu ziaren uwzględniające porowatość i obecność nanometrycznych wtrąceń [812–816] oraz procesu spiekania zarówno w stanie stałym jak i w obecności fazy ciekłej [812, 813, 817, 818].
Wielokrotne próbkowanie rozpatrywanej przestrzeni i ustalanie nowych stanów dla wylosowanych komórek, prowadzi do stopniowego obniżenia energii całego rozpatrywanego układu. Liczba kroków algorytmu (MCS, ang. Monte Carlo Step) niezbędna do uzyskania minimum energii jest uzależniona od całkowitej liczby komórek i możliwych stanów w rozpatrywanym układzie. Szczególnie w przypadku trójwymiarowych rekonstrukcji mikrostruktury, których celem jest uzyskanie reprezentatywnych populacji ziaren, liczba MCS jest bardzo duża, co znacząco wydłuża czas symulacji [811, 819]. Dlatego oprócz wykorzystania zmodyfikowanych algorytmów, bazujących na ograniczonej liczbie stanów, które mogą przyjmować MCU leżące w granicach ziarnowych [805, 819–822], do symulacji MC-Potts wprowadzane są wstępnie zrekonstruowane siatki komórek. Takie uproszczone reprezentacje mikrostruktury, uzyskane najczęściej metodami geometrycznymi, stanowią układ wejściowy, który jest następnie optymalizowany metodą MC-Potts. Tego typu rozwiązanie przyspiesza symulacje i pozwala dodatkowo na wykorzystanie danych doświadczalnych uzyskanych metodami analizy powierzchni (np. EBSD), dotyczących rozkładu orientacji krystalograficznych [678, 823, 824].
W metodach hybrydowych, oprócz informacji o orientacji krystalograficznej do symulacji MC-Potts wprowadzane są również informacje o pozycji i kształcie ziaren, pochodzące z pomiarów przeprowadzonych metodami tomograficznymi. Pozwala to znacząco skrócić czas pomiarów bez istotnego pogorszenia jakości uzyskanych w ten sposób rekonstrukcji mikrostruktury [742, 745, 825].
Sama koncepcja, na której opiera się metoda Monte Carlo, była wykorzystana dużo wcześniej w 1777 roku przez Buffona [796], który opierając się na prawdopodobieństwie geometrycznym, wyznaczył przybliżoną wartości liczby \(\pi\).↩︎
Do trzeciej grupy metod, pozwalających na uzyskanie cyfrowej reprezentacji mikrostruktury, można zaliczyć metody geometryczne. Są one często wykorzystywane na etapie przygotowania modeli w symulacjach zjawisk mechanicznych, pozwalają na uzyskanie uproszczonej reprezentacji mikrostruktury w metodach doświadczalnych, a także stanowią podstawę do symulacji prowadzonych metodami CA i MC. Tak szerokie pole zastosowań metod geometrycznych, wynika ze stosunkowo niewielkiego kosztu obliczeniowego niezbędnego do uzyskania syntetycznej mikrostruktury. Wspólną cechą metod geometrycznych jest idealizacja kształtu elementów mikrostruktury. Powoduje to daleko idące uproszczenie modeli geometrycznych, które może być pożądane w przypadku symulacji mechanicznych. Zmniejszenie rozmiaru danych opisujących syntetyczną mikrostrukturę, poprawia efektywność symulacji i tym samym pozwala na prowadzenie analiz dla rozległych obszarów, zawierających dużą populację elementów mikrostruktury. Jednak w przypadku, gdy rzeczywista mikrostruktura materiału składa się z elementów o zróżnicowanym i skomplikowanym kształcie, zbyt duże uproszczenie geometrii modelu obliczeniowego, może prowadzić do pominięcia w analizie istotnych oddziaływań i uzyskania niedokładnych, albo wręcz błędnych, wyników symulacji. Dlatego decyzja o wyborze metod geometrycznych w celu rekonstrukcji mikrostruktury, czy do tworzenia modeli wirtualnych materiałów, powinna być poprzedzona analizą wpływu wprowadzanych uproszczeń na symulowane zjawiska.
W przypadku materiałów kompozytowych, granularnych czy komórkowych, w których kształt wyróżnionych elementów mikrostruktury – wtrąceń, cząstek czy porów, jest możliwy do przybliżenia prostymi figurami geometrycznymi – elipsoidami, wielościanami, walcami, słupami, płytkami itp., do trójwymiarowej rekonstrukcji wykorzystywane są algorytmy rozmieszczające założony zestaw elementów w przestrzeni modelu geometrycznego [458, 826–831]. Zarówno kształt, rozmiar jak i orientacja wybranych figur, mogą być zmienne i określone regułami stochastycznymi albo założonym rozkładem empirycznym. Efektywność takich algorytmów zależna jest od przyjętego kształtu elementów, warunków brzegowych (np. periodyczności modelu) i optymalizacyjnych (zakazu nakładania się) i spada wraz ze wzrostem udziału objętościowego generowanych elementów [832]. Pomimo ograniczeń wynikających z uproszczeń dotyczących geometrii generowanych figur, jest to jednak szybka i wydajna metoda pozwalająca na uzyskanie modeli służących do symulacji wielu zjawisk mechanicznych oraz cieplnych zachodzących w kompozytach, materiałach granularnych oraz komórkowych [178, 246, 339, 540, 826, 833].
Do odwzorowania mikrostruktury materiałów polikrystalicznych niezbędny jest opis uwzględniający specyfikę poszczególnych krystalitów. Przyjmując, że tego typu materiały wykazują często praktycznie całkowite wypełnienie przestrzeni – ich porowatość nie przekracza kilku procent, wspomniane powyżej algorytmy rekonstrukcyjne stają się nieefektywne. Dodatkowo, generowane w ten sposób modele mikrostruktury, nie są statystycznie równoważne mikrostrukturze rzeczywistych materiałów polikrystalicznych. Dlatego do rekonstrukcji budowy materiałów polikrystalicznych stosowane są metody opierające się na podziale (teselacji) przestrzeni modelu.
Najprostszym rozwiązaniem jest podział wykorzystujący arbitralnie przyjęte, regularne wielokąty, którymi całkowicie wypełniana jest analizowana przestrzeń modelu. W przypadku modeli trójwymiarowych, stosowane są w tym celu najczęściej sześciany [459, 834], dwunastościany [835, 836], czternastościany [459, 837], albo układy mieszane, składające się np. z sześcianów i osiemnastościanów [459]. W ten sposób, przy niewielkim koszcie obliczeniowym, można uzyskać modele geometryczne, które w sposób uproszczony odwzorowują mikrostrukturę polikryształu (zob. rys. 2.1b). Modele te jednak nie oddają zróżnicowania kształtu i rozmiaru krystalitów, który obserwowany jest w rzeczywistych polikryształach. Dlatego, aby uzyskać dokładniejsze odwzorowanie uwzględniające zmienność morfologii, wykorzystywane są inne metody teselacyjne.
Zmienność kształtu i rozmiaru krystalitów w rekonstruowanych bądź syntetycznych mikrostrukturach, można uzyskać dzięki teselacji Voronoı̈a [838]. Metoda ta wykorzystuje do podziału przestrzeni płaskie powierzchnie, a w przypadku 2D – proste, dzielące tę przestrzeń na komórki teselacyjne. Powierzchnie te albo proste są prostopadłe do prostych łączących sąsiadujące ze sobą ,,punkty zarodkowe” i są równo od nich oddalone. W efekcie takiego podziału przestrzeni, wewnątrz komórek teselacyjnych znajdują się wszystkie punkty, których odległość od punktu zarodkowego w danej komórce jest mniejsza niż odległość do dowolnego innego punktu zarodkowego sąsiadującej komórki. Ta intuicyjna i uniwersalna koncepcja, stosowana jest w różnych dziedzinach, w których analizowane są zagadnienia związane z podziałem przestrzeni. Teselacja Voronoı̈a, oprócz problemu związanego z rekonstrukcją mikrostruktury, wykorzystywana jest więc w analizie obrazu [530, 603], krystalografii [839–841], ale również w zagadnieniach z zakresu geografii, kartografii, meteorologii czy klimatologii [842–844], astronomii [845, 846], biologii, ekologii i epidemiologii [847–851], a nawet socjologii, ekonomii, zarządzania czy lingwistyki [852, 853].
Dla dowolnego punku zarodkowego \(S_i\), wybranego w rozpatrywanej przestrzeni \(\Omega\), obszar odpowiadającej mu komórki \(C_i\), można opisać zależnością [237, 840]: \[\label{eq:Voronoi} C_i = \lbrace x \in \Omega: \Vert x - S_i \Vert < \Vert x - S_j \Vert \rbrace,\quad \text{dla } j \neq i,\] w której \(\Vert x - S_i \Vert\) jest odległością (metryką Euklidesową 51 ) miedzy dowolnym punktem \(x\) należącym do analizowanej przestrzeni \(\Omega\) a wybranym punktem zarodkowym \(S_i\), natomiast \(S_j\) jest punktem zarodkowym innej komórki \(C_j\) z tej przestrzeni.
Aby nadać sens fizyczny powyższej zależności i zastosować ją do rekonstrukcji mikrostruktury, liczbę punktów zarodkowych – a w konsekwencji liczbę komórek teselacyjnych odpowiadających krystalitom, ustala się na podstawie rozmiaru rozpatrywanej przestrzeni. Można w tym celu wykorzystać, wyznaczoną na podstawie analizy mikrostruktury, liczbę cząstek przypadającą na jednostkową objętość \(N_V\), albo wyznaczyć liczbę punktów zarodkowych w oparciu o związki geometryczne pomiędzy rozmiarem przestrzeni (objętością w 3D, lub powierzchnią w 2D) a zakładanym, przeciętnym rozmiarem krystalitów. Następnie, dla określonej w ten sposób liczby punktów, ustalane są współrzędne. Mogą one zostać dobrane w stochastycznym procesie Poissona (teselacja Poissona–Voronoı̈a), w którym współrzędne te są niezależnymi zmiennymi losowymi [854–856], co skutkuje przypadkowym ułożeniem krystalitów. Niekiedy, stosowane są również dodatkowe ograniczenia dotyczące minimalnej odległości między punktami zarodkowymi: \(\Vert S_i - S_j \Vert > 2r_{\text{min}}\) (teselacja Harcore–Voronoı̈) [773, 857]. Uzyskane w ten sposób syntetyczne mikrostruktury charakteryzują się bardziej równomiernym pokrojem krystalitów, a parametr \(r_{\text{min}}\) pozwala kontrolować ich minimalny rozmiar (\(V_c > \frac{4}{3} \pi r_{\text{min}}^3\)) [621, 773, 858, 859]. Pozycje punktów zarodkowych mogą być również ustalone na podstawie specyficznych funkcji rozkładu przestrzennego. Pozwala to na odwzorowanie niejednorodności w polikrysztale: gradientu czy lokalnych fluktuacji rozmiaru krystalitów, oraz klasteryzacji struktury [580, 593, 855, 860, 861].
Wykorzystywane do teselacji Voronoı̈a algorytmy umożliwiają także optymalizację kształtu generowanych komórek. Jest ona realizowana poprzez stopniową zmianę pozycji punktów zarodkowych. W kolejnych krokach działania algorytmu (najczęściej stosowany jest tutaj algorytm Lloyda [862]), punkty zarodkowe przesuwane są w nowe pozycje, odpowiadające środkom masy (centroidom) wygenerowanych komórek teselacyjnych. Następnie, dla nowych pozycji, ponownie przeprowadzana jest teselacja. Taka optymalizacja struktury kontynuowana jest do momentu osiągnięcia przez układ zakładanego kryterium zbieżności [863]. Teselacja prowadzona w ten sposób (teselacja Centroidal–Voronoı̈ [864]) pozwala na uzyskanie syntetycznej mikrostruktury, składającej się z jednorodnie rozmieszczonych krystalitów, reprezentowanych przez wielościany o regularnych kształtach i zbliżonej objętości [621, 865].
Oprócz kształtu komórek teselacyjnych, który zbliżony jest do kształtu krystalitów obecnych w wielu materiałach ceramicznych i metalicznych, również parametry topologiczne sieci Voronoı̈a wykazują istotne podobieństwo do parametrów charakterystycznych dla rzeczywistych polikryształów. W przestrzeni trójwymiarowej, statystycznie każda krawędź styka się z trzema komórkami i dwoma wierzchołkami, a każdy wierzchołek, łączy cztery krawędzie, sześć ścian i cztery komórki [854, 866].
Wymienione cechy struktur uzyskiwanych poprzez teselację Voronoı̈a sprawiły, że od ponad 20 lat są one intensywnie wykorzystywane w modelowaniu numerycznym materiałów polikrystalicznych i komórkowych. Jednymi z pierwszych prac, w których struktury te zostały zastosowane do analiz numerycznych 52 , były prace Canova i in. [869] dotyczące modelowania odkształceń w polikrystalicznym kwarcu i materiale składającym się z kwarcu i miki, oraz prace Kumara i in. [866, 870]. Kumar i in. przeprowadzili analizę ilościową struktur Voronoı̈a dla populacji składających się z 358000 komórek teselacyjnych w 3D oraz 5000 komórek w 2D i dokonali ich statystycznego opisu. Prace te potwierdziły przydatność teselacji Voronoı̈a jako metody pozwalającej na uzyskiwanie trójwymiarowych modeli geometrycznych, mogących odwzorowywać rzeczywistą budowę wielu materiałów polikrystalicznych. Modele te, zaczęto więc stosować, do symulacji zjawisk mechanicznych i termomechanicznych, prowadzonych metodą elementów skończonych [453, 869, 871–875]. W przypadku tworzyw ceramicznych, teselacja Voronoı̈a została wykorzystana do rekonstrukcji i modelowania właściwości polikryształów jednofazowych oraz kompozytów ziarnistych [318, 460, 858, 876–881], a modele geometryczne posłużyły również do symulacji zjawiska kruchego pękania [313, 316, 318, 319, 326, 334, 882].
Przykład dwuwymiarowej struktury komórkowej uzyskanej poprzez teselację Voronoı̈a został przedstawiony na rysunku 2.15. Jak można zauważyć, teselacja Poissona–Voronoı̈a (rys. 2.15a) prowadzi niekiedy do generowania komórek, których kształt jest zbyt uproszczony, aby mogły one wystarczająco dobrze opisywać kształt rzeczywistych krystalitów występujących w materiałach ceramicznych. Szczegółowa analiza statystyczna parametrów topologicznych i morfologicznych (liczby ścian, krawędzi, wierzchołków, rozmiaru i kształtu komórek) wskazuje, że struktury takie stanowić mogą jedynie pierwsze przybliżenie budowy rzeczywistych polikryształów [883]. Lepsze dopasowanie struktury można uzyskać stosując teselację Harcore–Voronoı̈ oraz Centroidal–Voronoı̈ (rys. 2.15b), ale optymalizacja opiera się jedynie na zmianach pozycji punktów zarodkowych, co utrudnia odwzorowanie rozkładu rozmiaru i kształtu krystalitów.
\(d_e(x,S_i) = \Vert x - S_i \Vert = \sqrt{\sum\limits_{k=1}^n \left(x_k - S_{i,k}\right)^2}\), gdzie \(n\) to liczb wymiarów przestrzeni.↩︎
Publikacje dotyczące wykorzystania teselacji Voronoı̈a do opisu mikrostruktury materiałów polikrystalicznych, były prezentowane również wcześniej (np. Wray i in. [867] czy Spitzig i in. [868]), jednak ograniczały się one do zagadnień stereologicznych, związanych z analizą obrazu czy rozkładem przestrzennym cząstek.↩︎
Podobnie jak w przypadku teselacji Voronoı̈a – teselacja Laguerre’a polega na podziale przestrzeni na wypukłe komórki o płaskich ścianach. Zaletą teselacji Laguerre’a, jest to, że umożliwia ona odwzorowanie szerszego zakresu struktur polikrystalicznych i komórkowych, poprzez zastosowanie przy podziale przestrzeni geometrii Laguerre’a, w której każdemu punktowi zarodkowemu \(S_i\) przyporządkowany jest współczynnik wagowy \(w_i\) [884, 885]. Współczynnik ten modyfikuje położenie powierzchni ograniczających komórki teselacyjne (w przestrzeni 2D położenie prostych) i tym samym wpływa na rozmiar tych komórek. Rozszerzając wyrażenie \eqref{eq:Voronoi} opisujące teselację Voronoı̈a o współczynniki \(w_i\), można w sposób analogiczny wyrazić teselację Laguerre’a [752, 840]: \[\label{eq:Laguerre} C_i = \lbrace x \in \Omega: \Vert x - S_i \Vert^2 - w_i < \Vert x - S_j \Vert^2 - w_j \rbrace,\quad \text{dla } j \neq i.\] Rozmiar komórki teselacyjnej Laguerre’a \(C_i\) jest więc modyfikowany współczynnikiem wagowym \(w_i\), który może być interpretowany jako parametr określający promień sfery (albo okręgu w 2D), której środek znajduje się w punkcie zalążkowym \(S_i\) (\(r_i = \sqrt{w_i}\)). W szczególnym przypadku, gdy wszystkie promienie \(r_i = 0\), teselacja Laguerre’a wyraża teselację Voronoı̈a, dlatego nazywana jest również uogólnioną teselacją Voronoı̈a. Przykład dwuwymiarowej struktury uzyskanej poprzez teselację Laguerre’a został przedstawiony rysunku 2.15c.
Przypisanie każdemu punktowi zalążkowemu określonej wagi, umożliwia dopasowanie rozkładu rozmiaru komórek w generowanej strukturze do zakładanego, albo empirycznego, rozkładu rozmiaru krystalitów czy komórek w stałych pianach [615, 752, 826, 886–889]. Dodatkowo w trakcie optymalizacji, możliwe jest również modyfikowanie struktury teselacyjnej, tak aby uzyskać statystyczne odwzorowanie podstawowych parametrów morfologicznych [540, 771, 890–892].
Pozycje punktów \(S_i\) oraz ich współczynniki wagowe \(w_i\), mogą zostać dobrane w procesie Poissona, umożliwiając tym samym generowanie struktur stochastycznych, mogą również zostać ustalone na podstawie zależności teoretycznych (np. zakładanych rozkładów statystycznych) czy danych empirycznych. Dlatego teselacja Laguerre’a jest często wykorzystywana do uzyskiwania zarówno syntetycznych mikrostruktur materiałów polikrystalicznych i komórkowych, jak również do rekonstrukcji opartych na danych doświadczalnych, uzyskanych metodami tomograficznymi, przekrojów seryjnych oraz stereologicznymi [621, 744, 752, 775, 776, 893–896]. W przypadku polikrystalicznych tworzyw ceramicznych, teselacja Laguerre’a znalazła zastosowanie do rekonstrukcji i modelowania mikrostruktury oraz właściwości zarówno materiałów jednofazowych [540, 859, 893, 897] jak i kompozytów ziarnistych [318, 771, 898, 899].
Modele geometryczne uzyskiwane metodami teselacyjnymi (zarówno Voronoı̈a jak i Laguerre’a) mogą wykazywać duże zróżnicowanie rozmiaru elementów strukturalnych – krawędzi i ścian komórek (zob. rys. 2.15d). Taka własność sprzyja dopasowaniu kształtu tych elementów do kształtu rzeczywistych ziaren czy komórek w modelowanej mikrostrukturze. Niekiedy jednak, podczas skalowania modelu geometrycznego do wymiarów odpowiadających rozpatrywanej, rzeczywistej przestrzeni, długości najkrótszych krawędzi mogą osiągać wartości, które tracą sens fizyczny. Przykładowo, dla komórek o wymiarach odpowiadających mikrometrycznym ziarnom, długość najkrótszych krawędzi może osiągać wartości mniejsze niż wartości promieni atomowych [883]. Oprócz ewidentnej niezgodności z parametrami fizykochemicznymi, elementy te powodują również problemy numeryczne. W analizach MES, podczas dyskretyzacji modeli geometrycznych mogą pojawiać się błędy wynikające z zaokrągleń spowodowanych przekroczeniem precyzji pozycjonowania węzłów, deformacją kształtu elementów skończonych czy lokalnym nadmiernym zagęszczeniem siatki [858, 900]. Problemy te nasilają się wraz ze wzrostem anizotropii kształtu komórek teselacyjnych i często dotyczą również komórek o najmniejszych wymiarach [863, 883, 901].
Aby ograniczyć błędy wynikające z obecności najmniejszych elementów strukturalnych (nie mających fizycznego uzasadnienia), już na etapie teselacji, w trakcie optymalizacji generowanej struktury, można przeprowadzić regularyzację geometrii. Jednym ze sposobów, jest zaproponowana przez Queya [900] technika, polegająca na usunięcie krawędzi komórki, której długość jest mniejsza od założonego minimum. Usunięta krawędź i związane z nią dwa wierzchołki zastępowane są jednym wierzchołkiem. Tak przeprowadzona regularyzacja geometrii praktycznie nie wpływa na rozmiar komórek teselacyjnych, ale powoduje zniekształcenie ścian komórek i istotnie zmienia parametry topologiczne. Maleje średnia liczba ścian komórek i tym samym liczba najbliższych sąsiadów [900]. Zmiany te mogą prowadzić do lepszego dopasowania parametrów morfologicznych i topologicznych generowanych struktur do zakładanego rozkładu teoretycznego bądź empirycznego.
Opisane w poprzednich podrozdziałach metody, pozwalające na trójwymiarową rekonstrukcję rzeczywistej mikrostruktury oraz na otrzymywanie mikrostruktury syntetycznej, zostały wybrane spośród tych, które są najczęściej stosowane w badaniach dotyczących polikrystalicznych tworzyw ceramicznych. Z uwagi na szybki rozwój inżynierii materiałowej i wynikające z niego duże zapotrzebowanie na szczegółowe i dokładne obrazowanie budowy wewnętrznej materiałów, opracowywane i rozwijane są też inne niewymienione tutaj metody pomiarowe i symulacyjne [14, 621, 902–909]. Złożoność mikrostruktury, którą charakteryzują się materiały polikrystaliczne, powoduje, że ostateczny dobór metody uwarunkowany jest zarówno specyfiką materiału jak i celem prowadzonych badań.
Podczas analizy budowy wewnętrznej tworzyw, niezwykle cenne są wyniki uzyskiwane metodami doświadczalnymi. Tutaj dobór konkretnej metody uzależniony jest od właściwości fizykochemicznych faz i specyfiki mikrostruktury analizowanego tworzywa (zob. p. 2.5.1). Decydującą jednak kwestią jest dostępności aparatury pomiarowej oraz niezbędna rozdzielczość i rozmiar reprezentatywnej próby, które wymagają zwykle przyjęcia kompromisu [616, 654, 660, 664, 714, 732, 741, 744, 755]. Często zakres pomiarów ograniczany jest do wybranych cech mikrostruktury, co pozwala na istotne skrócenie czasu pomiarowego i tym samym na ograniczenie kosztów badań. Dalsza rekonstrukcja, opierająca się na takich danych, prowadzona jest już metodami symulacyjnymi. Takie połączenie metod, nazywane metodami hybrydowymi, pozwala na uzupełnienie brakujących danych pomiarowych na podstawie znanych związków fizycznych i, dzięki temu, odtworzenie rzeczywistej mikrostruktury tworzyw [744, 756, 825].
Alternatywą dla pomiarów realizowanych bezpośrednio w 3D (tomografii i przekrojów seryjnych), mogą być pomiary prowadzone na dwuwymiarowych przekrojach. Uzyskane metodami stereologicznymi dane, opisujące podstawowe parametry budowy materiału, wykorzystywane są (podobnie jak w metodach hybrydowych) do dalszej rekonstrukcji, prowadzonej metodami geometrycznymi lub symulacyjnymi. Z uwagi na dużą dostępność takiego rozwiązania, jest ono szeroko stosowane w przypadku modelowania właściwości tworzyw. Uzyskiwane w ten sposób modele geometryczne, przy wykorzystaniu odpowiednio dobranej, dużej liczby zebranych danych doświadczalnych, są statystycznie równoważne rzeczywistym mikrostrukturom [540, 594, 771, 826].
Jednak metody symulacyjne i geometryczne stosowane są nie tylko jako uzupełnienie metod doświadczalnych. Pozwalają one przede wszystkim na generowanie syntetycznych mikrostruktur na podstawie teoretycznych związków, opracowanych i rozwijanych w ciągu ostatnich kilkudziesięciu lat w obszarze inżynierii materiałowej. Tego rodzaju podejście pozwala na ograniczenie rozmiaru danych gromadzonych i przetwarzanych w metodach doświadczalnych oraz na bezpośrednią analizę fundamentalnych relacji między mikrostrukturą a właściwościami tworzyw. Dobór metody, spośród metod symulacyjnych czy geometrycznych, oparty jest zazwyczaj na kryterium związanym z liczbą i rodzajem parametrów, którymi może zostać opisany proces generowania mikrostruktury [756, 910, 911]. W przypadku metod symulacyjnych, wykorzystywane są związki opisujące kinetykę wzrostu krystalitów oraz ograniczenia geometryczne. Duża liczba parametrów niezbędna do uwzględnienia wszystkich rozpatrywanych zależności może paradoksalnie utrudniać uzyskanie powtarzalnych i wiarygodnych wyników (wirtualnych mikrostruktur). Szczególnie problematyczne są parametry, które nie mają dobrze określonego związku z odpowiednimi parametrami doświadczalnymi, albo są parametrami numerycznymi. Ustalenie ich wartości wymaga uważnej analizy uzyskiwanych rezultatów i ewentualnej korekcji w trakcie kalibracji modelu [601, 789, 799]. Inne kryterium opiera się na oszacowaniu złożoności geometrycznej modelu, która jest niezbędna do odtworzenia istotnych, dla analizowanego zjawiska, cech mikrostruktury [593, 745, 893, 911].
Związek pomiędzy makroskopowymi właściwościami materiałów a ich budową wewnętrzną jest jednym z głównych paradygmatów w inżynierii materiałowej. Globalna odpowiedź niejednorodnych struktur, takich jak polikryształy czy kompozyty, na zewnętrzne obciążenia, ma swoje źródło w oddziaływaniach lokalnych, zachodzących w skali atomowej, cząsteczkowej, na poziomie krystalitów, ziaren, włókien, porów i warstw. Ustalony w tym zakresie konsensus sprawia, że od wielu lat (co najmniej od końca XIX wieku) poszukiwane są fizyczne związki i metody obliczeniowe, pozwalające powiązać te zależności, a tym samym uzyskać dokładny i precyzyjny, makroskopowy opis, uwzględniający lokalne niejednorodności budowy materiału. Zadanie to jest głównym celem badań mikromechaniki – mechaniki ośrodków niejednorodnych.
Złożoność zagadnienia, wynikająca z liczebności oddziałujących ze sobą elementów budowy i wpływających na makroskopowe, efektywne właściwości materiałów, powoduje, że nie jest możliwy pełny opis, opierający się jedynie na fundamentalnych, kwantowo-mechanicznych związkach dotyczących oddziaływań w skali atomowej. Skalowanie takich modeli (pomijając kwestie wymagań odnośnie infrastruktury obliczeniowej) powoduje, że ilość uzyskiwanych informacji szybko przekracza możliwości ich efektywnego przetwarzania i analizowania w celu uzyskania syntetycznego opisu obiektów o wymiarach zapewniających ich statystyczne podobieństwo do realnych struktur (np. polikryształów). Zjawisko ,,nadmiaru danych” występuje jednak nie tylko w przypadku próby uzyskania opisu opartego na analizie oddziaływań w skali atomowej. Podobne problemy pojawiają się również, gdy opis ograniczony jest do znacznie większych elementów budowy – elementów mikrostrukturalnych. Z drugiej strony, podejście polegające na przyjęciu właściwości materiału jedynie na podstawie jego składu, bez uwzględnienia niejednorodności i specyfiki budowy wewnętrznej, powoduje, że tracony jest element predykcyjny modelu, a uzyskiwane szacunki mogą być zgodne z wynikami pomiarów tylko pod warunkiem spełnienia szeregu założeń. W zagadnieniach z zakresu mikromechaniki, powszechnie stosowaną techniką jest zatem homogenizacja (uśrednianie) parametrów opisujących materiał w jednej skali i szukanie konstytutywnych związków pozwalających połączyć je z parametrami wykorzystywanymi do opisu w kolejnej, wyższej skali. Takie stopniowe podejście nazywane jest modelowaniem wieloskalowym [291, 902, 912, 913].
Początki klasycznych modeli mikromechanicznych, opierających się na rozwiązaniach analitycznych, związane są z pracami Voigta [914], uzupełnionymi później przez Reussa [915]. Modele te, opierające się na regule mieszanin, pozwalają na oszacowanie średnich wartości modułów sprężystości, ale stosowane są również do estymowania wartości innych parametrów termomechanicznych dla materiałów wielofazowych. Przyjęcie założeń dotyczących jednorodnego odkształcenia w modelu Voigta, albo naprężenia w modelu Reussa, sprawia, że wartości średnich modułów sprężystości wyznaczone na podstawie tych modeli, znacznie się od siebie różnią. Na podstawie analizy przeprowadzonej przez Hilla [916], przyjmuje się, że mogą one stanowić jedynie górne i dolne oszacowanie wartości efektywnych (\(\langle E \rangle_{\text{V}} \geqslant E^{*}\geqslant \langle E \rangle_{\text{R}}\)).
Ważnym etapem w rozwoju metod stosowanych w mikromechanice była koncepcja Eshelby’ego [229, 230]. Zaproponował on aproksymację właściwości sprężystych niejednorodnego ciała, opartą na modelu pojedynczej, elipsoidalnej inkluzji, otoczonej nieograniczoną osnową, poddawaną jednorodnym obciążeniom zewnętrznym (rys. 3.1a). W przypadku materiałów kompozytowych, szczególnie kompozytów ziarnistych, model ten – nieuwzględniający oddziaływań między sąsiadującymi inkluzjami – prowadził jednak do nierealistycznych wyników, nawet przy niewielkim udziale objętościowym fazy wtrąconej [917, 918]. Pomimo tego, z uwagi na zwięzły analityczny opis przedstawiony przez Eshelby’ego, idea oparta na ekwiwalentnej inkluzji, stała się podstawą dla wielu innych rozwiązań wykorzystujących koncepcję pola średniego (por. p. 1.4.3). Częściowe uwzględnienie oddziaływań pomiędzy wtrąceniami, w rozwijanych w tym nurcie rozwiązaniach, pozwoliło poprawić zgodność uzyskiwanych wartości estymowanych parametrów z wartościami wyznaczanymi doświadczalnie.
Do takich rozwiązań prowadzi zastosowanie metody pola samouzgodnionego 53 (SCS, ang. Self-Consistent Scheme) wprowadzonej przez Hershey’a [919], Krönera [920], Budiansky’ego [921] i Hilla [922, 923], w którym inkluzja otoczona jest ,,efektywnym medium” (rys. 3.1b). Zastąpienie osnowy takim ośrodkiem – o nie znanych a priori właściwościach, które uzgadniane są dopiero w trakcie obliczeń – pozwoliło na uwzględnienie interakcji między niejednorodnościami i rozszerzenie opisu na jednofazowe materiały polikrystaliczne, w których nie można wyróżnić fazy dominującej (osnowy).
W przypadku materiałów kompozytowych oraz wysokoporowatych, zakres stosowalności SCS ograniczony jest jednak do \(\sim\)40 % udziału objętościowego wtrąceń lub porów [918, 924]. Dla takich materiałów aproksymację właściwości efektywnych można uzyskać stosując uogólnioną metodę pola samouzgodnionego (GSCS, ang. Generalized Self-Consistent Scheme) [925, 926]. Wykorzystywany w niej model wprowadza dodatkową warstwę, przylegającą bezpośrednio do wtrąceń, o właściwościach osnowy. Dlatego model ten nazywany jest niekiedy modelem trójfazowym.
Kolejną koncepcją, ważną dla rozwoju metod analitycznych stosowanych w mikromechanice, była, wspomniana już wcześniej (zob. p. 1.4.3), koncepcja przedstawiona przez Moriego i Tanakę [234]. Pierwotnie dotyczyła ona wyznaczenia średnich naprężeń w osnowie kompozytu ziarnistego, w którego wtrąceniach skumulowane są odkształcenia własne. Jednak w połączeniu z koncepcją ekwiwalentnej inkluzji Eshelby’ego, praca ta stała się podstawą do opracowania wielu schematów obliczeniowych dla różnych zjawisk termomechanicznych – przykładowo: przedstawionych już modeli Taya i in. [415], Hsueha i Bechera [419, 420] oraz innych, szczegółowo omówionych przez Mura [929]. Ostatecznie, Benveniste [930] przeformułował i dokonał ponownej interpretacji równań Moriego–Tanaki. Pozwoliło to na bezpośrednie zdefiniowanie właściwości efektywnych na podstawie uzyskanych równań oraz opracowanie procedury wyznaczenia właściwości efektywnych dla kompozytów. Wykorzystany, w podejściu zaproponowanym przez Benveniste, tensor koncentracji odkształceń (oraz naprężeń), w sposób jawny zależy od udziału objętościowego składnika i może zostać ustalony na podstawie interpolacji pomiędzy odpowiednim tensorem dla ,,rozcieńczonego” medium – gdy zawartość składnika \(f_i \rightarrow 0\) a tensorem dla \(f_i = 1\) [291, 918, 931]. Koncepcja Moriego–Tanaki jest najczęściej stosowana do aproksymacji właściwości termomechanicznych kompozytów, w których wtrącenia mają kształt zbliżony do sferycznego albo elipsoidalnego (rys. 3.1c). Jednak w przypadku modelu opierającego się na elipsoidalnych wtrąceniach, ich udział objętościowy nie powinien jednak przekraczać 20 % [218, 932].
Oprócz wymienionych metod analitycznych stosowanych w mikromechanice do estymowania parametrów termomechanicznych ośrodków niejednorodnych, wykorzystywane są również inne schematy i modele obliczeniowe. Należy wymienić tutaj metodę różnicową opracowaną przez Hashina [933], która jest stosowana w przypadku materiałów porowatych, jak również metodę podwójnej inkluzji zaproponowaną przez Horiego i Nemat-Nassera [934] dla materiałów dwufazowych.
Inna koncepcja, stosowana często do szacowania właściwości efektywnych ośrodków niejednorodnych, opiera się na podejściu niebezpośrednim, polegającym na ujmowaniu poszukiwanych wartości estymowanych parametrów w ,,realizowalnych” granicach [218, 935, 936]. Granice takie wyznaczają zakres możliwych do uzyskania parametrów efektywnych, przy odpowiednio dobranej mikrostrukturze materiału [937–939]. Innymi słowy, wartości parametrów efektywnych wykraczające poza wyznaczony zakres łamią fizyczne ograniczenia i nie mogą opisywać rzeczywistych materiałów.
Na takiej koncepcji oparte są wymienione już granice pierwszego rzędu sformułowane przez Hilla [916], który wykorzystał do ich określenia średnią arytmetyczną Voigta i harmoniczną Reussa. Zakres tych granic, biorących pod uwagę jedynie udział objętościowy składników, jest jednak bardzo szeroki. Na precyzyjniejsze oszacowanie właściwości efektywnych makroskopowo (statystycznie) izotropowych materiałów, pozwalają granice drugiego rzędu wyznaczone przez Hashina i Shtrikmana [232, 940, 941]. Przyjmuje się, że granice te są najwęższym ograniczeniem, które można ustalić bez szczegółowego opisu mikrostruktury materiału: kształtu i rozkładu rozmiarów krystalitów [942–944]. W oparciu o dodatkowe informacje o budowie wewnętrznej materiału, możliwe jest dalsze zawężanie zakresu realizowalnych wartości parametrów poprzez ustalenie granic trzeciego rzędu. W przypadku losowego medium, w ogólnej postaci, zostały one pierwotnie sformułowane przez Berana [945]. Milton i Phan-Thien [946] uprościli formalizm Berana i wykorzystując rachunek wariacyjny oraz transformację Fouriera, wyznaczyli granice dla kompozytu dwufazowego. W przedstawionym przez nich rozwiązaniu, do opisu ilościowego mikrostruktury, została zastosowana funkcja korelacji trójpunktowej [218, 931]. Jednak z uwagi na trudności w uzyskaniu odpowiednich parametrów mikrostruktury niezbędnych do wyznaczenia tego typu granic, w praktyce, nadal wykorzystywane są najczęściej granice Hashina i Shtrikmana.
Warto również zaznaczyć, że wymienione, klasyczne modele analityczne były konstruowane ze szczególnym uwzględnieniem opisu parametrów sprężystych \((\mathcal{K}\), \(\mathcal{G}\)), jednak z uwagi na uniwersalne koncepcje stojące za tymi rozwiązaniami, zostały rozszerzone i wykorzystane również do analizy wielu innych zjawisk termomechanicznych. Zwięzła forma równań i duża efektywność obliczeniowa, sprawia, że metody te są ciągle rozwijane i szeroko stosowane w mikromechanice ośrodków niejednorodnych [20, 93, 599, 947–950]. Pozwalają one na sukcesywną homogenizację w kilku kolejnych skalach dla mikrostruktur o złożonej strukturze hierarchicznej. Z powodzeniem zastosowano je w odniesieniu do polikryształów [938, 944, 951, 952], materiałów porowatych [953–955], kompozytów ziarnistych w różnych skalach: od nanokompozytów po beton [956–959], kompozytów włóknistych [960–963], kompozytów o fazach ciągłych [964] czy struktur kostnych [965] i powierzchni granic międzyziarnowych [948, 966, 967]. Są one również wykorzystywane podczas projektowania i optymalizacji właściwości oraz metod wytwarzania materiałów [968, 969]. Parametry uzyskane dzięki rozwiązaniom analitycznym, charakteryzujące wyidealizowane tworzywa, pomagają również w interpretacji wyników doświadczalnych, stanowiąc estymatory wartości oczekiwanych [970–972]. Metody analityczne są także stosowane na etapie weryfikacji modeli i walidacji wyników symulacji dla metod przybliżonych [177, 178, 268, 338, 459, 594, 833, 872, 879, 880, 901, 939, 950, 962, 973, 974].
Niezależnie jednak od zastosowanego podejścia, uszczegółowienie opisu analitycznego w zakresie kształtu, rozmiaru, orientacji i rozmieszczenia niejednorodności, a w szczególności zróżnicowanie tych cech w modelu, sprawia, że staje się on coraz bardziej skomplikowany. Dodatkowo uwzględnienie nieliniowej odpowiedzi materiału na złożone zewnętrzne obciążenia, prowadzi do równań, których analityczne rozwiązanie jest trudne, a zwykle wręcz niemożliwe. Dlatego w wielu przypadkach, do rozwiązania tak postawionych problemów obliczeniowych, stosowane są metody numeryczne (metoda różnic skończonych czy całkowanie numeryczne) [933, 934, 938, 941, 944, 948, 951, 952, 955, 959, 975, 975–981]. Jednak pełny opis zachowania materiału, uwzględniający złożoność mikrostruktury, która obserwowana i rekonstruowana jest z coraz większą dokładnością (zob. p. 2.5), nie jest możliwy w oparciu o rozwiązania analityczne należące do metod pola średniego (MFT). Dlatego w mikromechanice równolegle rozwijane i wykorzystywane są metody numeryczne, opierające się na dyskretyzacji fizycznej modelu geometrycznego – wirtualnej mikrostruktury.
Metoda, czy schemat obliczeniowy, pola samouzgodnionego w literaturze polskiej określana jest również mianem metody samozgodnej.↩︎
W przeciwieństwie do analitycznych metod homogenizacji opartych na przybliżeniu pola średniego, homogenizacja numeryczna (ang. computational homogenization) może uwzględniać złożone zachowania nieliniowe: geometryczne i materiałowe. Ponadto, ustalane w trakcie obliczeń rozkłady pól naprężeń i odkształceń, umożliwiają analizę inicjacji i rozwoju szczelin. Jest to kluczowy aspekt w przypadku materiałów kruchych, pozwalający na lokalizację niejednorodności mogących przyczyniać się do pękania. Wyniki symulacji, prowadzonych na modelach szczegółowo opisujących budowę wewnętrzną materiału, ułatwiają również bezpośrednie badanie wpływu kształtu, rozmiaru, orientacji krystalitów, wzajemnego ułożenia granic międzyziarnowych, rozmieszczenia wtrąceń, włókien i innych elementów mikrostruktury, zarówno na lokalną jaki i globalną odpowiedź materiału na złożone obciążenia. Stochastyczny charakter tych zależności jest trudny do uwzględnienia w opisie analitycznym, a wykorzystanie w symulacjach wirtualnych mikrostruktur pozwala na ilościowe ujęcie obserwowanych zjawisk [237, 784, 982, 983].
W mikromechanice obliczeniowej, stanowiącej jedną z gałęzi obliczeniowej inżynierii materiałowej, stosowanych jest szereg metod numerycznych (przybliżonych) wykorzystujących wirtualne mikrostruktury, służących do modelowania różnorodnych zagadnień mechanicznych cieplnych czy elektrycznych [913, 984–986]. Najczęściej stosowana jest metoda elementów skończonych (MES, FEM) [25, 200, 268, 291, 374, 459, 771, 784, 987–989] i metody pokrewne: rozszerzona metoda elementów skończonych (XFEM, ang. Extended Finite Element Method) [786, 986–988, 990], metoda elementów brzegowych (BEM, ang. Boundary Element Method) [299, 858, 986, 991–995], czy połączona metoda plastyczności kryształów z MES (CPFEM, ang. Crystal Plasticity Finite Element Method) [988, 989, 996, 997]. Stosowane są również metody różnic skończonych (FDM, ang. Finite Difference Method) [784, 986, 998], objętości skończonych (FVM, ang. Finite Volume Method) [999, 1000] oraz metody bezsiatkowe (ang. Mesh-Free Methods) [402, 1001, 1002]. Szereg wykorzystywanych w mikromechanice technik obliczeniowych opiera się także na wcześniej już wspomnianej metodzie Monte Carlo (MC) [784, 786, 799, 913, 986, 1003, 1004] i koncepcji automatów komórkowych (CA) [786, 791, 794, 913, 1004, 1005] oraz metodach dynamiki molekularnej (MD) [278, 285, 292, 299, 784, 986, 1006] i transformacji Fouriera [1007–1009].
W metodach przybliżonych, opierających się na modelu geometrycznym reprezentującym niejednorodności budowy wewnętrznej materiału, istotne stają się wymiary rozpatrywanej przestrzeni (zarówno geometryczne jak i czasowe). Wynika to z jednej strony z ograniczeń technicznych, dotyczących dostępnej mocy obliczeniowej oraz możliwości przetwarzania i analizowania uzyskiwanych danych (ograniczenie, co do maksymalnych wymiarów modelu), a z drugiej – ze specyfiki samych metod. Wykorzystywane związki konstytutywne i przyjmowane założenia, mogą nie pozwalać na opis zjawisk na najbardziej fundamentalnym poziomie (np. zastosowania przybliżenia kontinuum). Dlatego powszechnie stosowany jest podział metod odnoszący się do skal modelu.
Z uwagi na zróżnicowanie budowy wewnętrznej materiałów nie istnieje ujednolicona klasyfikacja pozwalająca na określenie w sposób ścisły granic między poziomami struktury. Dla wielu materiałów, w oparciu o wymiary przestrzenne, można jednak wydzielić trzy zasadnicze skale budowy (zob. rys. 3.2). Pierwsza z nich to makroskala, która odpowiada obszarowi typowych zainteresowań inżynierskich: projektowaniu, badaniu i kształtowaniu materiałów litych. Skala ta obejmuje wymiary przestrzenne zwykle przekraczające milimetry, a właściwości materiału w tej skali są traktowane jako jednorodne. Wykorzystywane tutaj metody obliczeniowe opierają się na mechanice ośrodków ciągłych (MES/FEM) albo na mechanice płynów (obliczeniowa mechanika płynów, ang. Computational Fluid Dynamics, CFD).
Drugi poziom stanowi mikroskala, w której obecne są niejednorodności budowy wewnętrznej materiałów. Wymiary tych niejednorodności, tradycyjnie mierzone były w mikrometrach. Dzisiaj, w wyniku rozwoju metod badawczych i technologii materiałowej, zakres mikroskali jest znacząco poszerzony i sięga nanometrów. Jest to skala, na której koncentruje się uwaga inżynierii materiałowej, ale także w której rozwijane są techniki wytwarzania podzespołów i części (np. przemysł elektroniczny). Stosowane tutaj metody obliczeniowe to, wymienione w poprzednim punkcie, metody mikromechaniczne. Budowa materiału na tym poziomie jest nazywana mikrostrukturą i decyduje o wielu makroskopowych właściwościach tworzyw (zob. p. 1.3).
Granica między makro- a mikroskalą nie jest ostra. Niekiedy pomiędzy nimi wyróżnia się dodatkowo mezoskalę. Jest to wygodne podejście w przypadku kompozytów włóknistych i laminatów, w których faza umacniająca (zbrojenie) albo warstwy, tworzą wyraźnie odrębną, niejednorodną strukturę wyższego rzędu, która jednak posiada również własną, specyficzną mikrostrukturę. Z drugiej strony, kres mikroskali wyznaczają układy złożone z setek atomów, w których efekty kwantowe zaczynają odgrywać istotną rolę. Obiekty takie nie mogą być już postrzegane jako ,,kontinuum”, a wyraźna ziarnistość nie pozwala na uśrednianie właściwości materiałowych.
Skala atomowa, stanowi więc trzeci poziom struktury. Tradycyjnie poziom ten był przestrzenią badań podstawowych z zakresu chemii i fizyki, ale aktualnie, również tutaj prowadzone są intensywne prace w dziedzinie inżynierii materiałowej. Stosowane w tej skali metody obliczeniowe muszą uwzględniać zarówno kwantowo-mechaniczną (probabilistyczną) naturę oddziaływań, jak i pozwalać na uzyskanie pożądanej precyzji przewidywań. W obliczeniach ab initio do opisu zjawisk kwantowych wykorzystywana jest teoria funkcjonału gęstości (DFT, ang. Density Functional Theory) [45, 46, 48, 1010–1017], kwantowa metoda Monte Carlo (QMC, ang. Quantum Monte Carlo), oraz metody opierające się na potencjale międzyatomowym [1010, 1014]. W układach wieloatomowych, stosowane są również metody oparte na dynamice molekularnej (MD, ang. Molecular Dynamics) [297, 299, 314, 1018–1021], kinetycznych i statystycznych symulacjach metodą Monte Carlo (KMC, ang. Kinetic Monte Carlo, SMC, ang. Statistical Monte Carlo) oraz na modelu Isinga [1022–1025].
Przedstawiony, umowny podział struktury oraz stosowane w wymienionych skalach specyficzne metody obliczeniowe, ilustrują złożoność zagadnień, które muszą zostać uwzględnione przy próbie całościowego opisu: modelowania i symulacji zachowania materiału pod wpływem różnorodnych obciążeń. Takie wieloskalowe ujęcie (ang. multiscale modeling), które w obliczeniowej inżynierii materiałowej stanowi jeden z nurtów badawczych, wymaga połączenia skal (ang. scale-bridging) [917, 1026, 1027]. Można tu wyróżnić dwa zasadnicze podejścia [786, 1026, 1028]. Pierwsze z nich – współbieżne, opiera się na identyfikacji fenomenologicznych związków (równań konstytutywnych) wykorzystujących niewielki zestaw kluczowych parametrów, pozwalających na opis makroskopowego zachowania materiału. Stosowane w tym podejściu metody starają się odwzorować zachowanie materiału w kliku skalach jednocześnie [295, 786, 1029–1034]. Jednak z uwagi na duży koszt obliczeniowy takich rozwiązań, analizy dla rożnych skal zwykle realizowane są równolegle [1031, 1035, 1036]. Dodatkowo, w rozwiązaniach praktycznych, ukierunkowanych na zastosowania inżynierskie, ograniczeniu podlega liczba rozpatrywanych skal do sprzężenia występującego między mikro- a makroskalą [786, 1034, 1035, 1037, 1038].
Inny sposób połączenia skal realizowany jest poprzez podejście sekwencyjne [786, 1026, 1028, 1039]. Polega ono na prowadzeniu symulacji wstępnych, dla skali niższej – bardziej szczegółowej, których wyniki pozwalają na wyznaczenie parametrów niezbędnych do skonstruowania opisu w skali wyższej – ogólniejszej. Najczęściej, w dalszych symulacjach, model szczegółowy nie jest już wykorzystywany i obliczenia wykonywane są jedynie w oparciu o model ogólny [281, 294, 296, 299, 912, 1040–1042]. Takie podejście pozwala na uniezależnienie modelu od źródeł danych wejściowych. Niezbędne parametry mogą zostać uzyskane zarówno w symulacjach wstępnych (prowadzonych na modelu szczegółowym), jak również mogą być uzupełnione danymi zaczerpniętymi z baz materiałowych, w których agregowane i publikowane są wyniki symulacji prowadzonych różnymi metodami obliczeniowymi (tab. [3.1]). Bazy takie, zawierające także dane doświadczalne, zaczynają mieć coraz większe znaczenie w rozwoju obliczeniowej inżynierii materiałowej, pozwalając na swobodną wymianę informacji między ośrodkami badawczymi [1043, 1044]. Gromadzenie i udostępnianie precyzyjnych i zweryfikowanych informacji o materiale, w formie umożliwiającej powtórne ich wykorzystanie 54, jest jednym z założeń zintegrowanego podejścia w obliczeniowej inżynierii materiałowej (ICME, ang. Integrated Computational Materials Engineering, zob. p. 3.5.3).
Niezależnie jednak od przyjętego podejścia do konstruowania modeli mogących całościowo opisać złożone zachowanie materiału, mikrostruktura jest tym poziomem budowy, który przenosi fundamentalne oddziaływania występujące na poziomie atomowym do skali makroskopowej. Lokalizacja niejednorodności, mających pierwszorzędne znaczenie przy rozpatrywaniu inicjacji procesów fizykochemicznych zachodzących w różnych skalach czasowych (pękanie, pełzanie, korozja chemiczna, degradacja termiczna), oraz homogenizacja, pozwalająca na analizę globalnej odpowiedzi materiału na zewnętrzne obciążenia, wymaga określenia rozmiaru przestrzeni, pozwalającego na reprezentatywny opis rozpatrywanych zjawisk. Jest to kluczowe zagadnienie, szczególnie w przypadku podejścia sekwencyjnego.
Wyznaczenie rozmiaru i ,,rozdzielczości” niejednorodnego obszaru, który mysi zostać rozpatrzony w trakcie obliczeń, opiera się na koncepcji rozdzielenia skal [1045]. Skale można wyrazić przy pomocy charakterystycznych dla nich wymiarów liniowych. Dla makroskali, wymiarem takim jest rozmiar ciała – makroskopowej próbki materiału, \(L_{\text{makro}}\), z której wybrany zostaje reprezentatywny obszar mikro- albo mezoskali o wymiarze \(L\), zawierający inkluzje (np. ziarna wtrąceń czy krystality), charakteryzowane przez ich średni rozmiar \(D\) (rys. 3.3). Pomiędzy tymi wymiarami występuje zależność [1045]: \[\label{eq:sep-scale} \left. \begin{aligned} D &< \\ D &\ll \end{aligned} \right\} L \ll L_{\text{makro}},\] w której po lewej stronie dopuszczalne są dwie możliwości: nierówność \(D<L\) może być wystarczająca dla mikrostruktur ze słabym zaburzeniem geometrycznym i słabym niedopasowaniem właściwości, natomiast dla pozostałych materiałów obowiązuje silniejsza zależność miedzy skalami (\(D \ll L\)).
Dwa skrajne wymiary liniowe (\(L_{\text{makro}}\) i \(D\)), określające makroskopowy rozmiar próbki i średni rozmiar niejednorodności, co do zasady, mogą zostać przyjęte a priori – na podstawie pomiarów doświadczalnych albo założeń projektowych. Natomiast liniowy wymiar \(L\), wyznaczający rozmiar reprezentatywnego elementu objętościowego (RVE, ang. Representative Volume Element), który jest ograniczony tylko nierównością \eqref{eq:sep-scale}, silnie zależy od rodzaju mikrostruktury i właściwości fizycznych materiału. Jedynie w szczególnym przypadku, dla mikrostruktury periodycznej, wymiary RVE mogą odpowiadać wymiarom komórki elementarnej w takim układzie. Najczęściej jednak, chociażby w przypadku materiałów polikrystalicznych, kompozytów ziarnistych – czy bardziej ogólnie, materiałów nieposiadających uporządkowanej mikrostruktury, wymiary RVE nie mogą zostać już tak prosto zdefiniowane.
Jednym z formatów, który staje się standardem stosowanym do przechowywania i organizowania dużych ilości danych materiałowych, jest hierarchiczny format danych (HDF).↩︎
Możliwości wydzielenia z niejednorodnego ośrodka pewnej objętości, dla której wyznaczone wartości parametrów fizycznych będą odpowiadać wartościom makroskopowym, jest jednym z głównych założeń mikromechaniki. Taki reprezentatywny element objętościowy, powinien być więc dostatecznie duży, aby posiadać wszystkie cechy charakterystyczne dla całego materiału. W przypadku polikrystalicznych tworzyw ceramicznych, powinien on więc zawierać dużą liczbę krystalitów, porów, mikropęknięć, inkluzji, ziaren, włókien, itp. niejednorodności, tak aby zapewnić pełną reprezentację ich zróżnicowania morfologicznego, orientacji przestrzennej oraz wzajemnego rozmieszczenia i udziału objętościowego wszystkich składników. Z drugiej jednak strony, RVE powinien być na tyle mały w porównaniu do makroskopowej próbki, aby spełniał podany już wcześniej warunek rozdzielenia skal \eqref{eq:sep-scale}, co w praktyce oznacza możliwość przeprowadzenia efektywnych obliczeń mikromechanicznych dla rozpatrywanego ośrodka niejednorodnego.
Koncepcja reprezentatywnego elementu objętościowego pojawiła się już w rozwiązaniach analitycznych dotyczących homogenizacji. Ograniczenie nieskończonego medium, na którym opierała się koncepcja Eshelby’ego, wprowadził Hill [1046]. Postulował on, że reprezentatywny element objętościowy, dla którego uśrednianie właściwości sprężystych pozwoli na uzyskanie właściwości efektywnych, musi być: ,,(a) strukturalnie, całkowicie typowy dla całej niejednorodnej struktury i (b) zawierać wystarczającą liczbę wtrąceń, aby ogólne (średnie) moduły sprężystości były niezależne od wartości powierzchniowych sił i przemieszczeń, tak długo jak wartości te są <<makroskopowo jednorodne>>” [1046]. W przypadku rozwiązań analitycznych, wywodzących się z koncepcji Eshelby’ego, tak ogólne sformułowanie granic rozpatrywanej przestrzeni, było zaletą, jednak przechodząc do rozwiązań opartych na metodach numerycznych, wykorzystujących modele mikrostruktury, precyzyjne określenie rozmiaru RVE ma krytyczne znaczenie i w tym sensie, definicja podana przez Hilla jest niewystarczająca.
Jedne z pierwszych, precyzyjnych oszacowań rozmiaru RVE, nakierowanych na rozwiązania numeryczne, zawierały prace Saba [1047], Drugana i Willisa [1048] oraz Guseva [1003]. Wykorzystywały one podejście statystyczne i opierały się na analizie fluktuacji średnich wartości składowych modułów sprężystości. Uzyskane przez Drugana i Willisa oraz Guseva wyniki dla kompozytów zawierających izolowane, losowo rozmieszczone, kuliste wtrącenia, wskazywały, że rozmiar RVE jest ,,nieoczekiwanie” mały przy dopuszczalnym, kilkuprocentowym błędzie wyznaczenia wartości efektywnych 55. Na tej podstawie Drugan i Willis, podali w swojej pracy pragmatyczną definicję RVE, przyjmując, że jest to ,,najmniejszy element objętości materiału kompozytowego, dla którego <<ogólny moduł>> będący jego makroskopową reprezentacją, jest wystarczająco dokładnym modelem, by reprezentować średnią odpowiedź konstytutywną” [1048].
Opierając się na przytoczonych definicjach, można przyjąć, że uśrednione (ogólne) wartości parametrów fizycznych, opisujących makroskopową odpowiedź materiału na zewnętrzne bodźce (obciążenia), wyznaczone dla objętości równej bądź większej od RVE, będą właściwościami efektywnymi. W przypadku nie spełnienia tego warunku, uzyskiwane parametry nazywane są pozornymi. Szczegółową analizę zależności pomiędzy właściwościami efektywnymi a pozornymi, przeprowadził Huet [1049]. Na przykładzie modułów sprężystości, wyrażonych tensorami sztywności \(\mathbf{C}\) i podatności sprężystej \(\mathbf{S}\), Huet wyprowadził relacje, które można zapisać równaniami [1049]: \[\label{eq:HuetC} \langle \mathbf{C}^{-1} \rangle^{-1} \leqslant \mathbf{C}^{\text{app}}_{\sigma\text{f}} \leqslant \mathbf{C}^{\text{app}}_{\sigma\text{c}} \leqslant \mathbf{C}^{*} \leqslant \mathbf{C}^{\text{app}}_{\varepsilon\text{c}} \leqslant \mathbf{C}^{\text{app}}_{\varepsilon\text{f}} \leqslant \langle \mathbf{C} \rangle,\] \[\label{eq:HuetS} \langle \mathbf{S}^{-1} \rangle^{-1} \leqslant \mathbf{S}^{\text{app}}_{\varepsilon\text{f}} \leqslant \mathbf{S}^{\text{app}}_{\varepsilon\text{c}} \leqslant \mathbf{S}^{*} \leqslant \mathbf{S}^{\text{app}}_{\sigma\text{c}} \leqslant \mathbf{S}^{\text{app}}_{\sigma\text{f}} \leqslant \langle \mathbf{S} \rangle,\] w których \(\mathbf{C}^{*}\) i \(\mathbf{S}^{*}\) oznaczają efektywne moduły sprężystości; granice dolne wyznaczają średnie harmoniczne (Reussa) \(\langle \mathbf{C}^{-1} \rangle^{-1}\) i \(\langle \mathbf{S}^{-1} \rangle^{-1}\) oraz górne, średnie arytmetyczne (Voigta) \(\langle \mathbf{C} \rangle\) i \(\langle \mathbf{S} \rangle\); tensory wyznaczone dla objętości mniejszych od RVE, opisujące parametry pozorne, oznaczone są indeksem górnym \(^{\text{app}}\) (ang. apparent). Przedstawione zależności zostały wyprowadzone przez Hueta dla kinematycznych i statycznych warunków brzegowych, które z kolei oznaczone są odpowiednio indeksami dolnymi \(_\varepsilon\) i \(_\sigma\). Dodatkowo, w nierówności uwzględnione zostały parametry pozorne wyznaczone dla mniejszych i większych elementów objętościowych, odpowiednio oznaczonych indeksami \(_\text{f}\) i \(_\text{c}\).
Wyniki pracy Hueta [1049], potwierdzają wspomniane już wcześniej rozważania Hilla [916], który wyznaczył granice modułów sprężystości dla ośrodków niejednorodnych, opierając się na średnich Reussa i Voigta. Huet stwierdził ponadto, że granice te stanowią zawsze dolne i górne oszacowanie, w którym muszą zawierać się wartości pozorne, niezależnie od rozmiaru analizowanej przestrzeni i przyjętych warunków brzegowych. Analizując zależność dla tensora sztywności \(\mathbf{C}\) \eqref{eq:HuetC}, można zauważyć, że dolne oszacowania wartości pozornych wykorzystują statyczne warunki brzegowe i zbliżają się do wartości efektywnej wraz ze wzrostem rozważanej objętości \(\mathbf{C}^{\text{app}}_{\sigma\text{f}} \leqslant \mathbf{C}^{\text{app}}_{\sigma\text{c}} \leqslant \mathbf{C}^{*}\). Z kolei stosując kinematyczne warunki brzegowe, uzyskiwane są górne oszacowania wartości pozornych \(\mathbf{C}^{*} \leqslant \mathbf{C}^{\text{app}}_{\varepsilon\text{c}} \leqslant \mathbf{C}^{\text{app}}_{\varepsilon\text{f}}\). Tutaj również zwiększanie objętości prowadzi do zbliżania się wartości pozornych do wartości efektywnej. Analogiczną analizę można przeprowadzić także na podstawie równania \eqref{eq:HuetS}, dla tensora podatności sprężystej \(\mathbf{S}\) – z tym że, dolne oszacowanie osiągane jest tutaj przy zastosowaniu kinematycznych warunków brzegowych, a górne – warunków statycznych.
Na podstawie wyprowadzonych relacji \eqref{eq:HuetC} \eqref{eq:HuetS}, pomiędzy rozmiarem rozpatrywanej przestrzeni a uzyskiwanymi modułami sprężystości, Huet zauważył, że jeśli objętość osiągnie rozmiar RVE, to wyznaczone wartości pozorne będą wartościami efektywnymi. W praktyce oznacza to, że wraz ze wzrostem rozmiaru analizowanej przestrzeni, zawężają się granice, między którymi znajduje się poszukiwana wartość efektywna. Implikuje to również stwierdzenie, że jeśli dla próbek niejednorodnego materiału, o objętości równej bądź większej od RVE, badane będą makroskopowe właściwości, to uzyskane w ten sposób wartości mierzonych parametrów nie powinny wykazywać rozrzutu [1050].
Zbieżność wartości pozornych do wartości efektywnej wraz ze zwiększaniem rozmiaru analizowanej przestrzeni mikrostruktury – obliczeniowego okna mikrostrukturalnego, była wielokrotnie analizowana przy zastosowaniu różnych warunków brzegowych [590, 1050–1057]. Prowadzone badania obejmowały szeroki zakres niejednorodności, dotyczący kształtu, orientacji oraz rozmieszczenia cząstek i potwierdziły obserwacje Hueta, zarówno co do wpływu rozmiaru przestrzeni jak i zastosowanych warunków brzegowych na rozpiętość granic wartości pozornych (rys. 3.4). W tym kontekście warto również zwrócić uwagę na prace, w których analizowano periodyczne warunki brzegowe (PBC, ang. Periodic Boundary Conditions) [771, 1056–1062]. Wyniki tych prac wskazują, że zastosowanie PBC przy wybranym rozmiarze analizowanej przestrzeni, pozwala na lepsze oszacowanie właściwości średnich niż w przypadku zastosowania warunków kinematycznych (przemieszczeniowych) i statycznych (naprężeniowych) (zob. rys. 3.4). Wniosek ten pozostaje prawdziwy, nawet gdy mikrostruktura nie jest globalnie periodyczna. W materiałach posiadających polikrystaliczną budowę nie jest obserwowane uporządkowanie dalekiego zasięgu w odniesieniu do krystalitów. Jednak w modelach geometrycznych wykorzystywanych w symulacjach numerycznych, przyjmowana jest lokalna periodyczność, odpowiadająca rozmiarom całego modelu (zewnętrzne granice są względem siebie periodyczne).
Rozmiar reprezentatywnego elementu objętościowego jest jednak uwarunkowany nie tylko czynnikami mikrostrukturalnymi. Zależy on również od samych właściwości materiałowych poszczególnych składników: symetrii krystalitów i wynikającej z niej anizotropii [1063]. W kontekście obliczeniowym, rozmiar RVE może zatem być różny dla danego materiału niejednorodnego w zależności od analizowanej właściwości. Przykładowo, rozpatrując przewodnictwo cieplne jednofazowego polikryształu, którego krystality posiadają strukturę krystaliczną należącą do układu regularnego, trzy współczynniki tensora przewodnictwa cieplnego (tensor drugiego rzędu) będą sobie równe [49]. Krystality takie, będą więc wykazywać izotropię dla tej właściwości, a więc rozmiar RVE będzie nieskończenie mały. Rozpatrując jednak właściwości sprężyste, odpowiednie tensory (\(\mathbf{C}\) albo \(\mathbf{S}\)) dla tego samego polikryształu, będą posiadać trzy różne współczynniki (np. \(C_{11}\), \(C_{12}\), \(C_{44}\)). Zatem krystality będą anizotropowe, a więc rozmiar RVE musi być już na tyle duży, aby obejmować swoimi rozmiarami odpowiednio dużą ich populację [1063]. Szczegółową analizę rozmiaru RVE dla różnych metalicznych materiałów polikrystalicznych, których krystality należą do układu regularnego, przedstawili Ren i Zheng [1063]. Nawet w tym najprostszym układzie krystalograficznym, różnice w rozmiarze RVE, wynikające z anizotropii krystalitów, były znaczące.
Ilościowo problem ten został opisany przez Nygårdsa [1064]. Posłużył się on dwu- oraz trójwymiarowymi modelami mikrostruktury, zawierającymi różną liczbę ziaren, i stosując periodyczne warunki brzegowe, analizował rozrzut naprężeń zredukowanych, wywołanych jedno- lub dwuosiowym obciążeniem. Na podstawie przeprowadzonych analiz, znalazł liniową zależność pomiędzy anizotropią, wyrażoną współczynnikiem Zenera \(A_{\text{Z}} = 2C_{44}/(C_{11}-C_{12})\), a liczbą ziaren \(N_{\text{RVE}}\), niezbędną do uzyskania reprezentatywnego elementu objętościowego przy akceptowalnym poziomie błędu \(\delta\) [1064]: \[\label{eq:Nygards} N_{\text{RVE}} = \frac{k}{\delta^2}\left( A_{\text{Z}} - 1 \right),\] przy czym, współczynnik współczynnik \(k\), zależny jest od zastosowanych obciążeń i wymiarów modelu: w przypadku jednoosiowym dla modelu 3D, \(k=0.033\) [1064]. Pomimo faktu, że zależność ta została wyznaczona empirycznie, na podstawie analiz numerycznych prowadzonych dla układu regularnego, to może być ona użyteczna również w szerszym kontekście, wskazując, jak silnie uzależniony jest rozmiar RVE od anizotropii krystalitów i zakładanego błędu obliczeniowego. W celu wyznaczenia parametrów sprężystych, nawet przy niewielkim poziomie anizotropii krystalitów i akceptowalnym, jednoprocentowym błędzie, konieczne staje się analizowanie układów zawierających setki ziaren.
Ilościową definicję reprezentatywnego elementu objętościowego zaproponował Kanit [982, 1065]. W statystycznym opisie, opartym na symulacjach numerycznych przeprowadzonych dla właściwości sprężystych i przewodności cieplnej dwufazowych polikryształów, uwzględnił on pięć parametrów, które istotnie wpływają na rozmiar RVE: rodzaj analizowanej właściwości fizycznej, ,,kontrast” (niedopasowanie) właściwości fizycznych, udział objętościowy składników, precyzję oszacowania właściwości efektywnych oraz liczbę realizacji mikrostruktury 56. W zwięzłej formie zależność między tymi parametrami a rozmiarem RVE wyrażonym objętością \(V_{\text{RVE}}\) można przedstawić równaniem [982, 1065]: \[\label{eq:KanitVRVE} V_{\text{RVE}} = \left( \frac{4}{\delta_{\text{abs}}^2 n} \mathrm{D}_Z^2 \right)^{\!1/\alpha}\!\! \mathcal{A},\] w którym \(\mathrm{D}_Z^2\) jest wariancją estymowanej właściwości fizycznej \(Z\), \(\delta_{\text{abs}}\) – akceptowalną wartością błędu bezwzględnego wyznaczenia tej właściwości, oraz \(n\) – liczbą realizacji, dla których przeprowadzane są symulacje.
Parametry \(\alpha\) oraz \(\mathcal{A}\) w równaniu \eqref{eq:KanitVRVE}, są parametrami skalowania, wiążącymi wariancję \(\mathrm{D}_Z^2\) z objętością analizowanej przestrzeni \(V\) i muszą zostać ustalone w trakcie procedury kalibracyjnej. Procedura taka opiera się na serii realizacji utworzonych dla kilku różnych rozmiarów \(V\). Dla takich niezależnych realizacji, w trakcie symulacji wstępnych, wyznaczane są wartości analizowanych właściwości pozornych \(Z\), a następnie dla poszczególnych \(V\), obliczane są wartości średnie oraz wariancje. W kolejnym kroku, do uzyskanych danych, dopasowywane jest równanie skalowania [982]: \[\label{eq:KanitDZV} \mathrm{D}_Z^2(V) = V_V(1-V_V)(Z_1 - Z_2)^2 \left(\frac{\mathcal{A}}{V}\right)^{\!\alpha}\!,\] w którym \(V_V\) jest udziałem objętościowym wybranego składnika, a \(Z_1\) i \(Z_2\) są wartościami analizowanych właściwości, odpowiednio dla fazy pierwszej i drugiej. Uzyskane na podstawie dopasowania parametry \(\alpha\) oraz \(\mathcal{A}\), mogą ostatecznie zostać użyte w równaniu \eqref{eq:KanitVRVE} do oszacowania rozmiaru RVE.
Przedstawiona, numeryczna definicja RVE zaproponowana przez Kanita, stanowi przykład podejścia statystycznego, które zdominowało rozwiązania stosowane w symulacjach mikromechanicznych opartych na modelach mikrostruktury [1066–1069]. Dodatkowo, Kanit wykazał również, że poprzez homogenizację przeprowadzoną dla pewnej liczby realizacji (zespołu) o rozmiarach okna mikrostrukturalnego mniejszych od RVE, możliwe jest uzyskanie wartości pozornej dla estymowanej właściwości, zgodnej z wartością efektywną w granicach przyjętej dokładności. Wymiary przestrzenne realizacji składających się na taki zespół, są jednak również istotne. Dla zbyt małych objętości, wpływ efektów deterministycznych wynikających np. z oddziaływań występujących na granicach modelu (efektów brzegowych), nie może zostać wyeliminowany poprzez uśrednianie.
Drugan i Willis [1048], obliczyli dla rozpatrywanego przez nich kompozytu ziarnistego, że rozmiar RVE niezbędny do osiągnięcia wartości efektywnego modułu sprężystości z maksymalnym błędem na poziomie 1 %, jest jedynie \(\sim\)4.5 raza większy od średnicy wtrąceń.↩︎
Realizacja oznacza tutaj niezależny model geometryczny, wirtualną mikrostrukturę, na której jest przeprowadzana symulacja.↩︎
Podstawowe, teoretyczne wymagania, co do rozmiaru RVE – na tyle dużego, aby zawierał on wystarczającą liczbę szczegółów mikrostruktury, zapewniał reprezentację budowy całego materiału i ograniczał wpływ przemieszczeń i obciążeń obecnych na brzegach modelu na globalne wartości pozorne – są trudne, a często wręcz niemożliwe do spełnienia [1036, 1070, 1071]. Duży rozmiar i szczegółowość (rozdzielczość) modelu geometrycznego, odpowiadającego warunkom RVE, sprawia, że koszt obliczeniowy staje się w praktyce nie do przyjęcia. Ponadto, wykorzystywane w symulacjach syntetyczne mikrostruktury, z założenia, tylko statystycznie odpowiadają rzeczywistej topologii i morfologii materiału. Dlatego w modelowaniu ośrodków niejednorodnych rozpowszechniła się koncepcja wykorzystująca symulacje prowadzone na zespole realizacji, których rozmiary są mniejsze od RVE, ale przy zakładanym poziomie dokładności, umożliwiają uzyskanie właściwości efektywnych [590, 771, 949, 968, 1045, 1048, 1053, 1063, 1070–1077]. Takie podejście opiera się na hipotezie ergodyczności, która zakłada, że dla stochastycznych ośrodków niejednorodnych średnia wyznaczona dla pojedynczej objętości RVE, odpowiada średniej dla odpowiednio dużego zespołu realizacji, nawet jeśli niezależnie nie są one reprezentatywne [218, 983].
Zastąpienie pojedynczego modelu geometrycznego, opisującego pełny zakres zmienności wszystkich istotnych cech mikrostruktury, wieloma mniejszymi reprezentacjami, powoduje znaczące obniżenie wymagań dotyczących mocy obliczeniowej. Prowadzi to również do przyspieszenia analiz numerycznych poprzez wykorzystanie obliczeń równoległych (ang. parallel computing) [1036, 1077]. Zastosowanie zespołu niezależnych realizacji, pozwala dodatkowo na uwzględnienie, z natury stochastycznych, właściwości materiału. Podejście to, wymaga jednak przeformułowania założeń dotyczących reprezentatywności rozpatrywanego układu niejednorodności. W rozwiązaniach numerycznych opartych na zespole realizacji, RVE jest więc zastępowany statystycznym (stochastycznym) elementem objętościowym (SVE, ang. Statistical Volume Element) [590, 1045, 1048, 1053, 1063, 1073].
Statystyczny element objętościowy, należy więc traktować raczej jako zespół wielu niezależnych realizacji o rozmiarach \(V_{\text{SVE}}\) (przy czym \(V_{\text{SVE}}\) < \(V_{\text{RVE}}\)) i liczebności \(n_{\text{SVE}}\), na tyle duży, aby zawierał przynajmniej tyle informacji mikrostrukturalnych, co RVE. Pojedyncza realizacja jest więc specyficzną, niejednorodną próbką materiału, będącą jedną z możliwych reprezentacji jego mikrostruktury i podlegającą deterministycznym prawom mechaniki klasycznej [983, 1045]. Uśrednianie wartości pozornych uzyskanych z takich niezależnych realizacji, w obrębie całego zespołu, pozwala zatem na estymowanie wartości efektywnej, przy czym ich rozrzut (niepewność pomiarowa) będzie zmniejszał się wraz ze wzrostem liczby realizacji (\(n_{\text{SVE}}\)) i ich objętości (\(V_{\text{SVE}}\)) [1078] (rys. 3.5). Jakość oszacowania wyrażana jest błędem standardowym (\(\delta_{\text{SVE}} = 2s/\sqrt{n_{\text{SVE}}}\)) [1065], przedziałem ufności przy przyjętym poziomie istotności (\(\delta_{\text{SVE}} = t_{n,\alpha} \delta_{\text{rel}}/\sqrt{n_{\text{SVE}}}\)) [771, 1067], albo jest ustalana na podstawie innych, statystycznych deskryptorów rozkładu np. funkcji korelacji \(n\)-punktowej [598, 1079].
Ograniczanie kosztów obliczeniowych, które w oczywisty sposób premiuje użycie jak najmniejszego zespołu realizacji, a z drugiej strony konieczność uwzględnienia lokalnych zaburzeń (np. mikropęknięć, wytrąceń), występujących w stochastycznych ośrodkach niejednorodnych, powodują, że intensywnie prowadzone są badania nad opracowaniem kryteriów numerycznych dla SVE [771, 931, 1069, 1080].
Najbardziej intuicyjne kryterium określające statystyczny element objętościowy, podobnie jak w przypadku RVE, opiera się na rozmiarze analizowanej przestrzeni. Rozmiar taki, może zostać wyrażony poprzez stosunek wymiarów charakterystycznych dla skal \(L/D\) (zob. rys. 3.3), albo poprzez liczbę niejednorodności zawartych w rozpatrywanej objętości \(n_{\text{w}}\). Opierając się na regułach przyjętych w mechanice ciała stałego [983, 1081], stosunek \(L/D\) powinien zawierać się w przedziale od 10 do 100, w zależności od rozpatrywanego zagadnienia i rodzaju materiału. Przy okazji warto zauważyć, że im stosunek ten jest większy (w granicy \(L/D \rightarrow \infty\)), tym rozmiar SVE coraz bardziej zbliża się do rozmiaru RVE. W przypadku arbitralnie przyjętego rozmiaru SVE, liczba niezależnych realizacji \(n_{\text{SVE}}\) jest zwykle dobierana tak, aby uzyskać zadowalającą dokładność oszacowania wartości efektywnej.
Opierając się na parametrach mikrostruktury, rozmiar SVE może być również dobrany na podstawie statystycznych deskryptorów rozkładu przestrzennego. W tym celu wykorzystywana jest najczęściej, opisana już wcześniej, funkcja korelacji dwupunktowej (zob. p. 2.2.5). Na jej podstawie wyznaczany jest promień korelacji, który służy do określenia rozmiaru SVE [218, 577, 598, 949, 1036, 1082–1085]. Metoda ta pozwala na ustalenie rozmiaru SVE już na etapie przygotowania modelu geometrycznego. W porównaniu z metodami opierającymi się na kolejnych, opisanych poniżej kryteriach, takie podejście znacząco ogranicza liczbę realizacji niezbędnych do oszacowania rozmiaru SVE.
Zazwyczaj jednak, w kryteriach numerycznych, wykorzystywane są wyniki uzyskane w szeregu symulacji, na podstawie których a posteriori ustalany jest rozmiar SVE, pozwalający na uzyskanie zadowalającej dokładności estymacji właściwości efektywnych. Jedno z takich kryteriów, opiera się na relacji \eqref{eq:HuetC} \eqref{eq:HuetS} wyprowadzonej przez Hueta [1049]. Zwiększając sukcesywnie rozmiar analizowanego okna mikrostrukturalnego, porównywane są wartości pozorne uzyskiwane dla kolejnych zespołów realizacji, przy zastosowaniu różnych warunków brzegowych (zob. rys. 3.4). W najprostszym podejściu stosowane są kinematyczne (KUBC) i statyczne (SUBC) warunki brzegowe, które pozwalają określić granice oszacowania. Rozmiar okna mikrostrukturalnego, przy którym rozpiętość tych granic osiągnie wartość akceptowalną (mniejszą niż zakładany błąd oszacowania) przyjmowany jest za SVE.
Szczegółowe omówienie teoretyczne wpływu różnego rodzaju warunków brzegowych, kształtu niejednorodności i analizowanych właściwości termomechanicznych na jakość oszacowania granic właściwości efektywnych, zostało zawarte w pracach Ostoji-Starzewskiego [983, 1045]. Wyniki tych prac wskazują, że w przypadku stochastycznego medium, jakiego przykładem jest jedno i wielofazowy materiał polikrystaliczny, w którym nie występuje okresowość budowy, rozmiar SVE nie może zostać określony dokładnie. W takim razie, należy raczej opierać się na przybliżonych oszacowaniach SVE uzyskanych metodami mikromechaniki obliczeniowej, specyficznych dla konkretnego materiału i rozpatrywanej właściwości [949, 1086, 1087].
Kolejna metoda wykorzystywana do określania rozmiaru SVE, opiera się na kryterium stabilizacji właściwości pozornych [1003, 1069, 1083]. W odróżnieniu od poprzedniej metody, analizie poddawane są tutaj wyniki symulacji przeprowadzonych dla zespołu realizacji, jedynie dla wybranego typu warunków brzegowych. Ponieważ szybkość konwergencji właściwości pozornych, zmieniająca się wraz ze wzrostem rozmiaru analizowanego okna mikrostrukturalnego, zależy od kształtu niejednorodności, rozpatrywanej właściwości oraz od zastosowanych warunków brzegowych [1078], to metoda ta opiera się również na analizie wyników a posteriori. Rozmiar okna mikrostrukturalnego, przy którym względna różnica pomiędzy wartościami pozornymi wyznaczonymi w kolejnych zespołach, stabilizuje się i jest mniejsza od założonego kryterium, wyznacza SVE 57. Z uwagi na możliwość wystąpienia fluktuacji właściwości pozornych, warunek stabilizacji sprawdza się najlepiej w przypadku niewielkich zaburzeń analizowanego pola właściwości termomechanicznych oraz dla prostej, regularnej mikrostruktury np. w przypadku kompozytów ziarnistych o izometrycznych izolowanych wtrąceniach.
Najbardziej rozpowszechnione metody wyznaczania SVE, opierają się jednak na kryteriach łączonych – numeryczno-statystycznych. Wyniki symulacji, uzyskane dla modeli geometrycznych o różnych rozmiarach i liczebności, opracowywane są statystycznie i, na tej podstawie, wyznaczany jest rozmiar SVE. Stosowane tutaj kryteria wykorzystują niepewność pomiarową numerycznego wyznaczenia wartości pozornych. Przyjmuje się, że aby analizowany rozmiar okna mikrostrukturalnego spełniał warunek reprezentatywności, niepewność numeryczna, musi mieścić się w przyjętym z góry zakresie tolerancji.
Jak już wcześniej wspomniano, niepewność taka, określająca jakość oszacowania, może zostać wyrażona błędem standardowym. W przypadku gdy analizie statystycznej podlega duża liczba realizacji \(n\) i dodatkowo wyznaczona zostaje zależność funkcyjna pomiędzy wariancją \(\mathrm{D}_Z^2(V)\) estymowanej właściwości \(Z\) a rozmiarem okna mikrostrukturalnego \(V\), wykorzystany może zostać warunek [982, 1065]: \[\label{eq:krytVar} \delta_{\text{rel}} = \frac{\delta_{\text{abs}}}{\langle Z \rangle} = \frac{2\mathrm{D}_Z}{\langle Z \rangle \sqrt{n}} \leqslant \delta_{\text{tol}},\] w którym \(\delta_{\text{rel}}\) i \(\delta_{\text{abs}}\), są niepewnościami numerycznymi wyznaczenia właściwości pozornych, odpowiednio względną oraz bezwzględną, \(\langle Z \rangle\) jest średnią arytmetyczną wartości pozornych uzyskanych w kolejnych \(n\) realizacjach, a \(\delta_{\text{tol}}\) wartością dopuszczalnego błędu (tolerancji) wyznaczenia wartości efektywnej \(Z^{*}\). W warunku tym, \(\mathrm{D}_Z\), będąca pierwiastkiem kwadratowym z wariancji wartości \(Z\), uzyskanych przy rozpatrywanym rozmiarze okna mikrostrukturalnego \(V\), określana jest przy pomocy zależności semi-analitycznych. Przykładem takich zależności dla właściwości liniowych jest równanie \eqref{eq:KanitDZV} wyprowadzone przez Kanita [982, 1065], które zostało rozszerzone przez Pelissou i in. [1067] dla właściwości nieliniowych (np. kruchego pękania). Kalibracja takich równań, poprzez dopasowanie ich do wyników symulacji (dobranie wartości parametrów numerycznych), wymaga jednak rozległych analiz prowadzonych dla kilku rozmiarów okien mikrostrukturalnych przy odpowiednio dobranej liczebności zespołów realizacji [982, 1067, 1068, 1088–1090]. Uzyskane w ten sposób zależności pozwalają jednak na późniejsze, szybkie oszacowanie rozmiaru SVE dla określonej mikrostruktury i wybranej właściwości fizycznej.
Ponieważ wyniki kalibracji równań semi-analitycznych mogą zostać powtórnie wykorzystane jedynie dla specyficznych zagadnień (dla określonej właściwości i mikrostruktury), to niekiedy do ustalenia rozmiaru SVE wygodniejsze jest bezpośrednie wykorzystanie testu statystycznego. Jednym ze stosowanych do szacowania rozmiaru SVE testów, jest test \(\chi^2\). Został on zaproponowany przez Gitmana i in. [1066, 1091], do szybkiego wyznaczania rozmiaru SVE na podstawie niewielkiej liczby realizacji i rozmiarów okien mikrostrukturalnych dla kompozytów ziarnistych. W opisanej przez nich procedurze, bazowy rozmiar okna mikrostrukturalnego określany jest na podstawie wymiaru charakterystycznego największych wtrąceń obecnych w analizowanym materiale (\(L = 2D_{\text{max}}\)). Wymiary kolejnych kilku okien są coraz większe, przy czym liczba niezależnych realizacji wewnątrz zespołu \(n \geqslant 5\). Wyznaczone dla takiej próby wartości pozorne wybranego parametru \(Z\), służą następnie do wykonania testu [1066, 1091]: \[\label{eq:GitmanChi} \chi^2 = \sum\limits_{i=1}^{n} \left( \frac{Z_i}{\langle Z \rangle} - 1 \right)^{\!2}\!,\] przy czym \(\langle Z \rangle\) jest średnią wartością pozorną wybranego parametru \(Z\) dla wszystkich realizacji w całej próbie.
Uzyskana z powyższego równania wartość \(\chi^2\), dla kolejnych rozmiarów okien mikrostrukturalnych, zostaje porównana z wartością tablicową dla określonej liczby stopni swobody i przyjętego poziomu istotności testu. Ostatecznie pozwala to na określenie, czy uzyskane wartości nie odbiegają istotnie od średniej dla całej próby i czy rozpatrywany rozmiar okna można traktować jako SVE.
Zaproponowana przez Gitmana i in. [1066, 1091, 1092] procedura opierająca się na określonych arbitralnie rozmiarach analizowanych okien mikrostrukturalnych, na podstawie których wyznaczana jest wartość \(\langle Z \rangle\), może jednak dla niektórych układów (o silnie nieliniowych właściwościach, dużej anizotropii albo przy nieizometrycznych kształtach wtrąceń) prowadzić do zaniżenia estymowanego rozmiaru SVE.
Niepewność numeryczna wyznaczenia wartości pozornych może być również wyrażona przedziałem ufności. Na tej podstawie skonstruowane jest kolejne, często stosowane kryterium, pozwalające na określenie rozmiaru SVE [1009, 1073, 1086, 1087]. Podobnie jak w przypadku analizy wariancji \eqref{eq:krytVar}, przyjmuje się tutaj, że niepewność pomiarowa \(\delta_{\text{rel}}\), musi być mniejsza niż założona dopuszczalna tolerancja wyznaczenia wartości efektywnej \(\delta_{\text{tol}}\). Stosując rozkład t-Studenta, kryterium oparte na przedziale ufności można zapisać równaniem [1009]: \[\label{eq:krytCI} \delta_{\text{rel}} = t_{n-1,1-\alpha/2} \frac{ \delta_{\text{abs}} }{\sqrt{n} \langle Z \rangle} \leqslant \delta_{\text{tol}},\] w którym \(t_{n-1,1-\alpha/2}\) jest zmienną odczytaną z tablic rozkładu t-Studenta przy \(n-1\) stopniach swobody dla zakładanego poziomu ufności \(1-\alpha\), oraz \(\delta_{\text{abs}}\) niepewnością wyznaczenia wartości pozornych \(Z\) w \(n\) realizacjach i zwykle wyrażana jest odchyleniem standardowym.
Procedura wyznaczania rozmiaru SVE z wykorzystaniem powyższego kryterium \eqref{eq:krytCI} również opiera się na sukcesywnym sprawdzaniu warunku dla coraz większych okien mikrostrukturalnych, przy ustalonej, zwykle dużej, liczbie realizacji. Uzyskanie wartości \(\delta_{\text{rel}}\) mniejszej niż zakładany, dopuszczalny poziom tolerancji, oznacza osiągnięcie rozmiaru okna odpowiadającego założeniom SVE.
Oprócz kryteriów wykorzystujących niepewność pomiarową numerycznego wyznaczenia wartości pozornych, do oceny rozmiaru SVE można zastosować również kryterium oparte na symetrii materiału. W kryterium tym przyjmuje się, że właściwości pozorne uzyskane na podstawie symulacji mikromechanicznych, powinny wykazywać tę samą symetrię, co właściwości materiału w makroskali [1069]. W najprostszym przypadku, dla materiałów makroskopowo izotropowych, oznacza to, że statystyczny element objętościowy powinien wykazywać izotropię rozpatrywanej właściwości fizycznej bez względu na wewnętrzną symetrię budujących go elementów składowych.
W odniesieniu do ceramicznych materiałów polikrystalicznych, kryterium oparte na izotropii zespołu niezależnych realizacji, może pozwalać na efektywne oszacowanie rozmiaru SVE [771]. Obserwowana w tych materiałach izotropia makroskopowych właściwości termomechanicznych, jest cechą typową 58, wynikającą z przypadkowej orientacji krystalitów. Odstępstwa od izotropii mogą pojawić się w wyniku celowej modyfikacji mikrostruktury na etapie formowania ,,surowego materiału” (zob. p. 1.3.3), albo mogą być efektem stosowanych technik spiekania (np. prasowania na gorąco, HP ang. Hot Pressing). Pomijając te przypadki, zarówno jedno- jaki i wielofazowe polikryształy ceramiczne, otrzymywane poprzez spiekanie swobodne, są makroskopowo izotropowe. Zatem odstępstwo od izotropii może być miarą pozwalającą na oszacowanie rozmiaru SVE.
Ren i Zheng [1053, 1063] oraz Nygårds [1064], analizując zależność między anizotropią właściwości sprężystych krystalitów z układu regularnego a liczbą ziaren niezbędną do uzyskania właściwości efektywnych dla materiałów polikrystalicznych, zauważyli, że zależność ta jest w przybliżeniu liniowa. Ranganathan i Ostoja-Starzewski [1093], opierając się na funkcji skalowania, łączącej anizotropię pojedynczego krystalitu o strukturze regularnej z rozmiarem okna mikrostrukturalnego, zaproponowali metodą określania rozmiaru SVE dla właściwości liniowo-sprężystych w polikryształach o stochastycznej mikrostrukturze. Funkcję tę wykorzystali również do określenia rozmiaru SVE dla przewodności cieplnej krystalitów z układu regularnego, trygonalnego, heksagonalnego i tetragonalnego [1094]. Funkcja skalowania dla krystalitów z układu regularnego, została zastosowana także przez Tenreiro Vieirę i in. [1095]. Opracowany przez nich współczynnik anizotropii opierał się na odchyleniu standardowym modułu Younga, wyznaczonym dla zespołu realizacji. Na jego podstawie zaproponowali oni zależność pozwalającą na wyznaczenie rozmiaru SVE dla polikryształów zbudowanych z krystalitów należących do układu regularnego.
Kryterium izotropii zespołu niezależnych realizacji zostało wykorzystane również do szacowania rozmiaru SVE dla kompozytu zawierającego włókna krótkie o losowej orientacji w przestrzeni. Moussaddy i in. [1069], do wyznaczenia odstępstwa od izotropii, wykorzystali macierz niepewności dla zespołu niezależnych realizacji. Została ona skonstruowana w oparciu o różnice względne, obliczane dla wszystkich współczynników w sztywności \(C_{\alpha\beta}\) rozpatrywanego kompozytu, w odniesieniu do odpowiednich współczynników sztywności dla materiału izotropowego. W celu określenia rozmiaru SVE, Moussaddy i in. [1069] posłużyli się procedurą składającą się z dwóch etapów. W pierwszym, dla wybranego rozmiaru okna mikrostrukturalnego, ustalana była liczba realizacji \(n\). Dla kolejnych, generowanych w trakcie wirtualnego eksperymentu, syntetycznych mikrostruktur, na podstawie kryterium \eqref{eq:krytCI}, sprawdzana była niepewność numeryczna wyznaczenia modułu ściśliwości \(\mathcal{K}\). Jeśli liczba przeanalizowanych realizacji \(n\), zapewniała osiągniecie ustalonej tolerancji wyznaczenia wartości efektywnej (\(\delta_{\text{rel}} \leqslant \delta_{\text{tol}}\)), to w etapie drugim, wykorzystując macierz niepewności, sprawdzany był dodatkowo warunek izotropii. Jeśli na tym etapie maksymalna wartość względnej różnicy współczynników sztywności w macierzy niepewności nie przekraczała przyjętego poziomu błędu, to taki zestaw \(n\) realizacji, zawierający \(N\) włókien, spełniał kryteria statystycznego elementu objętościowego.
Praca Moussaddy’ago i in. [1069] jest jedną z nielicznych, w których problem dotyczący liczby niezależnych realizacji w zespole jest kluczowy przy szacowaniu rozmiaru SVE. Zazwyczaj, liczba ta przyjmowana jest arbitralnie, a badany jest głównie wpływ rozmiaru okna mikrostrukturalnego wyrażonego poprzez objętość przestrzeni (\(V_{\text{SVE}}\)) albo liczebność niejednorodności \((N_{\text{SVE}})\), na możliwość osiągnięcia właściwości efektywnych.
Inne podejście do szacowania rozmiaru SVE dla kompozytu włóknistego, opierające się jednak na kryterium izotropii, zostało przedstawione przez López Jiménez [1096]. W pracy wykorzystana została bezpośrednia analiza wpływu kierunku działania obciążeń na makroskopową odpowiedź modelu. Na podstawie szeregu symulacji, w których wyznaczona została wartość modułu sprężystości poprzecznej przy różnych wartościach kąta działania obciążeń (\(\mathcal{G}_{\theta}\)), López Jiménez zauważył, że wraz ze wzrostem rozmiaru okna mikrostrukturalnego, rozrzut uzyskiwanych wartości \(\mathcal{G}_{\theta}\), wyrażony poprzez współczynnik zmienności \(\upsilon_{\mathcal{G}} = s_{\mathcal{G}}/\langle \mathcal{G}\rangle\), maleje. Obserwacja ta jest w pełni zbieżna z wynikami wcześniej opisanych procedur opartych na kryterium izotropii, jednak zastosowane podejście jest łatwe do implementacji w modelach numerycznych wykorzystujących wirtualną mikrostrukturę.
Na podobnej analizie, oparte jest również autorskie opracowanie problemu dotyczącego określenia rozmiaru SVE [771]. Pierwotnie zostało ono wykorzystane w symulacjach rozszerzalności cieplnej polikryształów trygonalnego \(\alpha\text{-Al}_{\text{2}}\text{O}_{\text{3}}\), tetragonalnego \(\beta\text{-ZrO}_{\text{2}}\) stabilizowanego 3-molowym dodatkiem \(\text{Y}_{\text{2}}\text{O}_{\text{3}}\) (3Y-TZP) oraz kompozytów ziarnistych z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)–3Y-TZP [771]. Później, opracowana metodyka, została zastosowana także w symulacjach resztkowych naprężeń cieplnych obecnych w polikrystalicznym heksagonalnym \(\beta\text{-Si}_{\text{3}}\text{N}_{\text{4}}\) o silnie wydłużonych ziarnach i jego kompozytach (\(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) i \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\)) [178, 1097]. Symetria sieci krystalicznej tych materiałów sprawia, że zarówno rozszerzalność cieplna jak i właściwości sprężyste krystalitów wykazują wyraźną anizotropię, natomiast makroskopowe właściwości litych tworzyw, otrzymywanych poprzez spiekanie swobodne, są praktycznie izotropowe.
W zaproponowanej procedurze wyznaczania rozmiaru SVE, główna uwaga skierowana została na wyznaczenie liczby niezależnych realizacji \(n_{\text{SVE}}\) w zespole o ustalonej objętości – rozmiarze okna mikrostrukturalnego \(V_{\text{SVE}}\). Takie odwrócone podejście nie jest typowe wśród stosowanych rozwiązań. W praktyce jednak, pozwala na istotne ograniczenie zakresu analiz niezbędnych do ustalenia rozmiaru SVE. Przyjęcie a priori rozmiaru okna mikrostrukturalnego, jest w istocie podejściem analogicznym do stosowanego często w badaniach doświadczalnych. W obserwacjach mikroskopowych, czy doświadczalnych metodach rekonstrukcyjnych, rozmiar badanej przestrzeni jest dobierany na drodze kompromisu pomiędzy wymaganą szczegółowością a możliwościami technicznymi: rozdzielczością, czasem pomiarowym, a nawet rozmiarem danych uzyskiwanych w takich pomiarach. Z kolei w analizach mikromechanicznych, opierających się na rzeczywistych mikrostrukturach, rozmiar modelu geometrycznego jest ograniczony z góry rozmiarem dostępnych danych doświadczalnych (objętością zrekonstruowanej mikrostruktury czy rozmiarem obrazów mikroskopowych). Dla metod wykorzystujących syntetyczne mikrostruktury, rozmiar analizowanej przestrzeni również nie może być dowolnie duży. W praktyce istotnym ograniczeniem jest ilość danych wymaganych do opisu geometrii modelu oraz rozmiar modelu obliczeniowego i uzyskanych na jego podstawie wyników symulacji. Dlatego, opierając się na wynikach cytowanych już prac (np. [982, 983, 1053, 1064, 1077, 1080, 1094, 1098]), dla wielu materiałów polikrystalicznych i kompozytowych, można ustalić przybliżony rozmiar SVE (objętość okna mikrostrukturalnego \(V_{\text{SVE}}\) albo liczebność ziaren \(N_{\text{SVE}}\)), spełniający podstawowe wymagania odnośnie reprezentatywności i jednocześnie uwzględniający ograniczenia numeryczne.
Analizując zatem właściwości pozorne uzyskane z symulacji prowadzonych dla zespołu realizacji o przyjętym rozmiarze SVE, można przyjąć, że jeśli przy ustalonym poziomie tolerancji, wartości właściwości wyznaczanych w różnych kierunkach przestrzeni modelu będą sobie równe, to na podstawie kryterium izotropii, właściwości te można uznać za właściwości efektywne. Oczywiście, do takiego ujednorodnienia może dojść jedynie, gdy porównywane będą wartości uzyskane z odpowiednio licznego zespołu realizacji \(n_{\text{SVE}}\).
W celu ustalenia wymaganej liczebności \(n_{\text{SVE}}\) można przyjąć, że miarą odstępstwa od postulowanej izotropii będzie rozrzut wartości odkształceń, wyznaczanych dla trzech kierunków głównych modelu geometrycznego \(\varepsilon_x\), \(\varepsilon_y\), \(\varepsilon_z\), wywołanych jednorodnym obciążeniem 59. Rozrzut ten można wyrazić poprzez ogólną wariancję powtarzalności na podstawie wartości \(\varepsilon_{ij}\) obliczonych w kolejnych \(n\) realizacjach (\(i = 1,\dots,n\)) dla trzech kierunków (\(m = 3\), \(j = 1,\dots,m\)) [1099]: \[\label{eq:tot_var} s_{\varepsilon}^2 = \frac{\displaystyle \sum_{i=1}^{n} \sum_{j=1}^{m} \left( \varepsilon_{ij} - \bar{\varepsilon}_i\right)^2}{n ( m - 1 )},\] przy czym \(\bar{\varepsilon}_i\) jest średnią arytmetyczną z wartości odkształceń wyznaczonych dla \(i\)-tej realizacji \(\bar{\varepsilon}_i = \frac{1}{3} \left(\varepsilon_{ix} + \varepsilon_{iy} + \varepsilon_{iz} \right)\), a pozorne, izotropowe odkształcenie modelu \(\varepsilon^{\text{app}}\), dane jest wartością średnią dla wszystkich \(n\) realizacji: \[\label{eq:eps_app} \varepsilon^{\text{app}} = \frac{1}{n} \displaystyle \sum_{i=1}^{n} \bar{\varepsilon}_i.\] Korzystając z jednostronnego testu Chi-kwadrat, można następnie ustalić granicę maksymalnego błędu bezwzględnego \(\delta_{\text{abs}}^{\text{app}}\), popełnianego przy wyznaczeniu wartości pozornej dla założonego poziomu istotności \(\alpha\) i \(f\) stopni swobody (\(f = n ( m - 1 )\)): \[\label{eq:error_abs} \delta_{\text{abs}}^{\text{app}} \leqslant \sqrt{ \frac{f \, s_{\varepsilon}^2}{\chi_{\alpha}^2} }\] oraz błąd względny \(\delta_{\text{rel}}^{\text{app}} = \delta_{\text{abs}}^{\text{app}}/\varepsilon^{\text{app}}\).
Tak określona niepewność wyznaczenia właściwości pozornych, pozwala na oszacowanie liczby niezależnych realizacji \(n_{\text{SVE}}\), zapewniającej osiągnięcie wartości efektywnej przy zakładanym poziomie ufności. W tym celu można oprzeć się na klasycznej metodzie doboru minimalnej liczebności próby statystycznej. Ponieważ dla dużych modeli geometrycznych wymagana liczba realizacji \(n_{\text{SVE}}\) może być mniejsza od 30 (mała próba), to do ustalenia liczebności próby można wykorzystać rozkład t-Studenta i odpowiednią zależność wyrazić równaniem: \[\label{eq:n_sve} n_{\text{SVE}} \geqslant \left( t_{f,1-\alpha/2} \frac{\delta_{rel}^{app}}{\delta_{\text{tol}}}\right)^{\!2}\!\!,\] w którym \(t_{f,1-\alpha/2}\) jest wartością odczytaną z tablic rozkładu t-Studenta dla \(f\) stopni swobody i zakładanym poziomie ufności \(1 - \alpha/2\).
W praktyce cała procedura pozwalająca na wyznaczenie liczebności niezależnych realizacji przy określonym rozmiarze okna mikrostrukturalnego, może zostać przeprowadzona w kilku krokach:
wykonanie analiz numerycznych dla niewielkiej liczby pilotażowych realizacji (np. \(n = 5\)),
obliczenie dla nich wariancji \(s_{\varepsilon}^2\) \eqref{eq:tot_var} i wartości \(\varepsilon^{\text{app}}\) \eqref{eq:eps_app},
wyznaczenie błędu bezwzględnego \(\delta_{\text{abs}}^{\text{app}}\) \eqref{eq:error_abs} i względnego \(\delta_{\text{rel}}^{\text{app}}\),
wyznaczenie liczby realizacji \(n_{\text{SVE}}\) \eqref{eq:n_sve},
wykonanie analiz numerycznych dla wyznaczonej \(n_{\text{SVE}}\),
weryfikacja poprawności wyznaczenia \(n_{\text{SVE}}\).
Weryfikację poprawności wyznaczenia \(n_{\text{SVE}}\) należy przeprowadzić poprzez porównanie wartości błędu względnego \(\delta_{\text{rel}}^{\text{app}}\), obliczonego na podstawie pilotażowych realizacji (\(n = 5\)) w kroku [a3], z wartością błędu względnego \(\Delta_{\text{rel}}^{\text{app}}\), obliczoną dla wszystkich przeanalizowanych realizacji (\(n = n_{\text{SVE}}\)). Przy docelowej liczbie realizacji większej od liczby realizacji pilotażowych (\(n_{\text{SVE}} > n\)), można oczekiwać zmniejszenia wartości błędu względnego (stabilizacja wartości średniej) i zazwyczaj \(\Delta_{\text{rel}}^{\text{app}} < \delta_{\text{rel}}^{\text{app}}\). Jednak w przypadku dużej anizotropii rozpatrywanej właściwości fizycznej pojedynczych krystalitów oraz niewielkiego rozmiaru okna mikrostrukturalnego, relacja ta może być odwrotna. W takim przypadku, na podstawie równania \eqref{eq:n_sve} należy ponownie wyznaczyć \(n_{\text{SVE}}\), wykorzystując niepewność pomiarową wyrażoną wartością \(\Delta_{\text{rel}}^{\text{app}}\). Opisywaną procedurę można również przeprowadzać sukcesywnie, na podstawie wyników kolejnych przeprowadzonych analiz, i w ten sposób, na bieżąco kontrolować wartość błędu wyznaczenia właściwości efektywnej oraz wynikającą z niego liczbę realizacji.
Przedstawiona procedura pozwala na istotne ograniczenie liczby niezależnych realizacji, które muszą zostać uwzględnione przy wyznaczaniu wartości efektywnych. Zakładając wartość dopuszczalnej niepewności wyznaczenie wartości efektywnej \(\delta_{\text{tol}} = 0.01\), przy poziomie ufności wynoszącym 0.95, wyznaczona liczba \(n_{\text{SVE}}\) wynosi około kilkunastu realizacji, dla których błąd względny \(\delta_{\text{rel}}^{\text{app}} \approx 0.01\). Dla struktur polikrystalicznych, taką wartość błędu wynikającego z odstępstwa od izotropii, można osiągnąć już dla objętości \(V_{\text{SVE}}\) zawierającej populację kilkuset krystalitów. Wygenerowanie syntetycznych mikrostruktur albo zebranie danych doświadczalnych umożliwiających szereg rekonstrukcji o takim rozmiarze, nie stanowi aktualnie bariery technicznej i tym samym pozwala na przewidywanie różnych właściwości materiałowych z niepewnością na poziomie typowego błędu doświadczalnego [771].
Wymienione kryteria numeryczne i statystyczne oraz oparte na nich procedury wyznaczania rozmiaru SVE, zostały przywołane w celu zilustrowania jednego z kierunków, w których prowadzone są prace w zakresie modelowania właściwości tworzyw polikrystalicznych i kompozytowych – stochastycznych ośrodków niejednorodnych oraz takich, w których występuje uporządkowanie średniego i dalekiego zasięgu. Są one jednak istotne również w kontekście badań doświadczalnych, w których rozmiar rozpatrywanego elementu przestrzeni ma zasadnicze znaczenie dla reprezentatywności pomiarów. Wybór kryterium, jest więc podyktowany najczęściej względami praktycznymi, wynikającymi z rodzaju rozpatrywanego zagadnienia, dostępnych danych dotyczących budowy wewnętrznej materiału i stosowanej metody obliczeniowej czy badawczej. Dlatego równolegle rozwijane są również inne techniki, bazujące bezpośrednio na danych pomiarowych, pozwalające na wyznaczenie rozmiaru reprezentatywnego elementu objętościowego, który może zostać wykorzystany zarówno w pracach obliczeniowych jak i doświadczalnych. Można tutaj wymienić chociażby pracę Koohbora i in. [1100], w której na podstawie porównania odkształceń globalnych z uśrednionymi odkształceniami lokalnymi, wyznaczonymi metodą cyfrowej korelacji obrazu (DIC, zob. p. 1.4.2), ustalany jest rozmiar RVE. Analiza obrazu została również wykorzystana w pracy Tu i in. [600]. Autorzy w oparciu o dwuwymiarowe projekcje zawierające dane zebrane w obserwacjach SEM oraz pomiarach EBSD, zaproponowali metodykę pozwalającą na generowanie trójwymiarowych, syntetycznych mikrostruktur, odpowiadających statystycznym kryteriom reprezentatywności. Inne ciekawe rozwiązanie, zostało zaproponowane także przez Scherffa i in. [1071]. W pracy, do wyznaczenia rozmiaru RVE, zostały wykorzystane pomiary twardości przeprowadzone metodą wgłębnikową. Autorzy oparli się na fakcie, że wraz ze wzrostem rozmiaru strefy odkształceń, wywołanej działaniem coraz większego nacisku przykładanego do wgłębnika, rozrzut uzyskiwanych wartości twardości zmniejsza się. Analiza odchylenia standardowego uzyskanych wartości twardości, pozwoliła im na wyznaczenie rozmiaru RVE, który następnie wykorzystali w symulacjach numerycznych. Wymienione prace, potwierdzają więc ogólną tezę, że temat dotyczący reprezentatywności jest wciąż istotny, niezależnie od celu i sposobu prowadzonych badań nad właściwościami materiałów.
Metoda ta stosowana jest również do optymalizacji rozmiaru siatki w MES/FEM.↩︎
W przypadku materiałów metalicznych, kompozytów włóknistych, materiałów gradientowych oraz laminatów, izotropia jest nie jest cechą typową i makroskopowo mogą one wykazywać właściwości anizotropowe – przybliżane modelami: transwersalnie izotropowym albo ortotropowym.↩︎
Oryginalnie [771], do wyznaczenia odstępstwa od izotropii, zastosowane zostały wartości liniowych współczynników rozszerzalności cieplnej wyznaczone dla trzech kierunków modelu: \(\alpha_x\), \(\alpha_y\), \(\alpha_z\).↩︎
Dla wielu zjawisk fizykochemicznych, precyzja i dokładność wyników uzyskiwanych w aktualnie prowadzonych symulacjach numerycznych, umożliwia wykorzystanie ich jako danych referencyjnych w badaniach doświadczalnych. Z jednej strony dotyczy to danych uzyskiwanych na podstawie metod ab initio, a z drugiej, wyników symulacji prowadzonych w makroskali metodami MES/FEM czy CFD. Rosnąca moc obliczeniowa oraz jej dostępność, ale przede wszystkim rozwój specjalistycznego oprogramowania (CAD/CAM, ang. Computer Aided Design/Computer Aided Manufacturing), sprawiły, że metody numeryczne są powszechnie wykorzystywane do projektowania i optymalizacji konstrukcji w inżynierii mechanicznej i lądowej oraz procesów w inżynierii chemicznej. Opisane w poprzednich punktach łączenie skal, stosowane w obliczeniowej inżynierii materiałowej, pozwala również na prowadzenie zaawansowanych analiz, dotyczących zachowania materiału poddawanego różnorodnym obciążeniom: zarówno mechanicznym, cieplnym, elektrycznym, jak i wynikającym z działania czynników chemicznych oraz oddziaływań sprzężonych, wywołanych jednoczesnym działaniem kilku czynników. Dokładność takich przewidywań, osiąganych na podstawie modeli mikromechanicznych wykorzystujących zrekonstruowane bądź syntetyczne mikrostruktury, dla wielu zagadnień jest już porównywalna z dokładnością wyników uzyskiwanych metodami doświadczalnymi [771, 899, 1101–1103].
Badania prowadzone metodami numerycznymi, określanie są niekiedy mianem badań in silico. Termin ten, użyty już wcześniej w kontekście rekonstrukcji mikrostruktury (zob. p. 2.6.1), ma źródło w badaniach biologicznych i medycznych, w których przez analogię do określeń in vivo i in vitro, zastosowany został do ogólnego ujęcia wszystkich metod badawczych prowadzonych przy pomocy komputerów. W takim znaczeniu jest on również stosowany w inżynierii materiałowej [298, 989, 1076, 1104, 1105]. Badania in silico, wpisują się zatem w ogólniejszą koncepcję wirtualnego laboratorium, w którym symulowane mogą być wszystkie etapy pracy nad materiałem: od projektowania właściwości, doboru substratów i metod syntezy, poprzez proces otrzymywania, aż do badania właściwości gotowego tworzywa [1106–1108]. Wszystkie elementy takiego procesu badawczego, są w myśl tej koncepcji, prowadzone metodami in silico. W przypadku poszukiwania nowych tworzyw, takie wirtualne laboratorium może stanowić alternatywę dla klasycznej ścieżki doświadczalnej. Jeśli nawet nie wszystkie etapy pracy możliwe są aktualnie do zrealizowania in silico, to już częściowe włączenie do prac badawczych wybranych elementów tej koncepcji, pozwala efektywnie oceniać kierunki prowadzonych poszukiwań i tym samym znacząco ograniczyć koszty oraz przyspieszyć badania.
W przypadku optymalizacji właściwości materiału, prowadzonej poprzez modyfikację jego składu, mikrostruktury oraz parametrów czy metod syntezy, wykorzystanie wirtualnego laboratorium, umożliwia również prowadzenie eksperymentów numerycznych, wykraczających poza zakres warunków i możliwości badawczych dostępnych w ramach posiadanego sprzętu laboratoryjnego i aparatury pomiarowej. Wielokrotne powtarzanie symulacji dla kluczowych etapów procesu otrzymywania, przy niewielkich modyfikacjach parametrów wejściowych, w połączeniu ze zautomatyzowanym przetwarzaniem i analizą uzyskiwanych danych, znacząco wpływa na efektywność prac badawczo-rozwojowych. Wykorzystanie koncepcji wirtualnego laboratorium, oznacza więc zarówno uniezależnienie zakresu badań od aktualnie posiadanego zaplecza technicznego, jak i pozwala na decentralizację prowadzonych prac, poprzez współdziałanie zespołów należących do różnych, często oddalonych od siebie, ośrodków czy jednostek naukowo-badawczych.
Aby w badaniach z zakresu inżynierii materiałowej, możliwe było pełne wykorzystanie potencjału wynikającego z takiego podejścia, niezbędny jest jednak dalszy rozwój i integracja wszystkich elementów opisywanej koncepcji. Do takich elementów należy przede wszystkim cyfrowy opis materiału oraz standardy i narzędzia służące do wymiany danych między kolejnym etapami prac.
Centralnym elementem koncepcji wirtualnego laboratorium jest cyfrowa reprezentacja materiału (DMR, ang. Digital Material Representation) [913, 1109–1111]. Musi ona zawierać wszystkie charakterystyczne cechy budowy wewnętrznej oraz opisywać właściwości fizyczne rzeczywistego materiału. Dokładne omówienie DMR, ze szczególnym uwzględnieniem polikrystalicznych materiałów metalicznych, można znaleźć w pracach Madeja [786, 1110, 1112]. W pracach tych, wyróżnił on trzy zasadnicze etapy tworzenia DMR, które dobrze ilustrują złożoność zagadnienia. Etap pierwszy, dotyczy więc odtworzenia budowy wewnętrznej materiału, w etapie drugim, DMR uzupełniany jest informacjami o właściwościach fizykochemicznych, a w trzecim, opis przekształcony zostaje do postaci umożliwiającej przeprowadzenie symulacji numerycznych. Etapy te nie są oczywiście od siebie niezależne. Sposób opisu mikrostruktury i właściwości materiału zależy do metody obliczeniowej wykorzystywanej do symulacji rozpatrywanych zjawisk.
Cyfrowa reprezentacja budowy wewnętrznej materiału może zostać utworzona w oparciu o dane doświadczalne albo na podstawie założeń teoretycznych. Na tym etapie wykorzystywane są zatem metody rekonstrukcyjne omówione w podrozdziale 2.4. Uzyskany w taki sposób model geometryczny, powinien opisywać wszystkie elementy mikrostruktury rozpatrywanego materiału. W odniesieniu do polikrystalicznych materiałów ceramicznych, opis taki musi więc uwzględniać w szczególności: kształt krystalitów, obecność fazy międzyziarnowej, wytrąceń, porów, mikrospękań i innych, charakterystycznych dla danego tworzywa, elementów jego budowy wewnętrznej.
Do opisu mikrostruktury przy pomocy trójwymiarowych modeli geometrycznych, stosowane są najczęściej dwa podejścia. Jedno oparte jest na elementach sześciennych – wokselach, a drugie, na siatkach powierzchniowych składających się z płaskich lub wypukłych wielokątów [679, 735, 770, 902, 1111, 1113, 1114]. W przypadku modeli geometrycznych uzyskiwanych metodami doświadczalnymi, reprezentacja bazująca na wokselach jest typowym sposobem opisu budowy wewnętrznej materiału. Dla metod wykorzystujących koncepcję przekrojów seryjnych oraz metod tomograficznych, woksele stanowią najmniejsze elementy strukturalne zawierające informacje o analizowanym materiale i w toku analizy, na ich podstawie, dokonywana jest segmentacja (zob. p. 2.3.3) pozwalająca na zrekonstruowanie kształtu niejednorodności. Woksele stosowane są również w metodach symulacyjnych: metodzie Monte Carlo czy automatach komórkowych. Na podstawie analizy stanu tych elementów, dokonywane są specyficzne operacje, pozwalające na odtworzenie syntetycznej mikrostruktury rozpatrywanego tworzywa.
Zapis informacji o budowie wewnętrznej materiału wykorzystujący woksele, jest więc powszechnie stosowany przy tworzeniu DMR. Podejście to pozwala z jednej strony na efektywną analizę podstawowych parametrów mikrostruktury rekonstruowanego materiału, a z drugiej, na późniejsze, bezpośrednie wykorzystanie modeli geometrycznych w symulacjach numerycznych, w których poprzez homogenizację uzyskiwane są właściwości efektywne [774, 902, 986, 1111].
Przeprowadzenie pełnej analizy parametrów mikrostruktury, wymaga jednak dokładniejszego opisu kształtu elementów składających się na model geometryczny. Dotyczy to przede wszystkim analizy parametrów powierzchniowych i liniowych (pola powierzchni międzyziarnowych czy międzyfazowych, krzywizny powierzchni oraz długości i krzywizny krawędzi) [713, 1115]. Również szczegółowa analiza zachowania materiału poddawanego różnorodnym obciążeniom, uwzględniająca lokalizację zjawisk prowadzących przykładowo do inicjacji pęknięć, interakcji między elementami mikrostruktury czy oddziaływania materiału z czynnikami zewnętrznymi (np. analiza przepływu w przypadku materiałów porowatych, transport ciepła, itp.), wymaga bardziej realistycznego przybliżenia kształtu powierzchni elementów modelu geometrycznego. W takich zagadnieniach stosowane jest zwykle drugie podejście, oparte na powierzchniowych siatkach wielokątów. Opis taki uzyskiwany jest poprzez przekształcenie modeli bazujących na wokselach (interpolację połączoną z wygładzaniem powierzchni) albo bezpośrednio, dzięki zastosowaniu podczas segmentacji parametrycznego opisu geometrii [679, 774, 902, 1111, 1114, 1116]. Siatka wielokątów jest również podstawową reprezentacją geometryczną dla metod teselacyjnych, które z natury, opierają się jedynie na opisie elementów powierzchniowych rekonstruowanych niejednorodności. Zastosowanie metod teselacyjnych, pozwala zatem na uniknięcie błędów interpolacyjnych, związanych z przekształcaniem opisu opartego na wokselach w opis oparty na siatkach wielokątów [776, 1117]. Niezależnie jednak od techniki, którą ostatecznie uzyskiwany jest model geometryczny, podejście wykorzystujące powierzchniowe siatki wielokątów, może prowadzić do generowania obiektów o ostrokrawędzistych kształtach albo znikomo małych rozmiarach [1111]. Obecność takich artefaktów może zostać ograniczona już na etapie tworzenia modelu geometrycznego, poprzez wprowadzenie dodatkowych reguł: co do minimalnej, dozwolonej długości elementów liniowych oraz minimalnej wartości kątów między elementami powierzchniowymi. Reguły te, wykorzystywane są niekiedy, także na etapie przetwarzania końcowego, w którym uzyskany model geometryczny poddawany jest regularyzacji [776, 900]. W efekcie, uzyskana siatka powierzchniowa, lepiej oddaje fizyczne zależności dotyczące cech morfologicznych odtwarzanych niejednorodności.
Mając na uwadze zasadniczy cel, dla którego przygotowywane są modele geometryczne, na tym etapie pracy nad DMR, należy uwzględnić również założenia dotyczące rozmiaru rekonstruowanej przestrzeni. Stosując do rekonstrukcji dane uzyskane metodami doświadczalnymi, rozmiar RVE ustalany jest zazwyczaj już na etapie planowania eksperymentu, natomiast w przypadku metod symulacyjnych oraz geometrycznych, rozmiar syntetycznych mikrostruktur dobierany jest na podstawie opisanych już wcześniej kryteriów SVE. Dodatkowo, w trakcie generowania modeli syntetycznych, może zostać wymuszona periodyczność modelu geometrycznego. W najczęściej stosowanych modelach, w których rozpatrywana przestrzeń ograniczona jest sześcianem, periodyczna mikrostruktura realizowana jest przez powtórzenie układu elementów punktowych i liniowych rozmieszczonych na przeciwległych ścianach modelu. W przypadku modeli o nieregularnych kształtach brzegów, periodyczność osiągana jest poprzez powtórzenie odpowiadających sobie płaszczyzn, leżących po przeciwnych stronach modelu i należących do dopełniających się wzajemnie ziaren 60. Wprowadzenie na tym etapie periodycznej geometrii modelu, pozwala na bezpośrednie zastosowanie periodycznych warunków brzegowych w ostatnim etapie pracy nad DMR.
Po uzyskaniu modelu geometrycznego spełniającego przyjęte założenia, w kolejnym etapie pracy nad cyfrową reprezentacją materiału, model taki zostaje uzupełniony informacjami o właściwościach faz składowych. Zastosowany w tym etapie sposób opisu właściwości (implementacja numeryczna) oraz ich zakres, wynika rozpatrywanego zjawiska i metod stosowanych w symulacjach numerycznych (wykorzystywanych solwerów). Niekiedy opis taki uzupełniany jest również o dodatkowe szczegóły, dotyczące właściwości pseudo-faz, wprowadzanych do modelu w celu zastąpienia skomplikowanych, rzeczywistych interakcji występujących w materiale poddawanym zewnętrznym obciążeniom, opisem uproszczonym. Może to dotyczyć przykładowo: częściowego ujednorodnienia właściwości dla wybranych faz w materiałach wielofazowych [178, 339], albo wprowadzenia strefy kohezyjnej (CZM) umożliwiającej symulacje pękania (zob. p. 1.3.5).
Kolejnym istotnym elementem, który musi zostać uwzględniony w toku prac nad DMR, jest orientacja krystalograficzna krystalitów. W przypadku rekonstrukcji opierających się na danych doświadczalnych, odpowiednie informacje są zwykle zbierane w trakcie pomiarów (np. metodą EBSD) i mogą zostać bezpośrednio wykorzystane w modelu geometrycznym. Jeśli jednak dane takie są niedostępne – nie zostały zarejestrowane w pomiarach bądź konstruowany jest nieistniejący jeszcze, syntetyczny materiał, to orientacja osi krystalograficznych dobierana jest najczęściej na podstawie zakładanego rozkładu statystycznego. W przypadku materiałów ceramicznych (jonowo-kowalencyjnych), w których nie stosuje się obróbki poprzez kucie czy walcowanie, pokrój krystalitów obecnych w litym materiale, skorelowany jest z kierunkami krystalograficznymi. Wzajemne ułożenie powierzchni ograniczających rekonstruowane krystality, może więc stanowić wskazówkę, pozwalającą na ustalenie dodatkowych więzi między morfologią ziarna a kierunkiem osi krystalograficznych. Podejście takie sprawdza się szczególnie w przypadku materiałów zawierających wydłużone krystality, w których jedna z osi krystalograficznych pokrywa się z kierunkiem rozrostu ziarna [25, 178, 273, 338].
Ostatni etap pracy nad DMR jest już specyficzny dla metody numerycznej stosowanej w symulacjach. W tym etapie, do modelu obliczeniowego wprowadzane są warunki brzegowe, obciążenia oraz dla metod wykorzystujących siatki (np. MES/FEM), przeprowadzana jest dyskretyzacja. Jeśli do opisu modelu geometrycznego zastosowane zostało podejście oparte na wokselach, to mogą one zostać przekształcone wprost, na siatkę elementów skończonych – siatkę strukturalną [673, 931, 1111, 1116]. Takie rozwiązanie pozwala na proste, automatyczne generowanie modeli obliczeniowych o wysokiej jakości siatki, bezpośrednio na podstawie modeli geometrycznych (rys. 3.6a). Pozwala to dodatkowo uniknąć błędów interpolacyjnych, pojawiających się przy konwersji opisu niejednorodności (przekształcenie siatki wokseli w siatkę powierzchniową).
Podejście to jest jednak nieefektywne obliczeniowo. Równomierna siatka wokseli, która uzyskiwana jest w trakcie rekonstrukcji realizowanej metodami doświadczalnymi czy symulacyjnymi, przekształcona bezpośrednio w siatkę strukturalną, wprowadza nadmierne zagęszczenie elementów w obszarach, w których gradient rozwiązania i tym samym błąd numeryczny, jest niewielki (np. w centrum ziarna). Z kolei w granicach miedzy niejednorodnościami, gdzie występują nagłe zmiany właściwości, rozmiar elementów utworzonych na wokselach może być zbyt duży do osiągnięcia zakładanej dokładności obliczeń [673, 683, 773, 1118]. Aby poprawić efektywność obliczeń, można przeprowadzić ponowną dyskretyzację modelu (ang. remeshing), powodującą lokalną zmiana gęstości siatki. W takim przypadku, wybrane grupy elementów, dla których gradient rozwiązania jest niewielki, zastępowane są pojedynczymi elementami o większych rozmiarach, natomiast w obszarach sąsiadujących z granicami międzyziarnowymi, elementy są dzielone i w ten sposób siatka jest zagęszczana [913, 1119].

Zazwyczaj jednak, w symulacjach wykorzystujących MES/FEM, stosowane są siatki niestrukturalne [931, 1111]. W ostatnich latach opracowanych zostało wiele różnych procedur, pozwalających na uzyskanie takiej siatki na podstawie modelu geometrycznego opartego na wokselach [772, 774, 913, 986, 1005, 1114, 1120–1123]. Procedury te wymagają jednak wstępnej identyfikacji granic między elementami mikrostruktury [772, 1111, 1112, 1114, 1120]. Natomiast w przypadku reprezentacji bazującej na powierzchniowych siatkach wielokątów, zastosowanie siatki niestrukturalnej jest typowym podejściem wykorzystywanym przy tworzeniu modelu obliczeniowego [771, 773, 829, 986, 987, 1114, 1124]. Dla porównania, na rysunku 3.6 przedstawione zostały syntetyczne mikrostruktury poddane dyskretyzacji przy pomocy siatki strukturalnej i niestrukturalnej. Należy zauważyć, że przy odpowiednim doborze rozmiaru elementów, obydwa rodzaje siatek pozwalają na uzyskanie zbliżonych wyników symulacji prowadzonych dla wielu zjawisk. Każde z przedstawionych rozwiązań, jest więc równoważne i posiada zalety, które mogą być decydujące przy ostatecznym wyborze metody dyskretyzacji. Siatki strukturalne, oprócz prostej implementacji w kodzie obliczeniowym, pozwalają również na bezpośrednie zastosowanie periodycznych warunków brzegowych (dla periodycznego modelu geometrycznego), z kolei siatki niestrukturalne, lepiej opisują powierzchnie elementów mikrostruktury i umożliwiają dokładniejsze odwzorowanie skomplikowanych kształtów niejednorodności.
Przedstawione w tym podrozdziale kolejne kroki, służące do uzyskania cyfrowej reprezentacji materiału, ilustrują złożoność zagadnień, które muszą zostać uwzględnione podczas przygotowania modelu numerycznego. Duża specyfika rozwiązań stosowanych na różnych etapach pracy nad DMR, może paradoksalnie, znacząco utrudnić, a w praktyce wręcz uniemożliwić, wymianę danych (opisu geometrii i właściwości materiałowych) pomiędzy alternatywnymi podejściami obliczeniowymi. Intensywny rozwój oprogramowania wspomagającego poszczególne etapy pracy nad wirtualnymi materiałami, coraz częściej udostępnianego przez społeczność naukową na wolnych licencjach 61, wymaga zatem uporządkowania i standaryzacji opisu DMR. Pozwoli to na ściślejszą integrację narzędzi programistycznych i szersze wykorzystanie ich w obliczeniowej inżynierii materiałowej.
Przykład takiej periodycznej mikrostruktury zostanie przedstawiony w kolejnym rozdziale (zob. p. 4.3.4).↩︎
Warto wymienić kilka przykładów
takiego oprogramowania, udostępnianego przez społeczność na wolnych
licencjach, służącego np. do analizy obrazu: ImageJ [1125], rekonstrukcji
mikrostruktury: Neper [1126], generowania siatek: Gmsh
[1127], symulacji
mikromechanicznych: OOF [1128], wizualizacji danych:
ParaView [1129].↩︎
Obserwowana w ostatnich latach, stopniowa zmiana podejścia stosowanego podczas projektowania nowych materiałów oraz optymalizacji właściwości istniejących już tworzyw, związana jest z upowszechnieniem technik obliczeniowych. Techniki te, obejmują coraz szerszy zakres zjawisk bezpośrednio interesujących inżynierów materiałowych. W prowadzonych pracach badawczo-rozwojowych, z powodzeniem wykorzystywane są więc symulacje numeryczne, będące istotnym uzupełnieniem badań doświadczalnych. Równocześnie, rozwój samych metod pomiarowych, wymaga coraz większego zaangażowania technik komputerowych do przetwarzania, wizualizacji i analizy rejestrowanych danych doświadczalnych. Ponoszone przy tym koszty, sprawiają, że ośrodki posiadające zaawansowaną aparaturę pomiarową, wielokrotnie przetwarzają, analizują, ale również udostępniają społeczności naukowo-badawczej, ogromną ilość wysokiej jakości danych. W ostatnich latach pojęcie big data i związana z nim specjalność nazywana informatyką materiałową, stają się coraz częściej wymienianymi terminami w kontekście możliwych kierunków dalszego rozwoju inżynierii materiałowej [757, 1036, 1130]. Obok narzędzi pozwalających na badania doświadczalne, metod numerycznych wykorzystywanych w symulacjach, trzecią grupę, stanowią więc metody służące do analizy uzyskiwanych danych materiałowych. Te trzy komponenty są podstawą, wspomnianego już wcześniej, zintegrowanego podejścia w obliczeniowej inżynierii materiałowej (ICME) [1036, 1131–1133], którego przykładem jest chociażby inicjatywa mająca na celu stworzenie ,,genomu materiałowego” [1134, 1135]. Aby w pełni zrealizować koncepcję ICME, niezbędna jest jednak pełna integracja tych trzech elementów.
Paradygmat dotyczący związku między budową wewnętrzną a właściwościami materiału, ustalony w zeszłym stuleciu jedynie na podstawie obserwacji i analizy wyników pomiarów uzyskiwanych metodami doświadczalnymi, ulega stopniowemu rozszerzeniu [913, 989, 1036]. Stało się jasne, że wyniki takie nie wystarczą do sformułowania pełnego opisu dla wielu istotnych zjawisk. Przykładem, w odniesieniu do materiałów ceramicznych, może być zjawisko kruchego pękania. Analiza wyników doświadczalnych prowadzona przez wiele dziesięcioleci dla różnych materiałów ceramicznych, pozwoliła na fenomenologiczny opis i ustalenie ogólnych zależności rządzących tym zjawiskiem. Zapoczątkowanie procesu pękania jest jednak zawsze zależne od lokalnej konfiguracji pola naprężeń, która wynika z kształtu i rozmieszczenia niejednorodności w materiale. Dlatego pełny opis, musi uwzględniać stochastyczną naturę inicjacji i propagacji pęknięć. Do skonstruowania ilościowych związków dla tego typu zjawisk, wymagana jest więc obszerna baza informacji, które z powodów praktycznych nie mogą zostać zgromadzone jedynie z wykorzystaniem narzędzi doświadczalnych. Dane takie muszą być uzupełniane i rozszerzane danymi uzyskiwanymi poprzez symulacje numeryczne. Tylko w taki sposób możliwe jest uwzględnienie złożoności interakcji zachodzących w rzeczywistych materiałach i uzyskanie precyzyjnego ilościowego opisu.
Gromadzenie, przetwarzanie i analiza danych zarówno doświadczalnych jak i symulacyjnych, wymaga więc ustalenia standardów, które pozwolą na efektywną wymianę informacji między poszczególnymi etapami procesu projektowania i optymalizacji właściwości oraz technik wytwarzania materiału. Relacje między tymi dwoma komponentami ICME (narzędziami doświadczalnymi oraz symulacyjnymi) są oczywiście dwustronne. Informacje uzyskane w pomiarach prowadzonych na rzeczywistym materiale mogą zostać wykorzystywane do uzupełnienia i weryfikacji danych symulacyjnych. Dotyczy to zarówno parametrów opisujących budowę, właściwości podstawowe faz oraz właściwości makroskopowe tworzywa. Z drugiej strony, wyniki symulacji powinny stanowić podstawę do optymalizacji właściwości materiału przez modyfikacje jego mikrostruktury bądź składu. W tym zakresie, potrzebne są zatem funkcje korelacyjne, pozwalające na skuteczne i precyzyjne porównywanie geometrii modelu (syntetycznej mikrostruktury) z budową wewnętrzną rzeczywistego materiału.
Trzecim głównym komponentem ICME są narzędzia informatyczne: programistyczne i bazodanowe, pozwalające na przechowywanie, przetwarzanie, automatyczne analizowanie i udostępnianie zgromadzonych danych materiałowych. Narzędzia te są aktualnie rozwijane w wielu centrach naukowo-badawczych, a przykładowe zostały wymienione już wcześniej w podrozdziale 3.3.2 (zob. tab. [3.1]). Zgodnie z koncepcją ICME, centra te, zajmują się więc przechowywaniem rozległych zbiorów informacji o materiałach, ich ciągłą weryfikacją i uzupełnianiem, ale wiele z nich udostępnia również narzędzia służące do ich przetwarzania [1133]. Dane takie można pobierać za pośrednictwem interfejsów programistycznych (API, ang. Application Programming Interface), co umożliwia ich zautomatyzowane przetwarzanie i ponowne wykorzystywanie.
W ostatnich latach do analizy zgromadzonych danych wykorzystywane są systemy oparte na sztucznej inteligencji (np. komputerowym widzeniu czy maszynowym uczeniu) [757, 1044, 1136, 1137]. Ich zastosowanie dotyczy zarówno systematycznego wyszukiwania wzorców w danych doświadczalnych, które wykorzystywane są następnie do generowania syntetycznych mikrostruktur [601, 757, 1138, 1139], wyznaczania właściwości podstawowych na podstawie danych symulacyjnych uzyskanych metodami ab initio (potencjałów międzyatomowych, struktur krystalicznych, diagramów fazowych) [314, 1140], jak i w inżynierii odwrotnej, w której do zadanych właściwości dobierany jest materiał, albo jego konkretna forma (mikrostruktura), mogąca spełnić zakładane wymagania [1044, 1137]. Wyszukiwanie i ustalanie relacji między budową wewnętrzną a właściwościami tworzyw w oparciu o rozległe zbiory danych (big data), stanowi więc rozszerzenie dotychczasowego podejścia stosowanego w inżynierii materiałowej. Projektowanie w oparciu o dane (ang. data-driven research), w którym istotną rolę odgrywają narzędzia informatyczne pozwalające na integrację wszystkich etapów pracy, ma pozwolić na obniżenie kosztów i przyspieszenie prac badawczo-rozwojowych prowadzonych w celu opracowania nowych materiałów oraz zwiększenia niezawodności komponentów wykorzystywanych aktualnie w przemyśle [1044, 1131].
Najważniejsze elementy zintegrowanego podejścia w obliczeniowej inżynierii materiałowej zostały przedstawione w tabeli [3.2]. Dalszy rozwój tej koncepcji i upowszechnienie projektowania w oparciu o dane, uzależniony jest jednak od tempa w jakim uzupełnione zostaną brakujące powiązania między jej głównymi elementami [913, 1036, 1107]. W odniesieniu do zastosowań przemysłowych, stopniowa zmiana procedur wypracowanych przez lata w zakresie projektowania i doboru materiałów oraz wdrożenie nowych systemów typu CAD/CAM, podobnych do stosowanych już przy projektowaniu strukturalnym, może nastąpić jedynie, gdy osiągnięty zostanie poziom niezawodności, umożliwiający skrócenie czasu wprowadzenia nowej technologii do produkcji, wyraźne obniżenie kosztów projektowania i wytwarzania czy istotne poszerzenie zakresu oferowanych produktów.
W tym rozdziale przedstawione zostały przykłady modeli obliczeniowych opierających się na metodzie elementów skończonych oraz techniki stosowane do ich konstruowania. Modele te były wielokrotnie wykorzystywane w badaniach własnych, dotyczących polikrystalicznych materiałów ceramicznych. Pozwoliły one na analizę właściwości termomechanicznych materiałów węglikowych, tlenkowych i azotkowych oraz ziarnistych kompozytów ceramicznych. Uzyskane na ich podstawie wyniki symulacji mikromechanicznych, były prezentowane i dyskutowane na konferencjach oraz stanowiły główne bądź uzupełniające zagadnienia w opublikowanych pracach badawczych. Ich przybliżenie w tym rozdziale, może więc pozwolić na bliższe zapoznanie się z opisywanymi już wcześniej, wybranymi koncepcjami i rozwiązaniami stosowanymi w obliczeniowej inżynierii materiałowej w odniesieniu do modelowania właściwości materiałów ceramicznych. Niektóre z zaprezentowanych tu rozwiązań, pozwalają na uzyskanie wysokiej dokładności przewidywań dotyczących właściwości termomechanicznych tworzyw ceramicznych. Mogą zatem stanowić podstawę do analiz inżynierskich prowadzonych w zakresie badań materiałowych wspomaganych symulacjami numerycznymi.
Przegląd rozwiązań podzielony jest na dwie zasadnicze części. W pierwszej, zostały opisane modele mikromechaniczne wykorzystujące dwuwymiarową reprezentację mikrostruktury. Niewielkie wymagania obliczeniowe oraz stosunkowo proste techniki pozwalające na szybkie przygotowanie modeli 2D, sprawiają, że mogą one służyć do wstępnej weryfikacji zastosowanych rozwiązań, podczas budowy zaawansowanych modeli 3D. Zastosowanie modeli 2D do analizy właściwości materiałów polikrystalicznych jest jednak ograniczone. Uproszczenia dotyczące geometrii powodują, że dla wielu zjawisk, uzyskiwane wyniki symulacji mogą być podstawą jedynie do badań jakościowych. Pomimo tego modele 2D z powodzeniem mogą być stosowane w analizach porównawczych, pozwalających rozpoznanie mechanizmów odpowiedzialnych za umocnienie czy wpływających na wytrzymałość tworzyw ceramicznych. Analizy takie, stanowią więc użyteczne rozszerzenie badań doświadczalnych, uzupełniające zasób informacji o badanym materiale i pozwalające dodatkowo na wizualizację rozpatrywanych zagadnień.
Część druga tego rozdziału zawiera opis modeli wykorzystujących trójwymiarowe odwzorowanie budowy wewnętrznej materiałów. Na przykładzie zrealizowanych prac własnych, przedstawione zostały kolejne kroki pozwalające na uzyskanie syntetycznych mikrostruktur 3D dla jedno- i wielofazowych materiałów polikrystalicznych. W tej części została również zilustrowana, wspomniana wcześniej (zob. p. 3.4.2), procedura pozwalająca na oszacowanie rozmiaru SVE. Warto również zaznaczyć, że przygotowanie przedstawionych tutaj modeli 3D, wymaga znacznie większego nakładu pracy, ale uzyskiwane na ich podstawie wyniki symulacji, wykazują bardzo dobrą zgodność z wynikami pomiarów doświadczalnych.
Modele mikromechaniczne opierające się na dwuwymiarowym opisie mikrostruktury (modelach geometrycznych 2D) są najmniej wymagające, jeśli chodzi o zasoby obliczeniowe. Ewentualne poprawki czy zamierzone, systematyczne zmiany geometrii, mogą być łatwo wprowadzane do modelu. Pozwala to na szybkie, automatyczne generowanie dużej liczby realizacji, co może mieć znaczenie przy optymalizacji mikrostruktury bądź analizie porównawczej, prowadzonej dla rozpatrywanego tworzywa. Z uwagi na niewielkie wymagania sprzętowe (stosunkowo małą liczbę elementów niezbędnych do dyskretyzacji modelu), modele 2D są również często wybierane przy rozpatrywaniu zjawisk silnie nieliniowych (np. zjawiska pękania), dla których niezbędne jest wielokrotne powtarzanie obliczeń, aż do osiągnięcia zakładanego kryterium numerycznego, co znacząco wydłuża czas potrzebny do osiągnięcia zbieżności rozwiązania.
Dwuwymiarowy model geometryczny, reprezentujący mikrostrukturę rozpatrywanego materiału, może zostać przygotowany w programach typu CAD. W najprostszym przypadku, do odwzorowania budowy wewnętrznej może posłużyć nawet odręczny szkic, wykonany na podstawie zarejestrowanego obrazu mikrostruktury (rys. 4.1a-b). Takie podejście jest jednak podatne na szereg błędów i przy wymaganej większej precyzji odwzorowania oraz rozmiarze modelu jest bardzo czasochłonne. Bardziej efektywny sposób, pozwalający na przekształcenie obrazu mikrostruktury w model geometryczny, opiera się na obrazach binarnych (rys. 4.1c-d). Obrazy takie, uzyskiwane w trakcie analizy mikrostruktury, są zapisywane w postaci plików rastrowych (bitmap, zob. p. 2.3), a zatem muszą zostać poddane konwersji do formy wektorowej, umożliwiającej parametryczny opis geometrii. Przekształcenie to można przeprowadzić przy pomocy narzędzi do wektoryzacji (programów do trasowania). Jakość konwersji zależy jednak od rozdzielczości pliku binarnego i uzyskany w ten sposób opis geometrii wymaga niekiedy ręcznej korekty.
W pracach nad mechanizmami związanymi z oddziaływaniem między ziarnami, przydatne są również modele o uproszczonej geometrii, w których kształty niejednorodności można wyrazić przy pomocy niewielkiej liczby parametrów. W takim przypadku opis opiera się na prostych figurach geometrycznych (ang. geometric primitives), z których budowane są bardziej złożone kształty, reprezentujące analizowany układ modelowy 4.1e. Prowadząc rekonstrukcję mikrostruktury metodami symulacyjnymi albo geometrycznymi, wykorzystywany w nich sposób parametrycznego opisu wirtualnego materiału zależy od zastosowanej techniki i narzędzia, ale zwykle ewentualna konwersja do wymaganego formatu wektorowego nie jest skomplikowana.
W przypadku symulacji mikromechanicznych mających na celu analizę lokalnych oddziaływań między niejednorodnościami, istotne jest ograniczenie wpływu granic modelu geometrycznego na rozkład pola rozpatrywanego parametru. Relaksacja albo spiętrzenie wartości w obszarach przylegających do granic modelu, które wynikają z niedostatecznego albo nadmiernego podparcia, powodują zaburzenie rozkładu analizowanego pola, co może utrudnić lub nawet uniemożliwić właściwą interpretację uzyskiwanych wyników. Jest to szczególnie niekorzystne, gdy rozmiar modelu geometrycznego jest niewielki (model zawiera małą liczbę elementów mikrostruktury), co zdarza się często dla rekonstrukcji opartych na obrazach mikrostruktury. Aby uniknąć takich efektów można rozszerzyć model geometryczny o dodatkową warstwę otaczającą, która pośredniczyć będzie w przekazywaniu obciążeń, i do której przyłożone będą niezbędne do przeprowadzenia obliczeń podparcia 4.1f.
Dalsze prace związane są już bezpośrednio z przygotowaniem modelu obliczeniowego. Oprócz informacji o geometrii, niezbędny jest więc wybór modeli materiałowych (równań konstytutywnych) oraz wprowadzenie do nich wymaganych parametrów opisujących właściwości. Modele takie muszą zostać przypisane do wszystkich elementów składowych modelu obliczeniowego. W przypadku symulacji dotyczących właściwości termosprężystych, prowadzonych dla materiałów ceramicznych, najczęściej wykorzystywanym modelem materiałowym jest model liniowo-sprężysty. Ponieważ zmiany wartości stałych materiałowych (np. stałych sprężystości, współczynników rozszerzalności cieplnej) wraz ze zmianą temperatury są nieznaczne, to w przypadku uproszczonych modeli 2D wykorzystywane są zwykle wartości stałe tych parametrów. Takie uproszczenie może być jednak przyjęte tylko dla analiz prowadzonych w ograniczonym zakresie temperatury – dla właściwości termosprężystych do temperatury \(T_{\text{sf}}\) (temperatury relaksacji naprężeń, zob. p. 1.4).
Kolejne założenia wynikają wprost z dwuwymiarowej geometrii modelu. Sprowadzając zachowanie rzeczywistego materiału do jego dwuwymiarowej reprezentacji, należy w modelu obliczeniowym określić, w jaki sposób uproszczony zostanie trzeci, nieobecny w modelu geometrycznym wymiar. W tym celu stosowane jest przybliżenie modelu do warunków płaskiego stanu naprężenia (PSN) lub odkształcenia (PSO). Niekiedy wprowadzany jest dodatkowy wymiar, uzyskiwany poprzez ,,wyciągnięcie” modelu geometrycznego w kierunku prostopadłym do jego płaszczyzny (zwykle jest to kierunek \(z\)) i wtedy symulacje prowadzone są dla modelu pseudo-3D. W przypadku materiałów polikrystalicznych i kompozytów ziarnistych, często wybierany jest PSN (model traktowany jest jak cienka płyta, \(\sigma_z = 0\)). Należy jednak zaznaczyć, że niezależnie od przyjętych założeń, dwuwymiarowe modele pozwalają na uzyskanie jedynie przybliżonych rozkładów naprężenia oraz odkształcenia, co utrudnia ich ilościowe porównanie z wartościami wyznaczonymi doświadczalnie.
Kolejnym elementem modelu obliczeniowego, opisanym już przy omawianiu DMR, jest orientacja układu odniesienia. Zwykle główny (globalny) układ odniesienia jest określony przy pomocy prostokątnego układu współrzędnych, zorientowanego tak, że jego płaszczyzna \(xy\) pokrywa się z płaszczyzną modelu geometrycznego. Aby uwzględnić różne orientacje osi krystalograficznych krystalitów, z każdą częścią modelu obliczeniowego, reprezentującą kolejne krystality albo wtrącenia, wiązany jest lokalny układ współrzędnych (LCS). Zmiana orientacji LCS względem głównego układu odniesienia, pozwala więc na zróżnicowanie kierunków krystalograficznych w modelowanym polikrysztale czy kompozycie (rys. 4.2b). Orientacje LCS ustalane są w oparciu o dane doświadczalne lub symulacyjne. W przypadku niedostępności takich danych, wartości kątów rotacji LCS względem głównego układu odniesienia, dobierane są tak, aby uzyskać zakładany, statystyczny rozkład orientacji krystalitów [338, 541]. Przybliżone orientacje osi LCS mogą zostać również przyjęte w oparciu o charakterystyczne cechy morfologiczne (wydłużenie, spłaszczenie), które mogą być związane ze strukturą krystaliczną ziaren [25, 178, 338]. Gdy model konstruowany jest na podstawie obrazów mikrostruktury, pomocne mogą być także obserwacje kształtu i ułożenia tarasów krystalicznych. Ujawniają się one niekiedy na powierzchni próbki wskutek trawienia termicznego lub chemicznego, wykorzystywanego do uwidocznienia pozycji granic międzyziarnowych [25] (rys. 4.2a).

W zależności od stosowanych do obliczeń solwerów, przy zmianie orientacji LCS, konieczne może być wyznaczenie skorygowanych wartości parametrów opisujących właściwości materiałowe dla poszczególnych, różnie ułożonych w przestrzeni, części modelu (np. wartości modułów sprężystości czy współczynników rozszerzalności cieplnej). Niezależnie jednak od wykorzystywanych do przeprowadzenia symulacji pakietów obliczeniowych, etap związany z wprowadzeniem do modelu informacji o właściwościach materiału jest kluczowy. Ewentualne błędy w skryptach kodujących dane dla solwera oraz w samych wartościach stałych materiałowych wprowadzanych do modelu, mogą być trudne do późniejszego wykrycia, dlatego na tym etapie model powinien zostać poddany wnikliwiej weryfikacji. Często w tym celu, przeprowadzane są symulacje testowe dla uproszczonej geometrii, których wyniki porównane są z wartościami wyznaczonymi metodami analitycznymi.
Dla kompozytów ziarnistych, w których kształt wtrąceń jest izometryczny, oraz gdy dodatkowo anizotropia właściwości termomechanicznych jest niewielka, w uproszczonych modelach 2D można założyć izotropię faz składowych. Takie uproszczenie powoduje, że nie jest potrzebne przypisywanie LCS do poszczególnych ziaren. Wprowadzane do takiego modelu parametry materiałowe faz, mogą zostać przyjęte zarówno na podstawie danych uzyskanych z pomiarów doświadczalnych, odpowiadających uśrednionym właściwościom makroskopowym, jak również mogą zostać wyznaczone przy pomocy analitycznych metod homogenizacyjnych. Przybliżenie takie może być także niezbędne, gdy szczegółowe wartości parametrów materiałowych są niedostępne (np. brakuje danych dotyczących wartości współczynników macierzy sztywności, a dostępne są jedynie wartości średnie odpowiednich modułów sprężystości) albo identyfikacja faz składowych jest niepełna, co często dotyczy faz amorficznych lokujących się w przestrzeni międzyziarnowej. Pomimo tak daleko idących uproszczeń w opisie właściwości faz składowych, modele takie nadal pozwalają na prowadzenie użytecznych analiz jakościowych. Przykładowo, przeprowadzone porównanie rozkładu wartości naprężeń resztkowych dla kompozytów \(\text{SiC-TiB}_{\text{2}}\), wyznaczonych przy zastosowaniu anizotropowych i izotropowych właściwości fazy węglikowej oraz borkowej, wskazuje [338], że uzyskane rozkłady różnią się szerokością (rozrzutem wartości naprężenia) oraz wartościami średnimi, jednak jakościowo, wyniki symulacji są ze sobą w pełni zgodne (rys. 4.3).
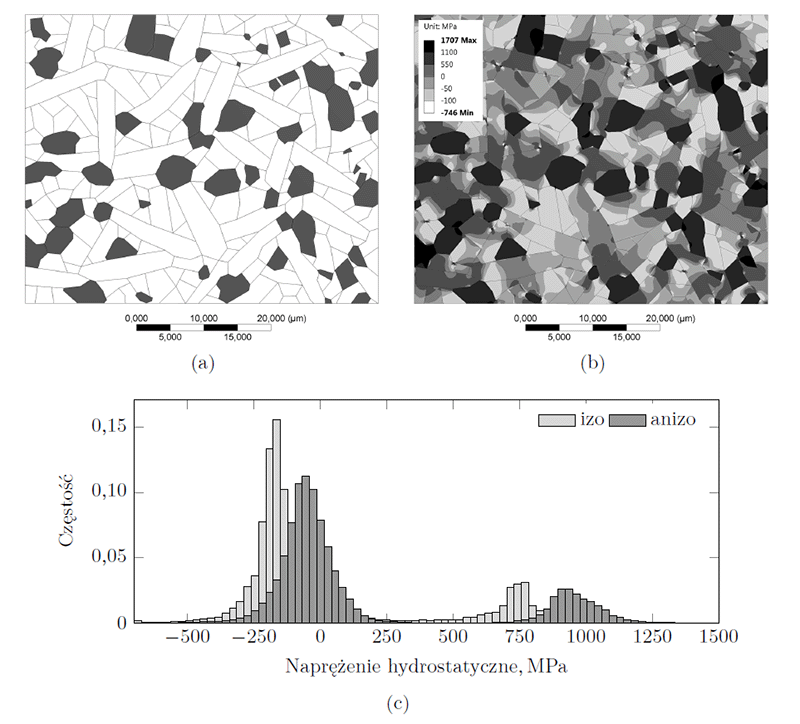
Podczas prac związanych z przygotowaniem modeli obliczeniowych, muszą również zostać ustalone podparcia i narzucone obciążenia. Rodzaj zastosowanych podparć oraz przyjęte w symulacjach obciążenia, są specyficzne dla rozpatrywanego zjawiska i założonych warunków brzegowych. Także na tym etapie model powinien zostać poddany wnikliwej weryfikacji w celu wyeliminowania ewentualnych błędów mogących wynikać z nadmiernego bądź niedostatecznego umocowania modelu czy sposobu wymuszenia obciążeń.
Ostatnim krokiem przed rozpoczęciem właściwych obliczeń jest dyskretyzacja modelu. Jest to kolejny, kluczowy dla uzyskiwanych później wartości, etap prac modelowych. Siatka elementów skończonych musi zostać przygotowana w formacie specyficznym dla wykorzystywanego w obliczeniach solwera. Dostępnych jest wiele specjalistycznych narzędzi (generatorów siatek), które mogą zostać wykorzystane w celu uzyskania wysokiej jakości siatki. Etap ten wymaga jednak szczególnej uwagi, ponieważ od jakości siatki zależy nie tylko czas w jakim osiągnięta będzie zbieżność rozwiązania (ukończone zostaną obliczenia), ale i dokładność wyników symulacji.
Aby uzyskać optymalne zagęszczenie siatki, w modelach MES opartych na mikrostrukturze, przyjmuje się, że najmniejszy rozmiar elementów (największe zagęszczenie) powinien występować w obszarach opisujących granice międzyziarnowe. Z kolei centrum ziaren, gdzie gradienty rozwiązania są niewielkie, siatka może zostać rozrzedzona. Takie podejście pozwala istotnie zredukować rozmiar modelu, a później także plików zawierających wyniki symulacji, przy zachowaniu dużej dokładności numerycznej rozwiązania (rys. 4.4).

Rozmiar elementów zastosowanych do dyskretyzacji przy zakładanym, dopuszczalnym błędzie numerycznym, zależy od geometrii modelu: kształtu krystalitów, ziaren czy innych niejednorodności; właściwości materiałowych: stopnia anizotropii, zróżnicowania właściwości między fazami (niedopasowania termomechanicznego), ale również od zastosowanych podparć i przyjętych obciążeń (analizowanego zjawiska). Dlatego siatka poddawana jest w toku pracy optymalizacji. Zazwyczaj, wychodząc od roboczo określonych parametrów siatki, opisujących jej rozmiar i zmienność w obrębie dyskretyzowanych części modelu, prowadzi się kilka symulacji wstępnych, w których parametry te są stopniowo modyfikowane – zmienia się lokalne zagęszczenie elementów, zgodnie z przyjętą procedurą optymalizacji. Następnie, porównując wyniki takich symulacji, ustalane są docelowe parametry siatki, zapewniające kompromis pomiędzy dokładnością uzyskiwanych wyników i czasem niezbędnym na przeprowadzenie właściwych obliczeń. W celu przyspieszenia tego etapu, optymalizację siatki można przeprowadzić na modelu geometrycznym o zredukowanych rozmiarach, a ustalone w ten sposób parametry zastosować następnie do pełnowymiarowego modelu czy zespołu realizacji.
Z uwagi na stosowane przybliżenia geometryczne i materiałowe, wykorzystanie modeli 2D dla wielu zjawisk ogranicza się do analiz jakościowych i porównawczych. Przykładem takich zastosowań mogą być prace własne, dotyczące mechanizmów odpowiedzialnych za umocnienie, obserwowane w kompozytach ziarnistych \(\text{SiC-AlN}\) oraz \(\text{SiC-TiB}_{\text{2}}\) [170, 200, 201]. Dwuwymiarowe modele obliczeniowe, zostały w tych pracach przygotowane zarówno na podstawie uproszczonych modeli geometrycznych, składających się ze szczeliny umieszczonej między ziarnami wtrąceń, jak i na podstawie obrazów rzeczywistej mikrostruktury tych kompozytów (rys. 4.5a-b). Przeprowadzone symulacje zachowania materiału poddawanego jednoosiowemu rozciąganiu, ujawniły zasadnicze różnice występujące między badanymi kompozytami w rozkładzie pola naprężenia w pobliżu wierzchołka szczeliny (rys. 4.5c-d). Różnice te, zostały powiązane z niedopasowaniem termomechanicznym faz składowych kompozytów, co pozwoliło na tłumaczenie, obserwowanych dla analizowanych materiałów rozbieżności w odchylaniu pęknięć propagujących przez osnowę w pobliżu ziaren fazy wtrąconej. W połączeniu z wynikami badań doświadczalnych, przeprowadzone symulacje numeryczne, umożliwiły więc wskazanie przyczyn większego umocnienia, obserwowanego dla kompozytu o osnowie węglikowej w porównaniu z kompozytem azotkowym.
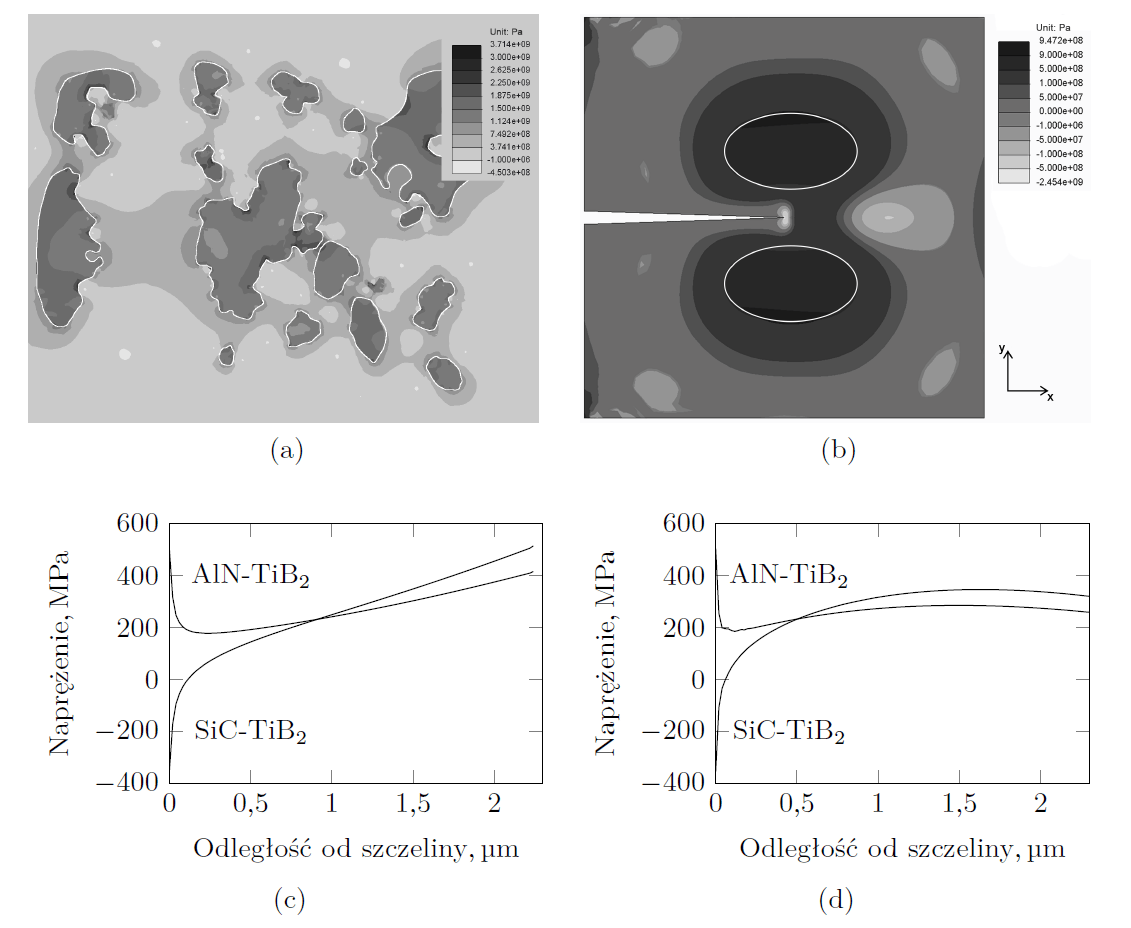
Podobne podejście zostało również zastosowane do analizy odporności na pękanie dla ceramicznych kompozytów ziarnistych: \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\text{-WC}\) i \(\text{TZP-WC}\) oraz kompozytów o ceramicznej osnowie i metalicznych wtrąceniach: \(\text{Al}_{\text{2}}\text{O}_{\text{3}}\text{-W}\) i \(\text{TZP-W}\) [261]. W pracy tej, opartej na wynikach badań doświadczalnych i symulacjach numerycznych prowadzonych dla uproszczonych modeli geometrycznych, także wykazane zostały istotne różnice w rozkładzie naprężenia. Występowały one w pobliżu wierzchołka pęknięcia i były wywołane obecnością wtrąceń, niejednakowo modyfikujących pole naprężenia występujące w rozpatrywanych układach. Obserwacja ta, w połączeniu z analizą fraktograficzną, pozwoliła na potwierdzenie roli granic międzyziarnowych w mechanizmie pękania. Złożony stan naprężenia występujący w badanych kompozytach w obszarach przylegających do powierzchni wtrąceń, mógł zarówno aktywować pękanie w granicach między wtrąceniami a osnową, jak i uruchamiać bardziej efektywny dla tego typu materiałów mechanizm, prowadzący do odchylania pęknięć w samej osnowie.
Wyniki symulacji przeprowadzonych w wymienionych pracach, wskazywały dodatkowo, że istotną składową naprężenia obecnego w polikrystalicznych materiałach ceramicznych, jest składowa pochodząca od resztkowych naprężeń cieplnych. Możliwość kumulacji RTS w tego typu tworzywach może zatem decydować o sposobie pękania materiału poddawanego zewnętrznym obciążeniom i przez to wpływać na odporność na pękanie oraz wytrzymałość. Obserwacje te, stały się podstawą do szeregu prac modelowych, w których analizie poddany został wpływ niedopasowania termomechanicznego, kształtu ziaren oraz udziału objętościowego wtrąceń na rozkład RTS w kompozytach ziarnistych.
Przykładem takich prac może być analiza wpływu kształtu wtrąceń na kierunek propagacji pęknięć, przeprowadzona dla kompozytów \(\text{ZrO}_{\text{2}}\text{-Al}_{\text{2}}\text{O}_{\text{3}}\) [186]. Badania, w których wykorzystane były dwuwymiarowe modele geometryczne oparte na uproszczonej modelowej mikrostrukturze i założone w nich izotropowe właściwości faz, pozwoliły na ustalenie jakościowych zależności między krzywizną wtrąceń a rozkładem RTS. Zauważono, że dla rozpatrywanego układu, w pobliżu cząstek wypukłych o niskiej wartości współczynnika kształtu \(1/f_c\) (izometrycznym kształcie i niewielkim pofałdowaniu powierzchni, zob. p. 2.2.2), rozkład naprężenia w osnowie jest jednorodny, natomiast dla cząstek o silnym rozwinięciu powierzchni, pojawia się duże zróżnicowanie rozkładu naprężenia. Dotyczyło to głównie składowej rozciągającej naprężenia, przez co mogło wpływać na propagację pęknięcia i, dla cząstek wydłużonych o złożonym kształcie, sprzyjało pękaniu wskrośziarnowemu. Pomimo jakościowego charakteru przeprowadzonych symulacji, uzyskane na ich podstawie wyniki, mogą stanowić wskazówkę przy projektowaniu i optymalizacji właściwości tego typu tworzyw, prowadzonych poprzez modyfikację mikrostruktury na etapie przygotowania wyjściowych proszków stosowanych do spiekania.
Bardziej złożone, dwuwymiarowe modele geometryczne, zostały zastosowane w przypadku analizy rozkładu resztkowych naprężeń cieplnych w polikrystalicznych kompozytach ceramicznych z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)–\(\text{ZrO}_{\text{2}}\)–\(\text{WC}\), zawierających fazy ciągłe [18]. Duży udział objętościowy składników takich kompozytów, przekraczający znacznie punkt perkolacji, sprawia, że fazy składowe wzajemnie przenikają się tworząc struktury, których szczegółowy opis wymaga uwzględnienia złożonych zależności topologicznych i morfologicznych. W pracy, do zrekonstruowania budowy wewnętrznej tych materiałów w sposób uproszczony, zastosowany został parametryczny model geometryczny 2D, który pozwolił na uwzględnienie jedynie udziału objętościowego składników oraz długości granic międzyfazowych (rys. 4.6a).

W modelach obliczeniowych przyjęte zostały izotropowe właściwości składników analizowanych kompozytów i dla układu potrójnego, uzyskane w przeprowadzonych symulacjach, maksymalne wartości RTS sięgały 2 GPa. Głównymi czynnikami, które wpływały na tak duże wartości wyznaczonych naprężeń resztkowych, były różnice w rozszerzalności cieplnej i wzajemne ułożenie faz. Przeprowadzone dodatkowo, porównawcze symulacje RTS dla modelu 2D, wykorzystującego obrazy rzeczywistej mikrostruktury rozpatrywanych tworzyw, wskazały jednak, że uproszczony model parametryczny nie pozwala na zaawansowaną analizę interakcji między elementami składowymi w tego typu kompozytach. Ograniczenie to wynika przede wszystkim ze zbyt dużych uproszczeń, przyjętych co do kształtu granic międzyfazowych i ich wzajemnego rozmieszczenia. W tym zakresie, dwuwymiarowe modele oparte na obrazach mikrostruktury zapewniają lepsze odwzorowanie skomplikowanych zależności występujących w kompozytach ziarnistych i pozwalają na precyzyjniejszą identyfikację czynników odpowiedzialnych za kumulację RTS.
Modele takie, wykorzystujące obrazy rzeczywistej mikrostruktury, zostały zastosowane w pracach własnych dotyczących wielu układów kompozytowych. Przykładami mogą tu być badania prowadzone dla kompozytów ziarnistych: \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\text{-WC}\), \(\text{Al}_{\text{2}}\text{O}_{\text{3}}\text{-ZrO}_{\text{2}}\) [367], \(\text{SiC-TiB}_{\text{2}}\) [455], \(\text{TiC-Cr}_{\text{3}}\text{C}_{\text{2}}\) [28], kompozytów z układu \(\text{ZrO}_{\text{2}}\)–\(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) zawierających nanometryczne wtrącenia \(\text{TiC}\) [370, 372, 373] czy dla układu \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\)–\(\gamma\text{-AlON}\) [1142]. Zastosowane w tych pracach modele geometryczne, zostały przygotowane na podstawie obrazów binarnych, wykorzystywanych podczas ilościowej analizy mikrostruktury, stanowiącej wcześniejszy etap badań. Podejście to pozwoliło na precyzyjne odwzorowanie mikrostruktury i uwzględnienie w modelach obliczeniowych dużej liczby elementów budowy wewnętrznej o zróżnicowanym kształcie i rozmiarze. W modelach tych stosowana była dodatkowa warstwa otaczająca, której właściwości termomechaniczne odpowiadały właściwościom osnowy lub były wyznaczone na podstawie homogenizacji właściwości faz składowych przeprowadzonej metodami analitycznymi (zob. p. 3.2).
Uzyskane w tych pracach wyniki symulacji numerycznych, konfrontowane były z obserwacjami mikroskopowymi, badaniami fraktograficznymi oraz wynikami pomiarów odporności na pękanie i wytrzymałości. Tego typu hybrydowe podejście (doświadczalno-symulacyjne), pozwalało poszerzyć zbiór informacji, na podstawie których, ostatecznie analizowane były właściwości kompozytów. W efekcie ułatwiało to weryfikację hipotez dotyczących mechanizmów umocnienia czy wpływu mikrostruktury na odporność na pękanie i wytrzymałość badanych tworzyw.
Warto jednak zaznaczyć, że pomimo znacznych uproszczeń geometryczno-materiałowych, dwuwymiarowe modele numeryczne wykorzystujące syntetyczne bądź zrekonstruowane mikrostruktury, pozwalają na wyznaczanie wartości średnich wybranych parametrów, zbliżonych do wartości obliczonych na podstawie równań analitycznych (w przypadku RTS, często stosowanych równań Selsinga [408] czy Taya i in. [415], zob. p. 1.4.4). Co prawda, rozbieżność wartości może być zbyt duża, aby modele te mogły stanowić podstawę do ilościowej analizy właściwości materiału, ale w zakresie niepewności pomiarowej, pozwalają na analizę interakcji między niejednorodnościami oraz na lokalizację elementów budowy, istotnie wpływających właściwości tworzyw. Potwierdza to przydatność tego typu modeli w badaniach podstawowych oraz przy optymalizacji mikrostruktury tworzyw ceramicznych, prowadzonej w celu poprawy lub modyfikacji ich właściwości makroskopowych.
Główne kroki i techniki stosowane przy pracy nad trójwymiarowymi modelami obliczeniowymi są podobne do tych, które były opisane dla modeli 2D. Zasadnicze różnice dotyczą modeli materiałowych, a w szczególności parametrów wymaganych do ich opisu, oraz etapu przygotowania modeli geometrycznych (3D). Znacząco wzrastają również wymagania sprzętowe, wydłuża się czas symulacji i zwiększa rozmiar danych, które muszą zostać przetworzone w trakcie obliczeń, a później zapisane w postaci plików wynikowych.
W symulacjach dotyczących zagadnień termosprężystych dla polikrystalicznych materiałów ceramicznych, podobnie jak w przypadku modeli 2D, najczęściej wykorzystywany do opisu właściwości materiałowych jest model liniowo-sprężysty. Jednak z uwagi na brak ograniczeń geometrycznych, stosowany jest tutaj opis właściwości odnoszący się do trzech wymiarów. Dla właściwości sprężystych, może więc zostać uwzględniona pełna anizotropia krystalitów albo przy wyższej ich symetrii ortotropia (liczba niezbędnych współczynników macierzy sztywności czy podatności sprężystej, zależy od symetrii rozpatrywanych krystalitów). Właściwości opisywane tensorami niższego rzędu (np. przewodnictwo cieplne czy rozszerzalność cieplna), wymagają określenia trzech – a dla wyższej symetrii dwóch lub jednego – niezależnych współczynników głównych, wyrażających wartości w kierunku osi przyjętego układu współrzędnych. Podobnie jak w przypadku modeli 2D, w zależności od stosowanego solwera, wymagana może być transformacja macierzy opisujących właściwości (korekcja wartości współczynników materiałowych), zgodna z orientacją lokalnych układów odniesienia (LCS), przypisanych do poszczególnych części modelu geometrycznego. Dla faz amorficznych, albo gdy niedostępne są szczegółowe parametry materiałowe (współczynniki sztywności czy rozszerzalności cieplnej), stosowany jest izotropowy opis właściwości termosprężystych.
Aby zwiększyć dokładność symulacji dla procesów zachodzących przy zmianie temperatury (np. symulacji RTS), parametry materiałowe opisywane są zależnościami funkcyjnymi (względem temperatury) albo wprowadzane w postaci tabelarycznej dla wybranych przedziałów temperatury. Gdy symulacje prowadzone dla polikrystalicznych materiałów ceramicznych, dotyczą zjawisk zachodzących w temperaturze przekraczającej temperaturę relaksacji naprężeń (\(T_{\text{sf}}\)), niezbędne jest rozszerzenie opisu modelu materiałowego uwzględniające zachowanie sprężysto-plastyczne albo sprężysto-lepkoplastyczne.
W przeciwieństwie do prostych modeli geometrycznych stosowanych w symulacjach 2D, odwzorowanie mikrostruktury w trzech wymiarach wymaga wykorzystania opisu parametrycznego. Nie jest więc możliwe odtworzenie budowy wewnętrznej na podstawie odręcznego szkicu czy na podstawie prostego przekształcenia dwuwymiarowych obrazów bezpośrednio w model 3D.
Jedna z podstawowych technik, która może być wykorzystana do utworzenia trójwymiarowego modelu mikrostruktury materiału kompozytowego, oparta jest na reprezentacji ziaren w postaci prostych brył geometrycznych. Do przybliżenia kształtu wtrąceń stosowane są: wielościany (czternastościan Kelvina, sześcian, osiemnastościan, dwudziestościan, itp.), graniastosłupy (o podstawie heksagonalnej, pentagonalnej, kwadratowej), walce, elipsoidy, a niekiedy kule (rys. 4.7a). W tego typu podejściu zakłada się, że osnowa, czy faza międzyziarnowa, jest jednorodna – to znaczy, nie posiada własnej struktury polikrystalicznej. Przyjęcie takiego założenia jest w pełni uprawnione dla faz amorficznych. Stosowane jest ono również, gdy rozmiar krystalitów osnowy jest dużo mniejszy niż rozmiar wtrąceń (szczególnie w przypadku krystalitów posiadających symetrię regularną, kiedy pomijalna jest anizotropia rozpatrywanych właściwości) albo dla fazy, której właściwości materiałowe przyjmowane są w modelu jako izotropowe.

Podczas konstruowania syntetycznych modeli geometrycznych kompozytów, gdy niedostępne są szczegółowe dane doświadczalne dotyczące rozmiaru ziaren, ich rozmieszczenia i orientacji względnej, cechy te dla poszczególnych brył reprezentujących ziarna, dobierane są na podstawie zakładanego (teoretycznego) rozkładu statystycznego. Stosowana jest w tym celu metoda MC i generatory liczb pseudolosowych. Proste kształty, wykorzystywanych w tym podejściu brył geometrycznych, pozwalają również na powiązanie orientacji lokalnych układów odniesienia z ułożeniem ich charakterystycznych osi symetrii.
Proces generowania syntetycznej mikrostruktury, realizowany jest automatycznie poprzez skrypty sterujące. W zadeklarowanej przestrzeni, najczęściej ograniczonej sześcianem, rozmieszczane są kolejno wybrane bryły. Na tym etapie może zostać wymuszona również periodyzacja mikrostruktury. Część bryły, która nie zawiera się w zakładanej przestrzeni modelu, zostaje ,,odcięta” i przesunięta na przeciwległą ścianę modelu geometrycznego (rys. 4.7). Przy większym udziale objętościowym wtrąceń (większym wypełnieniu powierzchni bryłami), często dochodzi do wzajemnego nakładania się generowanych figur. W zależności od przyjętego podejścia rekonstrukcyjnego, wymagane może być więc dodatkowe sprawdzanie warunku nakładania, w celu ewentualnego wyeliminowania takiego zdarzenia. Wykorzystanie tego warunku na etapie rozmieszczania brył, pozwala na uzyskanie mikrostruktury zawierającej izolowane wtrącenia, jednak podejście to znacząco wydłuża czas niezbędny na uzyskanie zakładanego udziału objętościowego. Staje się to szczególnie widoczne przy większych wartościach wypełnienia i w praktyce ogranicza możliwość uzyskania mikrostruktury zawierającej ponad 50 % obj. wtrąceń. Wartość ta zależy jednak od kształtu oraz zakładanego zróżnicowania rozmiaru brył i dla silnie wydłużonych graniastosłupów czy elipsoid, może być niższa, a dla brył o izometrycznym kształcie i zróżnicowanym rozmiarze, wyższa (rys. 4.7b).
Pomimo tych ograniczeń, technika wykorzystująca proste bryły geometryczne jest użyteczna szczególnie w przypadku konstruowania modeli służących do symulacji, stanowiących uzupełnienie badań doświadczalnych. Uproszczona geometria pozwala na badanie głównych czynników wpływających na właściwości rozpatrywanego materiału, co w połączeniu z analizą danych doświadczalnych ułatwia weryfikację hipotez badawczych [339]. Technika ta jest również przydatna do rekonstrukcji budowy wewnętrznej materiałów, dla których pomiary parametrów mikrostrukturalnych są obarczone dużym błędem. Taka niepewność pomiarowa może wynikać z niewielkiego kontrastu fazowego utrudniającego segmentację (np. z powodu obecności fazy amorficznej w obszarach międzyziarnowych), czy z dużego zróżnicowania rozmiaru krystalitów poszczególnych faz, przekraczającego rozdzielczość stosowanej metody badawczej [178]. Przyjęcie, w takim przypadku, daleko idących przybliżeń geometrycznych, co do kształtu elementów mikrostruktury, nie wpływa istotnie na i tak niewielką precyzję opisu budowy wewnętrznej, a pozwala na przeprowadzenie szeregu symulacji mogących ułatwić zrozumienie głównych zależności występujących między mikrostrukturą a właściwościami analizowanego tworzywa. Możliwość odtworzenia syntetycznej mikrostruktury na podstawie niewielkiej liczby parametrów, jest zatem główną zaletą tej techniki. W praktyce, do budowy trójwymiarowego modelu geometrycznego wystarczają podstawowe informacje ilościowe o udziale objętościowym faz oraz wyniki jakościowe, pozwalające na dobranie brył, które najlepiej przybliżać będą kształt wtrąceń obecnych w badanym materiale.
Szczegółowy model geometryczny, wymagany w symulacjach, których celem jest uzyskanie ilościowego opisu zachowania materiału, musi uwzględniać rzeczywisty kształt niejednorodności, ich rozmieszczenie, orientację oraz zmienność tych cech – musi spełniać założenia RVE. Aby uzyskać taki model, niezbędna jest znajomość szeregu parametrów mikrostruktury, które w przypadku rekonstrukcji budowy rzeczywistego materiału, muszą zostać pozyskane metodami doświadczalnymi. Najpełniejszy zestaw informacji o materiale, pod względem ilości i jakości danych, można uzyskać metodami tomograficznymi i metodami opierającymi się na koncepcji przekrojów seryjnych (zob. rozdz. 2.5). Specyfika budowy wewnętrznej polikrystalicznych materiałów ceramicznych (np. niewielki rozmiar krystalitów, duża twardość, mały kontrast fazowy) sprawia, że wykorzystanie tych metod w badaniach materiałowych prowadzonych dla tej grupy tworzyw, jest nadal ograniczone. Wynika to głównie z niewielkiej dostępności aparatury pozwalającej na osiągnięcie wymaganej precyzji obrazowania, czasochłonności pomiarów i w efekcie dużych kosztów jednostkowych ponoszonych podczas badań. Alternatywą mogą być więc pomiary przeprowadzone klasycznymi technikami stereologicznymi.
Przykładem prac własnych, w których do trójwymiarowej rekonstrukcji mikrostruktury wykorzystane zostały dane uzyskane na podstawie analizy zgładów metalograficznych, są badania dotyczące polikrystalicznego tlenku glinu, tlenku cyrkonu i ich kompozytów ziarnistych [540, 541, 771]. W toku tych prac, przeprowadzona została analiza obrazu (której kroki były już omawiane wcześniej, zob. rozdz. 2.3 i rys. 2.6), a uzyskane obrazy binarne posłużyły do analizy mikrostruktury. W ten sposób, wyznaczone zostały rozmiary cząstek zarejestrowanych na obrazach (powierzchnie, obwody, średnice Fereta, średnice równoważne 2D) i współczynniki kształtu oraz wydłużenia, a dla kompozytów, dodatkowo udział objętościowy faz (zob. rozdz. 2.2). Z uwagi na niewielkie odstępstwo kształtu obserwowanych cząstek od kolistości – na co wskazywały wartości współczynników kształtu, wydłużenia i różnice między średnicami Fereta – przyjęto, że pokrój krystalitów budujących te materiały jest izometryczny. Założenie to pozwoliło na wykorzystanie metody Scheila–Schwartza–Sałtykowa (SSS, zob. rozdz. 2.2.5) do transformacji rozkładów średnic równoważnych cząstek (2D) do rozkładów średnic równoważnych dla krystalitów (3D). Przejście to jest kluczowe podczas prac nad trójwymiarową rekonstrukcją mikrostruktury i pozwala na statystyczne odwzorowanie w modelu, zróżnicowania rozmiaru krystalitów występującego w rzeczywistym materiale (rys. 4.8a).
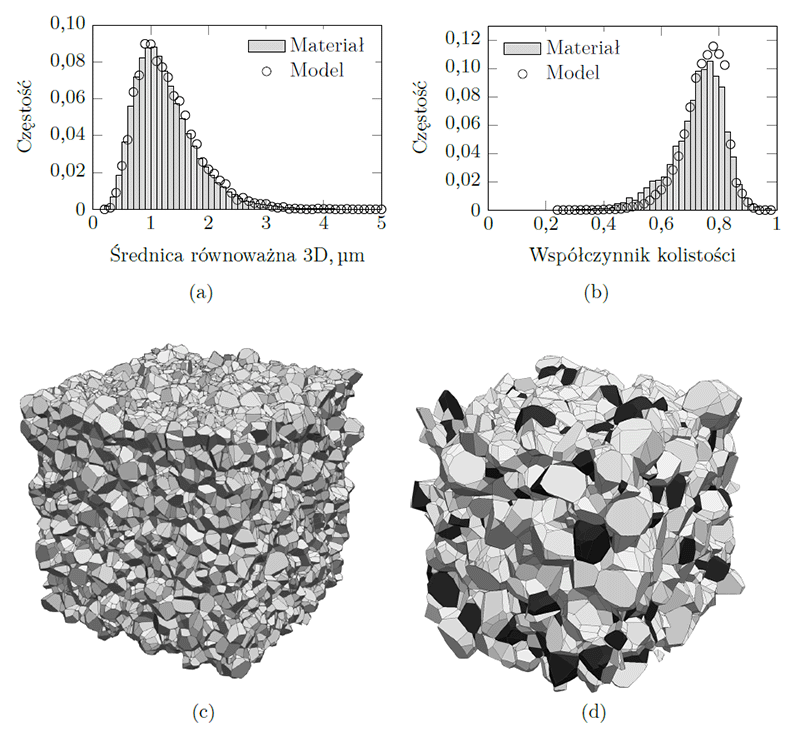
Trójwymiarowe rekonstrukcje mikrostruktury polikryształów i kompozytów ziarnistych z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)–\(\text{TZP}\), zostały w tych pracach uzyskane metodą teselacji Laguerre’a (zob. p. 2.6.4.2). Do optymalizacji geometrii wykorzystane zostały rozkłady średnic równoważnych 3D i współczynnika kolistości. Pozwoliło to na uzyskanie modeli geometrycznych, w których rozmiar i kształt komórek teselacyjnych był statystycznie równoważny rozmiarom i kształtom krystalitów w rzeczywistych polikryształach (rys. 4.8). Takie podejście rekonstrukcyjne, umożliwiło więc opis budowy rzeczywistych materiałów, ale może być również zastosowane w przypadku badań projektowych, gdy opracowywane jest nowe tworzywo czy optymalizowana jest mikrostruktura materiału i niedostępne są jeszcze, niezbędne do budowy modelu geometrycznego, dane doświadczalne.
W przypadku symulacji mających na celu analizę lokalnych zjawisk decydujących o makroskopowym zachowaniu materiału, szczególnie dla prostych modeli 2D, reprezentatywność modelu geometrycznego ma drugorzędne znaczenie. Rozmiar przestrzeni i wynikająca z niego możliwość uwzględnienia pełnej reprezentacji wszystkich elementów mikrostruktury, nie jest parametrem krytycznym dla uzyskiwanych wyników i oczekiwanej odpowiedzi modelu numerycznego na postawione pytania badawcze. Zazwyczaj rozmiar modelu i pozycja okna mikrostrukturalnego, dobierane są arbitralnie, tak aby rozpatrywany obszar zawierał interesujące, często wręcz nietypowe, konfiguracje ziaren i elementy mikrostruktury. Przykładowo, tego typu podejście jest stosowane przy konstruowaniu modeli obliczeniowych mających służyć do analizy mechanizmów umocnienia, gdy uproszczenia modelu geometrycznego i istotnie ograniczona reprezentacja niejednorodności, pomaga w wyekstrahowaniu podstawowych czynników odpowiedzialnych za rozpatrywane zjawisko [168, 170, 201, 261, 268, 501]. Również w modelach 2D, których geometria została odwzorowana bezpośrednio na podstawie obrazów mikrostruktury, czynnik związany z subiektywnym doborem obserwowanego, a później zapisanego w postaci cyfrowego obrazu, obszaru próbki, może nie pozwalać na spełnienie warunku losowego doboru próby i tym samym utrudniać uzyskanie reprezentatywności [28, 201, 367, 370, 454, 455].
Jednak w symulacjach prowadzonych na trójwymiarowych modelach obliczeniowych, których celem jest zapewnienie ilościowego opisu analizowanych zjawisk, reprezentatywność ma pierwszorzędne znaczenie. Ponieważ rozmiar reprezentatywnego – albo częściej – statystycznie reprezentatywnego elementu objętościowego, jest uzależniony nie tylko od cech mikrostrukturalnych, ale również od właściwości materiału i rodzaju rozpatrywanego zjawiska (zob. rozdz. 3.4), to rozmiar ten określany jest zazwyczaj a posteriori, na podstawie analizy uzyskiwanych wyników symulacji.
W badaniach własnych, zagadnienie to było szczegółowo analizowane w pracy dotyczącej modelowania rozszerzalności cieplnej polikryształów \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\), \(\text{TZP}\) oraz kompozytów ziarnistych z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)–\(\text{TZP}\) [771]. Opracowana technika szacowania rozmiaru SVE, której podstawy teoretyczne zostały opisane już w punkcie 3.4.2, była również wykorzystana w badaniach nad wpływem resztkowych naprężeń cieplnych na właściwości polikrystalicznego \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) i jego kompozytów: \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) oraz \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\) [178]. Zastosowana w tych pracach technika, jest niezależna od metod rekonstrukcyjnych wykorzystywanych do uzyskania modelu geometrycznego. Na jej podstawie można wyznaczyć rozmiar SVE zarówno dla modeli dwu- jak i trójwymiarowych. Wymaga ona stosunkowo niewielkiego nakładu pracy, niezbędnego do uzyskania informacji o liczebności zespołu realizacji, zapewniającej osiągnięcie wyników symulacji mieszczących się w zakresie zakładanego, dopuszczalnego błędu obliczeniowego.
W przeprowadzonych badaniach polikryształów \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\), \(\text{TZP}\) i ich kompozytów [771], w celu ustalenia docelowej liczebności SVE (\(n_{\text{SVE}}\)), oparto się na wynikach uzyskanych z pięciu pilotażowych realizacji. Aby jednak zebrać wystarczająco dużą liczbę danych porównawczych, w pracy tej analizowane były jednocześnie wyniki dla rekonstrukcji o objętości od 1 μm3 do 8000 μm3, zawierających, w zależności od materiału i charakterystycznego dla niego średniego rozmiaru krystalitów, od kilkunastu do prawie 4 tysięcy ziaren. Zestawienie objętości \(V_{\text{SVE}}\) i odpowiadających im liczebności ziaren \(n_g\), dla rozpatrywanych materiałów, zawarte zostało w tabeli [4.1].
Zebrany w trakcie badań, duży zestaw danych, pozwolił na systematyczną analizę błędów wyznaczenia właściwości pozornej (w pracy [771] oparto się na rozszerzalności cieplnej) dla kolejnych rozmiarów rekonstruowanych mikrostruktur i poszczególnych materiałów (tab. [4.1]). Zgodnie z przypuszczeniami, największy rozrzut wartości właściwości pozornej i tym samym błąd względny \(\delta_{\text{abs}}^{\text{app}}\), występował dla rekonstrukcji o najmniejszych rozmiarach \(V_{\text{SVE}}\) i liczebności ziaren \(n_g\). W przypadku takich rekonstrukcji, uzyskanie wyników odpowiadających właściwości efektywnej przy zakładanym poziomie ufności (95 %), wymagało przeprowadzenia symulacji dla najbardziej licznych zespołów realizacji (dla kompozytu AZ35 przy objętości 1 μm3, która zawierała zaledwie 17 ziaren, wymagane były aż 152 realizacje). Jednak dla rekonstrukcji zawierających po kilkaset ziaren, rozrzut uzyskiwanych wartości pozornych istotnie malał, co obniżało wymagania odnośnie liczebności zespołu realizacji. Dla takich rekonstrukcji statystycznie reprezentatywny zespół składał się z kilkunastu realizacji.
Z przeprowadzonej w pracy [771] analizy wynika, że w badaniach dotyczących właściwości termomechanicznych rozpatrywanych materiałów polikrystalicznych, uzyskanie statystycznie reprezentatywnej objętości jest możliwe przy stosunkowo niewielkich rozmiarach modeli geometrycznych i liczebności zespołów realizacji. Spostrzeżenie to może być użyteczne nie tylko w kontekście symulacji numerycznych, ale również pracach doświadczalnych, w których istotne jest ograniczenie rozmiaru analizowanej przestrzeni i liczebności badanych próbek.
Warto również zwrócić uwagę na specyfikę rekonstrukcji dla materiałów kompozytowych. Niewielka liczba krystalitów zawarta w realizacjach o najmniejszych objętościach, może nie zapewnić wystarczającego zróżnicowania rozmiaru, kształtu i orientacji wtrąceń. Efekt ten jest szczególnie widoczny w przypadku kompozytów ziarnistych o najmniejszym udziale objętościowym fazy wtrąconej i powoduje duży rozrzut właściwości pozornych uzyskiwanych w kolejnych symulacjach. Dlatego w tego typu materiałach, celowe jest zwiększenie całkowitej liczebności ziaren w rekonstrukcjach, tak aby liczebność wtrąceń przekraczała przynajmniej wartość kilkunastu ziaren. Takie podejście pozwala na istotne zmniejszenie liczby realizacji, wymaganej do uzyskania zakładanego poziomu błędu wyznaczenia właściwości efektywnej.
Wnioski te zostały potwierdzone również we wspomnianej już pracy dotyczącej \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) i kompozytów: \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) oraz \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\) [178]. Przedstawiona technika szacowania rozmiaru SVE, pozwoliła na przygotowanie zestawu realizacji, które umożliwiły na efektywne przeprowadzenie symulacji resztkowych naprężeń cieplnych w badanych materiałach azotkowych.
Sposób w jaki ograniczone zostaną stopnie swobody modelu (wprowadzone będą więzy, podparcia) oraz przenoszone będą na model zakładane obciążenia, decyduje o możliwości poprawnego i efektywnego rozwiązania problemu obliczeniowego przy pomocy MES oraz metod pokrewnych. Jak już wspomniano wcześniej, dobór warunków brzegowych, a w szczególności implementacja odpowiadających im równań w kodzie obliczeniowym, zależy od rodzaju analizowanego zagadnienia i wykorzystywanego w symulacjach solwera. W przypadku symulacji mikromechanicznych, opierających się na modelach geometrycznych odwzorowujących budowę mikrostrukturalną materiału, często stosowane są periodyczne warunki brzegowe (PBC). Zapewniają one stosunkowo szybkie osiągnięcie zbieżności (ukończenie obliczeń) i pozwalają na ograniczenie niepożądanego wpływu zaburzeń (relaksacji bądź spiętrzenia wartości rozwiązania), mogących pojawić się w obszarach zewnętrznych, na wartości rozwiązania uzyskiwane we wnętrzu modelu (zob. p. 3.4.1). Pomimo dobrze zdefiniowanych teoretycznych podstaw PBC, ich implementacja nie jest trywialna i istotnie wpływa na sposób dyskretyzacji modelu. Jednym z warunków, które powinny zostać spełnione, aby można było bezpośrednio wykorzystać PBC, jest periodyczna mikrostruktura, a właściwie jej odwzorowanie w postaci modelu geometrycznego. Nie jest to warunek konieczny 62, ale istotnie upraszcza implementację PBC i pozwala na uniknięcie błędów wynikających z nieperiodycznej siatki elementów na brzegach modelu.
W przypadku rekonstrukcji mikrostruktury dokonywanej metodami doświadczalnymi (tomograficznymi lub na podstawie przekrojów seryjnych), uzyskiwane modele geometryczne, które są dokładnym odwzorowaniem budowy wewnętrznej polikryształów, nie są periodyczne. Stosuje się wtedy techniki pozwalające na wprowadzenie quasi-periodycznych warunków brzegowych albo przyjmowane są inne rodzaje warunków brzegowych (KUBC, SUBC, zob. p. 3.4.2). Dla modeli geometrycznych otrzymywanych metodami symulacyjnymi lub geometrycznymi, periodyczność można wymusić już na etapie generowania wirtualnej mikrostruktury. Uzyskiwane w ten sposób periodyczne modele geometryczne polikryształów, mogą przyjmować precyzyjnie określony, zewnętrzny kształt rekonstruowanej przestrzeni (zwykle jest to sześcian lub prostopadłościan), albo mogą dopuszczać nieregularność powierzchni, wynikającą z obecności na niej ,,nieprzyciętych” do zakładanych wymiarów modelu geometrycznego ziaren (zob. rys. 4.8). Obydwa sposoby reprezentacji rekonstruowanej mikrostruktury są równoważne, jednak regularny, płaski kształt powierzchni ograniczających model, upraszcza nieco dalsze kroki niezbędne do przygotowania modelu obliczeniowego (dyskretyzację i narzucenie więzów). Z drugiej strony, przycinanie ziaren, może prowadzić do pojawienia się na powierzchni modelu, małych ostrokrawędzistych elementów, pozostałych po odcięciu reszty ziarna, co może generować błędy podczas dyskretyzacji [771].
Przykładem prac własnych, w których wykorzystane zostały PBC, mogą być badania nad kompozytami ziarnistymi \(\text{SiC-TiC}\) [339], jednofazowymi polikryształami i kompozytami z układu \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\)–\(\text{TZP}\) [25, 771] oraz polikrystalicznym \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) i jego kompozytami ziarnistymi [178]. Zarówno w pracy [339] jak i [178] zastosowane zostały modele mikrostruktury uzyskane techniką geometryczną (losowe rozmieszczenie prostych brył geometrycznych, zob. rys. 4.7), w których powierzchnie zewnętrzne modelu były płaskie. W kontekście implementacji PBC, ciekawsze mogą być więc prace przeprowadzone dla polikryształów i kompozytów tlenkowych [25, 771], w których rekonstrukcja mikrostruktury zrealizowana została metodą teselacji Laguerre’a i uzyskane modele geometryczne posiadały nieregularne powierzchnie zewnętrzne. W pracach tych, periodyczne warunki brzegowe zostały ustanowione poprzez powiązanie przemieszczeń dla odpowiadających sobie punktów węzłowych, leżących na przeciwległych, periodycznych ścianach modelu. Powiązanie to można przedstawić ogólnym równaniem [771, 1145, 1146]: \[\label{eq:PBCs} u_i^{f^+}\! - u_i^{f^-}\! = \varepsilon_{ij}(x_j^{f^+}\! - x_j^{f^-}),\] w którym indeksy \(i\) oraz \(j\) oznaczają trzy kierunki w głównym układzie odniesienia (\(i, j = 1, 2, 3\)), a różnica przemieszczeń \(u_i^{f^+}\! - u_i^{f^-}\!\), odpowiadających sobie punktów węzłowych leżących na przeciwległych ścianach modelu \(f^+\!\) i \(f^-\!\), związana jest tensorem makroskopowego odkształcenia \(\varepsilon_{ij}\) z różnicą między pozycjami tych węzłów \(x_j^{f^+}\! - x_j^{f^-}\!\). Implementacja tego równania w kodzie obliczeniowym została zrealizowana z wykorzystaniem węzłów sprzęgających (DN, ang. Dummy Nodes). Węzły takie mogą pośredniczyć zarówno w przekazywaniu obciążeń jak i rejestrować wywołaną nimi odpowiedź modelu (rys. 4.9).
W skryptach obliczeniowych zostały zastosowane trzy węzły sprzęgające DN, odpowiadające za połączenie węzłów leżących na periodycznych powierzchniach zewnętrznych, niezależnie dla trzech kierunków głównych w modelu (\(\text{DN}_x\), \(\text{DN}_y\), \(\text{DN}_z\)). Sprzężenie między odpowiednimi węzłami zostało wymuszone przy pomocy równań więzi: \[\label{eq:DN} \begin{split} U\!X_n^{f^+_x} - U\!X_n^{f^-_x} &= U\!X^{\text{DN}_x}\!, \\ UY_n^{f^+_y} - UY_n^{f^-_y} &= UY^{\text{DN}_y}\!, \\ U\!Z_n^{f^+_z} - U\!Z_n^{f^-_z} &= U\!Z^{\text{DN}_z}\!, \end{split}\] w których przykładowo: \(U\!X_n^{f^+_x}\) i \(U\!X_n^{f^-_x}\) oznaczają przemieszczenia rejestrowane w modelu obliczeniowym w kierunku \(x\) dla kolejnych \(n\) par periodycznych węzłów, leżących na powierzchniach ograniczających model w kierunku \(x\), a \(U\!X^{\text{DN}_x}\) oznacza przemieszczenie odpowiedniego węzła sprzęgającego, kontrolującego odkształcenia modelu w tym kierunku.
W przypadku symulacji, w których wykorzystywane są obciążenia mechaniczne (np. dotyczących analizy właściwości sprężystych), węzły sprzęgające mogą służyć zarówno do wymuszenia, jaki do rejestracji odkształcenia modelu. W opisywanych pracach własnych [25, 771], analizowane były jednak zmiany wywołane obciążeniami cieplnymi i węzły te służyły do ograniczenia liczby stopni swobody modelu (jako podparcia) i do rejestracji średnich przemieszczeń zewnętrznych ścian modelu, niezależnie dla trzech głównych kierunków w przyjętym układzie odniesienia.
Przedstawione rozwiązanie, pozwalające na zastosowanie PBC w symulacjach mikromechanicznych, wymaga periodycznej siatki elementów dla przeciwległych powierzchni, leżących na zewnętrznych ścianach modelu. Siatka taka musi zostać wygenerowana na etapie dyskretyzacji modelu. Odpowiadające sobie pary węzłów – periodyczne węzły siatki elementów, które zostaną sprzężone równaniami więzi \eqref{eq:DN}, charakteryzują się identycznymi wartościami współrzędnych położenia w kierunku prostopadłym do kierunku periodyczności. Natomiast wartości współrzędnej określającej położenie węzłów w kierunku równoległym, różnią się o stałą wartość (o wymiar modelu). Z uwagi na potencjalnie bardzo dużą liczbę węzłów, które mogą stanowić periodyczne pary, do ich wyszukania oraz implementacji odpowiednich równań więzi, stosuje się skrypty, które automatyzują ten etap pracy.
Zostały również opracowane techniki pozwalające na wykorzystanie PBC w przypadku nieperiodycznych modeli geometrycznych zob. np. [25, 1055, 1061, 1062, 1102, 1143, 1144].↩︎
Trójwymiarowe modele geometryczne, opisujące rzeczywistą bądź syntetyczną mikrostrukturę materiałów polikrystalicznych, mogą być wykorzystywane zarówno bezpośrednio, w analizach mikrostrukturalnych, jak i służyć do budowy modeli pozwalających na symulacje mikromechaniczne, mające na celu wyznaczenie makroskopowych właściwości tworzyw albo lokalizację istotnych efektów wpływających na te właściwości. Przykładem prac własnych, w których użyte zostały modele 3D, mogą być wymienione już badania, dotyczące kompozytów \(\text{SiC-TiC}\) [339], polikrystalicznego \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\) [540, 541], polikryształów \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) i 3Y-TZP oraz ich kompozytów ziarnistych [771, 1147], czy polikrystalicznego \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) spiekanego z dodatkiem \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) i \(\text{Y}_{\text{2}}\text{O}_{\text{3}}\), oraz jego kompozytów ziarnistych: \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) i \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\) [178, 1097, 1148].
Modele mikrostruktury, które w wymienionych pracach zostały uzyskane metodą geometryczną (przez losowe rozmieszczenie prostych brył geometrycznych) i stosowane były do opisu budowy kompozytów ziarnistych, opierały się jedynie na założeniach pozwalających na odwzorowanie przybliżonego kształtu wtrąceń i udziału objętościowego faz. Należy je więc zaliczyć raczej do modeli opisujących syntetyczne mikrostruktury. Natomiast modele uzyskane na podstawie teselacji Laguerre’a, oparte były na szerszym zestawie danych mikrostrukturalnych i tym samym można je traktować jako modele rekonstrukcyjne. Takie podejście wykorzystane było w pracach dotyczących \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\) [540, 541], w których przeprowadzona została analiza porównawcza danych mikrostrukturalnych uzyskanych dla zrekonstruowanych mikrostruktur z danymi doświadczalnymi. Oprócz rozkładów: rozmiaru krystalitów i współczynnika kształtu, porównane zostały również wartości kątów dwuściennych (rys. 4.10). Wyniki przeprowadzonej w tych pracach analizy statystycznej, potwierdziły dobrą zgodność danych pochodzących z pomiarów przeprowadzonych dla wirtualnej mikrostruktury, uzyskanej poprzez teselację Laguerre’a, z danymi doświadczalnymi. Dodatkowo, opracowana w trakcie prac ścieżka rekonstrukcyjna (opisana już w p. 4.3.4), pozwoliła na budowę modeli polikryształów zawierających bardzo dużą populację krystalitów (kilkadziesiąt tysięcy) przy akceptowalnym koszcie obliczeniowym. Wyniki przeprowadzonych analiz, potwierdziły więc przydatność takich rekonstrukcji w badaniach mikrostrukturalnych oraz wskazywały na możliwość wykorzystania ich w symulacjach mikromechanicznych w roli modeli geometrycznych, które dobrze opisują budowę ceramicznych materiałów polikrystalicznych.
Natomiast uproszczone modele geometryczne, zostały wykorzystane w badaniach kompozytów \(\text{SiC-TiC}\) [339]. Przyjęcie takiego podejścia wynikało z niewielkiego kontrastu fazowego, występującego pomiędzy składnikami analizowanych tworzyw. Z uwagi na zachodzące podczas syntezy reakcje między węglikiem krzemu i tlenkowymi aktywatorami spiekania (10 % wag.), osnowa w uzyskanych materiałach zawierała szereg faz których identyfikacja (XRD) obarczona była dużą niepewnością [339]. Obserwacje mikrostruktury prowadzone przy pomocy SEM, wraz z analizą składu chemicznego EDS, pozwoliły ostatecznie na jednoznaczną segmentację jedynie dla wtrąceń \(\text{TiC}\). Taki podstawowy zestaw informacji o budowie wewnętrznej materiału, narzucił więc dalszy tok postępowania przyjętego podczas opracowania modeli obliczeniowych. Oprócz uproszczonej geometrii (rys. 4.11), w symulacjach, wykorzystane zostały więc izotropowe właściwości faz składowych – osnowy i wtrąceń.

Uzyskane wyniki symulacji resztkowych naprężeń cieplnych, powstających w trakcie procesu syntezy rozpatrywanych tworzyw, analizowane były przede wszystkim jakościowo. Pozwoliło to na ustalenie obecności w osnowie naprężeń ściskających, a we wtrąceniach, rozciągających – w pracy oparto się na wartościach naprężenia hydrostatycznego \(\sigma_h = (\sigma_x + \sigma_y + \sigma_z)/3\). Dodatkowo, przeprowadzone ilościowe analizy porównawcze dla rozkładu RTS w badanych tworzywach, wskazywały na wzrost wartości naprężeń maksymalnych, występujący wraz ze wzrostem udziału objętościowego wtrąceń \(\text{TiC}\). Obserwacje te w połączeniu z wynikami badań doświadczalnych, pozwoliły na potwierdzenie hipotezy dotyczącej istotnej roli RTS w umocnieniu występującym w rozpatrywanych kompozytach. Wyznaczony dla badanych próbek kompozytów wzrost odporności na pękanie, który połączony był z jednoczesnym obniżaniem ich wytrzymałości, był również skorelowany z udziałem objętościowym fazy wtrąconej (\(\text{TiC}\)), a duże wartości RTS wyznaczone w symulacjach, wskazywały na możliwość inicjacji mikrospękań w granicach międzyziarnowych. Połączenie badań doświadczalnych z symulacjami mikromechanicznymi, pozwoliło zatem na powiązanie obserwowanych zależności między składem ilościowym kompozytów, a ich podstawowymi właściwościami mechanicznymi.
Pomiar oraz ilościowa analiza rozkładu resztkowych naprężeń cieplnych były jednym z głównych tematów badawczych, które zostały podjęte w pracy dotyczącej tworzyw na bazie polikrystalicznego \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) [178, 1097]. Wykorzystano w nich zarówno pomiary RTS wykonane metodą dyfrakcji promieniowania rentgenowskiego w geometrii stałego kąta padania (SKP) [354], jak i symulacje mikromechaniczne, oparte na modelach syntetycznej mikrostruktury, statystycznie równoważnej mikrostrukturze rozpatrywanych tworzyw (przykładowy model geometryczny został opisany już wcześniej, zob. rys. 4.7b). Specyfika zastosowanych metod, pozwalała na uzyskanie komplementarnych danych i porównanie stanu naprężenia wewnątrz materiału (MES), ze stanem występującym w jego warstwie powierzchniowej (SKP). Jednak przede wszystkim, wyniki przeprowadzonych badań umożliwiły wykazanie istotne różnic pomiędzy wartościami naprężeń resztkowych obecnych w polikrystalicznym \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) spiekanym z dodatkiem 6 % wag. \(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) i 4 % wag. \(\text{Y}_{\text{2}}\text{O}_{\text{3}}\), a jego kompozytami \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) oraz \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\) zawierającymi 20 % obj. wtrąceń. Różnice te, wynikające z niedopasowania termomechanicznego faz składowych, były przewidywane na podstawie rozważań teoretycznych. Z uwagi na złożoną budowę wewnętrzną tego typu tworzyw – wielofazowych materiałów polikrystalicznych – powszechnie stosowane równania analityczne, nie umożliwiały jednak określenia wartości RTS.
Wyniki przeprowadzonych w pracy [178, 1097] symulacji MES, pozwoliły stwierdzić, że spośród badanych materiałów, najniższe wartości naprężenia obecne są dla bazowego azotku krzemu w silnie wydłużonych ziarnach \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) (\(\sim\)−30 MPa). Natomiast w amorficznej fazie tlenkowej, ulokowanej w przestrzeni międzyziarnowej tego materiału, wartości naprężenia są z kolei największe (\(\sim\)270 MPa). Taki stan naprężenia, wraz z silnie wydłużonym kształtem krystalitów, sprzyjał uruchamianiu mechanizmów podnoszących odporność na kruche pękanie. Wyznaczona w pracy dla tego tworzywa wartość \(K_{\text{Ic}}=\)8.8 ± 0.9 MPa m1/2.
Stan ten zmieniał się jednak w materiałach kompozytowych. Dla kompozytu \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\), obecność dodatkowej fazy, której rozszerzalność cieplna była pośrednia (wartości współczynników \(\alpha\) pomiędzy wartościami dla \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) i fazy tlenkowej), sprawiła, że zmniejszyły się wartości naprężenia wyznaczone dla fazy amorficznej. Niedopasowanie termomechaniczne między krystalitami \(\text{SiC}\) a \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), spowodowało jednak zwiększenie bezwzględnych wartości naprężeń w tych fazach. Obliczone dla \(\text{SiC}\) naprężenie średnie, osiągało wartość \(\sim\)270 MPa, a dla \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), wzrastało do \(\sim\)−70 MPa. Zmiana ta powodowała wyraźne obniżenie odporności na pękanie wyznaczonej doświadczalnie dla tego materiału (\(K_{\text{Ic}}=\)4.6 ± 0.6 MPa m1/2).
Z kolei kompozyt \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) posiadał wtrącenia, których rozszerzalność cieplna była większa, zarówno od dominującej fazy \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), jak i od fazy tlenkowej. Podobnie jak w kompozycie zawierającym ziarna \(\text{SiC}\), powodowało to obniżenie wartości naprężenia w fazie amorficznej (\(\sim\)71 MPa) i wyraźne zwiększenie wartości bezwzględnej naprężenia w ziarnach \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\) (\(\sim\)−440 MPa). Dodatkowo, średnie wartości naprężenia wyznaczone dla ziaren fazy wtrąconej \(\text{TiN}\), osiągały bardzo dużą wartość (\(\sim\)1660 MPa). Taki stan naprężenia sprzyjał wzrostowi odporności na pękanie (\(K_{\text{Ic}}=\)8.9 ± 0.3 MPa m1/2), prawdopodobnie poprzez inicjację mikrospękań w granicach między silnie naprężonymi ziarnami \(\text{TiN}\).
Szczegółowa analiza wpływu naprężeń cieplnych na właściwości mechaniczne tworzyw polikrystalicznych, nie mogła opierać się jednak, wyłącznie na wartościach średnich naprężenia. Przedstawione tutaj wnioski zostały sformułowane w oparciu o pełny zestaw wyników symulacji. Wykorzystane zostały w tym celu histogramy RTS oraz wizualizacje wyników, pozwalające na szczegółową analizę rozkładu naprężenia (przykład na rys. 4.12). Warto tutaj zauważyć, że za makroskopowe właściwości mechaniczne tworzyw polikrystalicznych, mogą być odpowiedzialne zjawiska, których inicjacja zachodzi pod wpływam naprężeń ekstremalnych. Dlatego jakościowa i ilościowa analiza uzyskiwanych wyników symulacji musi uwzględniać również rozrzut uzyskiwanych wartości w czym pomocne mogą być histogramy i mapy rozkładu analizowanych parametrów.
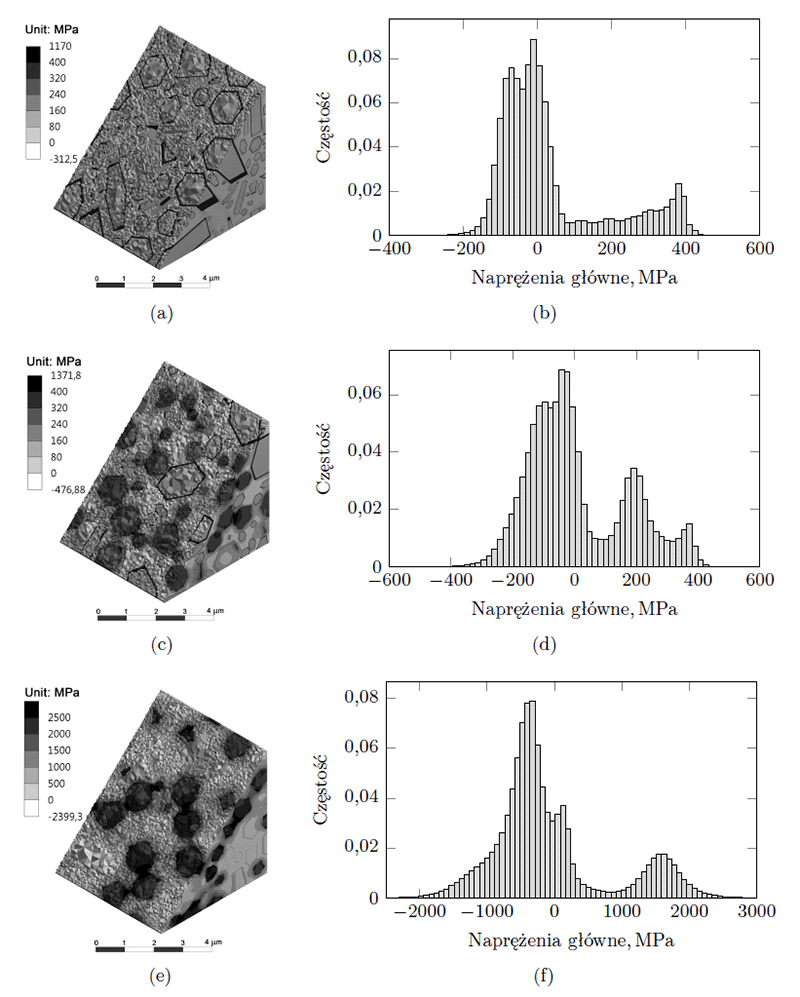
Uzyskane podczas pracy nad tworzywami na bazie azotku krzemu, wyniki pomiarów doświadczalnych, przeprowadzonych metodą dyfrakcji promieniowania rentgenowskiego (SKP), były jakościowo zgodne z wynikami symulacji MES. Specyfika wykorzystanej metody pomiarowej, która wynika z ograniczonej głębokości penetracji materiału przez promieniowanie (zob. p. 1.4.2), powoduje, że uzyskiwane wyniki odnoszą się jedynie do warstwy przypowierzchniowej (w przypadku rozpatrywanych w pracy materiałów i zastosowanego źródła promieniowania, do głębokości 35 μm–45 μm). Przy analizie wyników uzyskanych w tego typu pomiarach, należy mieć więc na uwadze fakt, że wyznaczone wartości RTS odpowiadają stanowi częściowo zrelaksowanemu na skutek możliwości swobodnego odkształcenia próbki w kierunku prostopadłym do jej powierzchni. W połączeniu z wynikami symulacji, daje to możliwość analizy zmian zachodzących w materiale w trakcie pękania. Niestety, na wartości RTS uzyskiwane metodami powierzchniowymi, mają również wpływ efekty wywołane przygotowaniem próbek do pomiarów (cięciem, szlifowaniem itp., zob. p. 1.4.2). Pomimo stosowania technik minimalizujących ten niekorzystny wpływ obróbki powierzchni, nie można oczekiwać, że zostanie on całkowicie wyeliminowany.
Jednak uzyskane w pracy wyniki pomiarów doświadczalnych (SKP), potwierdziły obecność złożonego stanu naprężenia dla kolejnych, rozpatrywanych tworzyw azotkowych. Naprężenie normalne do powierzchni próbki wyznaczone dla ziaren \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\), pomimo zachodzącej częściowej relaksacji, we wszystkich analizowanych materiałach było naprężeniem ściskającym. Podobnie w przypadku kompozytu \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-SiC}\), wyznaczone wartości naprężenia normalnego dla wtrąceń \(\text{SiC}\) były, w zakresie błędu pomiarowego, zgodne z wartościami uzyskanymi w symulacjach (\(\sim\)250 MPa). Istotne różnice pojawiły się w przypadku kompozytu \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\). Wartość naprężenia normalnego dla wtrąceń \(\text{TiN}\) wyznaczona doświadczalnie wynosiła \(\sim\)−171 MPa. Tak duża różnica między wartością wyznaczoną doświadczalnie a wartością uzyskaną w symulacjach, świadcząca o zmianie charakteru naprężenia (ściskanie, SKP – rozciąganie, MES) mogła być wynikiem relaksacji naprężeń występujących na powierzchni tego tworzywa zachodzącej poprzez pękanie. Obserwacje te potwierdziły zatem przypuszczenie o możliwości inicjacji mikropęknięć, które w kompozycie \(\text{Si}_{\text{3}}\text{N}_{\text{4}}\text{-TiN}\) mogą odpowiadać za wysoką odporność na kruche pękanie.
Ostatnim przykładem prac własnych, w których wykorzystane zostały modele 3D, są badania przeprowadzone dla polikryształów \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\), 3Y-TZP oraz ich kompozytów ziarnistych [771]. Głównym celem tych badań było wyznaczenie wartości współczynników rozszerzalności cieplnej dla litych tworzyw na podstawie symulacji opartych o trójwymiarowe rekonstrukcje mikrostruktury. Ilościowy charakter tej pracy wymagał, aby na każdym etapie budowy modelu obliczeniowego, wykorzystywany był jak najwierniejszy opis materiału. Stąd też wynikał dobór tworzyw, które zostały wykorzystane w pracy. Tlenek glinu oraz tlenek cyrkonu, należą do materiałów, dla których zgromadzona została duża liczba wysokiej jakości danych doświadczalnych, dotyczących ich właściwości podstawowych. Pozwalało to z jednej strony na wykorzystanie w modelach, dobrze zweryfikowanych parametrów materiałowych, a z drugiej, na późniejsze porównanie uzyskanych wyników symulacji zarówno z wynikami pomiarów własnych, jak również z danymi zaczerpniętymi z obszernej literatury tematu.
Sama rekonstrukcja budowy wewnętrznej, wykorzystująca parametry mikrostrukturalne uzyskane klasycznymi metodami stereologicznymi i zrealizowana przy pomocy teselacji Laguerre’a, została opisana już wcześniej (w p. 4.3.4). Uzyskane tą drogą modele geometryczne były statystycznie równoważne rzeczywistej mikrostrukturze rozpatrywanych tworzyw, a narzucona periodyczność geometrii, pozwoliła na zastosowanie podczas symulacji, periodycznych warunków brzegowych (zob. p. 4.3.5). Wykorzystane w pracy parametry materiałowe takie jak: osiowe współczynniki rozszerzalności cieplnej oraz współczynniki sztywności, zostały przyjęte na podstawie danych referencyjnych dla monokryształów oraz wcześniej przeprowadzonych pomiarów własnych [25]. Dzięki temu, w modelach materiałowych, uwzględniona została anizotropia właściwości termomechanicznych krystalitów. Podczas symulacji zjawiska rozszerzalności cieplnej, opracowana została procedura pozwalająca na oszacowanie rozmiaru SVE (zob. p. 3.4.2), co pozwoliło na zebranie wyników dla reprezentatywnej próby realizacji.
Uzyskiwane wyniki symulacji (łącznie, w trakcie pracy, przeprowadzone zostały symulacje dla kilkuset realizacji), były walidowane na podstawie wyników pomiarów dylatometrycznych. Pomiary te zostały wykonane kilkukrotnie dla próbek reprezentujących wszystkie badane układy: zarówno jednofazowe spieki \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\), 3Y-TZP jak i układy kompozytowe, zawierające różny udział objętościowy faz \(\alpha\text{-Al}_{\text{2}}{\text{O}}_{\text{3}}\) i 3Y-TZP (15, 35, 50 % obj.). Uzyskana w pomiarach dylatometrycznych niepewność wyznaczenia współczynników rozszerzalności cieplnej zawierała się w zakresie od ± 0.1 × 10−6 / °C dla kompozytu AZ15 (\(\text{Al}_{\text{2}}{\text{O}}_{\text{3}}\) z 15 % obj. TZP) do ± 0.4 × 10−6 / °C dla TZP (przy 95 % poziomie ufności). Wyniki uzyskane na podstawie symulacji oraz dane z pomiarów dylatometrycznych, wykorzystane do walidacji, przedstawione zostały na rysunku 4.13.
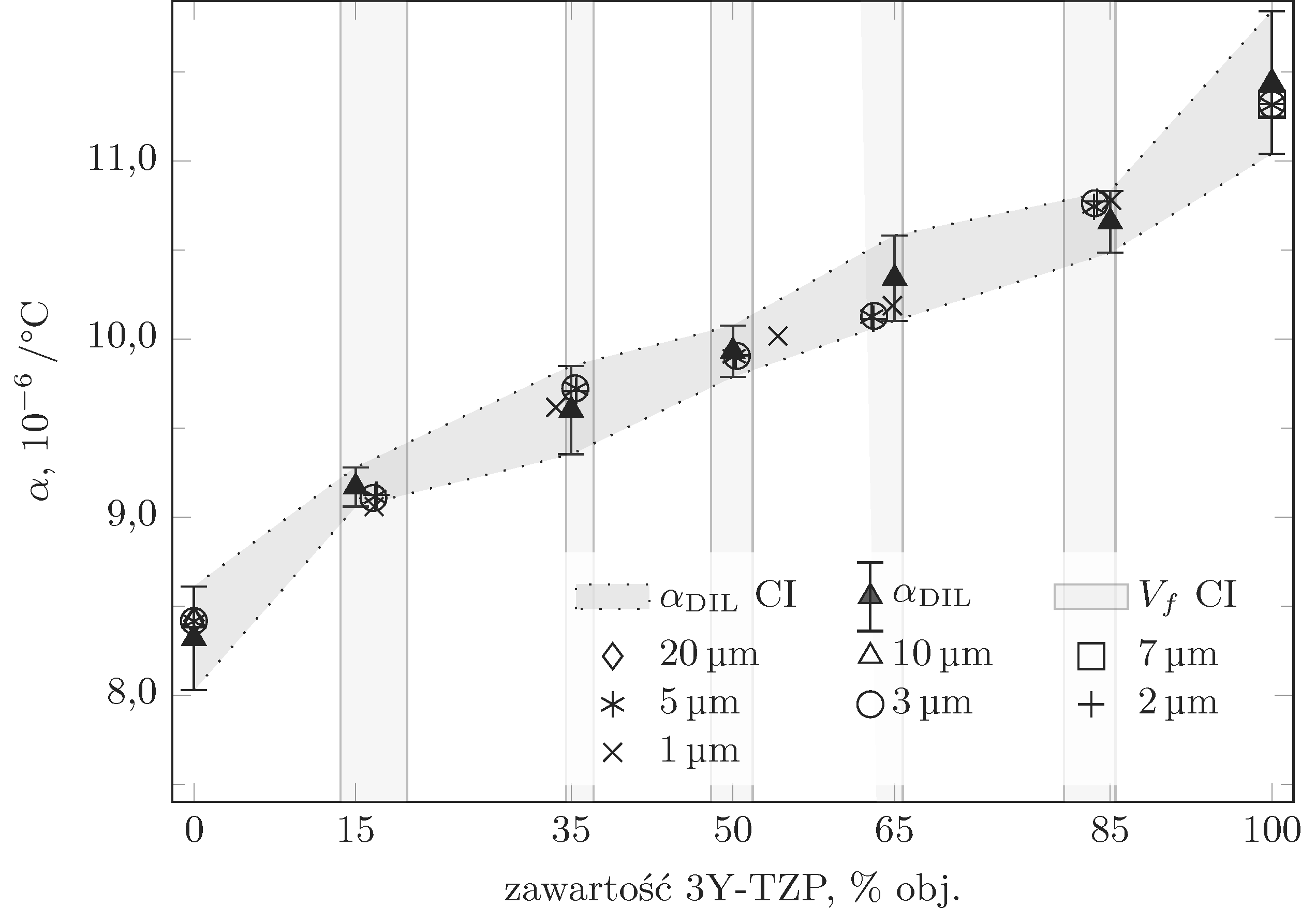
Dla wszystkich badanych materiałów, uzyskane w symulacjach wartości współczynników rozszerzalności cieplnej, mieściły się w zakresie błędu wyznaczonego dla pomiarów doświadczalnych. Rozbieżność wyników nie przekraczała 2 %. Tak duża dokładność symulacji przeprowadzonych na skonstruowanych w trakcie pracy modelach obliczeniowych, potwierdza ich przydatność w badaniach ilościowych dla polikrystalicznych materiałów ceramicznych. Opisana ścieżka, pozwalająca na przygotowanie reprezentatywnego zespołu realizacji, umożliwia zatem uzyskiwanie wiarygodnych wyników dotyczących makroskopowych właściwości termomechanicznych, na podstawie niewielkiego zestawu danych wejściowych. Podejście to może być więc wykorzystywane zarówno w badaniach podstawowych jak również w zakresie optymalizacji składu czy projektowania nowych tworzyw ceramicznych.
Przedstawione w tym rozdziale przykłady modeli numerycznych opartych na wirtualnych mikrostrukturach polikryształów i kompozytów ziarnistych, ilustrują jedynie niewielki zakres zagadnień, leżących w obszarze zainteresowań obliczeniowej inżynierii materiałowej. Wybór ten został jednak dokonany w oparciu o prace własne, które były prowadzone z zastosowaniem metody elementów skończonych i pozwoliły na realizację wielu tematów badawczych dotyczących analizy właściwości termomechanicznych tworzyw ceramicznych. Z tego względu, opisane tutaj rozwiązania i techniki stosowane do przygotowania modeli obliczeniowych, mogą zostać z powodzeniem wykorzystane zarówno w badaniach podstawowych, jak i w pracach inżynierskich, dotyczących optymalizacji czy modyfikacji właściwości sprężystych i cieplnych polikrystalicznych materiałów ceramicznych. Niektóre z zaprezentowanych rozwiązań, mogą również posłużyć do symulacji o charakterze ilościowym.
Takie analizy numeryczne, umożliwiające oszacowanie jakościowe i ilościowe wybranych właściwości tworzyw, mogą zatem pozwolić na ograniczenie zakresu badań doświadczalnych, przyspieszyć je i tym samym obniżyć koszty wdrożenia nowych i modyfikacji już istniejących materiałów. Podejście takie może być szczególnie pomocne w przypadku tworzyw ceramicznych, dla których proces przygotowania substratów (synteza proszków, uzyskanie wymaganego uziarnienia, granulacja, itd.), następnie optymalizacja warunków spiekania i na końcu etap przygotowania testowych próbek do badań weryfikujących, są wyjątkowo czasochłonne. Dlatego dokonanie eliminacji liczby wariantów (opracowywanych i badanych składów), już na etapie wstępnym, podczas ustalania zakresu badań, może prowadzić do znaczącej poprawy efektywności dalszych prac laboratoryjnych.
Szersze wykorzystanie metod numerycznych w tym zakresie, czy wręcz wprowadzenie wspomagania komputerowego w proces projektowania, wymaga jednak dalszej poprawy jakości i rozszerzenia zakresu badań, które mogą zostać przeprowadzone in silico. Niezbędne jest również przełamanie bariery wynikającej z wciąż ograniczonego zaufania środowiska badawczego, ale również przemysłowego, do wyników symulacji numerycznych prowadzonych w obszarze badań, które tradycyjnie realizowane są metodami doświadczalnymi i stanowią fundament klasycznej inżynierii materiałowej. Dlatego rozdział ten, będący podsumowaniem całości zagadnień przedstawionych w monografii, został poświęcony przedstawieniu technik przygotowania zarówno prostych modeli 2D jak i bardziej zaawansowanych modeli 3D, które pozwalają na uzyskanie użytecznych informacji o materiale, uzupełniających albo rozszerzających te, które można osiągnąć metodami doświadczalnymi. Stąd też sposób prezentacji wyników prac własnych, został dobrany tak, aby przekazać przede wszystkim, jak najwięcej informacji o technikach pozwalających na uzyskanie modeli obliczeniowych, umożliwiających realizację różnych celów badawczych. Konkretne rezultaty uzyskane na podstawie symulacji prowadzonych na opracowanych tymi technikami modelach, które zostały tutaj również zawarte, mają więc raczej charakter ilustracyjny. Szczegółowe opracowania danych, w odniesieniu do rozpatrywanych w pracach własnych tworzyw, zawarte są w cytowanych publikacjach. Mam nadzieję, że takie podejście do prezentacji wyników zebranych przeze mnie w ostatnich kilkunastu latach, będzie bardziej użyteczne i pozwoli zainteresować obliczeniową inżynierią materiałową, większą grupę badaczy i inżynierów.