Instrukcje do ćwiczeń laboratoryjnych

Przeprowadzając próbę rozciągania masz ponadto możliwość obserwacji przebiegu rozciągania i oceny jakościowej i ilościowej tego procesu. Ze względu na możliwość określenia podczas tej próby wielu istotnych własności materiałowych i na prostotę wykonania jest to podstawowa próba wytrzymałościowa metali. Warunki przeprowadzania statycznej próby rozciągania metali są sprecyzowane przez normy: PN-80/H-04310, PN-77/H-04307, PN-84/H-04308.

Ze względów dydaktycznych odstąpiono w niektórych elementach tego ćwiczenia od warunków narzuconych przez normy.

2. Maszyna wytrzymałościowa

Próbę rozciągania wykonasz na uniwersalnej maszynie wytrzymałościowej o napędzie mechanicznym, której schemat pokazano na rysunku 1.1. Zasada pracy maszyny jest następująca: silnik elektryczny poprzez układ przekładni uruchamia obracającą się nakrętkę. Nakrętka wprawia w ruch śrubę pociągową (2), która przemieszcza dolny uchwyt szczękowy (5). Próbka zamocowana w uchwytach jest rozciągana. Górny uchwyt (8) połączony jest poprzez układ dźwigni z dźwignią uchylną siłomierza, na której znajduje się obciążnik (12).

1-1a

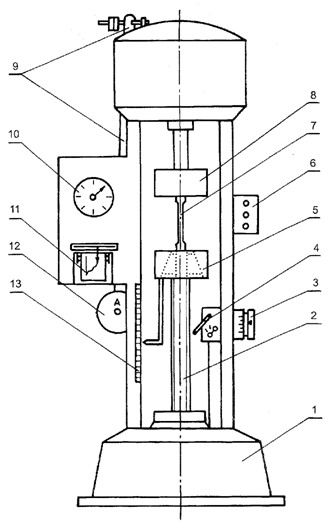
Rys. 1.1. Maszyna wytrzymałościowa używana do próby rozciągania: 1 – korpus maszyny, 2 – śruba, 3 – nastawnik, 4 – korba, 5 – uchwyt szczękowy, 6 – przyciski sterownicze, 7 – badana próbka, 8 – uchwyt szczękowy, 9 – układ dźwigniowy, 10 – tarcza siłomierza, 11 – rejestrator, 12 – wymienny obciążnik, 13 – listwa pomiarowa

Jego ciężar decyduje o zakresie pomiarowym. Obciążniki oznaczone są A, B, C, tak samo jak odpowiadające im skale na tarczy siłomierza. Wychylenie dźwigni siłomierza jest przenoszone poprzez układ zębatek na wskazówkę siłomierza i na pisak rejestratora. Kąt obrotu bębna rejestratora jest proporcjonalny do wydłużenia próbki. W ten sposób uzyskuje się wykres siły rozciągającej w funkcji wydłużenia próbki.

Sterowanie maszyną odbywa się za pomocą przełącznika oraz przycisków (6). Przełącznik służy do ustawienia wybranego rodzaju ruchu spośród następujących:

– ruch manewrowy (szybki),

– ruch roboczy,

– napęd ręczny.

Rozciąganie z napędem ręcznym odbywa się za pomocą korby (4) obracanej w lewo.

Uwaga!

Należy szczególne uważać, aby maszyna nie była obciążana w trakcie ruchu manewrowego. Ruch manewrowy można stosować wyłącznie dla przesuwania nie obciążonych uchwytów szczękowych. Przełącznik ruchów należy przestawiać tylko przy wyłączonym napędzie.

3. Tensometr mechaniczny

Tensometr mechaniczny, którego schemat pokazano na rysunku 1.2, służy do pomiarów wydłużenia próbki na danym odcinku. Elementami mierzącymi są czujniki zegarowe o działkach elementarnych 0,01 mm. Tensometr mocuje się na próbce za pomocą dwóch par ostrzy, z których dolna para osadzona jest przegubowo, tworząc dźwignie równoramienne. Dźwignie te powodują przesunięcie trzpieni czujników zegarowych o odcinek równy odkształceniu próbki.

Uwaga!

Należy delikatnie obchodzić się z tensometrem i dokładnie zamocować go na próbce.

1-2c

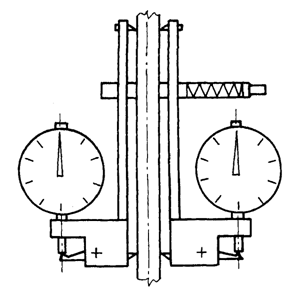
Rys. 1.2. Tensometr mechaniczny z czujnikami zegarowym

4. Wykres rozciągania

Podczas rozciągania badaną (rys. 1.3) próbkę poddaje się działaniu jednoosiowego obciążenia, mierząc jednocześnie siłę rozciągającą i wydłużenie próbki. Wykres zarejestrowany automatycznie przez rejestrator podczas próby odwzorowuje przebieg rozciągania w układzie siła-wydłużenie. Wykres rozciągania w układzie naprężenie-wydłużenie względne ma nieco inny kształt. Pierwszy nazywamy wykresem umownym lub technicznym, drugi - rzeczywistym wykresem rozciągania.

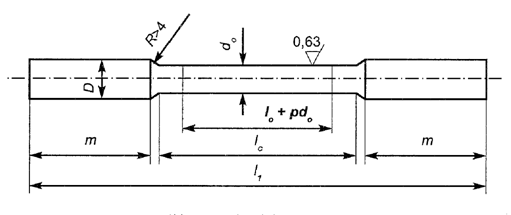
1-3d120

Rys. 1.3. Próbka z główkami do chwytania w szczęki

Na wykresach rozciągania metali, przedstawionych na rysunku 1.4, wyróżnić można kilka charakterystycznych punktów:

1. Granica proporcjonalności. Jest to naprężenie, do którego występuje proporcjonalność naprężenia do wydłużenia jednostkowego. Wyznacza się ją wg wzoru

(P_H) jest siłą odpowiadającą końcowi prostoliniowego odcinka wykresu rozciągania (rys. 1.5,) a (S₀) przekrojem początkowym. Granica proporcjonalności jest granicą stosowalności prawa Hooke’a.

2. Granica sprężystości. Granicy tej towarzyszy pojawienie się odkształceń trwałych. Niezwykle trudno jest zarejestrować dokładnie wartość naprężenia, przy którym pojawiają się pierwsze odkształcenia trwałe. Dlatego przyjęto, że materiał ma wartości sprężyste do umownej granicy sprężystości. Umowną granicę sprężystości (R_0,05) zdefiniowano jako wartość naprężenia rozciągającego, które wywołuje wydłużenie trwałe = 0,05% pierwotnej długości pomiarowej próbki

Po obciążeniu próbki siłą (P_0,05) i po jej odciążeniu powinno pozostać wydłużenie 0,05% pierwotnej długości pomiarowej próbki.

Wydłużenie całkowite jest sumą wydłużenia liniowego i nieliniowego. Przyjmując, że wydłużenie liniowe jest nietrwałe a wydłużenie nieliniowe jest trwałe, (P_0,05) można wyznaczyć z wykresu rozciągania, jako siłę wywołującą wydłużenie nieliniowe = 0,05% pierwotnej długości pomiarowej próbki (rys. 1.4).

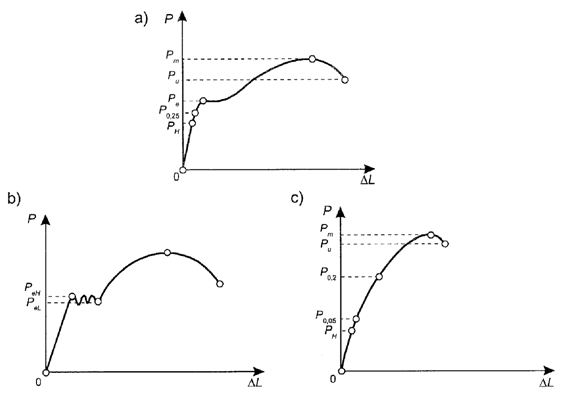
1-4d120

Rys. 1.4. Wykresy rozciągania dla materiałów: a) wykazujących wyraźną granicę plastyczności, b) wykazujących górną i dolną granicę plastyczności, c) bez wyraźnej granicy plastyczności

3. Wyraźna granica plastyczności. Występuje na wykresach rozciągania materiałów elastoplastycznych, jak np. stal niskowęglowa. Jest to naprężenie rozciągające, po osiągnięciu którego obserwuje się wyraźny wzrost długości rozciąganej próbki bez wzrostu obciążenia

Jeżeli w okolicach granicy plastyczności następuje wyraźna oscylacja naprężenia, to wyróżnia się górną i dolną granicę plastyczności. Naprężenia rozciągające, odpowiadające pierwszemu szczytowi obciążenia siłą rozciągającą (P_eH), po którym następuje jej spadek, nazywane jest górną granicą plastyczności

Naprężenie rozciągające odpowiadające najmniejszej wartości siły (P_eL) po której następuje ciągły wzrost siły, nazywa się dolną granicą plastyczności

1-5a

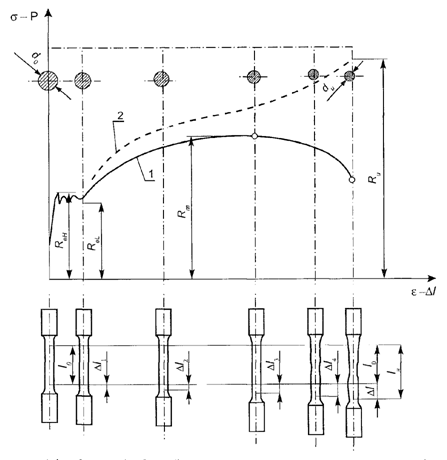
Rys. 1.5. Wykres rozciągania stali miękkiej. Krzywa l jest odniesiona do przekroju pierwotnego próbki (S₀). Krzywa 2 jest odniesiona do przekroju rzeczywistego próbki (S_u).

4. Umowna granica plastyczności. Określa się ją tylko dla materiałów nie mających wyraźnej granicy plastyczności, jak np. stal wysokowęglowa i żeliwo. Umowna granica plastyczności służy jako kryterium porównawcze do oceny materiałów. Określa się ją jako wartość naprężenia rozciągającego, które wywołuje w próbce wydłużenie trwałe = 0,2% pierwotnej długości pomiarowej próbki

Sposób wyznaczania (P_0,2) z wykresu rozciągania przedstawiono na rysunku 1.6. Jest on podobny do sposobu wyznaczania (R_0,05).

1-6c

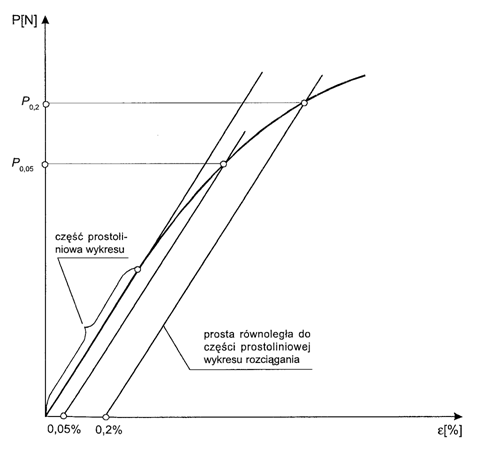
Rys. 1.6. Sposób wyznaczania umownej granicy plastyczności i sprężystości

5. Wytrzymałość na rozciąganie. Jest to naprężenie rozciągające, przy którym siła obciążająca uzyskuje maksymalną wartość (P_m)

Odkształcenie na długości próbki przestaje być jednorodne, tworzy się miejscowe przewężenie, tzw. szyjka. W tych częściach próbki, które zachowały kształt cylindryczny nadal panuje jednoosiowy stan naprężeń. W samej zaś szyjce stan naprężeń jest trójosiowy.

6. Naprężenia rozrywające. Jest to naprężenie występujące w przekroju poprzecznym próbki w miejscu przewężenia, w chwili jej rozerwania

Jest to naprężenie rzeczywiste, odniesione do aktualnego przekroju próbki (S_u).

Poprzednie granice obliczono dzieląc wartość siły obciążającej przez pole przekroju początkowego próbki. Przekrój próbki podczas rozciągania stale się zmniejsza. W zakresie odkształceń sprężystych zmniejszenie próbki jest pomijalnie małe, lecz dalej staje się znaczące. Skutkiem tego, naprężenie rzeczywiste odniesione do przekroju aktualnego (P/S_u) jest wyraźnie większe od naprężenia obliczanego jako iloraz siły obciążającej do przekroju początkowego (P/S₀).

Trzeba pamiętać, ze mimo iż granice odnoszone do przekroju początkowego definiowano jako naprężenia, są to jedynie naprężenia obliczeniowe lub stałe materiałowe w jednostkach naprężenia.

5. Określenie własności plastycznych

Do oceny własności plastycznych materiału, rozumianych jako zdolność do trwałych odkształceń, służy wydłużenie względne (A₁₀) oraz przewężenie względne (Z). Indeks „10” przy A oznacza, że wydłużenie względne zbadano na próbkach proporcjonalnych dziesięciokrotnych, czyli takich, dla których długość pomiarowa jest dziesięć razy większa od średnicy:

gdzie:

l₀ – początkowa długość pomiarowa,

l_u – długość pomiarowa po zerwaniu,

d₀ – średnica początkowa próbki,

d_u – średnica próbki po próbie w miejscu zerwania.

6. Próbki

Będziecie badać dwie jednakowe próbki proporcjonalne, dziesięciokrotne, z tego samego metalu, o kształtach i wymiarach jak na rysunku 1.3. Należy pamiętać, że aby rezultaty próby rozciągania były porównywalne, warunki przeprowadzenia próby, w tym również kształty i wymiary próbek, muszą być unormowane.

7. Plan ćwiczenia

Twoim zadaniem jest przeprowadzenie próby rozciągania dwóch próbek z tego samego metalu.

W trakcie rozciągania pierwszej stwierdzisz, jaki charakter ma wykres rozciągania danego materiału, czy wykazuje wyraźną granicę plastyczności. Zbierzesz również dane potrzebne do określenia (Z), (A),(P_m), (R_m), (R_e), (R_eH, R_eL).

Próbę rozciągania drugiej próbki przeprowadzisz z założonym na próbkę tensometrem. Na podstawie jego wskazań sporządzisz później wykres zależności siły rozciągającej i wydłużenia.

Wykres ten będzie znacznie dokładniejszy od wykresu z rejestratora. Korzystając z niego określisz (R_H), (R_0,05), (R_0,2).

Aby nie zniszczyć tensometru nie można dopuścić do rozerwania próbki, na którą założony jest tensometr. Trzeba zatem na podstawie pierwszej próby określić bezpieczną siłę, do której można pozostawić tensometr na próbce. Przyjmij, że dla wykresów z wyraźną granicą plastyczności siłą tą jest P_e, a dla wykresów bez wyraźnej granicy plastyczności (0,7 P_m).

Wydłużenie będziesz odczytywał z czujników tensometru z dokładnością 0,01 mm. Pozostałe pomiary długości odczytaj z dokładnością działki elementarnej odpowiedniej skali na tarczy siłomierza.

8. Tok przeprowadzania ćwiczenia

a) W środkowej części pierwszej próbki zaznacz dwiema ryskami odcinek pomiarowy o długości około 100 mm. Zmierz długość zaznaczonego odcinka pomiarowego (l₀) i średnicę początkową próbki (d₀).

b) Umieść pierwszą próbkę w szczękach uchwytów zrywarki. Ustaw ruch roboczy i przeprowadź rozciąganie próbki aż do zerwania, z automatyczną rejestracją procesu na taśmie papierowej.

c) Odczytaj siły (P_e) i (P_m).

d) Zmierz długość pomiarową próbki po rozerwaniu (l_u). W tym celu złóż jej obie części tak, aby przylegały do siebie i zmierz odległość pomiędzy ryskami. Jeżeli rozerwanie nastąpi w pobliżu rysek lub poza nimi, należy zrezygnować z określania (l_u) i (A₁₀). Zmierz średnicę próbki w miejscu zerwania (d_u).

e) Zmierz średnicę początkową (d₀) drugiej próbki. Umieść ją w szczękach uchwytów i starannie załóż na niej tensometr. Zmierz odległość pomiędzy ostrzami tensometru. Jest to początkowa długość pomiarowa próbki drugiej (l₀).

f) Określ bezpieczną wartość siły, do której można pozostawić tensometr na próbce, równą (P_e) lub (0,7 P_m), gdzie (P_e) i (P_m) wzięte z poprzedniej próby. Rozciągaj próbkę na ręcznym napędzie do bezpiecznej wartości siły, zdejmując w tym czasie około 15 pomiarów wydłużenia i siły. Rozpocznij notowanie pomiarów, gdy siłomierz będzie wskazywał 0.

g) Zdejmij tensometr z próbki. Obciążaj dalej próbkę przy pomocy napędu mechanicznego ruchem roboczym aż do zerwania.

h) Uporządkuj stanowisko.

9. Zestawienie pomiarów

Materiał próbek:

Pierwsza próbka:

d₀ = . . . . . . . . . [mm],

l₀ = . . . . . . . . . [mm],

d_u = . . . . . . . . . [mm],

l_u = . . . . . . . . . [mm],

P_m = . . . . . . . . . [N].

Wykres rozciągania zarejestrowany automatycznie.

Druga próbka:

d₀ = . . . . . . . . . [mm],

l₀ = . . . . . . . . . [mm].

Tabela 1.1 zawiera zestawienie wyników próby rozciągania drugiej próbki.

Tabela 1.1. Wyniki próby rozciągania

Lp.

Siła

P

[N]

Wskazania czujników

[10^-2 mm]

Przyrosty

[10^-2 mm]

Wydłużenie

Δl

[mm]

l₁ lewy

l₂ prawy

Δl₁

Δl₂

(Δl₁)i (Δl₂)są przyrostami wskazań czujników. Oblicza się je odejmując od wskazań czujników wskazania początkowe, przy których wartość siły (P) wynosiła zero.

średnia arytmetyczna przyrostów.

10. Opracowanie wyników

a) Na podstawie wyników próby rozciągania pierwszej próbki oblicz wg wzorów zamieszczonych wcześniej:

– S₀, S_u,

– R_e lub R_eH i R_eL,

– R_m,

– Z,

– A₁₀.

b) Wyskaluj wykres rozciągania z rejestratora. Odczytaj z niego (P_u), oblicz (R_u).

c) Na podstawie wyników próby rozciągania drugiej próbki wypełnij odpowiednią tabelę (tab. 1.1).

d) Sporządź wykres P = P(l). Korzystając z niego określ:

– P_H,

– P_0,05,

– P_0,2 jeśli nie ma wyraźnej granicy plastyczności.

Sposób wyznaczania (P_H), (P_0,05) i (P_0,2) opisano wcześniej. Oblicz:

– S₀ dla drugiej próbki,

– R_H,

– R_0,05,

– R_0,2 jeśli nie ma wyraźnej granicy plastyczności.

e) Zastanów się, w jaki sposób można określić i określ moduł sprężystości podłużnej (E) na podstawie próby rozciągania drugiej próbki.

f) Porównaj rezultaty z wartościami w tabelach. Przeprowadź dyskusję wyników.

g) Jeżeli wyznaczenie jakiejś wielkości okaże się niemożliwe lub otrzymane wyniki budzą twoje wątpliwości, spróbuj wyjaśnić ich przyczynę. Opisz twoje spostrzeżenia i uwagi po przeprowadzeniu próby.

Pytania

1. Narysuj wykres rozciągania stali miękkiej w układzie (P – Δl) i (σ – ε). Zaznacz punkty charakterystyczne.

2. Narysuj wykres rozciągania stali hartowanej w układzie (P – Δl) i (Δσ – ε). Zaznacz punkty charakterystyczne.

3. Wyjaśnij różnicę kształtu wykresu rozciągania w układach (P – Δl) i w układzie (σ – ε). Czy pomiary, które wykonałeś pozwalają na wykonanie dokładnego wykresu (σ – ε)?

4. Uzasadnij sposób określenia umownej granicy sprężystości i plastyczności zilustrowany na rysunku 1.6.

5. Czy prędkość rozciągania i temperatura, w której przeprowadzana jest próba mają wpływ na rezultaty?

Spis treści

Powrót do początku ćwiczenia

Ćwiczenie 2. Próba statyczna ściskania materiałów kruchych

1. Cel ćwiczenia

Określenie dla materiału użytego w doświadczeniu:

– wytrzymałości na ściskanie (R_c),

– modułu Younga (E).

Próbę statycznego ściskania stosuje się głównie przy badaniu materiałów kruchych, czyli nie wykazujących zdolności do znacznych odkształceń plastycznych (beton, cegła, skały). Istnieją normy dla próby ściskania żeliwa szarego i materiałów kamiennych.

Materiały kruche mają znacznie większą wytrzymałość na ściskanie (R_c) niż wytrzymałość na rozciąganie (R_m):

– dla betonu R_c = (5-20) R_m,

– dla granitu R_c = (40-70) R_m,

– dla piaskowca R_c = (20-70) R_m.

Cechą, która charakteryzuje materiały kruche jest właśnie wytrzymałość na ściskanie (R_c)

gdzie:

l₀ – początkowa długość pomiarowa,

P_c – największa wartość obciążenia ściskającego, przy którym następuje rozkruszenie próbki,

F₀ – pole początkowego przekroju próbki.

Jeżeli wykres ściskania l = f(P) ma część, w której skrócenie (l) jest wprost proporcjonalne do siły ściskającej (P), to na tej podstawie wyznaczamy dla tego materiału moduł Younga (E).

Jeżeli zależność ta nie jest wprost proporcjonalna, to na podstawie kilku pierwszych wyników (gdzie w przybliżeniu można przyjąć, że materiał zachowuje się liniowo-sprężyście) wyznaczamy wartość średnią modułu Younga (E).

Wartość modułu Younga wyznacza się z prawa Hooke’a

gdzie:

P – siła ściskająca,

Δl – skrócenie próbki odpowiadające sile (P),

l – początkowa wysokość próbki,

F₀ – pole powierzchni początkowego przekroju próbki.

2. Aparatura pomiarowa

Ćwiczenie przeprowadzasz na maszynie wytrzymałościowej przedstawionej na rysunku 2.1. Ruch roboczy maszyny realizuje się w następujący sposób: silnik elektryczny porusza pompę wytwarzającą ciśnienie oleju w cylindrze (2). Ciśnienie działające na tłok (3) powoduje przesunięcie płyty (4). Siła wytwarzana w cylindrze (2) jest przenoszona również na płytę (9) i (7) przez pręty (5), a następnie na próbkę (8). Ściskanie próbki przeprowadzasz w ruchu roboczym maszyny.

Ruchem manewrowym następuje ustawienie płyty (7) na odpowiedniej wysokości, w celu dostosowania odległości między płytami (7) i (4) do wymiarów badanej próbki. Ustawienie to realizowane jest za pomocą prętów (6). Po ustawieniu płyty (7) na odpowiedniej wysokości, umieszcza się próbkę (8) między płytami (4) i (7) i włącza się napęd pompy tłoczącej olej do cylindra (2). Rozpoczyna się ruch roboczy maszyny.

2-1c

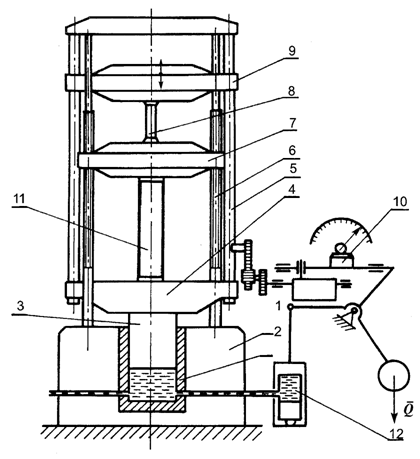
Rys. 2.1. Uniwersalna maszyna wytrzymałościowa: l – korpus maszyny, 2 – cylinder, 3 – tłok, 4 – belka dolna, 5 – pręty łączące, 6 – pręty śrubowe, 7 – belka nośna, 8 – badana próbka, 9 – belka górna, 10 – tarcze siłomierza, 11 – cylinder pomiarowy

Do pomiaru wielkości siły działającej na badaną próbkę służy specjalny system hydrauliczno-mechaniczny. Najważniejszym elementem tego systemu jest cylinder pomiarowy (12), połączony hydraulicznie z cylindrem roboczym (2). Siła działająca na tłok w cylindrze po- woduje odpowiednie, proporcjonalne do siły wychylenie wskazówki siłomierza (10).

3. Pomiar skrócenia próbki

Pomiar skrócenia próbki przeprowadza się w sposób przedstawiony na rysunku 2.2. Polega on na pomiarze przemieszczenia płyty maszyny wytrzymałościowej w stosunku do drugiej płyty, którą traktujemy jako nieruchomą, w sytuacji gdy między płytami znajduje się ściskana próbka. Pomiarów dokonuje się za pomocą trzech czujników zegarowych. Wartość skrócenia (Δl) oblicza się jako wartość średnią skrócenia (Δl₁, Δl₂, Δl₃) odczytanego na poszczególnych czujnikach. Czujniki zegarowe stosowane w tym ćwiczeniu mają dokładność 0,01 mm.

2-2a

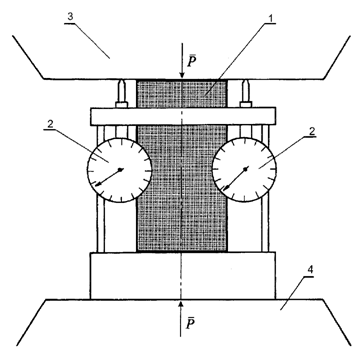
Rys. 2.2. Schemat pomiaru skrócenia próbki: 1 – badana próbka, 2 – czujniki zegarowe, 3 – górna płyta maszyny wytrzymałościowej, 4 – dolna płyta maszyny wytrzymałościowej

4. Tok przeprowadzenia ćwiczenia

1. Określ pole przekroju poprzecznego i wysokość próbki.

2. Przeprowadź dwie próby ściskania:

a) pierwszą próbkę ściskaj bez przeprowadzenia pomiarów jej skrócenia, zarejestruj jedynie siłę, przy której próbka uległa zniszczeniu. Na tej podstawie określ, co jaką wartość siły będziesz odczytywał wartości skrócenia, ściskając drugą próbkę tak, aby 1iczba uzyskanych wyników (skrócenie w funkcji siły) była nie mniejsza od 15. Przy podziale na 15 odcinków pomiarowych, weź pod uwagę 70% wartości siły, przy której pierwsza próbka uległa zniszczeniu!

b) ściskając drugą próbkę rejestruj wielkość skrócenia i odpowiadającą mu wartość siły; zarejestruj również siłę, przy której próbka uległa zniszczeniu (wcześniej, po dokonaniu około 15 pomiarów, usuń czujniki zegarowe, aby nie uległy one uszkodzeniu w momencie niszczenia próbki!).

5. Opracowanie wyników

Sprawozdanie z ćwiczenia powinno zawierać:

– wykres Δl = f(P),

– wypełnione tabele 2.1, 2.2, 2.3,

– wartości tablicowe (R_c) i (E) materiału badanego w ćwiczeniu, wnioski i uwagi z przeprowadzonego ćwiczenia.

Tabela 2.1

Nr pomiaru

Siła ściskająca

[N]

Wielkość skrócenia próbki

[mm]

l₁

Δl₁

ΣΔl₁

l₂

Δl₂

ΣΔl₂

l₃

Δl₃

ΣΔl₃

ΣΔl_śr

l₁, l₂, l₃ – wskazania czujników odkształceń,

Δl₁, Δl₂, Δl₃ – przyrosty wskazań odkształceń

Tabela 2.2

Siła ściskająca

Skrócenie próbki

Δl

Moduł Younga

Wartość średnia modułu Younga

E_śr

[N]

[mm]

[MPa]

Tabela 2.3

Siła, przy której nastąpiło zniszczenie próbki [N]	P₀
Pole pierwotnego przekroju próbki [mm²]	F₀
Wytrzymałość na ściskanie [MPa]	R_c
Początkowa wysokość próbki [mm]	l

Pytania

1. Wyjaśnij pojęcie wyboczenia pręta ściskanego.

2. Jak wygląda wykres ściskania materiału o dużej plastyczności np. miedzi, czy dla takich materiałów możemy określić (R_c)?

Spis treści

Powrót do początku ćwiczenia

Ćwiczenie 3. Próba statyczna skręcania

1. Cel ćwiczenia

Wyznaczenie zależności f = f(M_s).

Określenie dla badanego materiału:

– modułu sprężystości postaciowej (G),

– granicy proporcjonalności postaciowej (R_pr)

– granicy sprężystości (R_sp),

– granicy plastyczności (R_e).

Pręty, które będziesz badał w ćwiczeniu są prętami o przekroju kołowym.

Zależność kąta skręcania (f) takiego pręta od momentu skręcającego (M_s) wyraża się wzorem

gdzie:

l – długość skręcanego pręta,

G – moduł sprężystości postaciowej materiału, z którego wykonany jest pręt,

J₀ – biegunowy moment bezwładności przekroju poprzecznego pręta.

Biegunowy moment bezwładności (J₀) przekroju kołowego wynosi

gdzie d oznacza średnicę przekroju.

Na podstawie wzoru (3.1) możemy obliczyć wartość modułu (G)

jeżeli znana jest wartość momentu skręcającego (M_s) i odpowiadającego mu kąta skręcania (f) dla zakresu sprężystego. Wartość momentu skręcającego (M_s) obliczamy wg wzoru

gdzie:

S – promień momentu skręcającego (patrz rys. 3.1),

Q – wielkość zadawanego przez Ciebie obciążenia.

3-1c

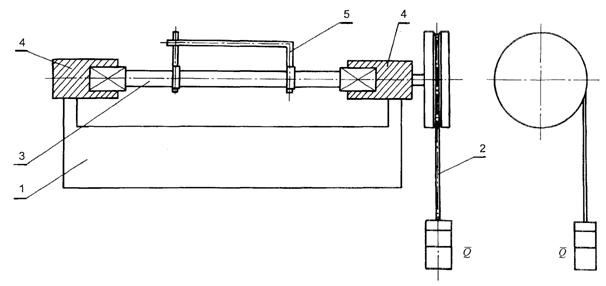
Rys. 3.1. Schemat urządzenia do skręcania pręta: l – korpus urządzenia, 2 – linka z ciężarkiem obciążająca próbkę, 3 – próbka, 4 – uchwyty mocujące próbkę, 5 – urządzenie do pomiaru kąta skręcenia próbki

Natomiast wielkość odpowiadającego mu kąta skręcenia (f) wynosi

gdzie:

R – odległość osi skręcanego pręta od osi wrzeciona czujnika,

x – przemieszczenie zarejestrowane przez czujnik (patrz rys. 3.2).

3-2c

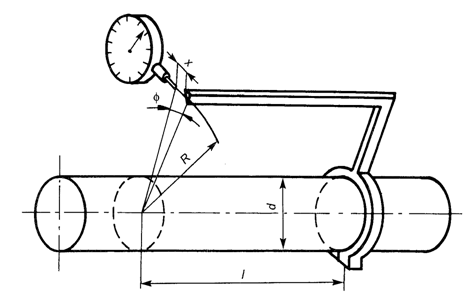
Rys. 3.2. Schemat urządzenia do pomiaru kąta skręcenia pręta

Granicę proporcjonalności (R_pr) wyznaczamy wg wzoru

gdzie:

S – promień momentu skręcającego (patrz rys. 3.1),

M_pr – moment skręcający, do wartości którego kąt skręcania (f) jest wprost proporcjonalny do momentu skręcającego,

– biegunowy wskaźnik wytrzymałości przekroju na skręcanie,

r – promień skręcanego pręta,

d – średnica skręcanego pręta.

Pręty, które badasz w ćwiczeniu, wykonane są z materiału sprężysto-plastycznego. Dla takiego materiału wyznacza się tzw. umowną granicę sprężystości (R_sp) i umowną granicę plastyczności (R_e):

gdzie: M_s_(0,075) i M_s_(0,3) są momentami skręcającymi odpowiadającymi trwałemu odkształceniu postaciowemu (g) włókien na zewnętrznej powierzchni pręta, o wartości odpowiednio: g = 0,075% i g = 0,3% (graficzną interpretację tych wielkości przedstawiają rys. 3.3 i 3.4).

3-3c

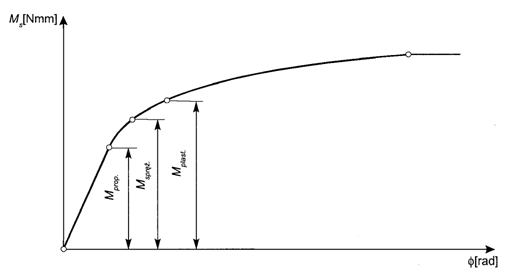
Rys. 3.3. Przykładowy wykres skręcania materiału sprężysto-plastycznego

Czyli przyjmuje się, że umowna granica sprężystości (R_sp) odpowiada trwałemu odkształceniu postaciowemu g = 0,00075, a umowna granica plastyczności (R_e) trwałemu odkształceniu postaciowemu g = 0,003.

Ponieważ

więc

A zatem, znając wartość kąta (f) odpowiadającego umownej granicy sprężystości (f = 0,00075 l/r) i umownej granicy plastyczności (f = 0,003 l/r) możesz, tak jak zostało to pokazane na rysunku 3.4, obliczyć wartość M_s_(0,075) i M_s_(0,3) i znając wskaźnik wytrzymałości przekroju na skręcanie (W₀) wyznaczyć (R_sp) i (R_e).

3-4c

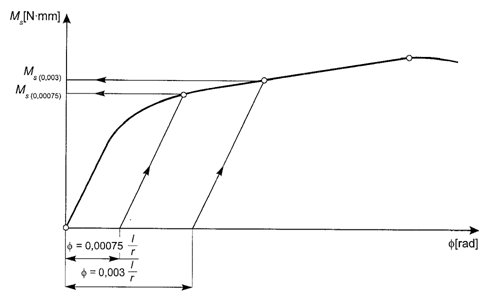
Rys. 3.4. Wykreślony sposób odczytania wartość M_s_(0,075) i M_s_(0,3)

2. Aparatura pomiarowa

Próbę skręcania prętów będziesz wykonywał na urządzeniu, którego schemat przedstawiono na rysunku 3.1. Zwiększając ciężar (Q) będziesz zwiększał wielkość momentu skręcającego (M_s) wywieranego na badaną próbkę.

3. Pomiar kąta skręcenia pręta

Pomiar kąta skręcenia pręta przeprowadza się w sposób pokazany na rysunku 3.2. Polega on na pomiarze za pomocą czujnika zegarowego, przemieszczenia (x) punktu leżącego na okręgu o promieniu (R). Przemieszczenie to odpowiada momentowi skręcającemu, wywołanemu zadanym obciążeniem (Q).

4. Tok przeprowadzenia ćwiczenia

Przeprowadź doświadczenie dla dwóch prętów wykonanych z różnych materiałów.

1. Określ wielkości (l, d, R, S).

2. Zamontuj na pręcie urządzenie do pomiaru kąta skręcenia (patrz rys. 3.1); na razie nie zakładaj jeszcze czujnika!

3. Umieść badany pręt w urządzeniu skręcającym.

4. Załóż i wyzeruj czujnik zegarowy (patrz rys. 3.2).

5. Obciążając próbkę kolejnymi ciężarkami odczytaj wskazania czujnika.

5. Opracowanie wyników

Sprawozdanie z ćwiczenia powinno zawierać:

– wykresy f = f(M_s),

– wypełnione tabele 3.1, 3.2, 3.3,

– wnioski i uwagi z przeprowadzonego ćwiczenia.

Tabela 3.1

	Pręt 1	Pręt 2
długość pomiarowa próbki l [mm]
średnica przekroju próbki d [mm]
promień ramienia pomiarowego R [mm]
promień momentu skręcającego S [mm]
moment bezwładności przekroju J₀ [mm⁴]
wskaźnik wytrzymałości przekroju W₀ [mm³]

Tabela 3.2

Lp.

M_s

G_śr

[N]

[Nmm]

[mm]

[rad]

[MPa]

Tabela 3.3

		Pręt 1	Pręt 2
f (0,075)	[rad]
f (0,3)	[rad]
M_pr	[Nmm]
M_s_(0,075)	[Nmm]
M_s_(0,3)	[Nmm]
R_pr	[MPa]
R_sp	[MPa]
R_e	[MPa]

Pytania

1. Określ stan naprężenia w pręcie skręcanym momentem (M_s).

2. Znając wartość naprężeń dopuszczalnych na skręcanie (k_s) oraz dopuszczalny kąt skręcenia wału (f_dop) oblicz średnicę wału.

3. Kiedy przy obliczaniu wałów korzystamy z warunku sztywności, a kiedy z warunku wytrzymałościowego; podaj te warunki.

Spis treści

Powrót do początku ćwiczenia

Ćwiczenie 4. Próba statyczna ścinania technologicznego

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie studenta z praktycznym sposobem wykonania próby ścinania technologicznego oraz wyznaczenie doraźnej wytrzymałości na ścinanie badanego materiału.

Ścinanie próbki rozumiane jest jako cięcie materiału dokonane przez siły tnące (rys. 4.1), o przeciwnych zwrotach, leżące w jednej płaszczyźnie (rys. 4.2). Teoretycznie warunek ten spełniałyby dwa nieskończenie cienkie ostrza. W rzeczywistości wnikanie w materiał noży o pewnej grubości powoduje rozsunięcie sił, które tworzą parę i wywołują w próbce naprężenia zginające.

W przekrojach ścinanych elementów konstrukcyjnych z reguły występują równocześnie naprężenia styczne od sił tnących i normalne od momentów zginających.

4-1c

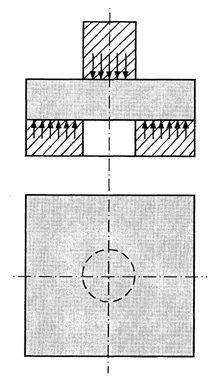
Rys. 4.1. Schemat ścinania cylindrycznego próbki

4-2a

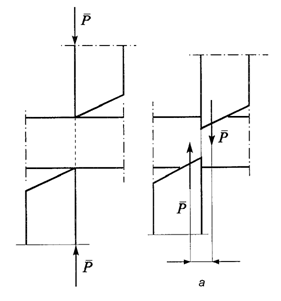
Rys. 4.2. Działanie ostrzy podczas ścinania technologicznego

Nie jest to zatem ścinanie czyste, lecz tzw. technologiczne. Sposób obciążenia próbki podczas próby ścinania również wywołuje złożony stan naprężenia.

Wytrzymałość na ścinanie (R₁) wyznacza się wg wzoru

gdzie:

P_t – największa siła podczas próby ścinania,

S – pole powierzchni ścinanej, obliczone wzorem

gdzie:

d – średnica sworznia,

g – grubość próbki.

Wzór ten opiera się na założeniu równomiernego rozkładu naprężeń tnących w ścinanych przekrojach i pominięciu naprężeń normalnych. Dla ścinania technologicznego założenie to jest dalekie od rzeczywistości.

Wytrzymałość na technologiczne ścinanie określone tym wzorem zależy nie tylko od własności wytrzymałościowych materiału próbki, lecz również od kształtu i wielkości przekroju ścinanego, wymiarów przyrządu i dokładności przylegania próbki. Określoną w powyższy sposób wytrzymałość (R_t) należy traktować jako wielkość umowną, dającą orientacyjną ocenę badanego materiału a nie jego rzeczywistą wytrzymałość na czyste ścinanie. Aby mogła służyć jako wielkość porównawcza, musi być wyznaczona w warunkach znormalizowanych (PN-68/H-04321).

2. Maszyna wytrzymałościowa

Do przeprowadzenia próby używa się maszyny wytrzymałościowej o napędzie hydraulicznym. Opis budowy, działania i obsługi maszyny znajduje się w ćwiczeniu nr 2.

3. Przyrząd do ścinania technologicznego

Przyrząd (rys. 4.3) składa się z: korpusu (1), wkręcanej tulei (2), pręta dociskającego oraz wymiennej pary gniazdo-trzpień ścinający (5, 4).

4-3c

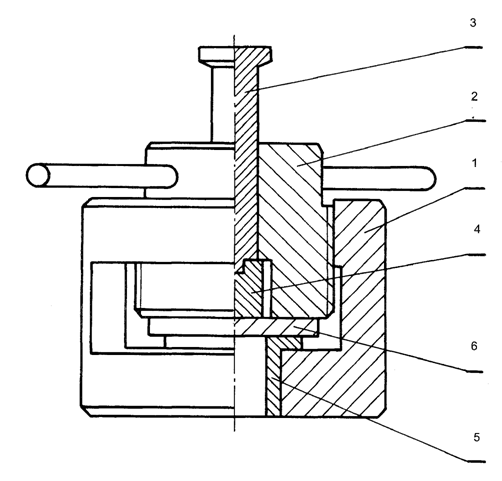
Rys. 4.3. Przyrząd do ścinania technologicznego

W korpusie osadzone jest wymienne gniazdo (5) o średnicy odpowiadającej średnicy trzpienia ścinającego (4). Próbka (6) umieszczana jest pomiędzy gniazdem i trzpieniem i przytrzymywana wkręcaną w korpus tuleją (2). W osi tulei jest pręt (3), który przenosi siłę obciążającą z prasy w trzpień ścinający

4. Plan ćwiczenia

Ćwiczenie polega na cylindrycznym ścięciu ośmiu próbek w przystosowanym do tego przyrządzie i wyznaczeniu doraźnej wytrzymałości na ścinanie technologiczne.

5. Tok przeprowadzenia ćwiczenia

1. Przygotuj osiem próbek, zmierz ich grubości z dokładnością 0,1 mm.

2. Zmierz średnice czterech sworzni ścinających z dokładnością 0,1 mm.

3. Każdym sworzniem zetnij dwie próbki i odczytaj maksymalne siły otrzymane przy ścinaniu. Podczas prób – obciążenia zwiększaj powoli, aby nie dopuścić do ścięcia dynamicznego.

6. Opracowanie wyników

Wpisz wyniki pomiarów i obliczeń w tabeli 4.1.

Tabela 4.1. Wyniki badań ścinania

Lp.

Grubość próbki

g [mm]

Średnica sworznia

d [mm]

Powierzchnia ścinana

S [mm²]

Największa siła

P [N]

Wytrzymałość na ścinanie

R₂ [N/mm² = MPa]

Wykonane pomiary ścinania i wpisane wartości liczbowe do tabeli 4.1, służą do oceny odporności badanego materiału na naprężenia styczne ścinające. Należy zwrócić szczególną uwagę na właściwe określenie powierzchni ścinania S badanej próbki, gdyż nagminnie popełniany jest błąd w jej wyznaczaniu. Do obliczenia powierzchni ścinania S, stosujemy wzór (4.2).

Pytania

1. Czym różni się ścinanie technologiczne od ścinania czystego?

2. Jaką figurą geometryczną jest powierzchnia ścinania?

Spis treści

Powrót do początku ćwiczenia

Ćwiczenie 5. Próba statyczna ściskania sprężyn śrubowych

1. Cel ćwiczenia

Zdjęcie charakterystyk λ = f(P) dwóch sprężyn pracujących:

a) pojedynczo (każda oddzielnie) – rys. 5.3a;

b) równolegle – rys. 5.3b;

c) szeregowo – rys. 5.3c.

Wyznaczenie dla każdej ze sprężyn:

a) modułu sprężystości postaciowej (G),

b) stałej sprężyny (c).

Obliczenie stałej (c) dla układu sprężyn połączonych:

a) równolegle,

b) szeregowo.

Przedmiotem badań będą sprężyny śrubowe walcowe wykonane z drutu, o przekroju kołowym (rys. 5.1).

5-1a

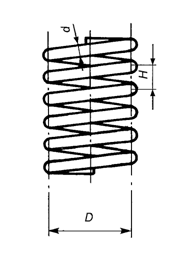
Rys. 5.1. Schemat sprężyny śrubowej walcowej wykonanej z drutu o przekroju kołowym: d – średnica drutu sprężyny, D – średnica sprężyny, H – skok sprężyny

Zależność skrócenia sprężyny (λ) od siły ściskającej (P) można przedstawiać w ten sposób (rys. 5.2), że skrócenie sprężyny jest wprost proporcjonalne do działającej siły (P)

gdzie współczynnik proporcjonalności (c) zwany jest stałą sprężyny

gdzie:

G – moduł sprężystości postaciowej materiału sprężyny,

d – średnica drutu sprężyny,

n – liczba zwojów sprężyny,

D – średnica sprężyny.

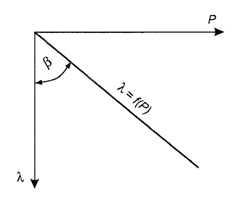
Rys. 5.2. Wykres charakterystyki sprężyny λ = f(P)

Aby wyznaczyć moduł sprężystości postaciowej (G) do równania (5.1) podstawiamy za (c) wyrażenie (5.2); otrzymamy wtedy równanie

Znając wartość siły (P), przy której nastąpiło maksymalne skrócenie sprężyny oraz wartość tego skrócenia (λ), z równania (5.3) wyznaczamy moduł (G)

Stałą sprężyny wyznaczamy z równania (5.1)

Układ sprężyn ściskanych w maszynie wytrzymałościowej pokazuje rysunek 5.3.

5-3c

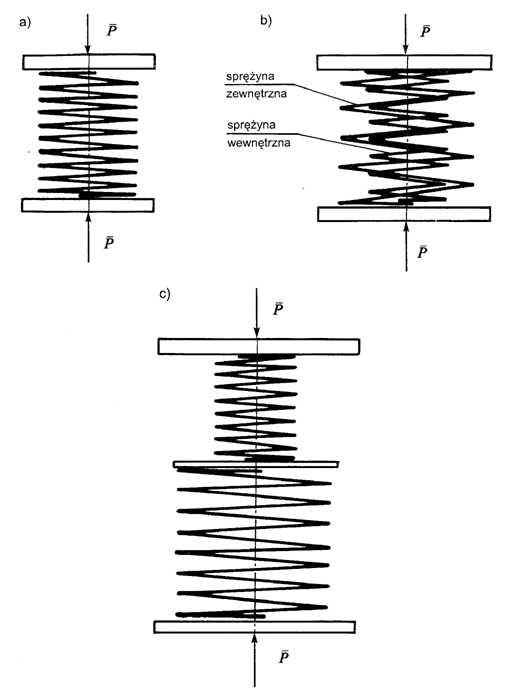
Rys. 5.3. Ściskanie sprężyn w maszynie wytrzymałościowej: a) pojedynczo, b) w układzie równoległym, c) w układzie szeregowym

Jeżeli mamy układ dwóch sprężyn połączonych równolegle to:

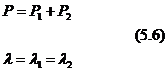
natomiast dla układu dwóch sprężyn połączonych szeregowo:

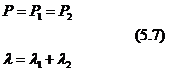
gdzie:

P – siła dla całego układu,

P_i – siła w i-tej sprężynie (i = 1, 2),

λ – odkształcenie układu,

λ_i – odkształcenie i-tej sprężyny (i = 1, 2),

Uwzględniając w układzie równań (5.6) i (5.7) równanie (5.1) otrzymujemy z układu równań (5.6):

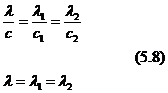
stąd stała układu dwóch sprężyn połączonych równolegle

z układu równań (5.7):

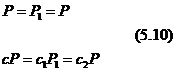
stąd stała układu dwóch sprężyn połączonych szeregowo

gdzie:

c_i – stała i-tej sprężyny

2. Aparatura pomiarowa

Do zdjęcia charakterystyk λ = f(P) wykorzystujemy maszynę wytrzymałościową, której schemat przedstawiony jest na rysunku 5.4. Silnik (1) wraz z układem przekładni pozwala na szybkie ustawienie na odpowiednim poziomie górnej płyty oporowej (2) maszyny. Dolna płyta (3), na której ustawiamy sprężynę (4), jest nieruchoma. Po ustawieniu górnej płyty i założeniu sprężyny ponownie uruchamiamy silnik. Górna płyta przemieszcza się w dół wywierając coraz większy nacisk na sprężynę. Wartość siły ściskającej wskazywana jest przez wskazówkę (7) siłomierza (6). Graficzny obraz zależności skrócenia sprężyny od działającej siły, wykreśla pisak (8) urządzenia samopiszącego (9). Otrzymany wykres to charakterystyka ściskanej sprężyny λ = f(P).

5-4c

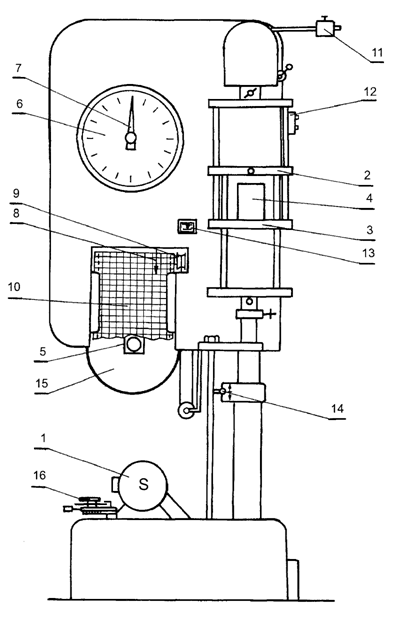
Rys. 5.4. Schemat maszyny wytrzymałościowej o napędzie mechanicznym: l – silnik wraz z układem przekładni, 2 – górna płyta oporowa maszyny, 3 – dolna płyta oporowa maszyny, 4 – badana sprężyna, 5 – wahadło siłomierza (6), 6 – siłomierz, 7 – wskazówka siłomierza, 8 – pisak urządzenia samopiszącego (9), 10 – bęben z nawiniętym papierem perforacyjnym, 11 – mechanizm do zerowania wskazówki siłomierza (6), 12 – listwa sterownicza, 13 – wskaźnik przemieszczeń płyty oporowej (2), 14 – ręczny przełącznik kierunku posuwu płyty oporowej (2), 15 – ciężarek wahadła (5), 16 – regulacja prędkości posuwu płyty oporowej (2)

3. Tok przeprowadzenia ćwiczenia

1. Określ dla każdej sprężyny wielkości (D, d, n).

2. Przeprowadź cztery próby ściskania:

a) sprężyny 1,

b) sprężyny 2,

c) obu sprężyn w układzie równoległym,

d) obu sprężyn w układzie szeregowym.

Próby przeprowadzaj jedynie do chwili, kiedy masz do czynienia ze ściskaniem, a nie zgniataniem sprężyn. W chwili kiedy zaczyna następować przyrost siły bez jednoczesnego przyrostu skrócenia sprężyny – przerwij doświadczenie (zaczyna się proces zgniatania sprężyny!) i odczytaj wartość siły (P_max) odpowiadającą maksymalnemu skróceniu sprężyny (λ_max).

4. Opracowanie wyników

Sprawozdanie z ćwiczenia powinno zawierać:

– opisane wykresy otrzymane z maszyny wytrzymałościowej (naniesiony układ współ- rzędnych, zaznaczone wartości maksymalne, siły (P) i skrócenia sprężyny (λ);

– graficzną interpretację stałych (c₁, c₂, c_r, c_sz);

– interpretację punktu, w którym następuje zmiana kąta nachylenia prostej λ = f(P) do osi poziomej na wykresie otrzymywanym w próbie (d);

– wypełnione tabele 5.1, 5.2, 5.3,

– wnioski i uwagi z przeprowadzonego ćwiczenia.

Tabela 5.1

D₁	[mm]
D₂	[mm]
d₁	[mm]
d₂	[mm]
n₁
n₂

gdzie indeksy 1, 2 oznaczają sprężynę 1 i sprężynę 2.

Tabela 5.2

Przeprowadzona próba	λ_max	P_max
Przeprowadzona próba	[mm]	[N]
ściskanie sprężyny 1
ściskanie sprężyny 2
ściskanie sprężyn połączonych równolegle
ściskanie sprężyn połączonych szeregowo

Tabela 5.3

G₁	[MPa]
G₂	[MPa]
c₁
c₂
c_r
c_sz

Pytania

1. Wyprowadź stałe układu (n) – sprężyn połączonych równolegle i szeregowo.

2. Określ stan naprężenia w sprężynie ściskanej pionową siłą (P).

Spis treści

Powrót do początku ćwiczenia

Ćwiczenie 6. Próba statyczna zginania

1. Cel ćwiczenia

Celem ćwiczenia jest praktyczne zapoznanie studenta ze sposobem przeprowadzenia próby statycznej zginania oraz ocena charakteru wykresu zginania, wyznaczenie sprężystości podłużnej (E) badanego materiału.

Próba zginania należy do często stosowanych prób wytrzymałościowych. Nadaje się w szczególności do określania własności mechanicznych materiałów konstrukcyjnych kruchych, których własności próba rozciągania w pełni nie odzwierciedliła. Próba zginania polega na zmianie pierwotnej krzywizny osi podłużnej belki pod wpływem układu sił prostopadłych do tej osi, działających w płaszczyźnie przechodzącej przez oś belki (rys. 6.1).

6-1c

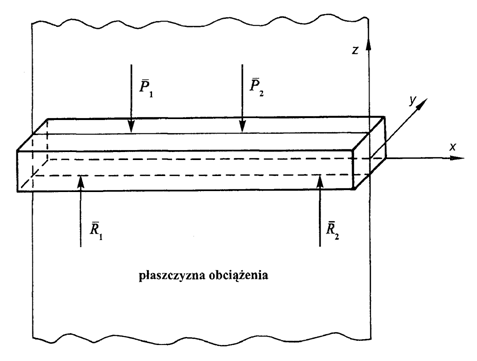
Rys. 6.1. Zginanie proste

Jeżeli płaszczyzna obciążenia przechodzi także przez jedną z głównych centralnych osi bezwładności przekroju poprzecznego – mówimy o zginaniu prostym, jeżeli nie przechodzi – to o zginaniu ukośnym.

Na przekrój poprzeczny belki zginanej działa moment zginający (M_g) i siła poprzeczna (T). Moment zginający jest równoważony w przekroju przez układ naprężeń normalnych, natomiast siłę poprzeczną równoważy wypadkowa naprężeń stycznych, działających w płaszczyźnie przekroju.

Naprężenia styczne można wyeliminować odpowiednio dobierając układ sił zewnętrznych, przy których siła tnąca w pewnej części belki jest równa zeru. Taki przypadek zginania nazywamy zginaniem czystym. W praktyce inżynierskiej ze zginaniem czystym spotykamy się bardzo rzadko.

Próbę zginania przeprowadzić należy według jednego z dwóch schematów obciążenia przedstawionych na rysunkach (6.2) i (6.3).

1. Obciążenie siłą (P) w środku belki i siłami (P/2) od podpór na jej końcach (rys. 6.2).

W tym przypadku największy moment zginający wynosi

Największe naprężenie normalne pochodzące od momentu M_g wynosi

Ugięcie belki w miejscu przyłożenia siły (P) określa wzór

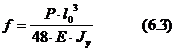
Wytrzymałość na zginanie

gdzie:

P_kr – siła krytyczna niszcząca próbkę. W przypadkach wątpliwych największa siła – obciążająca próbkę,

J– moment bezwładności przekroju,

W_g – wskaźnik wytrzymałości przekroju przy zginaniu,

l₀ – jak na schemacie (rys. 6.2).

2. Obciążenie symetryczne, dwiema siłami (P/2) pomiędzy podporami (rys. 6.3). Największy moment zginający dla tego przypadku wynosi

Największe naprężenie normalne od tego momentu

6-2c

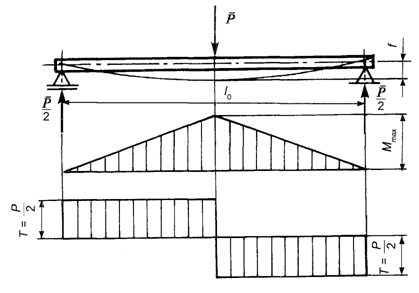
Rys. 6.2. Schemat 1 zginania próbki obciążonej siłą (P) w środku

6-3c

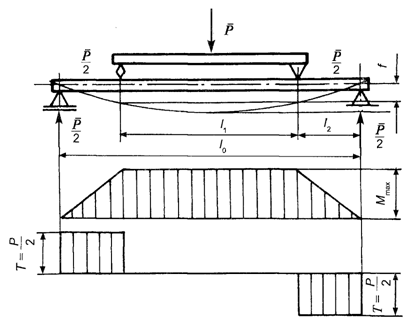
Rys. 6.3. Schemat 2 zginania próbki obciążonej dwiema siłami (P/2)

Ugięcie belki w miejscu przyłożenia sił (P/2)

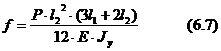
Wytrzymałość na zginanie

l₁, l₂ – jak na schemacie obciążenia (z rys. 6.3).

Wyżej przedstawione wzory wyprowadza się przy pewnych założeniach:

– materiał zachowuje się zgodnie z prawem Hooke’a;

– oś obojętna przechodzi przez środek ciężkości przekroju, tj. materiał zachowuje się symetrycznie przy rozciąganiu i ściskaniu;

– przy wyprowadzaniu równania różniczkowego linii ugięcia belki zakłada się tylko czyste zginanie.

W obliczeniach wytrzymałościowych powszechnie stosuje się wzory oparte na tych założeniach, mimo iż rzadko są one w praktyce spełnione. Znane są bardziej ogólne opisy zginania nie wychodzące z tych założeń, lecz korzyści z ich praktycznego stosowania są na ogół małe w porównaniu z komplikacją obliczeń jaką powodują.

Wytrzymałość na zginanie jest wielkością umowną. Można ją traktować jako wielkość porównawczą dla oceny różnych materiałów.

2. Maszyna wytrzymałościowa

Do próby używa się maszyny wytrzymałościowej o napędzie mechanicznym, pokazanej na rysunku 6.4. Działanie i obsługę maszyny opisano w ćwiczeniu nr l.

3. Próbki

Podczas ćwiczenia stosowane są próbki o przekroju okrągłym lub prostokątnym. Materiał próbek może być różny. Wymiary próbek należy pomierzyć z dokładnością 0,1 mm, ugięcie próbek z dokładnością 0,5 mm, obciążenia z dokładnością jednej działki elementarnej na skali siłomierza.

4. Plan ćwiczenia

Przeprowadzić próbę zginania trzech próbek wg schematu obciążenia 1 lub 2. Na podstawie pomiarów siły niszczącej próbkę wyznaczyć wytrzymałość na zginanie (R_g). Porównując wzór teoretyczny na ugięcie belki z pomiarami wyznaczyć moduł sprężystości podłużnej (E). Oceń jaki charakter ma wykres zginania próbek i w jakim zakresie jest on liniowy.

6-4c

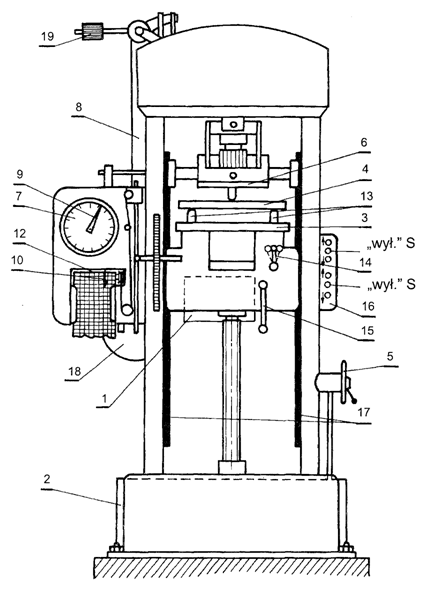
Rys. 6.4. Schemat maszyny wytrzymałościowej używanej w próbie zginania:

1 – silnik S1 (do szybkiego posuwu płyty oporowej (3)) wraz z przekładnią, 2 – silnik S2 z przekładnią, 3 – dolna płyta oporowa maszyny, 4 – badana próbka, 5 – regulacja prędkości posuwu płyty oporowej (3), 6 – górna płyta oporowa maszyny, 7 – siłomierz, 8 – wahadło siłomierza, 9 – wskazówka siłomierza, 10 – pisak urządzenia samopiszącego (11), 12 – bęben z nawiniętym papierem perforacyjnym, 13 – podpory, 14 – przełącznik (napęd mechaniczny – napęd ręczny), 15 – korba napędu ręcznego, 16 – listwa sterownicza, 17 – prowadniki płyt oporowych (3) i (6), 18 – ciężarek wahadła (8), 19 – mechanizm do zerowania wskazówki siłomierza (7)

5. Tok przeprowadzenia ćwiczenia

a) Zamontuj na maszynie wytrzymałościowej podpory realizujące wybrany schemat obciążenia. Zmierz odległości (l₀, l₁, l₂) pomiędzy podporami.

b) Zmierz wymiary próbki, umieść ją w maszynie. Obciąż wstępnie próbkę dla wyeliminowania luzów. Siłomierz powinien wskazywać zero lub nieznacznie więcej.

c) Ustal i zanotuj położenie początkowe znacznika na listwie pomiarowej (l_p). Przygotuj rejestrator.

d) Obciążaj próbkę na napędzie ręcznym aż do zniszczenia. Jeżeli wskazania siłomierza zaczynają wyraźnie spadać, przyjmij, że próbka jest zniszczona, a największa siła jest krytyczną siłą niszczącą (P_kr).

e) Odczytaj siłę (P_kr). Zanotuj w tabeli 6.1 odpowiadające tej sile, końcowe położenie znacznika na listwie pomiarowej (l_k). Przemieszczenie znacznika względem listwy jest równe ugięciu belki w punkcie przyłożenia siły.

f) Powtórz próbę dla dwóch pozostałych próbek według punktów od 2 do 5.

6. Pomiary

Materiał próbek . . . . . . . . . . . . . . . . . . . .

Tabela 6.1

Lp.	Wymiary przekroju d lub a i b [mm]	Ugięcie			P_kr [N]	R_g [MPa]	E [MPa]
Lp.	Wymiary przekroju d lub a i b [mm]	l_p [mm]	l_k [mm]	f = (l_p – l_k) [mm]	P_kr [N]	R_g [MPa]	E [MPa]
1
2
3

7. Opracowanie wyników

a) Opisz charakter otrzymanych wykresów zginania.

b) Oblicz (R_g) i (E) jako średnie arytmetyczne z trzech prób.

c) Przedstaw swoje wnioski i uwagi na temat ćwiczenia. Przeprowadź dyskusję na temat otrzymanych wyników. Porównaj otrzymane wyniki z wartościami tablicowymi. Jeżeli to możliwe, porównaj wartości modułu Younga wyznaczone na podstawie próby zginania i na podstawie próby rozciągania.

Pytania

1. Narysuj wykresy momentów i sił tnących dla schematów obciążenia z rysunków 6.2 i 6.3.

2. Podaj szkic wyprowadzeń wzorów, które wykorzystywałeś do obliczenia wytrzymałości na zginanie i ugięcia. Gdzie pojawiają się założenia, które wymieniono wcześniej.

3. Czy w sposobie przeprowadzenia ćwiczenia znajdujesz źródła dodatkowych błędów wpływających na rezultaty?

Spis treści

Powrót do początku ćwiczenia

Normy

PN80/H-04310. Próba statyczna rozciągania metali

PN77/H-04307. Metale niezależne. Pobieranie i przygotowanie próbek do próby rozciągania

PN84/H-04308. Stal. Pobieranie próbek do badań własności mechanicznych

PN84/B-04110. Oznaczenie wytrzymałości na ściskanie materiałów kamiennych

PN86/H-04321. Metale. Próba ścinania

BN75/8704-08. Skały zwięzłe. Oznaczenie wytrzymałości na ścinanie

Zalecenia normalizacyjne CSRS – PRL – PCS. Oznaczanie wytrzymałości na rozciąganie metodą poprzecznego ściskania

PN80/H-83119. Próba statyczna ściskania żeliwa szarego

Powrót do początku