III. DYNAMIKA

7. Dynamika ruchu postępowego

Mechanika klasyczna opiera się na trzech podstawowych prawach noszących nazwę zasad dynamiki Newtona.

Przykładowe sformułowania tych zasad:

I. Istnieje taki układ odniesienia, w którym, jeżeli na ciało nie działa żadna siła lub siły działające na to ciało równoważą się, to ciało zachowuje stan spoczynku lub porusza się ruchem jednostajnym po linii prostej.

Układy odniesienia, o których mówi I zasada noszą nazwę układów inercjalnych.

II. Jeżeli na ciało o masie m działają siły o wypadkowej , to ciało porusza się ruchem przyspieszonym z przyśpieszeniem takim, że

(7.1)

W/w zasady mówią o jednym ciele, jednak w zadaniach zwykle mamy do czynienia z układami co najmniej dwóch ciał działających nawzajem na siebie i wtedy stosujemy III zasadę:

III. Jeżeli na ciało A działa na ciało B siłą , to ciało B oddziałuje na ciało A taką samą co do wartości siłą , lecz skierowaną przeciwnie.

Siły te są jednakowe co do wartości i skierowane przeciwnie, lecz nie znoszą się ani nie równoważą, gdyż są przyłożone do różnych ciał.

Wskazówka:

Przy rozwiązywaniu zadań z dynamiki zwracamy uwagę na kolejność czynności tj. :

1. wykonujemy rysunek, wyraźnie zaznaczając odrębność ciał tworzących układ;

2. badamy, jakie siły działają na poszczególne ciała tworzące siły i rysujemy te siły;

3. przyjmujemy układ odniesienia, w którym będziemy zapisywać równania ruchu: wybór uzależniamy od treści zadania;

4. zapisujemy dla każdego ciała osobno równanie II zasady dynamiki.

Przykład:

Kontener na wadze elektronicznej przedstawione są na rysunku 7.1:

Kontener A i wagę B traktujemy jako dwa odrębne ciała. Analizujemy jakie siły działają na ciała i gdzie są one przyłożone:

1. w środku masy ciała A przyłożona jest siła ciężkości m

2. siła m dociska ciało A do ciała B, a więc ciało A działa na ciało b siłą ; siła ta jest przyłożona do wagi (rys 7.1). Zauważamy, że co do wartości mg = N_AB.

3. zgodnie z III zasadą dynamiki ciało B oddziałuje na A siłą . Siła ta jest przyłożona do kontenera (rys.7.1). Co do wartości siły N_AB i N_BA są takie same.

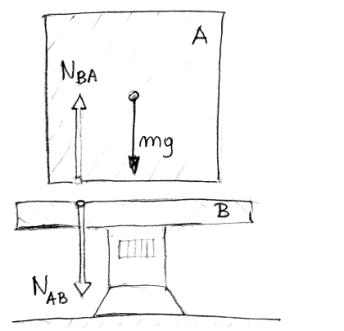
Rys.7.1. Kontener spoczywający na wadze – u kład sił

Skutki działania sił:

Z powyższej analizy wynika, że wartości sił są takie same, tzn mg=N_AB=N_BA.

Natomiast wektory sił i leżą na tym samym kierunku i są przeciwnie skierowane, a ponieważ zaczepione są to tego samego ciała A, w rezultacie równoważą się i kontener pozostaje w spoczynku. Siła oddziałuje z sensorem wagi, która wskazuje wynik ważenia.

W większości zadań z dynamiki występujące w nich siły można sprowadzić do sił grawitacji, sił sprężystego oddziaływania i sił tarcia. W wielu zadaniach ciała oddziałują ze sobą za pośrednictwem sprzęgów (nici, liny) i wtedy występują siły naciągu np. liny.

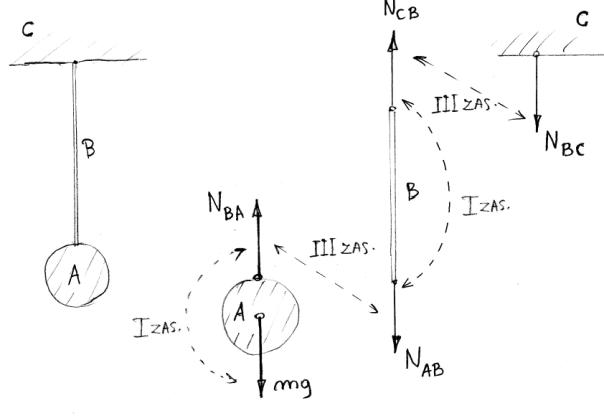
Rys.7.2. Przenoszenie sił poprzez sprzęgi, nitki, liny

Przykład:

Na rysunku 7.2 przedstawiono lampę (A) na sznurze(B) przymocowaną do stropu(C).

1. Na lampę A działa siła przyciągania ziemskiego mg i równoważąca ją siła przyłożona od strony sznura do lampy. Siły te są sobie równe, przeciwnie skierowane, a ponieważ są przyłożone do tego samego ciała, więc się równoważą (mg=N_BA) i lampa pozostaje w spoczynku (I zas.)

2. Lampa –sznur; Sznur działa na lampę siłą skierowaną do góry. Jak wynika z III zasady, od strony lampy na sznur działa siła ,. Jednocześnie wartości tych sił są takie same, a zwroty skierowane przeciwnie (rys). Siły te nie mogą się znosić, ponieważ przyłożone są do różnych ciał!

3. Sznur; Na sznur działa siła od strony lampy i taka sama co do wartości, ale skierowana przeciwnie, przyłożona od strony stropu siła . Siły te równoważą się ponieważ przyłożone są do tego samego ciała i sznur pozostaje w spoczynku (I zas.)

Wartość N_AB=N_AC nazywamy naciągiem (napięciem) sznura

4. Sznur-strop. Strop działa na sznur siłą , a sznur na strop zgodnie z III zasadą siłą . Więc siły te mają taką samą wartość, są przeciwnie skierowane lecz nie znoszą się, bo działają na różne ciała.

Analiza sił tarcia posuwistego

Zapamiętajmy:

Siła tarcia działa na ciało zawsze w płaszczyźnie styku z powierzchnią, po której ciało się posuwa i jest zawsze skierowana przeciwnie do ruchu części trących. Zgodnie z III zasadą; na podłoże po którym porusza się ciało, działa siła . Wartości tych sił są takie same, siły te mają przeciwne zwroty, ale nie znoszą się i nie równoważą bo są przyłożone do różnych ciał (patrz rysunek 7.3).

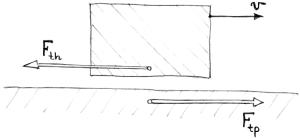
Rys.7.3. Siła tarcia

W zadaniach przyjmujemy, że wartość siły tarcia posuwistego zależy od współczynnika tarcia m , charakteryzującego powierzchnie trące, oraz od nacisku . Nacisk określamy jako siłę, lub składową od innych sił, prostopadle przyciskającą ciało do powierzchni, po której się porusza. Wartość siły tarcia wynosi wtedy .

Przykłady:

1. Przedstawienie graficzne sił występujących w trakcie zsuwania i klocka pod wpływem siły ciężkości po bieżni pochylonej pod kątem a.

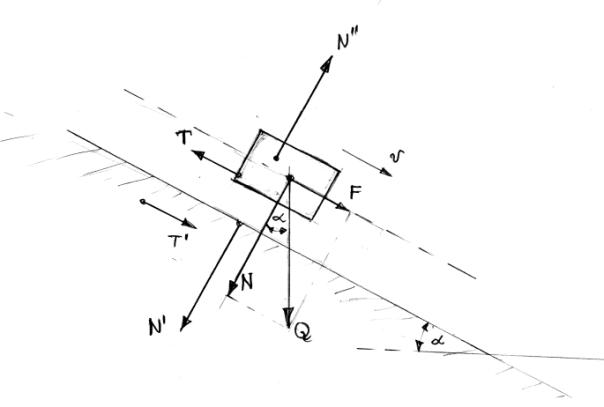
Rys.7.4. Układ sił na równi pochyłej

2. Działanie sił tarcia w trakcie ruchu samochodu posiadającego napęd na oś przednią.

Rys.7.5. Siły tarcia podczas ruchu samochodu

W prawidłowym analizowaniu sił i zapisywaniu równań ruchu pomaga stosowanie następujących pojęć fizycznych:

- Układ ciał

Układem ciał w fizyce nazywamy zbiór ciał, myślowo wyodrębniony od otoczenia

Jeżeli ciała stanowiące otoczenie nie wywierają sił na w/w zbiór ciał tzn. układ (albo gdy działania zewnętrznych ciał się znoszą), uważamy wtedy, że układ jest izolowany lub – odosobniony.

- Siły zewnętrzne

Siłami zewnętrznymi nazywamy te siły, które działają na układ z zewnątrz, tzn. od strony ciał nie należących do układu.

- Siły wewnętrzne

Siłami wewnętrznymi nazywamy te siły, które działają między ciałami tworzącymi układ

Zapamiętajmy:

Dynamiczne równania ruchu opisujące rozważany problem uzyskuje się poprzez znalezienie wszystkich sił działających na poszczególne ciała (masy) występujące w zadaniu i zapisując relacje wynikające z II zasady dla poszczególnych ciał (mas). Uzyskujemy wtedy układ równań rozwiązanie którego daje oczekiwany wynik.

8. Dynamika w nieinercjalnych układach odniesienia

Zapamiętajmy:

Nieinercjalny układ odniesienia przemieszcza się z przyśpieszeniem.

Obserwator związany z nieinercjalnym układem odniesienia nie może do opisu zachowania się ciał zastosować I zasady dynamiki.

Aby wytłumaczyć zachowanie się ciał w tym układzie za pomocą zasad dynamiki, obserwator musi wprowadzić siłę pozorną, tzw. siłę bezwładności , która jest skierowana przeciwnie niż przyśpieszenie układu. Siła ta istnieje tylko w układzie nieinercjalnym i nadaje ciału w tym układzie przyspieszenie . Tzn. , gdzie jest przyspieszeniem układu.

Wskazówka:

Należy zwrócić uwagę na istotne zjawisko, mianowicie, że pozorna siła bezwładności jest zawsze skierowana przeciwnie skierowana do przyśpieszenia (opóźnienia) układu odniesienia, a nie zależy od tego, w którą stronę układ się porusza.

Przykład:

Na wadze elektronicznej, znajdującej się w windzie położono ciało o masie m. Jakie będą wskazania wagi, jeżeli winda jedzie z przyspieszeniem a do góry:

a. Jak uzasadni odpowiedzi obserwator A przebywający w inercjalnym układzie odniesienia,

b. obserwator B znajdujący się w windzie ( w nieinercjalnym układzie odniesienia)

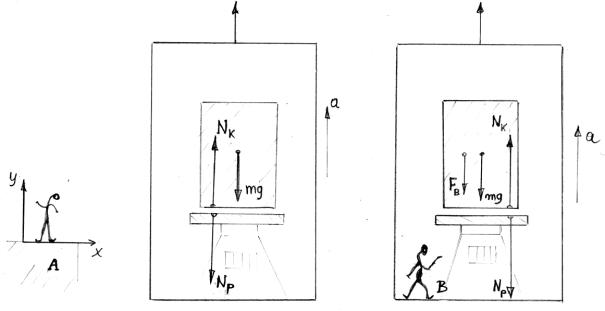
Rys.8.1. Winda – układ inercjalny i nieinercjalny

Obserwator A,

Związany z układem inercjalnym (XY – rysunek 8.1 ) spostrzega, że na ciało działają:

- siła ciężkości skierowana w dół,

- siła przyłożona od strony szalki wagi,

na szalkę działa siła . rejestrowana przez sensor wagi. Jednocześnie co do wartości

N_K=Np (8.1)

Obserwator A układa równania (II zasada) dla masy m, która porusza się z przyśpieszeniem a;

N_K – mg = ma (8.2)

N_K = m(g + a) (8.3)

Więc wskazanie wagi wynosi:

N_P = N_K = m(g + a) (8.4)

Obserwator B,

Związany z układem nieinercjalnym (winda porusza się z przyśpieszeniem a ) uwzględnia działanie siły bezwładności na masę m, a ponieważ masa m jest względem niego w spoczynku pisze równania równowagi sił pamiętając, że (skierowana przeciwnie do przyspieszenia windy):

N_K = mg + ma

Wskazanie wagi wynosi

N_P = N_K = m(g + a)

Jak widać, w obu przypadkach obserwatorzy wykonają identyczny pomiar.

Literatura:

[1] M.A.Herman, A.Kalestyński, L.Widomski, Podstawy fizyki dla kandydatów na wyższe uczelnie i studentów, PWN Warszawa 1999

[2] D.Halliday, R.Resnick, J.Wlker, Podstawy Fizyki tom 1, PWN, Warszawa 2005