11. DYNAMIKA RUCHU DRGAJĄCEGO

Ruchem drgającym nazywamy ruch, który powtarza się periodycznie w trakcie jego trwania w czasie i zachodzi wokół położenia równowagi. Zespół obiektów fizycznych zapewniający wytworzenie ruchu drgającego nazywamy układem drgającym.

W każdym układzie drgającym, aby układ mógł wykonywać drgania musi być spełniony podstawowy warunek polegający na tym, że każdemu wychyleniu układu z położenia równowagi musi towarzyszyć siła skierowana przeciwnie do wychylenia, tzn. skierowana w stronę położenia równowagi. Siłę tę nazywamy kierującą lub zawracającą.

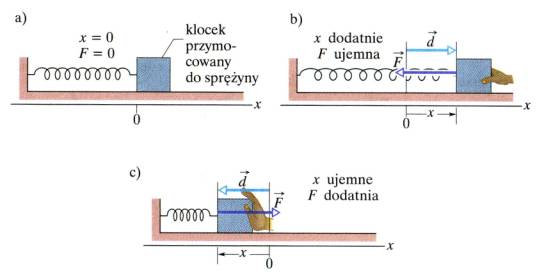
Rys. 11.1. a) Sprężyna nieodkształcona. Jak początek osi X przybieramy położenie tego końca sprężyny, do którego położony jest klocek. b) Przemieszczamy klocek o d przy czym sprężyna zostaje rozciągnięta w kierunku dodatnich x. Zwrócić uwagę na siłę zwrotną działającą na klocek. c) Sprężyna zostaje ściśnięta – zwrócić uwagę na siłę zwrotną.

Energia w ruchu drgającym

Jednowymiarowy ruch drgający powodowany jest siłą:

Praca tej siły na drodze x wynosi

a po zróżniczkowaniu

Całkowanie graficzne sprowadza się do policzenia pola powierzchni pod krzywą – rys. 11.2

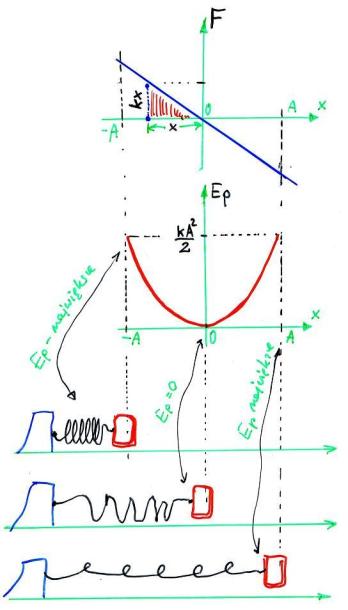
Rys. 11.2. Zależność siły od wychylenia, praca jako całka (pole zakreskowanego trójkąta) , wykres energii potencjalnej w funkcji położenia ciała.

Energia potencjalna (analitycznie)

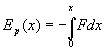
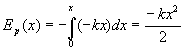
Czasowe przebiegi parametrów ruchu i energii w ruchu drgającym

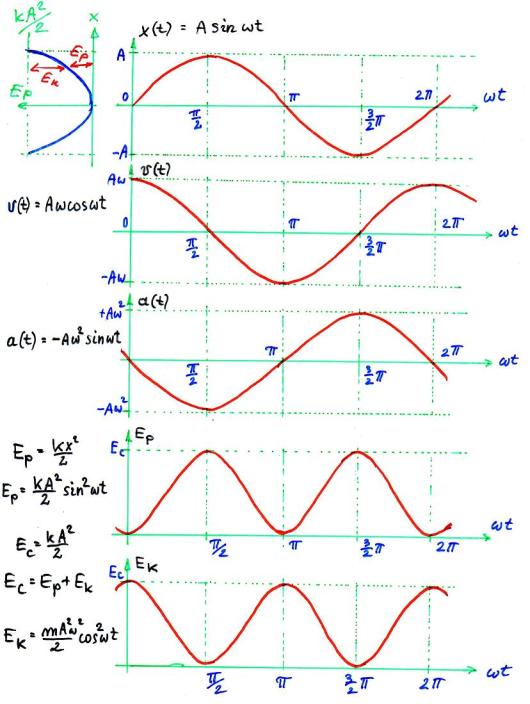
Rys. 11.3. Czasowe przebiegi położenia, prędkości i przyspieszenia punktu materialnego w ruchu drgającym. Energia potencjalna i energia kinetyczna.

12. Dynamika ruch po torach kołowych

W zjawiskach przyrodniczych i urządzeniach technicznych bardzo często spotykamy się z ruchem obrotowym.

Określenia:

Ciało sztywne – to ciało, które porusza się w taki sposób, że wszystkie jego części są związane ze sobą dzięki czemu kształt ciała nie ulega zmianie.

Stała oś – obrót zachodzi wokół osi, której położenie nie zmienia się w czasie ruchu ciała, i tę oś nazywamy osią obrotu.

Ruch obrotowy – Każdy punkt ciała sztywnego porusza się po okręgu, którego środek leży na osi obrotu i każdy punkt zakreśla w ustalonym czasie taki sam kąt.

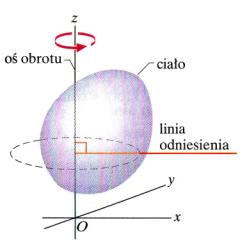
Rys. 12.1. Ciało sztywne o dowolnym kształcie obracające się wokół osi z układu współrzędnych. Linia odniesienia została wybrana w obrębie ciała dowolnie, z tym że prostopadła do osi obrotu. Jest ona związana z ciałem i obraca się razem z nim.

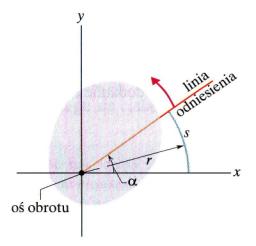
Rys. 12.2. Przekrój płaszczyzną xy obracającego się ciała w rysunku 12.1 (czyli jego widok z góry). Płaszczyzna przekroju jest prostopadła do osi obrotu, która jest teraz skierowana prostopadle go kartki, w kierunku patrzącego. Położenie ciała jest określone przez kąt a jaki tworzy linia odniesienia z osią x.

(12.1)

1 pełny obrót = 360°=rad (12.2)

1 rad = 57,3°=0,159 pełnego obrotu (12.3)

Położenie kątowe – kąt jaki tworzy linia odniesienia z pewnym stałym kierunkiem, wybranym za kierunek o zerowym położeniu kątowym

Przemieszczenie kątowe -

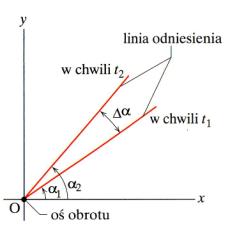
Rys. 12.3. Linia odniesienia ciała sztywnego z rysunków 12.1 i 12.2 ma w chwili t₁ położenie kątowe a₁, a w pewnej późniejszej chwili t₂ położenie kątowe a₂. Wielkość Da=a₂-a₁ jest przemieszczeniem kątowym ciała w czasie Dt=t₂-t₁. Samo ciało sztywne nie zostało ty narysowane.

Zapamiętajmy:

Przemieszczenie kątowe jest dodatnie, jeśli obrót zachodzi w kierunku przeciwnym do kierunku wskazówek zegara, a jest ujemne , jeśli zachodzi w kierunku zgodnym z kierunkiem wskazówek zegara.

Związek zmiennych liniowych z kątowymi

Między kinematycznymi wielkościami kątowymi i liniowymi istanieją proste związki matematyczne. Wyprowadzimy je korzystając ze znanej z geometrii elementarnej zależności między wartością kąta środkowego Da a długością łuku Ds okręgu o promieniu r, na którym ten okrąg jest oparty,

(12.4)

Wychodząc z definicji prędkości kątowej

(12.5)

Po podstawieniu zależności 12.4 do 12.5 otrzymujemy

(12.6)

Analogiczny związek istnieje między wartościami średnimi tych prędkości

(12.7)

oraz pomiędzy przyrostami tych prędkości

(12.8)

Wychodząc następnie z definicji przyspieszenia kątowego

(12.9)

a następnie podstawiając zależność 12.8 otrzymamy

(12.10)

Zależności między wektorami kinematycznych wielkości kątowych i liniowych można wyrazić za pomocą następujących iloczynów wektorowych

(12.11)

(12.12)

(12.13)

Usytuowanie przestrzenne wektorów występujących w ostatnich wzorach pokazano na rysunku 12.4

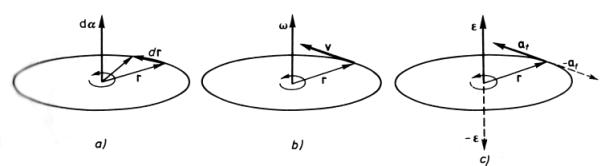
Rys. 12.4. Usytuowanie przestrzenne wektorów kinematycznych wielkości kątowych i liniowych

13. Ruch falowy

Równanie fali sinusoidalnej

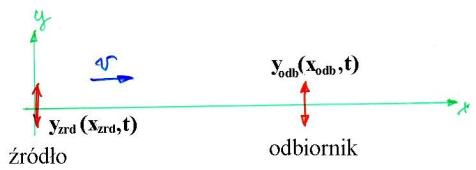
Rys. 13.1. Rozchodzenie się zaburzenia sinusoidalnego (poprzecznego) wzdłuż osi x z prędkością v.

Drgania punktu źródłowego opisuje równanie

Dla punktu nazwanego odbiornik

gdzie

tak wiec w odbiorniku mamy

Dla dowolnego x mamy

V – prędkość rozchodzenia się fali

Y – amplituda drgań

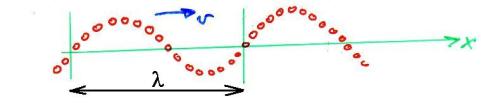
Rys. 13.2. „fotografia” drgających punktów uczestniczących w ruchu falowym (obserwujemy wszystkie w tym samym czasie)

Na rysunku zaznaczono długość fali czyli odległość pomiędzy dwoma punktami drgającymi w tej samej fazie – oznaczamy ją l. Ważną wielkością jest też okres (oznaczany przez T) – jest to czas w którym fala przebywa odległość równą długości fali. Okres jest też odwrotnością częstotliwości fali (oznaczaną f).

Równanie fali, liczba falowa

Wychodząc z równania fali

podstawiając

wielkość zwana jest liczbą falową

ostatecznie równanie fali sinusoidalnej zapisujemy w postaci

Równanie to obowiązuje zarówno dla fali poprzecznej jak i podłużnej.

Należy podkreślić że w ruchu falowym w kierunki propagacji fali (zaburzenia) mamy transport energii a nie masy.