3. Kinematyka – podstawowe pojęcia i wielkości

 

            Kinematyka zajmuje się opisem ruchu ciał. Ruch ciała opisujemy w ten sposób, że podajemy położenie tego ciała w każdej chwili względem wybranego układu współrzędnych. Poprawny opis ruchu wymaga zawsze podania układu odniesienia względem którego ten ruch jest opisywany.

 

3.1 Kartezjański układ współrzędnych

 

Rys.3.1. Kartezjański układ współrzędnych – przypadek 2 i 3 wymiarowy

 

3.2 Wektor położenia i wektor przemieszczenia

 

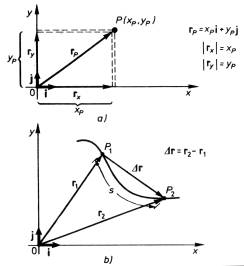
Rys.3.2.Wektor położenia i przemieszczenia

 

Uwaga: Przemieszczenia  jest wielkością wektorową.

 

3.3 Kinematyczne równanie ruchu

Kinematyczne równanie ruchu ciała jest to zależność (układ równań) podająca wartości współrzędnych ciała w funkcji czasu. W postaci wektorowej jest to zależność określająca wektor położenia ciała jako funkcję czasu.

                                                                                                                   (3.1)

Skalarna postać kinematycznego równania ruchu jest układem następujących zależności

 

                                                                                                                                (3.2)

                                                                                                                               (3.3)

                                                                                                                                (3.4)

 

3.4 Równanie toru ruchu

Eliminując czas z równania ruchu można otrzymać równanie toru ruchu. Np. na płaszczyźnie równanie toru jest funkcją jednej zmiennej.

                                                                                                                              (3.5)

3.5 Parametry kinematyczne ruchu

 

3.5.1 Prędkość średnia – jest to stosunek przemieszczenia ciała jakie dokonało się w pewnym czasie obserwacji do długości tego czasu

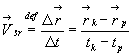                                                                                                            (3.6)

 

3.5.2 Prędkość chwilowa – określa sposób przemieszczania ciała w każdym momencie ruchu. Jest pierwszą pochodną przemieszczenia ciała względem czasu.

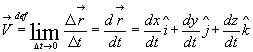                                                                              (3.7)

 

3.5.3 Przyspieszenie średnia – jest to stosunek zmiany prędkości jaki nastąpił w pewnym czasie do tego czasu.

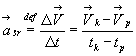                                                                                                           (3.8)

3.5.4 Przyspieszenie chwilowe – jest pochodną prędkości ciała względem czasu.

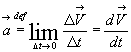                                                                                                            (3.9)

Warto zauważyć że wektor prędkości jest w czasie trwania ruchu zawsze styczny do krzywej toru. Inaczej jest z przyspieszeniem – jego wektor jest styczny do toru jedynie w ruchu prostoliniowym. W ruchu krzywoliniowym oprócz przyspieszenia stycznego występuje dodatkowo przyspieszenie normalne (prostopadłe do toru ruchu i odpowiedzialne za zmianę kierunku wektora prędkości). Całkowite przyspieszenie (wypadkowe) jest sumą geometryczną tych dwóch składowy (rys.3.3)

Rys.3.2.Przyspieszenie ciała w ruchu krzywoliniowym

4. Ruchy prostoliniowe

 

4.1 ruch prostoliniowy jednostajny

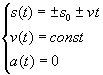                                                                                                        (4.1)

 

4.2 ruch prostoliniowy jednostajnie zmienny

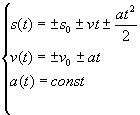                                                                                                          (4.2)

 

4.3 zasada składania ruchów

Każdy ruch można przedstawić jako złożenie ruchów składowych obserwowanych (rzutowanych) na osiach układu współrzędnych XYZ. Ruchy składowe wiąże ten sam czas !

 

 

5. Ruch po okręgu

Ciało poruszając się po okręgu cały czas zmienia kierunek wektora prędkości – ruch wiec jest ruchem zmiennym.

 

5.1 Ruch jednostajny po okręgu.

W tym ruchu wektor prędkości styczny do toru stale zmienia swój zwrot. W ruchu jednostajnym

                                                                                                                (5.1)

Y

Jest to ruch krzywoliniowy w którym występuje przyspieszenie normalne o wartości

                                                                                                                   ( 5.2 )

 

skierowane stale do środka okręgu o promieniu r, zwane przyspieszeniem dośrodkowym.

 

Wyprowadzenie wzoru 5.2. [2]

 

W celu wyznaczenia wartości i kierunku przyspieszenie w ruchu jednostajnym po okręgu przeanalizujemy rys. 5.1.

 

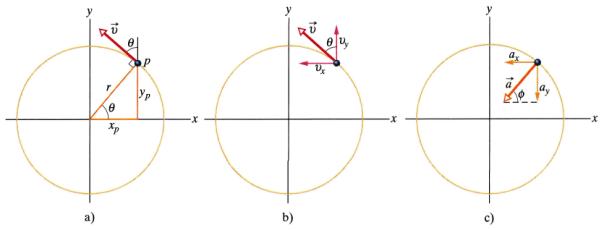Rys.5.1. Częstka p porusza się jednostajnie po okręgu w kierunku przeciwnym do ruchu wskazówek zegara: a) jej położenie i prędkość V w pewnej chwili; b) prędkość V i jej skłądowe; c) przyspieszenie a cząstki i jego składowe

 

Na rysunku 5.1a cząstka porusza się z prędkością V o stałej wartości po okręgu o promieniu r. W chwili, dla której wykonano ten rysunek współrzędne tej cząstki wynoszą xp i yp.

Wiedząc że prędkość jest zawsze styczna do toru ruchu. Jak to widać z rysunku 5.1a oznacza to ze w ruchu po okręgu prędkość jest zawsze prostopadła do promienia w punkcie w którym w danym momencie znajduje się cząstka. Kąt q, utworzony przez z pionem w punkcie p jest więc równy kątowi utworzonemu przez promień r z osią x.

Składowe wektora  pokazano na rysunku 4.19b. Korzystając z nich możemy zapisać prędkość  jako:

                                                                 (5.3)

Z trójkąta prostokątnego na rys. 5.1a widać, że , a  co daje:

                                                                                          (5.4)

Aby wyznaczyć przyspieszenie  cząstki p, należy zróżniczkować to równanie względem czasu. Wartość prędkości  oraz promienia r na zależą od czasu, otrzymujemy więc:

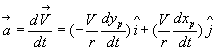                                                                           (5.5)

Można zauważyć, że szybkość zmiany yp, dyp/dt jest równa skłądowej prędkości Vy. Analogicznie dxp/dt = Vx. Z rysunku 5.1b widać, że , a . Podstawiając te związki do równania 5.5 otrzymujemy:

                                                                            (5.6)

Ten wektor oraz jego składowe pokazano na rys. 5.1c. W zgodzie z równaniem 5.2 otrzymujemy że długość wektora  jest równa:

                                                       (5.7)

no należało pokazać.

 

 

Ruch jednostajny po okręgu jest ruchem okresowym – co jakiś czas ciało przebiega przez ten sam punkt toru – jest to okres tego ruchu oznaczany jako T. Odwrotnością okresu jest częstotliwość

                                                                                                                      (3.14)

 

 

6.Kinematyka rzutów ukośnych i poziomych

Zależności kinematyczne występujące przy rzutach najwygodniej jest rozpatrywać korzystając z zasady niezależności ruchów. Możemy wtedy ruch ciała, np. przy rzucie ukośnym, zawsze rozłożyć na dwa ruchy składowe ruch ciała z prędkością początkową V0Yw kierunku pionowym z przyspieszeniem  g,  skierowanym ku ziemi oraz równoczesny ruch z prędkością V0X w kierunku poziomym.

Metodyka rozwiązywania zadań:

-         wprowadzamy układ odniesienia

-         rozkładamy prędkość V0 na składowe V0X i V0Y

-         korzystając z zasady niezależności ruchów zapisujemy równania ruchów składowych oddzielnie dla osi x i y. Równania  x(t)  i  y(t) stanowią podstawę do rozwiązania zadania.

-         równanie toru, tzn. równanie które opisuje tor ciała niezależnie od czasu  t,  otrzymuje się eliminując parametr  t  z równań ruchów składowych.

(odpowiednie przykłady omówione zostały na wykładzie w dn. 16.10.05)

 

 

 

Literatura:

[1] M.A.Herman, A.Kalestyński, L.Widomski, Podstawy fizyki dla kandydatów na wyższe uczelnie i studentów, PWN Warszawa 1999

[2] D.Halliday, R.Resnick, J.Wlker, Podstawy Fizyki tom 1, PWN, Warszawa 2005