2. Rachunek różniczkowy

Definicja pochodnej funkcji

(2.1)

lub inaczej pisząc

(2.2)

Interpretacja geometryczna pochodnej przedstawiona jest na rys. 2.1

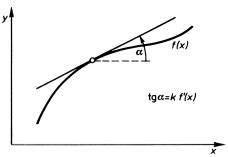
Rys. 2.1. Interpretacja geometryczna pochodnej funkcji

Miarą wartości pochodnej funkcji w punkcie x=x0 jest tangens kąta nachylenia stycznej do krzywej w tym punkcie przy czym kąt nachylenia mierzy się od osi OX w kierunku przeciwnym do ruchu wskazówek zegara.

Pochodna funkcji przemnożonej przez stałą

(2.3)

Pochodna sumy (różnicy) dwóch funkcji

(2.4)

Pochodna iloczynu dwóch funkcji

(2.5)

Pochodna ilorazu dwóch funkcji

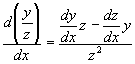(2.6)

Pochodna funkcji złożonej: jeżeli oraz

(2.7)

Pochodne niektórych funkcji elementarnych:

(2.8)

(2.9)

(2.10)

(2.11)

(2.12)

(2.13)

(2.14)

(2.15)

Literatura:

M.A.Herman, A.Kalestyński, L.Widomski, Podstawy fizyki dla kandydatów na wyższe uczelnie i studentów, PWN Warszawa 1999