Wielkości fizyczne, jednostki1.2 Wektory
W fizyce mamy do czynienia zarówno z wielkościami skalarnymi jak i wielkościami wektorowymi. Wielkości skalarne takie jak np. masa, objętość, czas, ładunek, temperatura, praca, mają jedynie wartość. Natomiast wielkości wektorowe np. prędkość, przyspieszenie, siła, pęd, natężenie pola, posiadają wartość, kierunek, zwrot. Poniżej przypominamy podstawowe działania na wektorach.
Rozkładanie wektorów na składowe
W działaniach na wektorach operuje się składowymi tych wektorów wyznaczonymi w wybranym układzie odniesienia. Składowe wektora wyznaczamy umieszczając początek wektora w początku układu współrzędnych i rzutując koniec wektora na poszczególne osie wybranego układu współrzędnych.
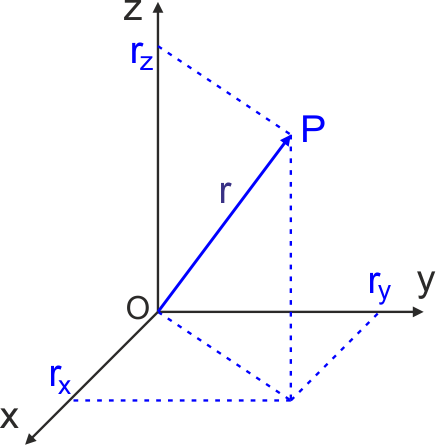
Rys. 1.1. Wektor r i jego składowe rx, ry, rz w pewnym układzie współrzędnych
Suma wektorów
W wybranym układzie współrzędnych wektor jest definiowany przez podanie jego współrzędnych np.
Zwróćmy w tym miejscu uwagę na przyjętą konwencję. Wszystkie wektory wyróżnione są w tekście czcionką wytłuszczoną.
Sumą dwóch wektorów jest nowy wektor o współrzędnych
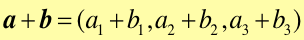
Geometrycznie jest to przekątna równoległoboku zbudowanego na tych wektorach. Różnicę dwóch wektorów przedstawia druga przekątna (rysunek poniżej).
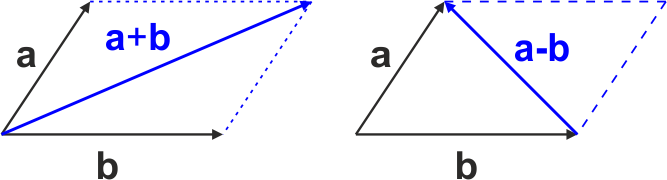
Rys. 1.2. Suma i różnica wektorów
Iloczyn skalarny dwóch wektorów
Iloczyn skalarny dwóch wektorów a · b jest liczbą (skalarem) równą iloczynowi wartości bezwzględnych (długości) tych wektorów pomnożony przez cosinus kąta między nimi.
Iloczyn skalarny jest często stosowany do opisu wielkości fizycznych. Przykładem wielkości fizycznej, którą można przedstawić jako iloczyn skalarny dwóch wielkości wektorowych jest praca. Praca jest iloczynem skalarnym siły i przesunięcia.
Iloczyn wektorowy
Iloczyn wektorowy dwóch wektorów axb jest nowym wektorem c, którego długość (wartość bezwzględna) jest równa iloczynowi długości tych wektorów i sinusa kąta pomiędzy nimi
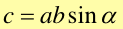
Wektor c jest prostopadły do płaszczyzny wyznaczonej przez wektory a i b. Zwrot jego jest określony regułą śruby prawoskrętnej lub regułą prawej ręki. Jeżeli palce prawej ręki zginają się w kierunku obrotu wektora a do wektora b (po mniejszym łuku) to kciuk wskazuje kierunek wektora c = a x b tak jak na rysunku poniżej
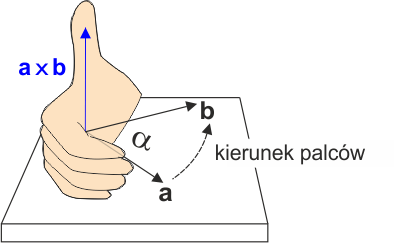
Rys. 1.3. Iloczyn wektorowy