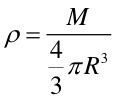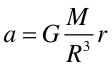Pole grawitacyjne wewnątrz kuli
Rozpatrzmy pole grawitacyjne wytwarzane przez sferę (czaszę)
kulistą o masie m i promieniu R. Dla r > R
(na zewnątrz sfery) pole grawitacyjne ma wartość Gm/r 2
to znaczy jest takie jakby cała masa była skupiona w środku sfery. Jakie
jest jednak pole wewnątrz sfery?
Rozważmy przyczynki od dwóch leżących naprzeciwko siebie elementów
powierzchni S1 i S2 w dowolnym
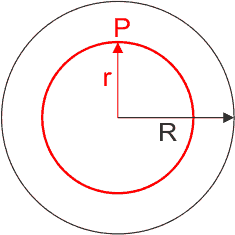
punkcie P wewnątrz sfery tak jak na rysunku poniżej.
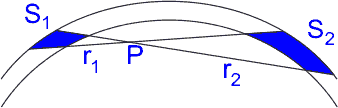
Rys. 1. Punkt P wewnątrz cienkiej sfery
Fragment S1 czaszy jest źródłem siły F1 ~ S1/(r1)2 działającej w lewo. Powierzchnia S2 jest źródłem siły działającej w prawo F2 ~ S2/(r2)2. Otrzymujemy więc
|
(1) |
Z rozważań geometrycznych wynika natomiast, że
|
(2) |
Po podstawieniu do pierwszego równania otrzymujemy
|
(3) |
Tak więc wkłady wnoszone przez elementy powierzchni S1 i S2 znoszą się. Można w ten sposób podzielić całą sferę i pokazać, że siła wypadkowa jest równa zeru. Tak więc wewnątrz sfery pole grawitacyjne jest równe zeru. Pole wewnątrz czaszy mającej skorupę dowolnej grubości też jest zero bo zawsze możemy podzielić tę skorupę na szereg cienkich warstw koncentrycznych.
| Na rysunku obok przedstawiono pełną kulę o promieniu R i masie M. W punkcie P pole grawitacyjne pochodzące od zewnętrznej warstwy jest równe zeru. Pole grawitacyjne pochodzi więc tylko od kuli o promieniu r czyli |
|
|
|
(4) | |
| gdzie m jest masą kuli o promieniu r. Dla jednorodnej kuli o gęstości r równanie przyjmuje postać | ||
|
(5) |
Uwzględniając, że
|
(6) |
Otrzymujemy ostatecznie
|
(7) |
Widzimy, że wewnątrz kuli przyspieszenie grawitacyjne (natężenie pola grawitacyjnego) i co za tym idzie siła zmieniają się liniowo z odległością r od środka (wykres poniżej)
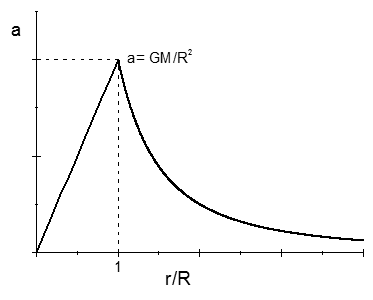
Rys. 2. Pole grawitacyjne jednorodnej kuli w funkcji odległości od środka


 Pole grawitacyjne, pola sił
Pole grawitacyjne, pola sił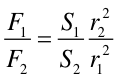
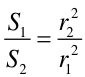
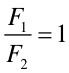
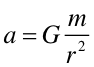
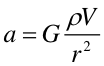
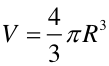 i
i