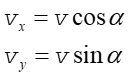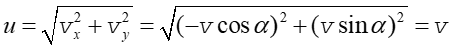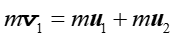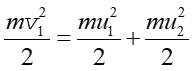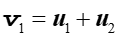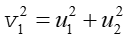10. Zderzenia
• Spis treści  
• Podsumowanie  
•   Zderzenia w przestrzeni 1-wymiarowej

10.2 Zderzenia na płaszczyźnie

   Dotychczas zajmowaliśmy się zderzeniami cząstek w przestrzeni jednowymiarowej. Teraz rozpatrzymy najprostszy przypadek wielowymiarowy; zajmiemy się zderzeniami sprężystymi na płaszczyźnie. Zaczniemy od analizy zderzenia sprężystego ukośnego kuli o masie m i prędkości v ze ścianą. Naszym celem jest znalezienie prędkości kuli po zderzeniu. 
Ruch kuli opisujemy w układzie współrzędnych x i y związanym ze ścianą, oś x pokazuje kierunek prostopadły do ściany,  y - kierunek równoległy, a początek układu umieszczamy na powierzchni ściany w punkcie zderzenia. W tak wybranym układzie współrzędnych rozkładamy na składowe wektor prędkości v (rysunek poniżej)

Na przykładzie rzutu ukośnego (rozdział 3.2) pokazaliśmy, że taki ruch na płaszczyźnie można traktować jak dwa niezależne ruchy jednowymiarowe. Ruch kuli w kierunku y odbywa się równolegle do ściany więc składowa v_y nie ulega zmianie przy odbiciu. Natomiast składowa prostopadła do powierzchni ściany, po zderzeniu zmienia znak na przeciwny, kula odbija się od ściany (jak w przykładzie b) w poprzednim rozdziale. Stąd prędkość kuli po zderzeniu (odbiciu się od ściany)

Prędkość po odbiciu od ściany jest taka sama jak przed odbiciem, a kąt odbicia jest równy kątowi padania. Ruch kuli możesz prześledzić na rysunku-animacji poniżej. Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

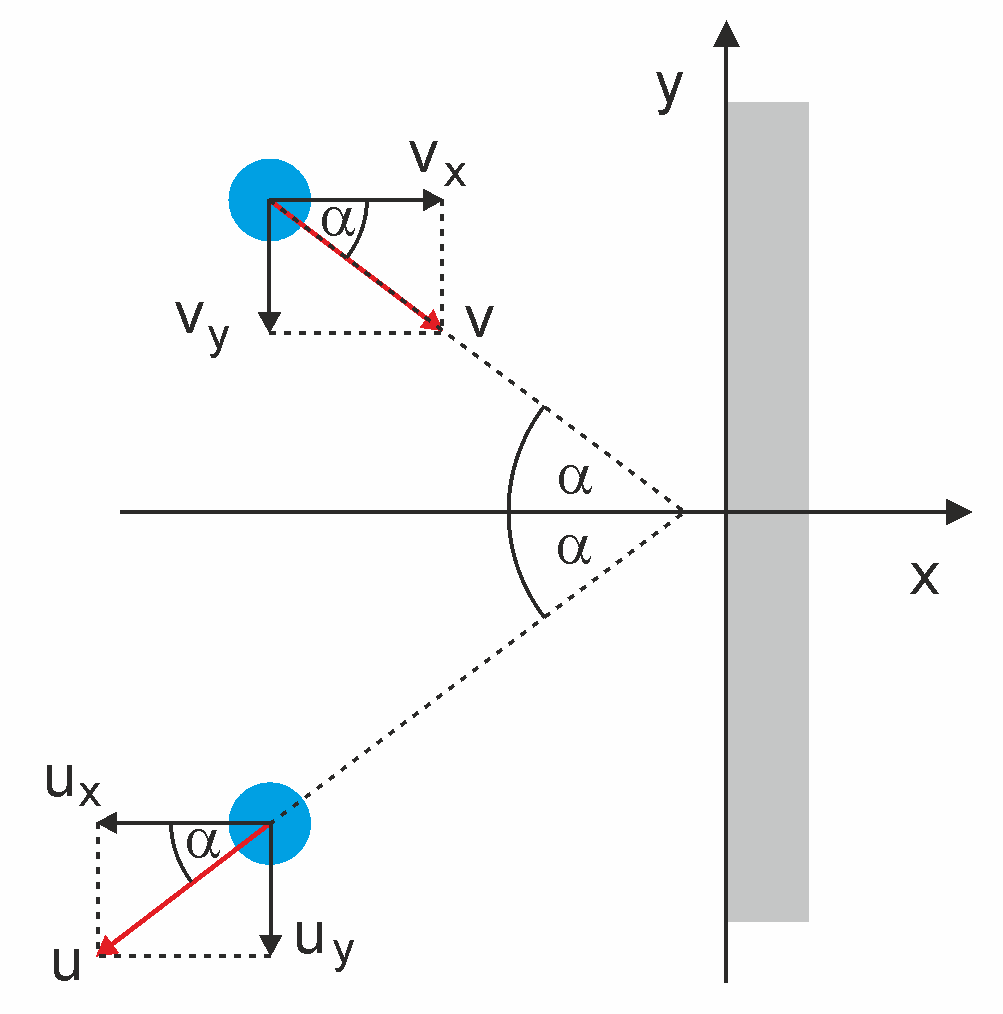
 Rys. 10.4. Sprężyste zderzenie kuli ze ścianą

Teraz rozpatrzymy ukośne, sprężyste zderzenie kuli bilardowej poruszającej się z prędkością v₁ z drugą identyczną spoczywająca kulą. Takie zagranie stosuje się, żeby skierować wybraną kulę pod pewnym kątem w bok. Dzieje się tak, gdy środek kuli spoczywającej nie leży na linii wzdłuż, której porusza się pierwsza kula. Takie zderzenie możesz prześledzić na animacji poniżej. Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

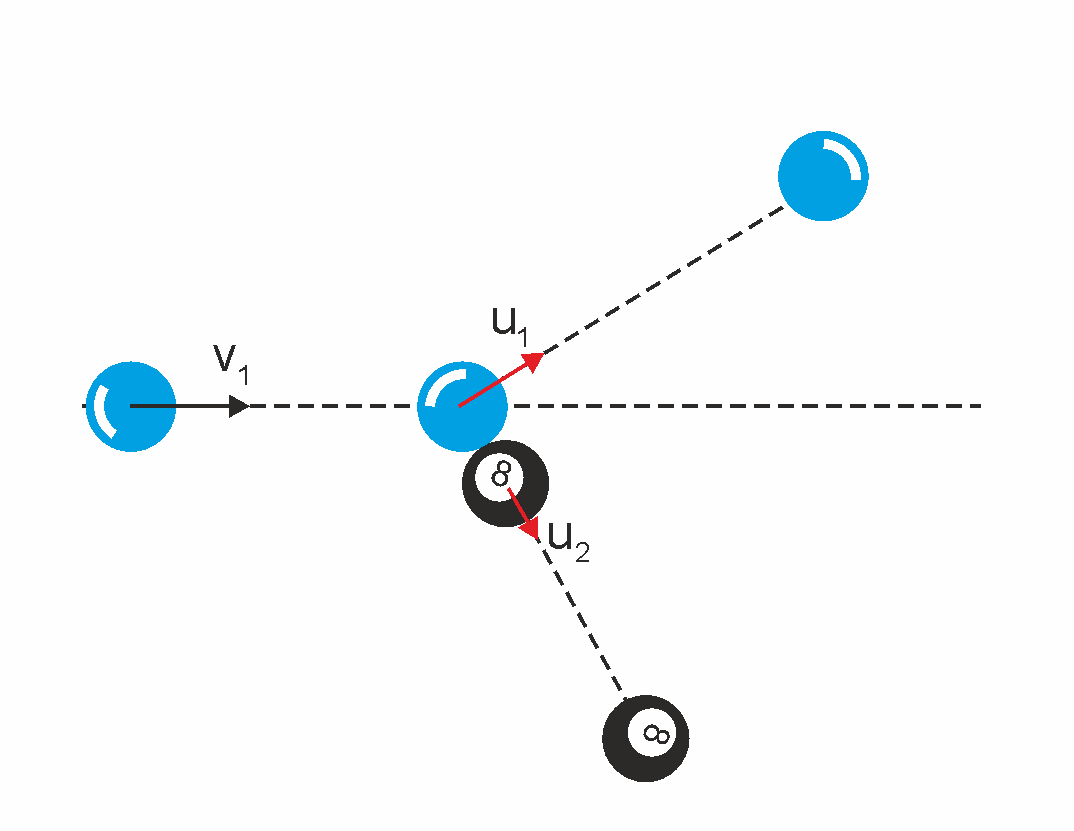
 Rys. 10.5. Zderzenie kul bilardowych

Zgodnie z zasadą zachowania pędu i zasadą zachowania energii

Z równań tych wynika, że wektory v₁, u₁ i u₂ tworzą boki trójkąta prostokątnego (twierdzenie Pitagorasa) tak jak na rysunku 10.6.

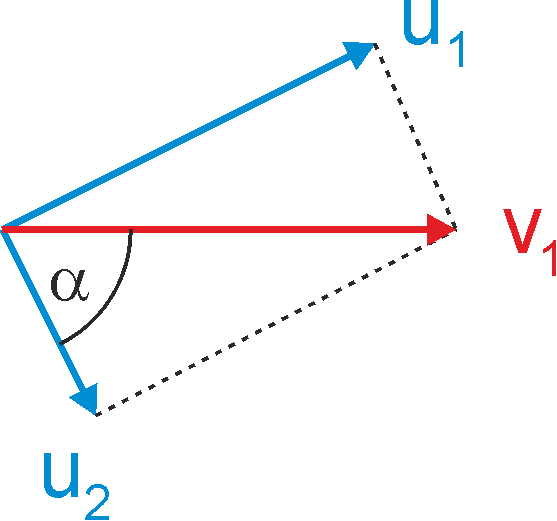
 Rys. 10.6. Prędkości kul przed i po zderzeniu

Oznacza to, że dla dowolnego kąta α  < (0,π/2) po zderzeniu kule będą zawsze poruszały się względem siebie  pod kątem prostym. Wartość kąta α zależy natomiast od tak zwanego parametru zderzenia czyli odległości między pierwotnym kierunkiem ruchu kuli pierwszej, a środkiem kuli spoczywającej.

Ten rozdział kończy drugi moduł; możesz teraz przejść do podsumowania i zadań testowych.