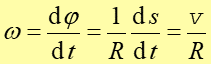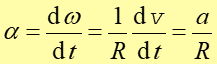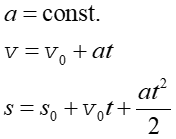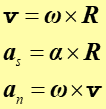Test W naszych dotychczasowych rozważaniach nad ruchem ciał
traktowaliśmy je jako punkty materialne tzn. jako obiekty obdarzone masą,
których rozmiary możemy zaniedbać. Jednak rzeczywiste ciała w ruchu mogą
się obracać czy wykonywać drgania. W kolejnych rozdziałach zajmiemy się
właśnie ruchem obrotowym i drgającym ciał.
Będziemy rozważać ruch obrotowy ciał sztywnych tj. obiektów, w których
odległości wzajemne punktów są stałe. Zajmiemy się również bardziej
ogólnym przypadkiem, w którym ciało sztywne wykonuje zarówno ruch postępowy
jak i obrotowy.
11.1 Kinematyka ruchu obrotowego
Nasze rozważania zaczniemy od wyprowadzenia równań
kinematyki ruchu obrotowego, podobnych do równań kinematyki ruchu postępowego.
W ruchu obrotowym wielkością analogiczną do przesunięcia jest przesunięcie
kątowe φ
.
Kąt φ określa położenie (kątowe) punktu P
względem układu odniesienia (rysunek 11.1).
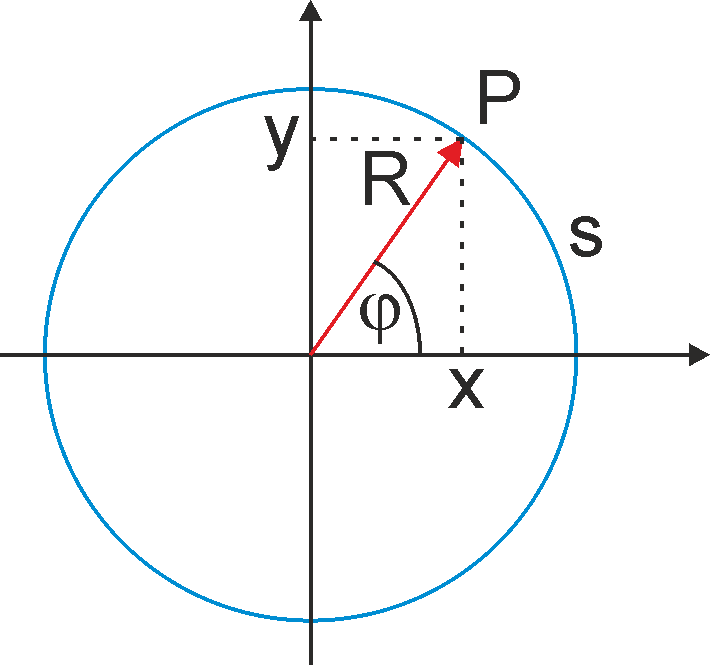
Rys. 11.1. Punkt P obracającego się ciała zatacza łuk o długości s
Związek φ = s/R między drogą liniową s,
a przesunięciem kątowym φ
wynika bezpośrednio z miary łukowej kąta φ.
W ruchu obrotowym wielkością analogiczną chwilowej prędkości liniowej v
jest chwilowa prędkość kątowa ω
|
(11.1) |
W ruchu obrotowym podobnie jak w ruchu po okręgu ω
jest też nazywana częstością kątową
i jest związana z częstotliwością f relacją
|
(11.2) |
Podobnie jak chwilowe przyspieszenie liniowe a zostało zdefiniowane chwilowe
przyspieszenie kątowe α
|
(11.3) |
Możemy teraz podać opis ruchu obrotowego ze stałym przyspieszeniem kątowym α poprzez analogię do ruchu postępowego jednostajnie zmiennego.
Tab. 11.1.Porównanie ruchu postępowego i obrotowego
| Ruch postępowy | Ruch obrotowy |
|---|---|
|
|
Pamiętajmy, że zarówno prędkość kątowa jak i przyspieszenie kątowe są wektorami. Na rysunku 11.2 poniżej, pokazane są wektory: prędkości liniowej v, prędkości kątowej ω, przyspieszenia stycznego as, przyspieszenia normalnego an i przyspieszenia kątowego α punktu P obracającego się ciała sztywnego. Punkt P porusza się ruchem przyspieszonym po okręgu.
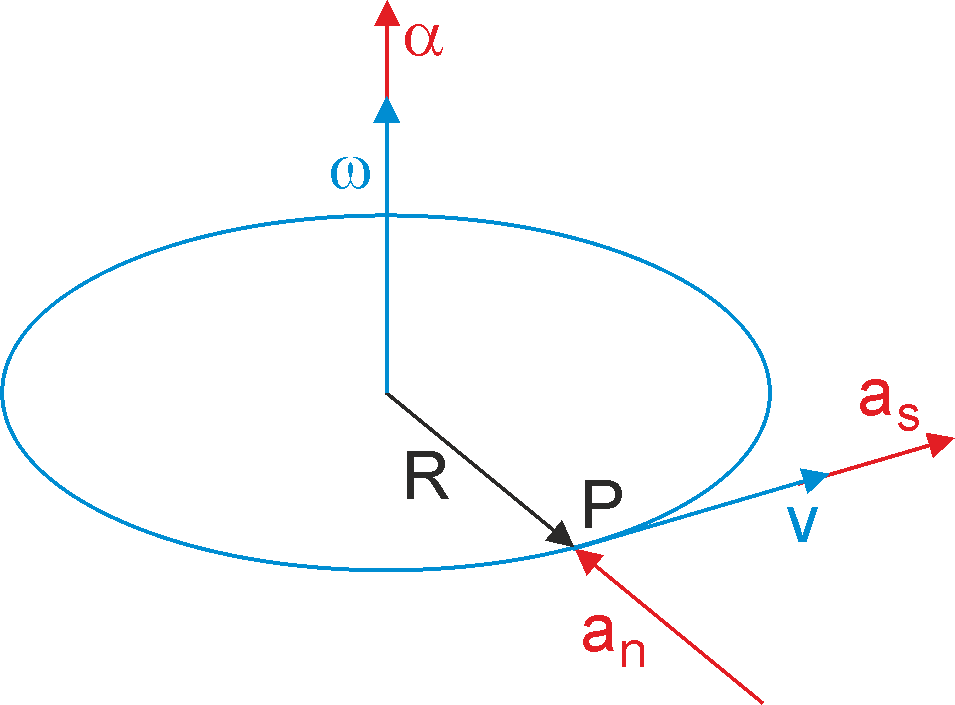
Rys. 11.2. Kierunki wektorów v, ω, as, an i α
Związki pomiędzy wielkościami liniowymi i kątowymi w postaci skalarnej są dane równaniami (11.1), (11.3) oraz równaniem (3.14). Natomiast te zależności w postaci wektorowej mają postać
|
(11.4) |
Więcej o ... ruchu przyspieszonym po okręgu.
|
Jednostki Z powyższych rozważań wynika, że jeżeli kąt φ jest mierzony w radianach (rad) to jednostką prędkości kątowej ω jest radian na sekundę (rad/s), a przyspieszenia kątowego α radian na sekundę do kwadratu (rad/s2). |
Na zakończenie spróbuj wykonać następujące ćwiczenie.
|
Ćwiczenie W wielu czytnikach CD płyta ma stałą prędkość liniową natomiast zmienia się jej prędkość kątowa. Dzięki tej stałej prędkości liniowej można zachować jednakowo gęste upakowanie informacji na całym dysku. Ta prędkość dla dysku audio (pojedynczej prędkości) wynosi 1.25 m/s. Całkowita długość spiralnie naniesionej ścieżki wynosi 5.55 km. Średnica zewnętrzna dysku jest równa 12 cm, a wewnętrzna 2.5 cm. Oblicz maksymalną i minimalną prędkość kątową dysku. Jakie jest średnie przyspieszenie kątowe płyty podczas jej ciągłego, całkowitego odczytu? Pamiętaj o odpowiednich jednostkach. Sprawdź obliczenia i wynik. |
