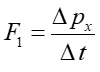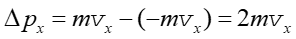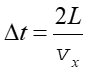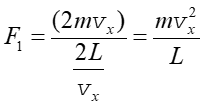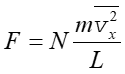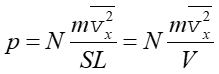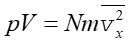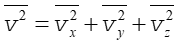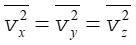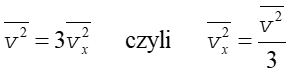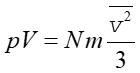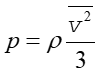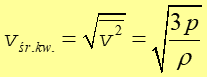15. Kinetyczna teoria gazów i termodynamika I
• Spis treści  
• Temperatura, równanie stanu gazu doskonałego  
•   Test

  Termodynamika zajmuje się właściwościami cieplnymi układów makroskopowych, zaniedbując w odróżnieniu od mechaniki statystycznej mikroskopową budowę ciał tworzących układ. Gdybyśmy chcieli ściśle określić stan fizyczny układu zawierającego ogromną liczbę cząsteczek, na przykład porcji gazu, to musielibyśmy znać stan każdej cząsteczki oddzielnie to znaczy musielibyśmy podać położenie każdej cząsteczki, jej prędkość oraz siły nań działające. Takie obliczenia ze względu na dużą liczbę cząsteczek są niemożliwe. Okazuje się jednak, że posługując się metodami statystycznymi (rachunkiem prawdopodobieństwa) możemy znaleźć związki między wielkościami mikroskopowymi (dotyczącymi poszczególnych cząsteczek), a wielkościami makroskopowymi opisującymi cały układ. Chcąc opisać gaz jako całość możemy więc badać jedynie wielkości makroskopowe takie jak ciśnienie, temperatura czy objętość bez wdawania się w zachowanie poszczególnych cząsteczek.

15.1 Ciśnienie gazu doskonałego

Rozpocznijmy nasze rozważania od definicji gazu doskonałego. Zrobimy to podając następujące założenia dotyczące cząsteczek gazów:

Wyprowadzimy teraz prawo gazów doskonałych. Cząsteczki gazu będziemy traktować jako N małych, twardych kulek, każda o masie m zamkniętych w sześciennym pudełku o objętości V. Kulki są twarde to znaczy będą zderzały się sprężyście ze ściankami naczynia, a to oznacza, że ich energia kinetyczna będzie stała. Na początek rozważmy jedną cząsteczkę, która zderza się ze ścianką naczynia (rysunek 15.1).

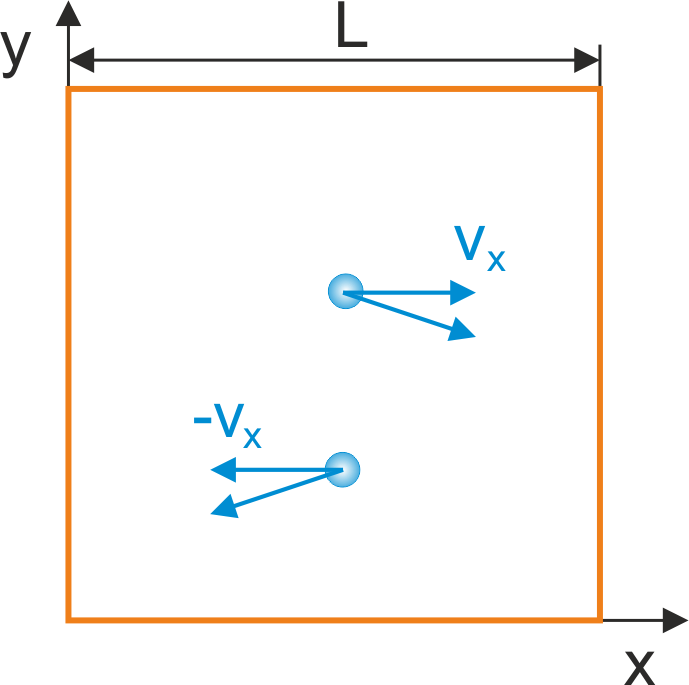
 Rys. 15.1. Cząsteczka gazu odbija się sprężyście od ścianki naczynia

Siła jaką cząsteczka wywiera na ściankę w czasie Δt wynosi zgodnie z drugą zasadą dynamiki Newtona

Zmiana składowej x pędu cząsteczki spowodowana zderzeniem wynosi

Cząsteczka po odbiciu dociera do ścianki przeciwnej i powraca. Jeżeli po drodze nie zderza się z innymi cząsteczkami to czas pomiędzy kolejnymi zderzeniami z wybraną ścianką jest równy czasowi przelotu przez cały sześcian i z powrotem

gdzie L jest odległością między ściankami. Stąd siła wywierana na ściankę (przez jedną cząsteczkę) wynosi

Dla N cząstek całkowita siła wynosi

gdzie jest to uśrednione po wszystkich cząsteczkach. Dzieląc obie strony równania przez pole powierzchni ścianki S = L²  otrzymujemy ciśnienie

Jak widać iloczyn pV jest stały tak długo jak długo jest stała energia kinetyczna cząstek.

Prędkość średnią kwadratową cząsteczki możemy zapisać jako

Zauważmy ponadto, że cząsteczki gazu wykonują ruch chaotyczny więc poruszają się we wszystkich kierunkach, a żaden nie jest wyróżniony. Dlatego zachodzi równość

Podstawiamy to wyrażenie do równania (15.7) i otrzymujemy

Ponieważ iloczyn Nm jest równy masie gazu M, to korzystając z wyrażenia na gęstość ρ = M/V można przepisać powyższe równanie w postaci