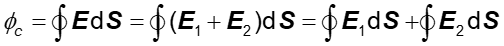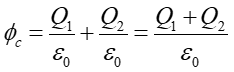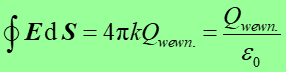Strumień pola elektrycznego18.2 Prawo Gaussa
Rozpatrzmy zamkniętą powierzchnię obejmującą dwa ładunki Q1 i Q2. Całkowity strumień (liczba linii sił) przechodzący przez powierzchnię otaczającą ładunki Q1 i Q2 jest równy
|
(18.6) |
gdzie pole E1 jest wytwarzane przez Q1, a pole E2 przez Q2. Kółko na znaku całki oznacza, że powierzchnia całkowania jest zamknięta. Korzystając z otrzymanego wcześniej wyniku (18.5) mamy
|
(18.7) |
Całkowity strumień pola elektrycznego przez zamkniętą powierzchnię jest więc równy całkowitemu ładunkowi otoczonemu przez tę powierzchnię podzielonemu przez ε0. Analogiczne rozumowanie można przeprowadzić dla dowolnej liczby ładunków wewnątrz dowolnej zamkniętej powierzchni. Otrzymujemy więc ogólny związek znany jako prawo Gaussa
|
Prawo, zasada, twierdzenie |
|
(18.8) |
Strumień wychodzący z naładowanego ciała jest równy wypadkowemu ładunkowi tego ciała podzielonemu przez ε0. Jeżeli wypadkowy ładunek ciała jest ujemny to strumień pola elektrycznego, tak jak i linie pola, wpływa do ciała. Natomiast gdy ładunek wypadkowy wewnątrz zamkniętej powierzchni jest równy zeru to całkowity strumień też jest równy zeru; tyle samo linii pola wpływa jak i wypływa przez powierzchnię Gaussa. Podobnie jest w sytuacji gdy ładunki znajdują się na zewnątrz zamkniętej powierzchni. Te sytuacje są pokazane na rysunku 18.4 poniżej.
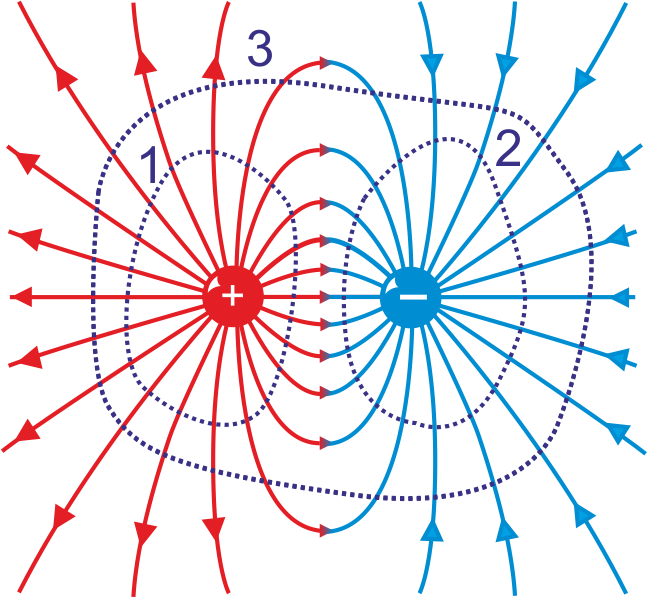
Rys. 18.4. Powierzchnie Gaussa wokół ładunków dodatnich i ujemnych
Całkowit strumień przez powierzchnię "1" jest dodatni, strumień przez powierzchnię "2" jest ujemny, a strumień przez powierzchnię "3" jest równy zeru.
Teraz przejdziemy do zastosowania prawa Gaussa do obliczania natężenia pola E dla różnych naładowanych ciał.