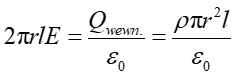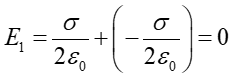Przykłady zastosowania prawa Gaussa II

18.4 Przykłady zastosowania prawa Gaussa II

Liniowy rozkład ładunków

Obliczymy teraz pole E w odległości r od jednorodnie naładowanego pręta (drutu) o długościl >> r. W tym celu wprowadzamy liniową gęstość ładunku λ równą ilości ładunku przypadającego na jednostkę długości pręta λ = Q / l. Ze względu na symetrię układu jako powierzchnię Gaussa wybierzmy walec (oczywiście można wybrać dowolny kształt) o promieniu r większym od promienia pręta R bo chcemy policzyć pole na zewnątrz pręta (rysunek 18.9).

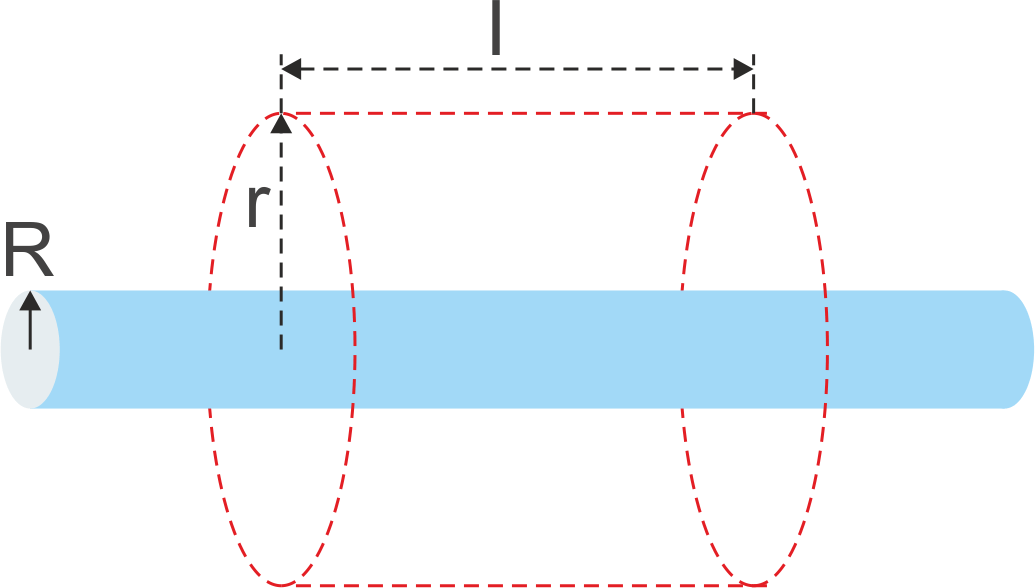
Rys. 18.9. Pręt naładowany z gęstością liniową λ

Z prawa Gaussa

(18.18)

Ze względu na symetrię pole elektryczne E jest skierowane radialnie względem pręta, tzn. jest prostopadłe do bocznej powierzchni walca (powierzchni Gaussa). Strumień pola E przez podstawy walca jest więc równy zeru bo E leży na powierzchni. Ponadto pole elektryczne ma taką samą wartość w każdym punkcie powierzchni bocznej walca więc spełnione jest równanie

(18.19)

lub

(18.20)

Teraz obliczymy pole wewnątrz jednorodnie naładowanego pręta. Ponownie wybieramy powierzchnię Gaussa w kształcie walca ale o promieniu r < R. Wprowadzamy gęstość objętościową ładunku ρ równą ładunkowi przypadającemu na jednostkę objętości. Możemy teraz zapisać ładunek zamknięty wewnątrz powierzchni Gaussa

(18.21)

Z prawa Gaussa otrzymujemy

(18.22)

a stąd

(18.23)

Pole rośnie liniowo w miarę oddalania się od środka pręta.

Płaskie rozkłady ładunków

Teraz obliczymy pole od nieskończonej, jednorodnie naładowanej płaszczyzny. W tym celu wprowadzamy powierzchniową gęstość ładunku σ równą ilości ładunku przypadającego na jednostkę powierzchni. Powierzchnię Gaussa wybieramy na przykład w postaci walca takiego jak na rysunku 18.10.

Rys. 18.10. Jednorodnie naładowana nieskończona płaszczyzna

Ładunek otoczony przez powierzchnię Gaussa jest równy Q_wewn. = σS, gdzie σ jest gęstością powierzchniową, a S powierzchnią podstawy walca. Z symetrii wynika, że pole E jest prostopadłe do płaszczyzny więc nie przecina bocznej powierzchni walca (strumień przez boczną powierzchnię jest równy zeru). Z prawa Gaussa otrzymujemy

(18.24)

gdzie czynnik 2 odpowiada dwóm podstawom walca (linie pola wychodzą w obie strony). Ostatecznie więc

(18.25)

W praktyce stosuje się, pokazany na rysunku 18.11, układ dwóch płaskich równoległych płyt naładowanych ładunkami jednakowej wielkości ale o przeciwnych znakach (kondensator płaski ).

Rys. 18.11. Pole między równoległymi płytami naładowanymi ładunkami tej samej wielkości ale o przeciwnych znakach

Pole wytwarzane przez płytę naładowaną ładunkiem dodatnim jest równe E₊ = σ/2ε₀ i skierowane od płyty. Natomiast pole wytwarzane przez płytę naładowaną ujemnie ma tę samą wartość E₋ = σ/2 ε₀ ale skierowane jest do płyty. Zatem w obszarze (I)

(18.26)

w obszarze (II)

(18.27)

w obszarze (III)

(18.28)

Widzimy, że na zewnątrz układu pole jest równe zeru a pomiędzy płytami ma w każdym punkcie stałą wartość σ/ε₀. Takie pole nazywamy polem jednorodnym.

Powierzchnia przewodnika

Sytuacja jest inna jeżeli naładowana powierzchnia stanowi część powierzchni przewodnika na przykład tak jak na rysunku 18.12.

Rys. 18.12. Element powierzchni przewodnika

Ponieważ cały ładunek gromadzi się na zewnętrznej powierzchni to wewnątrz pole E = 0. Co więcej E musi być prostopadłe do powierzchni bo gdyby istniała składowa styczna do powierzchni to elektrony poruszałyby się po niej. Ponownie, jak w przypadku nieskończonej naładowanej płaszczyzny wybieramy powierzchnię Gaussa w kształcie walca (rysunek 18.11) ale tym razem linie pole wychodzą tylko przez jedną podstawę walca S, na zewnątrz. Z prawa Gaussa wynika, że

(18.29)

a stąd

(18.30)

na powierzchni przewodnika.