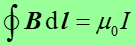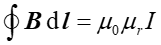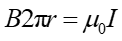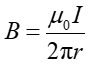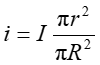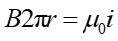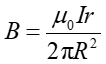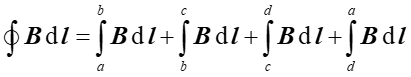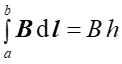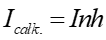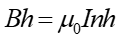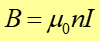23. Pole magnetyczne przewodników z prądem
• Spis treści  
• Oddziaływanie równoległych przewodników z prądem  
•   Efekt Halla

23.1 Prawo Ampère'a

Pole wokół przewodnika z prądem

  Jak już mówiliśmy, doświadczalnie można wyznaczyć linie pola magnetycznego przy użyciu np. opiłków żelaza, które zachowują się jak dipole magnetyczne. Opiłki ustawiają się zgodnie z kierunkiem B i dają obraz linii pola magnetycznego. Na rysunku 23.1 pokazany jest rozkład opiłków żelaza wokół prostoliniowego przewodnika z prądem.

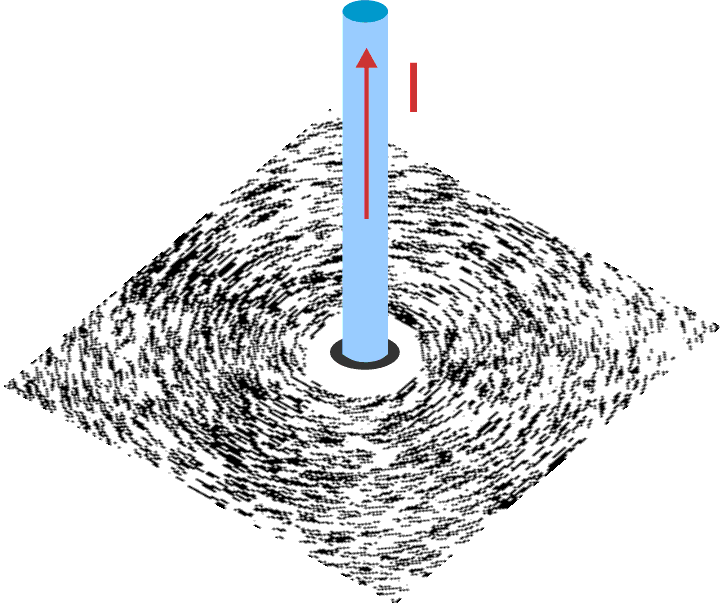
 Rys. 23.1. Opiłki żelaza rozsypane na powierzchni kartki umieszczonej prostopadle do przewodnika z prądem
tworzą koncentryczne kręgi odzwierciedlając kształt linii pola magnetycznego

Widzimy więc, że linie pola B wytwarzanego przez przewodnik są zamkniętymi współśrodkowymi okręgami w płaszczyźnie prostopadłej do przewodnika tak jak pokazanona rysunku poniżej. Wektor B jest styczny do tych linii pola w każdym punkcie.

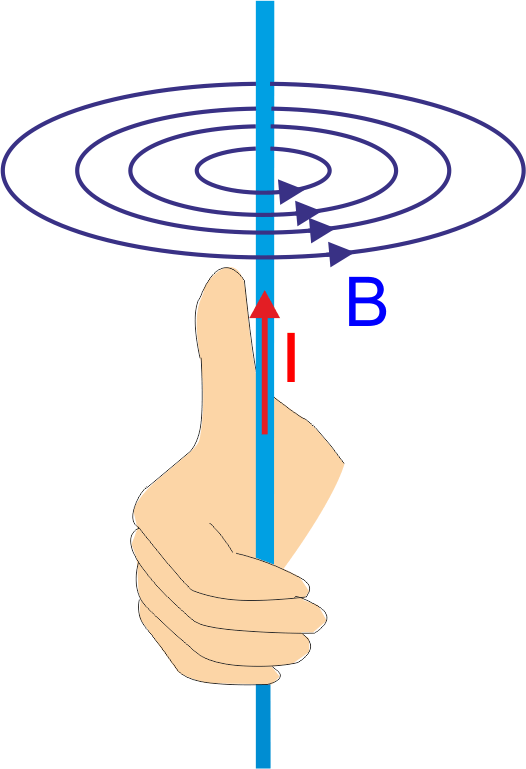
 Rys. 23.2. Linie pola magnetycznego wokół prostoliniowego przewodnika z prądem

Zwrot wektora indukcji B wokół przewodnika wyznaczamy stosując następującą zasadę: jeśli kciuk prawej ręki wskazuje kierunek prądu I, to zgięte palce wskazują kierunek B (linie pola B krążą wokół prądu). Natomiast wartość pola B wokół przewodnika z prądem można obliczyć z korzystając z prawa Ampère'a.

Prawo Ampère'a

Chcemy teraz znaleźć pole magnetyczne wytwarzane przez powszechnie występujące rozkłady prądów, takie jak przewodniki prostoliniowe, cewki itp. Potrzebujemy prawa analogicznego do prawa Gaussa, które pozwalało na podstawie znajomości ładunku (źródła pola E) wyznaczyć natężenie pola E. Dla pola magnetycznego szukamy związku pomiędzy prądem (źródłem pola B) a indukcją magnetyczną. Taki związek jest wyrażony poprzez prawo Ampère'a.

Pokazaliśmy, że linie pole magnetycznego wokół przewodnika z prądem stanowią zamknięte okręgi. Stąd, zamiast sumowania (całki) po zamkniętej powierzchni (jak w prawie Gaussa), w prawie Ampère'a sumujemy (całkujemy) po zamkniętym konturze (liczymy całkę krzywoliniową). Taka całka powierzchniowa dla pola E równała się wypadkowemu ładunkowi wewnątrz powierzchni, a w przypadku pola B jest równa całkowitemu prądowi I otoczonemu przez kontur.
Tak jak w przypadku prawa Gaussa wynik był prawdziwy dla dowolnej powierzchni zamkniętej, tak dla prawa Ampère'a wynik nie zależy od kształtu konturu zamkniętego.

Stała μ₀ = 4π·10⁻⁷ Tm/A, jest tzw. przenikalnością magnetyczną próżni . Gdy pole magnetyczne jest wytworzone nie w próżni ale w jakimś ośrodku to fakt ten uwzględniamy wprowadzając stałą materiałową  μ_r, zwaną względną przenikalnością magnetyczną ośrodka tak, że prawo Ampère'a przyjmuje postać

Przykład - prostoliniowy przewodnik

Jako przykład obliczymy pole w odległości r od nieskończenie długiego prostoliniowego przewodnika, w którym płynie prąd o natężeniu I (rysunek 23.3). Ponieważ linie pola B  wytwarzanego przez przewodnik są współśrodkowymi okręgami więc jako drogę całkowania wybieramy okrąg o promieniu r. W każdym punkcie naszego konturu pole B jest do niego styczne (równoległe do elementu konturu dl ).

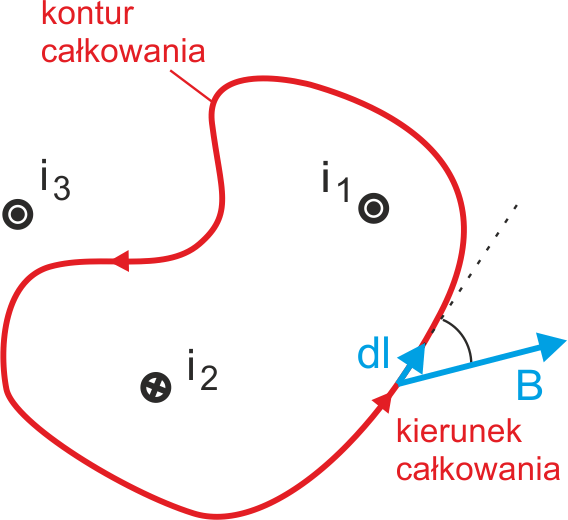
 Rys. 23.3. Kontur kołowy o promieniu r wokół przewodnika z prądem

Wówczas na podstawie prawa Ampère'a

W ten sposób obliczyliśmy pole B na zewnątrz przewodnika. Wartość pola jest taka jakby cały prąd płynął przez środek przewodnika.

Natomiast jeżeli chcemy obliczyć pole wewnątrz przewodnika (pręta) to wybieramy kontur kołowy o promieniu r < R, gdzie R jest promieniem przewodnika. Wewnątrz konturu przepływa prąd i będący częścią całkowitego prądu I

Na podstawie prawa Ampère'a dla takiego konturu

skąd, po uwzględnieniu zależności (23.5)  otrzymujemy

Pole magnetyczne wewnątrz nieskończonego, prostoliniowego przewodnika z prądem rośnie proporcjonalnie do r w miarę przechodzenia od środka do powierzchni przewodnika.

Przykład - cewka (solenoid)

Zastosujemy teraz prawo Ampère'a do obliczenia pola magnetycznego wewnątrz cewki przez którą płynie prąd o natężeniu I (rysunek 23.4).

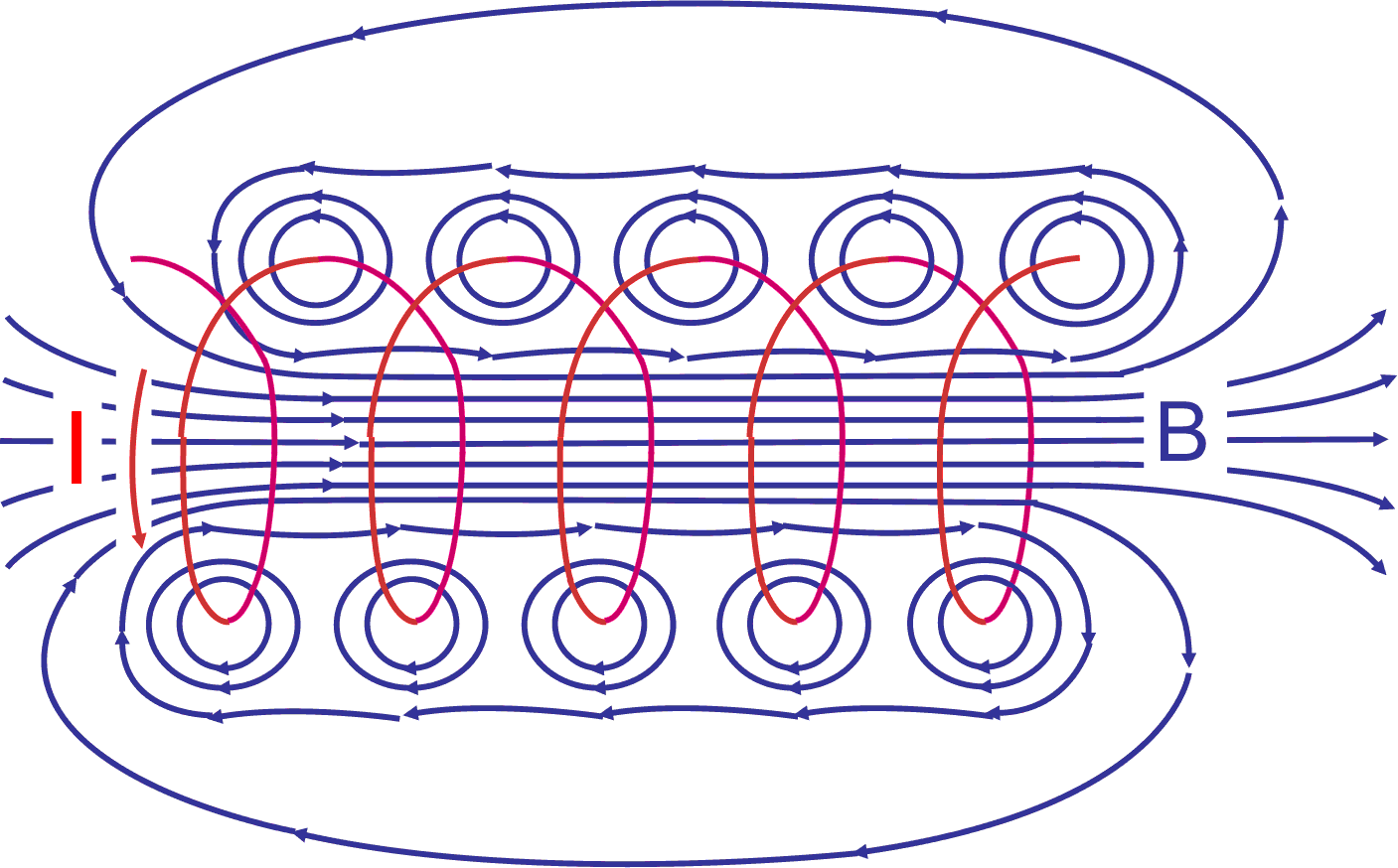
 Rys. 23.4. Pole magnetyczne B wytworzone przez prąd I przepływający przez cewkę

Pole magnetyczne wytworzone przez całą cewkę jest sumą wektorową pól wytwarzanych przez wszystkie zwoje. W punktach na zewnątrz cewki pole wytworzone przez części górne i dolne zwojów znosi się częściowo, natomiast wewnątrz cewki pola wytworzone przez poszczególne zwoje sumują się.

Jeżeli mamy do czynienia z solenoidem tj. z cewką o ciasno przylegających zwojach, której długość jest znacznie większa od jej średnicy to możemy przyjąć, że pole magnetyczne wewnątrz solenoidu jest jednorodne, a na zewnątrz równe zeru. Na rysunku 23.5 pokazany jest przekrój odcinka idealnego solenoidu. Prawo Ampère'a zastosujemy dla konturu zaznaczonego na rysunku linią przerywaną.

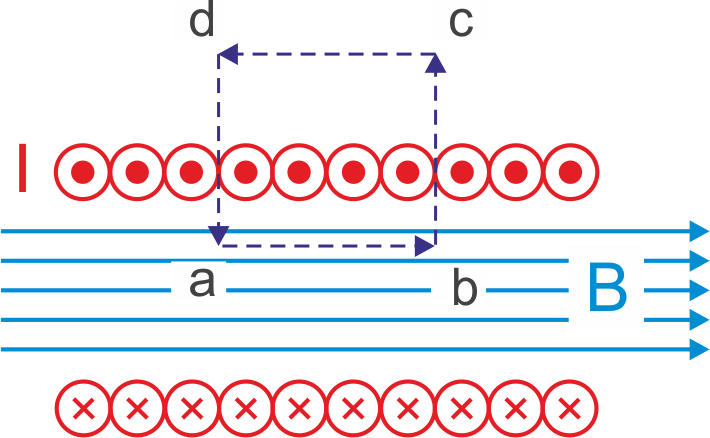
 Rys. 23.5. Zastosowanie prawa Ampère'a do obliczenia pola magnetycznego wewnątrz solenoidu

Całkę krzywoliniową 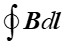przedstawimy jako sumę czterech całek

Całka druga i czwarta są równe zeru bo wektor B jest prostopadły do elementu konturu dl (iloczyn skalarny wektorów prostopadłych jest równy zeru). Trzecia całka też jest równa zeru ale dlatego, że B = 0 na zewnątrz solenoidu. Tak więc niezerowa jest tylko całka pierwsza

gdzie h jest długością odcinka ab. Teraz obliczmy prąd obejmowany przez wybrany kontur. Jeżeli cewka ma n zwojów na jednostkę długości to wewnątrz konturu jest nh zwojów. Oznacza to, że całkowity prąd przez kontur wynosi

gdzie I jest prądem przepływającym przez pojedynczy zwój cewki.

Na podstawie prawa Ampère'a

skąd pole magnetyczne wewnątrz solenoidu

Powyższe równanie stosuje się z powodzeniem również do rzeczywistych cewek (dla punktów z wnętrza cewki, odległych od jej końców)

Cewki stanowią praktyczne źródło jednorodnego pola magnetycznego.