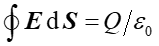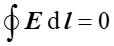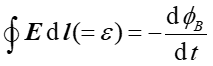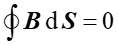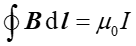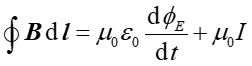Równania Maxwella

W przypadku statycznym (pola niezależne od czasu) dwa równania Maxwella

(1)

oraz

(2)

opisują prawa elektrostatyki. Z pierwszego równania wynika prawo Coulomba, które jest słuszne tylko w przypadku statycznym bo nie opisuje oddziaływania pomiędzy ładunkami w ruchu.

Równanie (2) pokazuje, że gdy nie występuje zmienny (w czasie) strumień magnetyczny, to praca pola E wzdłuż dowolnej zamkniętej drogi jest równa zeru - pole elektrostatyczne jest polem zachowawczym i do jego opisu możemy posłużyć się pojęciem potencjału.

Natomiast w przypadku pól zależnych od czasu równanie to ma postać

(3)

i pole E nie jest polem zachowawczym - nie możemy go opisać za pomocą potencjału.

Kolejne dwa równania Maxwella, w przypadku statycznym (pola niezależne od czasu) opisują prawa magnetostatyki

(4)

oraz

(5)

Pierwsze z tych równań (4) mówi, że nie istnieją ładunki magnetyczne (pojedyncze bieguny) analogiczne do ładunków elektrycznych. Natomiast równanie (5) pokazuje, że źródłem pola magnetostatycznego są stałe prądy elektryczne.

Natomiast w przypadku pól zależnych od czasu równanie to ma postać

(6)

i uwzględnia efekt zmieniających się pól elektrycznych.

Zauważmy, że w przypadku statycznym prawa opisujące pola elektryczne i magnetyczne są od siebie niezależne natomiast w przypadku pól zależnych od czasu równania Maxwella łączą ze sobą pola elektryczne i magnetyczne.