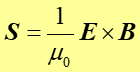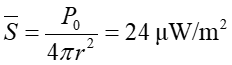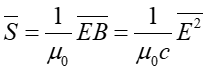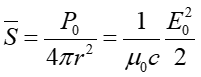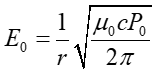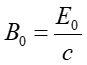Rozchodzenie się fal elektromagnetycznych27.4 Wektor Poyntinga
Fale elektromagnetyczne posiadają zdolność do przenoszenia energii od
punktu do punktu. Szybkość przepływu energii przez jednostkową
powierzchnię płaskiej fali elektromagnetycznej opisujemy wektorem S
zwanym wektorem Poyntinga 
.
Wektor S definiujemy za pomocą iloczynu wektorowego
|
(27.10) |
W układzie SI jest on wyrażony w W/m2, kierunek S pokazuje kierunek przenoszenia energii. Wektory E i B są chwilowymi wartościami pola elektromagnetycznego w rozpatrywanym punkcie.
Przykład
Rozpatrzmy radiostację o mocy P0 = 30 kW wysyłającą fale izotropowo (jednakowo w każdym kierunku). Obliczmy jakie natężenie sygnału (moc na jednostkę powierzchni) odbieramy w odległości r = 10 km od nadajnika i jaka jest amplituda pola elektrycznego i pola magnetycznego docierającej fali elektromagnetycznej.
Ponieważ moc emitowana jest we wszystkich kierunkach tzn. jest równomiernie rozłożona na powierzchni sfery więc średnia wartość wektora Poyntinga w odległości r od źródła ma wartość
|
(27.11) |
Na podstawie wyrażenia (27.4) E = cB, więc możemy zapisać średnią wartość wektora Poyntinga w postaci
|
(27.12) |
Jeżeli natężenie pola E zmienia się sinusoidalnie to wartość średnia
, a stąd
|
(27.13) |
na tej podstawie
|
(27.14) |
Podstawiając dane otrzymujemy E0 = 0.13 V/m.
Wreszcie obliczamy pole B0
|
(27.15) |
Otrzymujemy wartość B0 = 4·10−10 T. Zauważmy jak małe jest pole magnetyczne.
Ten rozdział kończy moduł ósmy; możesz teraz przejść do podsumowania i zadań testowych.