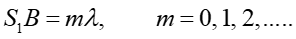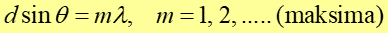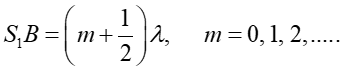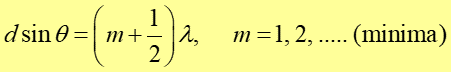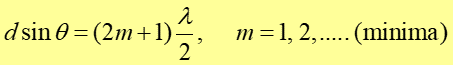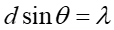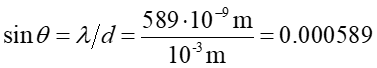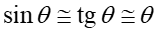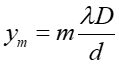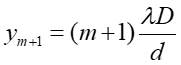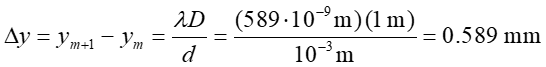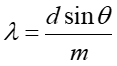29. Interferencja
• Spis treści  
• Spójność (koherencja) fal świetlnych  
•   Warunki stosowalności optyki geometrycznej

29.1 Doświadczenie Younga

  W rozdziale dotyczącym fal w ośrodkach sprężystych omawialiśmy nakładanie się (interferencję) fal. Doświadczenie wykonane, przez Younga (w 1801 r.) wykazało istnienie takiej interferencji dla światła. Był to pierwszy eksperyment wskazujący na falowy charakter światła.

W swoim doświadczeniu, Young oświetlił światłem słonecznym ekran, w którym był zrobiony mały otwór S₀. Przechodzące światło padało następnie na drugi ekran z dwoma szczelinami S₁ i S₂ i dalej rozchodziły się dwie, nakładające się na siebie fale kuliste tak jak na rysunku 29.1.

Warunki stosowalności optyki geometrycznej nie są spełnione i na szczelinach następuje ugięcie fal. Mamy do czynienia z optyką falową.

Jeżeli umieścimy ekran w jakimkolwiek miejscu, tak aby przecinał on nakładające się na siebie fale to możemy oczekiwać pojawienia się na nim miejsc ciemnych i jasnych następujących po sobie kolejno w zależności od wyniku nakładania się fal (rysunek 29.1). Miejsca ciemne powstają w wyniku wygaszania się interferujących fal, a jasne w wyniku ich wzajemnego wzmocnienia. Obserwujemy tak zwane prążki interferencyjne (rysunek 29.1).

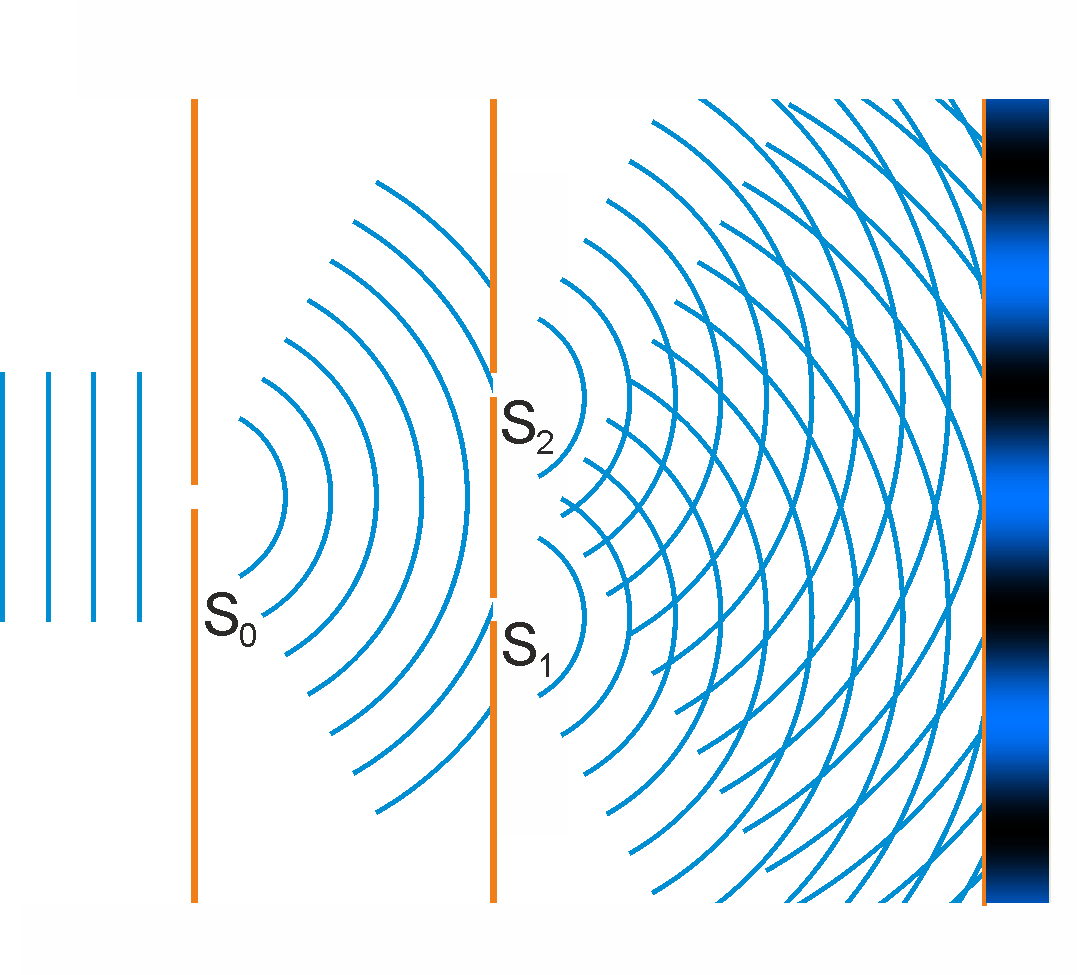
 Rys. 29.1. Schemat doświadczenia Younga

Przeanalizujemy teraz doświadczenie Younga ilościowo. Zakładamy, że światło padające zawiera tylko jedną długość fali (jest monochromatyczne). Na rysunku 29.2 poniżej punkt P jest dowolnym punktem na ekranie, odległym o r₁ i r₂ od wąskich szczelin S₁ i S₂.

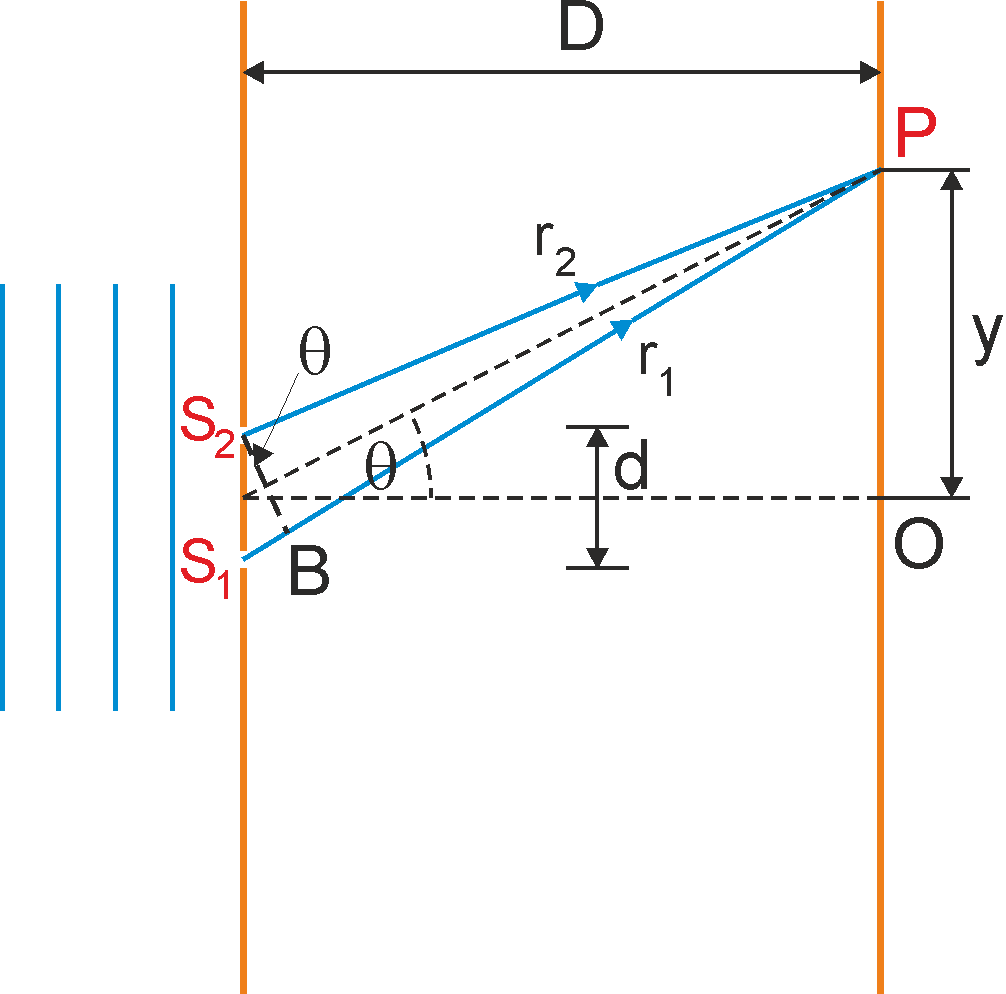
 Rys. 29.2. Interferencja, w punkcie P, fal wychodzących ze szczelin S₁ i S₂

Linia S₂B została poprowadzona tak, aby PS₂ = PB. Zwrócić uwagę, że dla przejrzystości na rysunku nie zachowano proporcji d/D. Naprawdę d << D i wtedy kąt S₁S₂B jest równy θ z dużą dokładnością.
Oba promienie wychodzące ze szczelin S₁ i S₂ są zgodne w fazie, gdyż pochodzą z tego samego czoła fali płaskiej. Jednak drogi, po których docierają do punktu P są różne więc i ich fazy w punkcie P mogą być różne. Odcinki PB i PS₂ są identyczne (tak to skonstruowaliśmy) więc o różnicy faz decyduje różnica dróg optycznych tj. odcinek S₁B. 
Aby w punkcie P wystąpiło maksimum natężenia światła, odcinek S₁B musi zawierać całkowitą liczbę długości fal. Jest tak dlatego, że po przebyciu odcinka równego λ faza fali powtarza się więc po przebyciu drogi równej mλ (m - liczba całkowita) fala ma fazę taką jak na początku tej drogi. Odcinek S₁B nie wpływa na różnicę faz, a ponieważ fale były zgodne w źródle więc będą zgodne w fazie w punkcie P.

Warunek na maksimum możemy zatem zapisać w postaci

Zgodnie z rysunkiem 29.2, więc

Zauważmy, że każdemu maksimum powyżej środkowego punktu O odpowiada położone symetrycznie maksimum poniżej punktu O. Istnieje też centralne maksimum opisywane przez m = 0.

Dla uzyskania minimum natężenia światła w punkcie P, odcinek S₁B musi zawierać połówkową liczbę długości fal, to jest

Przykład

Jako przykład rozpatrzmy dwie szczeliny odległe od siebie o 1 mm oświetlono żółtym światłem sodu o długości λ = 589 nm. Obliczymy odległość między sąsiednimi prążkami interferencyjnymi obserwowanymi na ekranie umieszczonym w odległości 1 m od szczelin.
Najpierw sprawdzamy położenie kątowe pierwszego maksimum. Dla m = 1 otrzymujemy

co daje θ ≈ 0.03°.

Dla tak małych kątów dobrym przybliżeniem jest

Z rysunku 29.2 wynika, że tgθ = y/D. Podstawiając to wyrażenie zamiast sinθ do równania (29.2) na maksimum interferencyjne otrzymujemy dla m-tego prążka

Odległość między nimi wynosi

Jeżeli θ jest małe to odległość między prążkami nie zależy od m, prążki są rozmieszczone na ekranie równomiernie. Jeżeli natomiast mamy fale o różnych długościach λ to powstaną oddzielne układy prążków (dla każdej z długości fal) o różnym odstępie między prążkami.

Równanie (29.2) opisujące położenie kątowe maksimów interferencyjnych może posłużyć do wyznaczenia długości fali

Tak właśnie Young wyznaczył długości fal światła widzialnego.