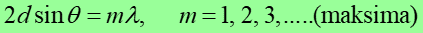30. Dyfrakcja
• Spis treści  
• Polaryzacja - Wstęp  
•   Interferencja fal z wielu źródeł, siatka dyfrakcyjna

30.6 Dyfrakcja promieni Roentgena (promieni X)

  W krystalicznych ciałach stałych atomy ułożone są w przestrzeni w sposób regularny tworząc tzw. sieć krystaliczną. Na rysunku 30.7 pokazane jest rozmieszczenie atomów w krysztale NaCl. Małe (niebieskie) kule przedstawiają atomy (jony) sodu, a duże (czerwone) jony chloru. Na rysunku pokazana jest tzw. komórka elementarna . Jest to najmniejsza jednostka (cegiełka), z której można zbudować kryształ.

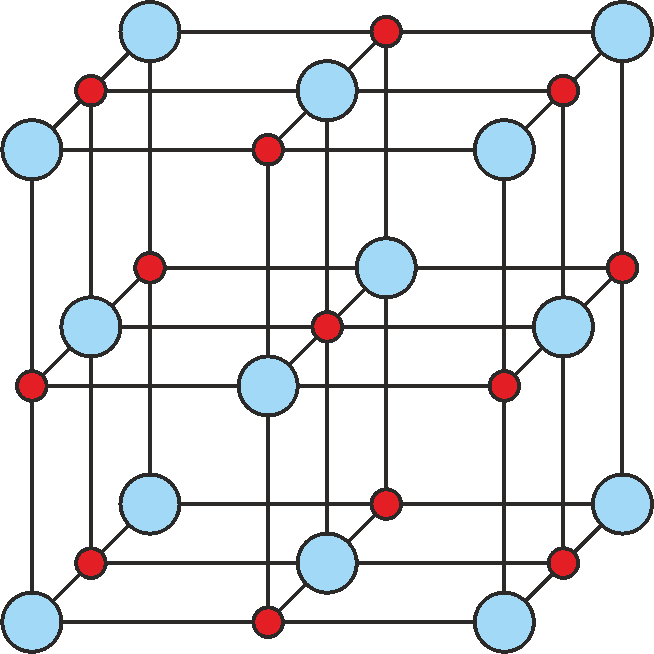
 Rys. 30.9. Rozmieszczenie jonów  w komórce elementarnej NaCl

Takie ułożenie atomów w powtarzający się regularny wzór powoduje, że krystaliczne ciało stałe stanowi naturalny, trójwymiarowy układ szczelin (przeszkód) czyli trójwymiarową siatkę dyfrakcyjną.

Jednak w tym przypadku światło widzialne jest bezużyteczne bo długość jego fal jest dużo większa od odległości między atomami λ >> a. Przykładowo, światło żółte ma długość równą 589 nm, a odległość między najbliższymi atomami w krysztale NaCl wynosi a ≈ 0.281 nm.

Musimy więc posłużyć się promieniowaniem X (promieniowanie rentgenowskie). Więcej o promieniowaniu rentgenowskim dowiemy się w dalszych rozdziałach, teraz zapamiętajmy jedynie, że jest to promieniowanie elektromagnetyczne o długościach fal rzędu 0.1 nm, tj. tego samego rzędu co odległości międzyatomowe w kryształach. Na rysunku 30.10 poniżej pokazana jest wiązka promieni X padająca na kryształ. Wiązki fal ugiętych na atomach padają na kliszę tworząc na niej w wyniku interferencji charakterystyczny obraz (układ punktów) zwany od nazwiska niemieckiego fizyka odkrywcy tej metody obrazem Lauego .

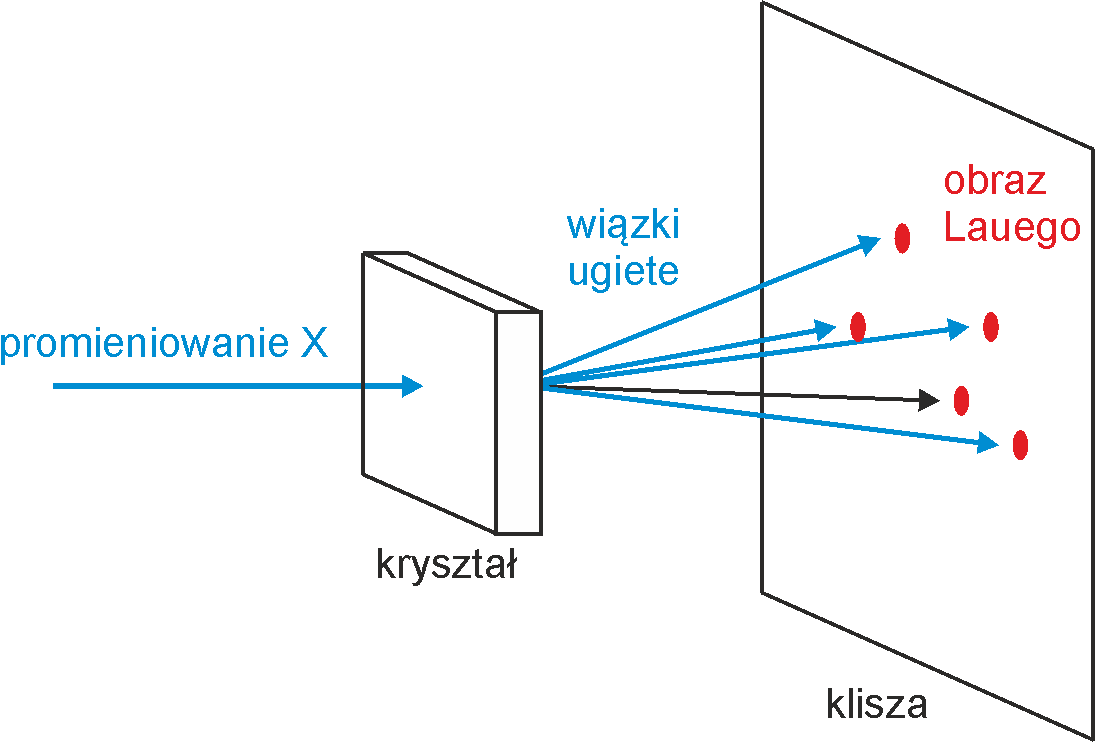
 Rys. 30.10. Ugięcie wiązki promieni X na krysztale

Natężenia linii w obrazie dyfrakcyjnym zależą od geometrii pojedynczej szczeliny. W idealnym przypadku zależą od szerokości szczeliny. Tak samo natężenia wiązek rozproszonych na krysztale zależą od geometrii pojedynczej rozpraszającej komórki elementarnej. Analiza położeń i natężeń tych punktów pozwala na określenie struktury kryształu.

Kierunki (kąty θ), dla których otrzymujemy wzmocnienie promieni X ugiętych na krysztale, określa prawo Bragga

gdzie d jest odległością między sąsiednimi płaszczyznami zawierającymi atomy, a θ kątem pomiędzy tymi płaszczyznami i padającym promieniowaniem.
 Więcej o ...  prawie Bragga.

Widzimy, że znając długość fali λ możemy z prawa Bragga wyznaczyć odległości międzyatomowe.
Dyfrakcja promieni X jest ważną metodą doświadczalną w badaniu ciała stałego.