31.4 Dwójłomność
Światło spolaryzowane można również uzyskać wykorzystując, występującą w pewnych kryształach, zależność współczynnika załamania światła od kierunku polaryzacji.
Dotychczas zakładaliśmy, że współczynnik załamania, nie zależy od kierunku rozchodzenia się
światła w ośrodku ani od jego polaryzacji. Ciała spełniające te warunki nazywamy ciałami optycznie
izotropowymi ![]() .
.
Istnieje jednak szereg ciał anizotropowych ![]() i dotyczy to nie tylko własności optycznych ale wielu innych. Na przykład
pewne kryształy łamią się łatwo tylko w jednej płaszczyźnie, a opór
elektryczny mierzony w różnych kierunkach jest różny, niektóre
kryształy łatwiej magnesuje się w jednym kierunku niż innych itd.
i dotyczy to nie tylko własności optycznych ale wielu innych. Na przykład
pewne kryształy łamią się łatwo tylko w jednej płaszczyźnie, a opór
elektryczny mierzony w różnych kierunkach jest różny, niektóre
kryształy łatwiej magnesuje się w jednym kierunku niż innych itd.
Na rysunku 31.7 poniżej pokazana jest niespolaryzowana wiązka światła padająca na kryształ kalcytu (CaCO3) prostopadle do jednej z jego ścian.
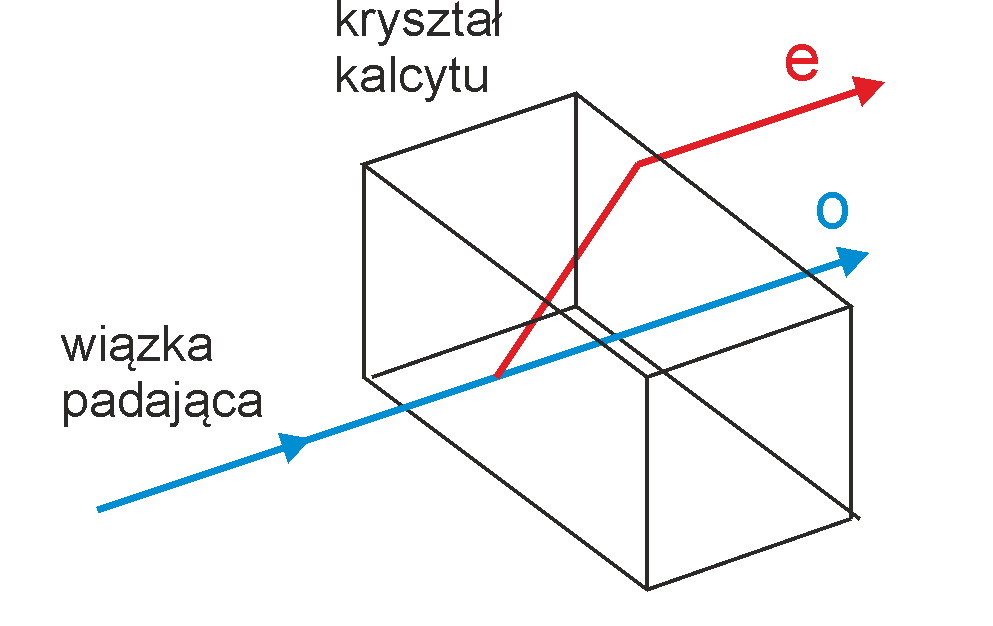
Rys. 31.7. Podwójne załamanie w krysztale kalcytu
Pojedyncza wiązka światła rozszczepia się, przechodząc przez kryształ, na dwa promienie. Mamy
do czynienia z dwójłomnością czyli,
podwójnym załamaniem ![]() .
.
Jeżeli zbadamy obie wychodzące wiązki za pomocą płytki polaryzującej to okaże się, że
obie wiązki są spolaryzowane liniowo, przy czym ich płaszczyzny drgań są wzajemnie prostopadłe.
Wiązki te noszą odpowiednio nazwy promienia zwyczajnego
(o) ![]() i promienia nadzwyczajnego (e)
i promienia nadzwyczajnego (e)
![]() .
.
Ponadto okazuje się, że promień zwyczajny spełnia prawo załamania (tak jak dla ośrodka izotropowego), a promień nadzwyczajny tego
prawa nie spełnia.
Zjawisko to tłumaczy się tym, że promień o przechodzi przez kryształ z jednakową prędkością
we wszystkich kierunkach (ma jeden współczynnik załamania no)
tak jak izotropowe ciało stałe, natomiast prędkość promienia e
zależy od kierunku w krysztale i zmienia się od wartości vo
do ve, a współczynnik załamania od no
do ne. Dla kalcytu no = 1.486,
a ne = 1.658. Wielkości ne i no
nazywamy głównymi współczynnikami załamania
![]() kryształu.
kryształu.
Niektóre podwójnie załamujące kryształy wykazują ponadto własność nazywaną
dichroizmem ![]() .
Kryształy te pochłaniają jeden z promieni (o lub e) silniej niż drugi. Na wykorzystaniu tego zjawiska opiera się działanie
szeroko stosowanych polaroidów.
.
Kryształy te pochłaniają jeden z promieni (o lub e) silniej niż drugi. Na wykorzystaniu tego zjawiska opiera się działanie
szeroko stosowanych polaroidów.
Ten rozdział kończy moduł dziewiąty; możesz teraz przejść do podsumowania i zadań testowych.


 Polaryzacja przez odbicie
Polaryzacja przez odbicie