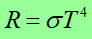32.2 Ciało doskonale czarne
Rozważmy pokazany na rysunku 32.2 blok metalowy posiadający pustą wnękę wewnątrz. W ściance bocznej tego bloku znajduje się niewielki otwór.
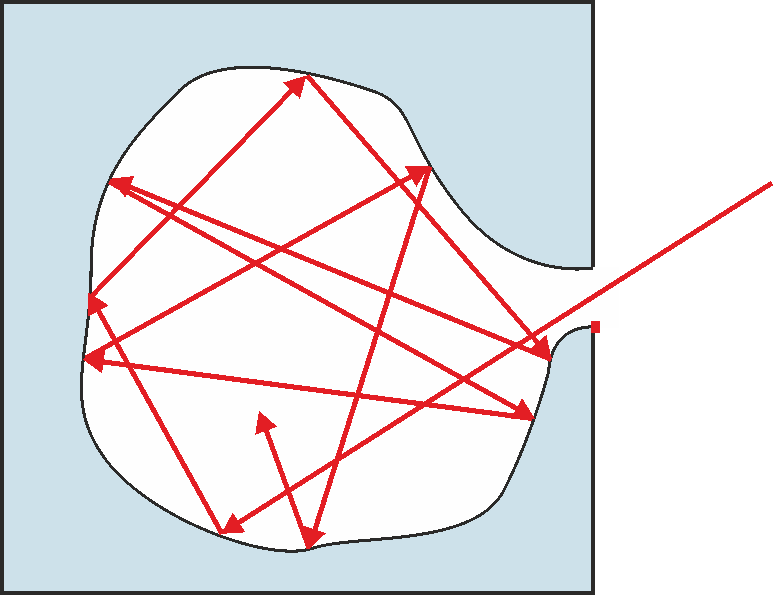
Rys. 32.2. Model ciała doskonale czarnego
Promieniowanie pada na otwór z zewnątrz i po wielokrotnych odbiciach od wewnętrznych ścian zostaje całkowicie pochłonięte. Oczywiście ścianki wewnętrzne też emitują promieniowanie, które może wyjść na zewnątrz przez otwór. Otwór wnęki ma więc własności ciała doskonale czarnego.
Z obserwacji światła wysyłanego przez takie ciało wynika, że:
- Promieniowanie wychodzące z wnętrza bloków ma zawsze większe natężenie niż promieniowanie ze ścian bocznych.
- Dla danej temperatury emisja promieniowania wychodzącego z otworów jest identyczna dla wszystkich źródeł promieniowania, pomimo że dla zewnętrznych powierzchni te wartości są różne.
|
Prawo, zasada, twierdzenie | Emisja energetyczna promieniowania ciała doskonale
czarnego (nie jego powierzchni) zmienia się wraz z temperaturą
według prawa Stefana-Boltzmanna
|
(32.2) |
gdzie σ jest uniwersalną stałą (stała Stefana-Boltzmanna) równą 5.67·10−8 W/(m2K4).
Zdolność emisyjna promieniowania Rλ dla ciała doskonale czarnego zmienia się z temperaturą tak jak na rysunku 32.3 poniżej.
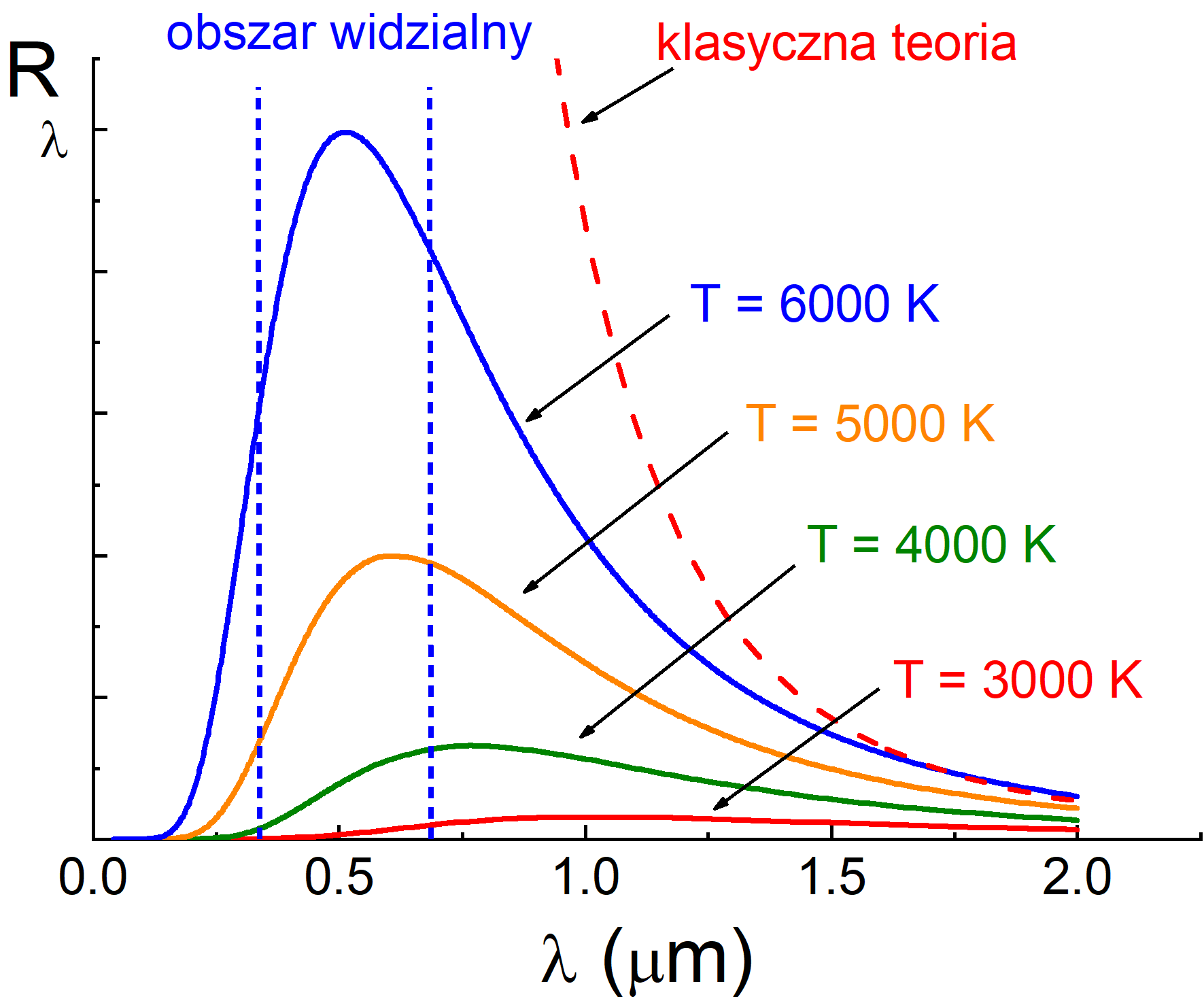
Rys. 32.3. Widmo promieniowania ciała doskonale czarnego w wybranych temperaturach
|
Prawo, zasada, twierdzenie Długość fali, dla której przypada maksimum emisji jest zgodnie z prawem Wiena odwrotnie proporcjonalna do temperatury ciała. |
|
Symulacje komputerowe Możesz prześledzić zależność widma promieniowania ciała doskonale czarnego od temperatury korzystając z programu komputerowego "Ciało doskonale czarne", dostępnego na stronie WWW autora i na stronie Open AGH. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera. |
Podkreślmy, że pokazane krzywe zależą tylko od temperatury i są całkiem niezależne od materiału oraz kształtu i wielkości ciała doskonale czarnego.
Żeby się o tym przekonać rozpatrzmy, pokazane na rysunku 32.4 dwa ciała doskonale czarne, tzn. dwie wnęki o dowolnym kształcie i jednakowej temperaturze ścianek obu wnęk (ciała stykają się). Promieniowanie oznaczone RA przechodzi z wnęki A do wnęki B, a promieniowanie RB w odwrotnym kierunku. Jeżeli te szybkości nie byłyby równe wówczas jeden z bloków ogrzewałby się a drugi stygł. Oznaczałoby to pogwałcenie drugiej zasady termodynamiki. Otrzymujemy więc RA = RB = RC gdzie RC opisuje całkowite promieniowanie dowolnej wnęki.
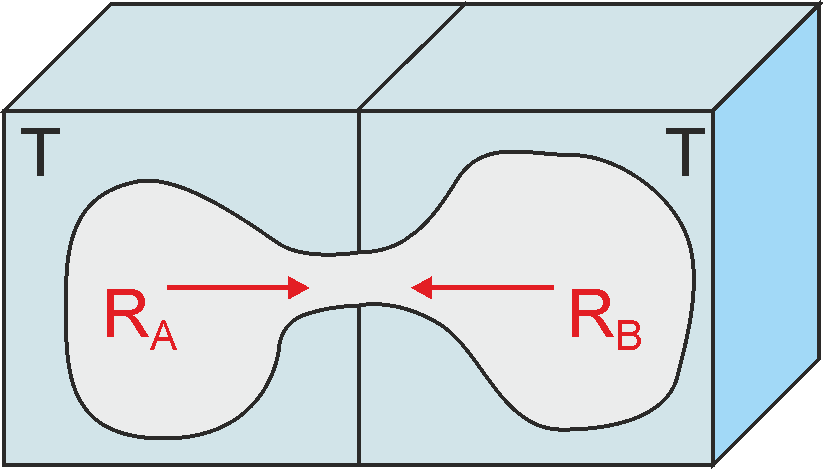
Rys. 32.4. Dwa ciała doskonale czarne o jednakowej temperaturze
Nie tylko energia całkowita ale również jej rozkład musi być taki sam dla obu wnęk. Stosując
to samo rozumowanie co poprzednio można pokazać, że
RλA = RλB
= RλC,
gdzie RλC oznacza widmową zdolność emisyjną dowolnej wnęki.


 Promieniowanie termiczne
Promieniowanie termiczne