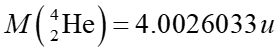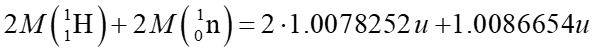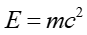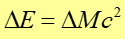38. Fizyka jądrowa
• Spis treści  
• Rozpady jądrowe  
•   Fizyka jądrowa - Wstęp

38.2 Oddziaływanie nukleon-nukleon

  Dotychczas poznane oddziaływania (grawitacyjne, elektromagnetyczne) nie pozwalają na wyjaśnienie struktury jądra atomowego. Aby wyjaśnić co tak silnie wiąże nukleony w jądrach atomowych trzeba wprowadzić nowe oddziaływanie. Ta siła wiążąca musi być większa niż siła odpychania elektrostatycznego występująca pomiędzy protonami. Określamy ją mianem siły jądrowej lub oddziaływania silnego .

Potencjał opisujący to oddziaływanie jest pokazany na rysunku 38.1 w porównaniu z potencjałem elektrostatycznego odpychania proton - proton.

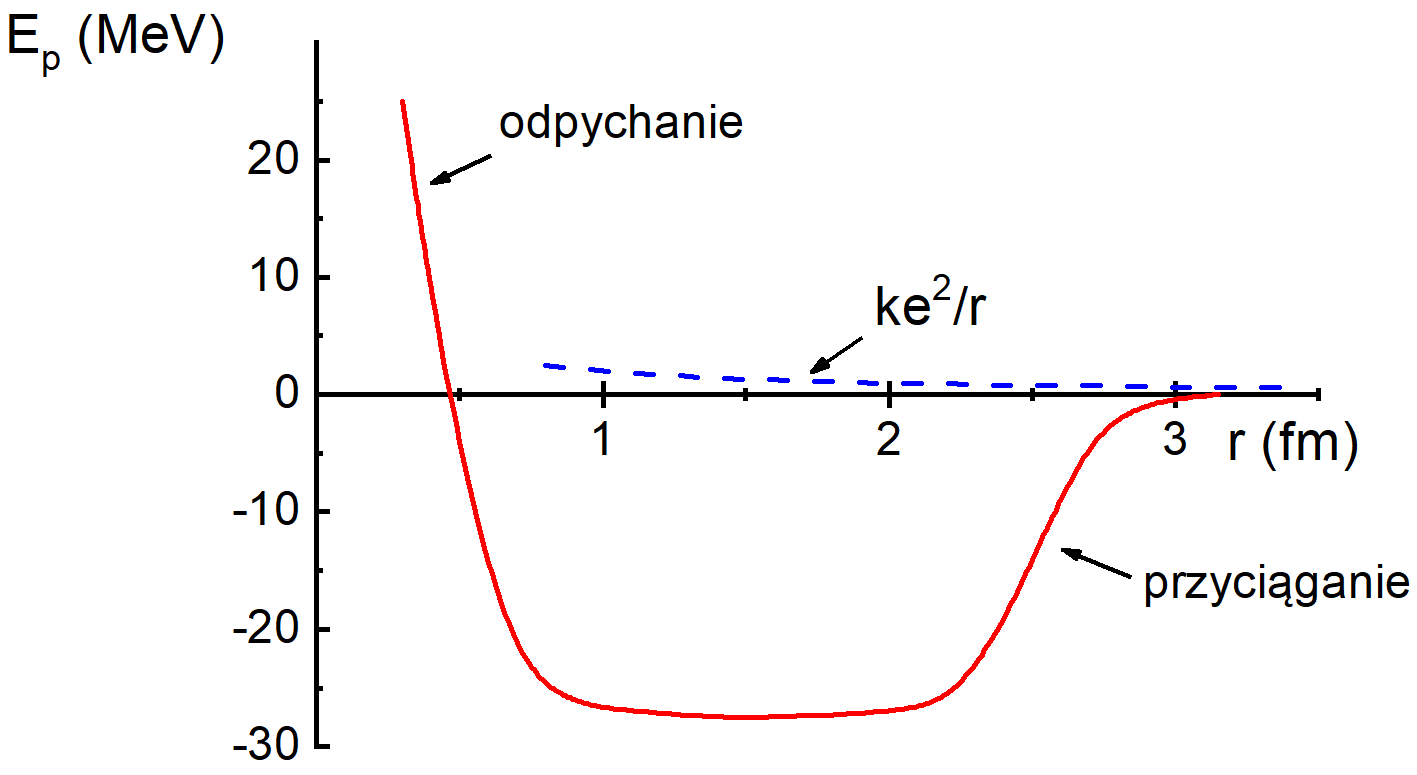
 Rys. 38.1 Energia potencjalna oddziaływania nukleon – nukleon (linia ciągła)
w porównaniu z energią odpychania proton – proton (linia przerywana)

Oddziaływanie proton - proton, proton - neutron i neutron - neutron jest identyczne (jeżeli zaniedbamy relatywnie małe efekty odpychania elektrostatycznego) i nazywamy go oddziaływaniem nukleon - nukleon.

Masy atomowe i energie wiązań można wyznaczyć doświadczalnie w oparciu o spektroskopię masową lub bilans energii w reakcjach jądrowych. W tabeli 38.1 poniżej zestawione są masy atomowe i energie wiązań ΔE jąder atomów wybranych pierwiastków.

Tab. 38.1.Masy atomowe i energie wiązań jąder atomów

	Z	A	Masa (u)	ΔE (MeV)	ΔE/A (MeV)
	0	1	1.0086654	-	-
	1	1	1.0078252	-	-
	2	4	4.0026033	28.3	7.07
	4	9	9.0121858	58.0	6.45
	6	12	12.0000000	92.2	7.68
	8	16	15.994915	127.5	7.97
	29	63	62.929594	552	8.50
	50	120	119.9021	1020	8.02
	74	184	183.9510	1476	8.02
	92	238	238.05076	1803	7.58

Analizując bliżej dane zestawione w tabeli 36.1 można uzyskać dalsze informacje o jądrach atomowych. Dla przykładu porównajmy masę atomu z sumą mas jego składników

Całkowita masa jego składników równa jest sumie mas dwu atomów wodoru  i dwu neutronów

Masy dwu elektronów są uwzględnione w masie helu jak i w masach dwóch atomów wodoru.

Zauważmy, że masa helu jest mniejsza od masy składników o wartość 0.0303779 u.

Analogiczny rachunek pokazuje, że dla każdego atomu jego masa jest mniejsza od masy składników o wielkość ΔM zwaną niedoborem masy lub defektem masy.

Wynik ten jest świadectwem istnienia energii wiązania jąder jak i równoważności masy i energii. Zauważmy, że energia nukleonów tworzących jądro zmienia się w miarę ich zbliżania od wartości E = 0 dla nukleonów swobodnych (r → ∞) do wartości ujemnej E < 0 dla nukleonów w jądrze (rysunek 38.1). Oznacza to, że gdy układ oddzielnych swobodnych nukleonów łączy się w jądro energia układu zmniejsza się o wartość ΔE energii wiązania jądra.

Zgodnie ze wzorem Einsteina całkowita energia spoczywającego jądra jest związana z jego masą zależnością (patrz uzupełnienie)

Oznacza to, że zmniejszeniu o ΔE całkowitej energii układu musi towarzyszyć, zgodnie z teorią względności, zmniejszenie masy układu o ΔM

Ćwiczenie Na podstawie zależności (38.5) oblicz energię wiązania dla  i porównaj uzyskaną wartość z danymi doświadczalnymi podanymi w tabeli 38.1. Skorzystaj z wyliczonego niedoboru masy dla ΔM = 0.0303779 u. Sprawdź obliczenia i wynik.

W ostatniej kolumnie tabeli 38.1 podana jest wielkość energii wiązania przypadającej na nukleon w jądrze ΔE/A. Jest to jedna z najważniejszych cech charakteryzujących jądro. Zauważmy, że początkowo wielkość ΔE/A wzrasta ze wzrostem liczby A, ale potem przybiera w przybliżeniu stałą wartość około 8 MeV. Wyniki średniej energii wiązania na nukleon w funkcji liczby masowej jądra A są pokazane na rysunku 38.2 poniżej.

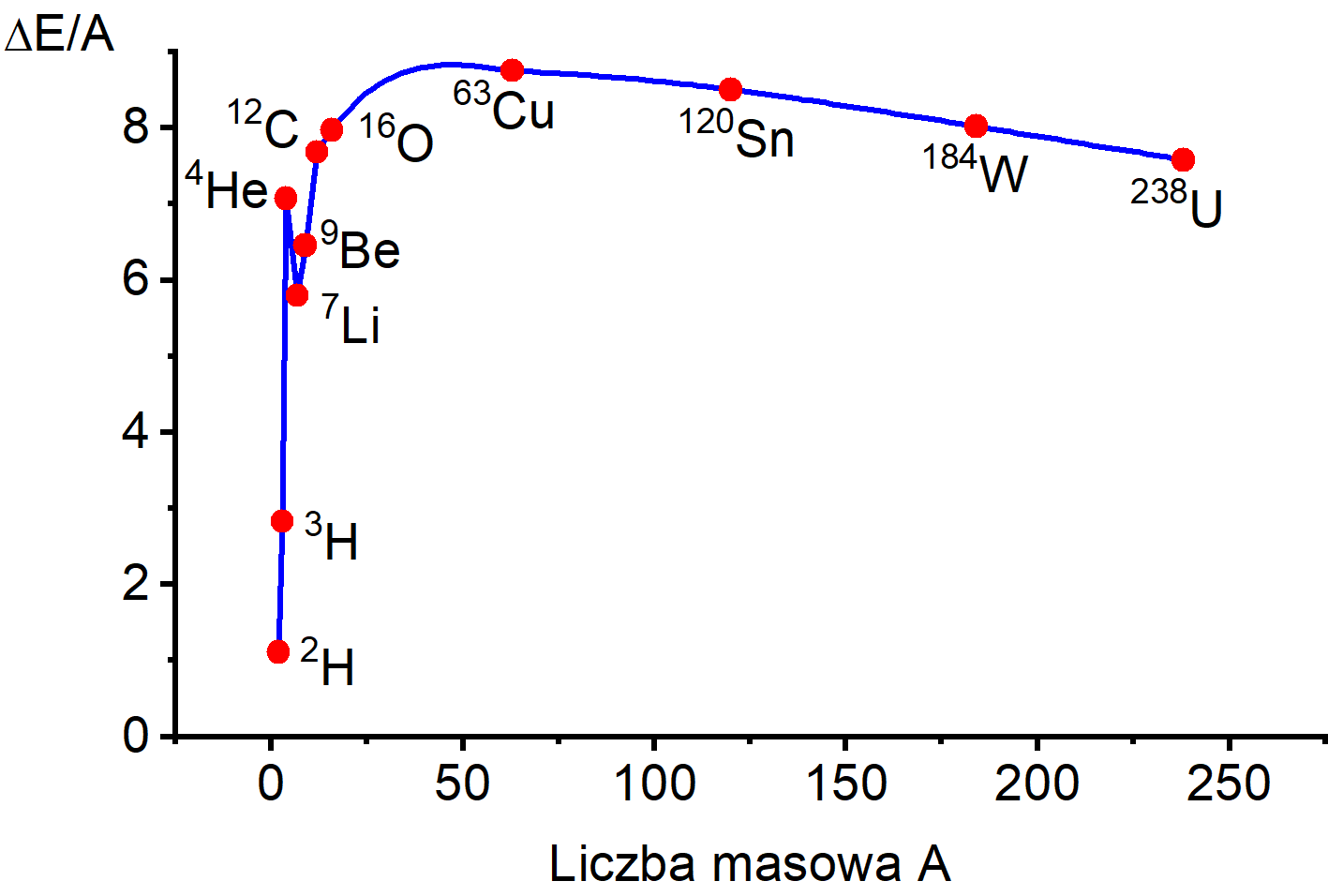
 Rys. 38.2 Energia wiązania na nukleon w funkcji liczby masowej A

Widzimy, że najsilniej są wiązane nukleony w jądrach pierwiastków ze środkowej części układu okresowego. Gdyby każdy nukleon w jądrze przyciągał jednakowo każdy z pozostałych nukleonów, to energia wiązania powinna zmieniać się jak liczba par nukleonów (liczba wszystkich wiązań), czyli proporcjonalnie do A². Wtedy wielkość ΔE/A powinna skalować się jak A. To, że tak nie jest dla A > 30 wynika głównie z krótkiego zasięgu sił jądrowych.