Całka krzywoliniowa nieskierowana.


Rozważmy łuk zwykły, otwarty, gładki L o równaniach parametrycznych

tÎ <a ,b >

i funkcję ¦ (x,y) określoną, ciągłą i ograniczoną na łuku L.

1o Biorę podział przedziału <a ,b >

D n = { t0 = a < t1< t2< .....<tn = b }

2o Podziałowi D n odpowiada podział łuku L na części punktami

{A0, A1, .... , An-1, An}

Ak =Ak (x(tk), y(tk)) (k=0, 1, 2, ... , n).

3o Biorę łuki częściowe (k=1, ... , n) i ich długości

| | = D Lk = (k=1, ... , n)

4o t k Î <tk-1, tk> k=1 , .... , n

Mk ( x(t k), y(t k) ) Î (k=1, ... , n)

5o Tworzę sumę całkową

 

DEF. Jeżeli dla każdego normalnego ciągu podziałów {D n} przedziału <a ,b > ciąg sum całkowych {Sn} jest zbieżny do tej samej granicy właściwej niezależnej od wyboru punktów Mk (t k) to tę granicę nazywamy całką krzywoliniową nieskierowaną funkcji f(x,y) po łuku L i oznaczamy symbolem

Interpretacja geometryczna.

1o Jeżeli f(x,y) = 1 całka
= | L | przedstawia długość łuku L.

2o Jeżeli f(x,y) jest ciągła i f(x,y) >0 to całka przedstawia pole części walcowej.

Interpretacja fizyczna.

Jeżeli r (x,y) jest gęstością liniową masy łuku L to

1o m(L)= - masa łuku L

2o Mx (L) = - moment statyczny łuku L względem osi Ox

My (L) = - moment statyczny łuku L względem osi Oy

3o Bx (L) = - moment bezwładności łuku L względem osi Ox

By (L) = - moment bezwładności łuku L względem osi Oy

4o S (x ,h ) – środek masy łuku L

x = h =

 

Twierdzenie. (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną).

Jeżeli funkcja f(x,y) jest ciągła na otwartym, zwykłym łuku gładkim L

t Î <a ,b >

to istnieje przy czym

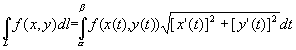
Przykład. Obliczyć współrzędne środka masy jednorodnego półokręgu L : x2 + y2 = R2 ,
y ³ 0 , ( r (x,y) = const = C).

t Î <0,p >

Mx (L) =

m (L) =

My (L) =

S (0, )

Gdy krzywa L = , Li – otwarte, gładkie łuki zwykłe .

W przypadku gdy łuk zwykły, otwarty, gładki L w R3 L: t Î <a ,b >

i f(x,y,z) jest ciągła na L to

.