DCałka powierzchniowa niezorientowana
Rozważmy przestrzeń
układu 0xyz.
Def. Gładkim punktem powierzchniowym (względem płaszczyzny 0xy) nazywamy wykres funkcji
z = f(x, y) ; (x, y) D
klasy 
w D gdzie D- obszar regularny domknięty o jednospójnym wnętrzu.
W analogiczny sposób określamy gładki punkt powierzchniowy względem płaszczyzny 0yz i 0xz.
Powierzchnie stanowiącą zbiór spójny punktów, którą można podzielić na skończoną liczbę gładkich punktów powierzchniowych nazywamy powierzchnią regularną,
Rozważmy gładki punkt powierzchniowy S orównaniu
z = f(x, y) ; (x, y) D
oraz funkcję F (x, y, z) określoną i ciągłą na tym płacie
Biorę podział obszaru D na n obszarów regularnych.
= {
,…,
}
= średnica obszaru 
= d (
,
)
,
= max- Srednica podziału
podziałowi odpowiada podział płata S
{
,…,
}
pole punkta powierzchni 
= |
|= 
; (k=1,…,n)
punktowi
odpowiada punkt 
(k=1,…,n)
tworzę sumę całkową 
Rzutem na płaszczyzne 0xy jest
Rzutem na płaszczyzne 0xy jest
Def. Ciąg podziałów {
} obszaru D jest normalny <=> 
Def. Jeżeli dla każdego normalnego ciągu podziałów {
} obszaru D ciąg sum całkowych {
}jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów to tą granicę nazywamy całką powierzchniową niezorientowaną funkcji F (x, y, z) po płacie gładkim S i oznacza się symbolem:
Interpretacja geometryczna
Jeżeli F (x, y, z)
1 to 
- pole punkta gładkiego S.
Interpretacja fizyczna
Jeżeli
jest gęstością powierzchniową masy punkta S to
=m(S) – masapunkta S.
Inne zastosowanie:
, S(
) , 
, 
, 
Twierdzenie (o zamianie całki powierzchniowej niekierowanej na całkę podwójną)
Jeżeli funkcja F (x, y, z) jest ciągła na gładkim płacie S:
z= f(x,y) , (x,y)
D to istnieje i
(*)=
Jeżeli S jest powierzchnią regularną
i
- gładkie punkty powierzchni względem płaszczyzn 0xy v 0yz v 0xz.
Wtedy = 
Przykład
Obliczyć
=
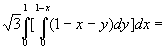
S : 
- kąt o wierzchołkach A(1,0,0) , B(0,1,0) , C(0,0,1)
S: x+y+z = 1 <=> z = 1-x-y , gdzie:
S: x+y+z=1 , D = {(x,y) : 0 
x
1 ; 0y1-x}
=
=
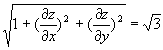
Przykład 2
Obliczyć pole płata S powierzchni z = xy którego rzutem na płaszczyznę 0xy jest koło
Xy > 0
|S| = 4
4
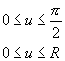
Przykład
Znaleźć masę powierzch. kuli, jeżeli gęstość tej powierzch.w każdym punkcie jest liczbowo równa odległość tego punktu od pewnej określonej średnicy.
Średnica np. oś
0z
, 
m(S) = 2m 
= 2R
= 
= 
= 
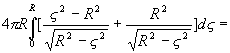
Wyznaczyć środek ciężkości połowy powierzchni kuli
, bo 
Przykład
Obliczyć
S – boczna powierzchnia walca ograniczonego powierzchnią walcową
i płaszcz. z = 0 , z = H
S: 
, 
= 
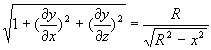