1. Пример программы МКЭ
Данный пример является переводом на русский язык соответствующей главы книги
A. Milenin Podstawy MES. Zagadnienia termomechaniczne, Wydawnictwo AGH, Kraków, 2010.
(А. Миленин Основы МКЭ. Термомеханические задания. Издательство АГХ, Краков, 2010)
www
1.1. Формулировка проблемы
Рассмотрим задачу нестационарного теплообмена. Систему уравнений МКЭ получаем с помощью следующего выражения:
![]() , (6.8)
, (6.8)
где:
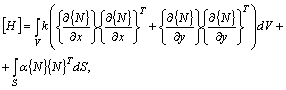 (5.14)
(5.14)
![]() , (5.15)
, (5.15)
![]() . (6.3)
. (6.3)
В уравнениях (6.8) {t1} - узловые значения температуры в момент времени
![]() , {t0} - узловые
значения температуры в момент времени
, {t0} - узловые
значения температуры в момент времени ![]() .
.
1.2. исходные данные
Пример исходных данных на рисунке 9.1.
100 mTbegin Начальная температура, C
1000 mTime Время процесса, s
1 mdTime Шаг по времени, s
1200 mT_otoczenia Температура окружающей среды C
300 mAlfa Коэффициент теплообмена W/Cm2
100 mH0 Высота сечения, mm
100 mB0 Ширина сечения, mm
25 mNhH Число узлов по высоте
25 mNhH Число узлов по ширине
700 mC Теплоемкость, J/Ckg
25 mK Теплопроводность
7800 mR Плотность kg/m3
Rys. 9.1. Пример содержания файла с исходными данными
1.3. Текст программы
Программа написана на языке FORTRAN90. Использован компилятор Intel. Полный текст можно скачать с адреса http://home.agh.edu.pl/~milenin/programs/.
1.3.1. Главная программа TEMP2D
Код главной программы TEMP2D показан на rys. 9.2. Обозначения главных переменных следующие:
GlobData – Название модуля с главными (глобальными) переменными;
dTauMax – Максимально допустимый шаг по времени;
n, Ntau – Номер шага по времени и число этх шагов;
Главные процедуры:
IniEL4 – инициализация данных для выбранного конечного элемента (выбранный тип: 4- узловой элемент);
InpData – считывание исходных данных;
GenGrid2d – генерация сетки КЭ;
ALLOCATE_Matrix – выделение памяти для массивов;
SOLVER – решение для текушего шага по времени.
program TEMP2D
!*************************************************************************
! PROGRAM: TEMP2D
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
!************************************************************************
use GlobData;
implicit none
real*8 :: Asr,dTauMax,TauP;
integer*4 :: n, Ntau, i, iErr;
call IniEL4();
call InpData();
call GenGrid2d(mH0,mB0,mNhH,mNhB, mGr);
call SetControlPoints();
CALL ALLOCATE_Matrix();
CALL WriteControlPointsBegin();
Asr = mK / (mC * mR);
mdTime = DBLE(mB0/(1e3*mNhB))**2/(0.5*Asr);
CALL WriteControlPoints();
Ntau = int(mTime/mdTime)+1;
mdTime = mTime/DBLE(Ntau);
mTau = 0;
do n=1, Ntau
mTau = mTau + mdTime;
CALL SOLVER( );
CALL WriteControlPoints();
end do;
CLOSE(88); CLOSE(89);
DEALLOCATE ( mA, STAT=iErr );
DEALLOCATE ( mB, STAT=iErr );
DEALLOCATE ( mX, STAT=iErr );
end program TEMP2D
Rys. 9.2. Главная программа TEMP2D
1.3.2. Структуры данных и глобальные переменные
Правильно спроектированные структуры данных снижают вероятность ошибки и упрощают расчет. Ниже приведен пример таких структур.
На rys. 9.3 показан код модуля My_typ с определением структур данных. Описаны следующие структуры:
Node – структура данных, содержащая информацию о узлах КЭ сетки: x, y – координаты узла, t – температура в узле, CR – скорость измерения температуры;
Element – структура данных, содержащая информацию об элементе сетки МКЭ: nop – номера узлов, которые входят в состав элемента, Npov – число поверхностей КЭ, которые контактирут с окружающей средой; aPov – локальные номера контактных поверхностей элемента.
gr2d – структура, содержащая сетку КЭ: nh – число узлов; ne – число КЭ; nbn – число узлов в используемом КЭ; ncn – число степеней свободы в одном КЭ, для тепловой задачи равна nbn; nhPov – число узлов сетки КЭ, находящихся на поверхности контакта с окружающей средой; EL – массив длины ne содержащий данные типа typu Element для каждого КЭ сетки; ND – массив длиной nh содержащий данные типа Node для каждого узла сетки.
cor_L – структура данных, содержащая локальные координаты N, E точки в объеме элемента.
Gran – структура данных, содержащая информацию о поверхностях используемого конечного элемента: N_p – число точек интегрирования по поверхности; P – массив структур типа cor_L длиной N_p содержащий локальные координаты точек интегрирования Гаусса; W – массив длиной N_p содержащий веса точек интегрирования в соответствии; Nf – массив длиной nbn содержащий значения функций формы, расчитанные в точках интегрирования на поверхности элемента; N1,N2 – массивы длиной nbn содержащие значения производных функций формы по локальным переменным, расчитанные в точках интегрирования на поверхности элемента; UZEL – локальные номера узлов поверхности.
ELEM – структура данных, содержащая данные об используемом конечном элементе: nbn – число узлов в элементе, nbnp – число узлов, используемых для интерполяции среднего напряжения (используется в задаче теории пластичности), N_p – число точек интегрирования в объеме элемента; Nf – массив рзмером nbn содержащий значения функций формы в точках инрегрирования в объеме элемента; N1, N2 – массивы длиной nbn содержащие значения производных функций формы по локальным переменным, расчитанные в точках интегрирования в объеме конечного элемента; P – массив структур типа cor_L длиной N_p содержащий координаты точек интегрирования Гаусса в объеме элемента в локальной системе координат; L – массив структур типа cor_L длиной N_p содержащий локальные координаты узлов элемента; W – массив длиной N_p содержащий веса точек интегрирования Гаусса в объеме элемента; Sf – массив длиной, равной максимальному количеству поверхностей используемого конечного элемента (в примере равна 4), содержащий переменные типа Gran.
module My_typ;
! ******************************************************************
! Typy danych
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
implicit none;
type node
real*8 :: x,y,t,CR;
integer*4 :: status;
end type
type element
integer*4 :: nop(4);
integer*4 :: Npov; ! Liczba kontaktowych powierzchni elementu 0-1-2
integer*4 :: aPov(2); ! Lokalne numery kontaktowych powierzchni elementu
end type
type gr2d
integer*4 :: nh, ne, nbn, ncn, nhPov;
type(element) , dimension(:), pointer :: EL;
type(node) , dimension(:), pointer :: ND;
end type
type cor_L;
real*8 N, E;
end type cor_L;
type Gran
integer*4 :: N_p; ! Liczba punktów całkowania po powierzchni grani
type(cor_L), dimension(:), pointer :: P;
real*8, dimension(:), pointer :: W;
real*8, dimension(:,:), pointer :: N1,N2,Nf; ! N1(nbn,N_p)
integer*1, dimension(:),pointer :: UZEL;
! Lokalne numery węzłów grani
end type Gran;
type ELEM;
integer*4 :: nbn, nbnp, N_p;
real*8, dimension(:,:), pointer :: N1,N2,Nf; ! N1(nbn,N_p)
type(cor_L), dimension(:), pointer :: P; ! P(N_p)
type(cor_L), dimension(:), pointer :: L; ! Współrzędne węzłów elementu
real*8, dimension(:), pointer :: W; ! Waga punktów całkowania W(N_p)
type(Gran) :: Sf(4);
end type ELEM;
end module My_typ;
Rys. 9.3. Используемые типы данных
Модуль GlobData содержит определение глобальных переменных, доступ к этим переменным: use GlobData. Содержание модуля на rys. 9.4.
module GlobData;
! ******************************************************************
! Globalne zmianne
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
use My_typ;
implicit none;
real*8 :: mTbegin; ! Начальная температура
real*8 :: mTime; ! Время процемма
real*8 :: mdTime; ! Шаг по времени
real*8 :: mTau; ! Текущее время
real*8 :: mT_otoczenia; ! Температура окружающей среды
real*8 :: mAlfa; ! Коэффициент теплообмена
real*8 :: mH0; ! Высота сечения
real*8 :: mB0; ! Ширина сечения
integer*4 :: mNhH; ! Число узлов по высоте
integer*4 :: mNhB; ! Число узлов по ширине
integer*4 :: mLDA; ! Ширина ленты матрицы жесткости
real*8 :: mC; ! Теплоемкость
real*8 :: mK; ! Коэффициент теплопроводности
real*8 :: mR; ! плотность
type(gr2d) :: mGr; ! Сетка МКЭ
type(ELEM) :: mEL4; ! Данные используемого КЭ
integer*4 :: mContrPoints(9); ! Контрольные точки
REAL*8 :: mcpX(9),mcpY(9);
real*8, dimension(4,4) :: est; ! Матрица жесткости текущего элемента
real*8, dimension(4) :: r; ! Вектор нагрузок текущего КЭ
real*8, dimension(:), allocatable :: mB; ! Глобальный вектор нагрузок
real*8, dimension(:,:), allocatable :: mA; ! Глобальная матрица жесткости
real*8, dimension(:), allocatable :: mX; ! Глобальный вектор неизвестных
end module GlobData;
Rys. 9.4. Глобальные переменные
1.3.3. Процедура инициализации данных для элемента
Заполнение переменной mEL4 типа ELEM происходит в программе IniEL4 показанной на rys. 9.5. В первой части программы задается число узлов элемента nbn равное 4. Выбранная схема интегрирования содержит 4 точки, поэтому задано N_p=4. Выделяется память массивам N1, N2, Nf, P, W и L. Далее заполняются локальные координаты точек интегрирования Гаусса. В каждой точке интегрирования расчитываются величины N1, N2 i Nf.
Аналогично заполняются структуры для поверхностей элементов. При использовании иного типа КЭ необходимо соответствующим образом изменить переменную mEL4 и сетку КЭ.
SUBROUTINE IniEL4();
! ******************************************************************
! Inicjalizacja danych dla elementu
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
use GlobData;
implicit none;
REAL*8 :: Alfa,L1,L2,e,n,SN;
integer*4 :: iP,i;
Alfa = 1/(sqrt(3.0));
mEL4%nbn=4;
mEL4%N_p=4;
ALLOCATE(mEL4%N1( mEL4%nbn, mEL4%N_p ));
ALLOCATE(mEL4%N2( mEL4%nbn, mEL4%N_p ));
ALLOCATE(mEL4%Nf( mEL4%nbn, mEL4%N_p ));
ALLOCATE(mEL4%P ( mEL4%N_p ));
ALLOCATE(mEL4%W ( mEL4%N_p ));
ALLOCATE(mEL4%L ( mEL4%nbn ));
mEL4%W = 1.0;
mEL4%P(1)%E = -Alfa;
mEL4%P(1)%N = -Alfa;
mEL4%P(2)%E = Alfa;
mEL4%P(2)%N = -Alfa;
mEL4%P(3)%E = Alfa;
mEL4%P(3)%N = Alfa;
mEL4%P(4)%E = -Alfa;
mEL4%P(4)%N = Alfa;
mEL4%L(1)%E = -1;
mEL4%L(1)%N = -1;
mEL4%L(2)%E = 1;
mEL4%L(2)%N = -1;
mEL4%L(3)%E = 1;
mEL4%L(3)%N = 1;
mEL4%L(4)%E = -1;
mEL4%L(4)%N = 1;
DO iP = 1, mEL4%N_p
L1 = mEL4%P(iP)%E
L2 = mEL4%P(iP)%N
mEL4%Nf(1,iP) = 0.25*(1-L1)*(1-L2);
mEL4%N1(1,iP) = -0.25*(1-L2);
mEL4%N2(1,iP) = -0.25*(1-L1);
mEL4%Nf(2,iP) = 0.25*(1+L1)*(1-L2);
mEL4%N1(2,iP) = 0.25*(1-L2);
mEL4%N2(2,iP) = -0.25*(1+L1);
mEL4%Nf(3,iP) = 0.25*(1+L1)*(1+L2);
mEL4%N1(3,iP) = 0.25*(1+L2);
mEL4%N2(3,iP) = 0.25*(1+L1);
mEL4%Nf(4,iP) = 0.25*(1-L1)*(1+L2);
mEL4%N1(4,iP) = -0.25*(1+L2);
mEL4%N2(4,iP) = 0.25*(1-L1);
end do;
DO i = 1, 4
mEL4%Sf(i)%N_p = 2;
ALLOCATE( mEL4%Sf(i)%P( mEL4%Sf(i)%N_p ) );
ALLOCATE( mEL4%Sf(i)%W( mEL4%Sf(i)%N_p ) );
mEL4%Sf(i)%W = 1;
ALLOCATE( mEL4%Sf(i)%N1( mEL4%nbn, mEL4%Sf(i)%N_p));
ALLOCATE( mEL4%Sf(i)%N2( mEL4%nbn, mEL4%Sf(i)%N_p));
ALLOCATE( mEL4%Sf(i)%Nf( mEL4%nbn, mEL4%Sf(i)%N_p));
ALLOCATE( mEL4%Sf(i)%UZEL( 2 ) );
END DO;
mEL4%Sf(1)%UZEL(1) = 4; mEL4%Sf(1)%UZEL(2) = 1;
mEL4%Sf(2)%UZEL(1) = 1; mEL4%Sf(2)%UZEL(2) = 2;
mEL4%Sf(3)%UZEL(1) = 2; mEL4%Sf(3)%UZEL(2) = 3;
mEL4%Sf(4)%UZEL(1) = 3; mEL4%Sf(4)%UZEL(2) = 4;
mEL4%Sf(1)%P(1)%N=Alfa; mEL4%Sf(1)%P(1)%E=-1;
mEL4%Sf(1)%P(2)%N=-Alfa; mEL4%Sf(1)%P(2)%E=-1;
mEL4%Sf(2)%P(1)%N=-1; mEL4%Sf(2)%P(1)%E=-Alfa;
mEL4%Sf(2)%P(2)%N=-1; mEL4%Sf(2)%P(2)%E=Alfa;
mEL4%Sf(3)%P(1)%N=-Alfa; mEL4%Sf(3)%P(1)%E=1;
mEL4%Sf(3)%P(2)%N=Alfa; mEL4%Sf(3)%P(2)%E=1;
mEL4%Sf(4)%P(1)%N=1; mEL4%Sf(4)%P(1)%E=Alfa;
mEL4%Sf(4)%P(2)%N=1; mEL4%Sf(4)%P(2)%E=-Alfa;
do i = 1, 4
DO iP = 1, 2
e = mEL4%Sf(i)%P(ip)%E;
n = mEL4%Sf(i)%P(ip)%N;
mEL4%Sf(i)%Nf(1,ip) = 0.25*(1-e)*(1-n);
mEL4%Sf(i)%Nf(2,ip) = 0.25*(1+e)*(1-n);
mEL4%Sf(i)%Nf(3,ip) = 0.25*(1+e)*(1+n);
mEL4%Sf(i)%Nf(4,ip) = 0.25*(1-e)*(1+n);
mEL4%Sf(i)%N1(1,ip) = -0.25*(1-n);
mEL4%Sf(i)%N1(2,ip) = 0.25*(1-n);
mEL4%Sf(i)%N1(3,ip) = 0.25*(1+n);
mEL4%Sf(i)%N1(4,ip) = -0.25*(1+n);
mEL4%Sf(i)%N2(1,ip) = -0.25*(1-e);
mEL4%Sf(i)%N2(2,ip) = -0.25*(1+e);
mEL4%Sf(i)%N2(3,ip) = 0.25*(1+e);
mEL4%Sf(i)%N2(4,ip) = 0.25*(1-e);
END DO;
end do;
END SUBROUTINE IniEL4; (а)
 (б)
(б)
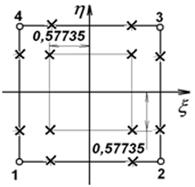
Rys. 9.5. Инициализация данных для КЭ (а) и используемый КЭ (б)
1.3.4. Процедура считывания исходных данных и выделения памяти массивам
Текст программы на rys. 9.6. Программа открывает текстовый файл indata.t2d, структура которого описана выше.
Subroutine InpData();
! ******************************************************************
! Wczytywanie danych
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
use GlobData;
implicit none;
integer nFile,i,j,iost;
nFile = 89
OPEN (nFile, FILE='indata.t2d', action='read')
read(nFile, *);
read(nFile, *);
read(nFile, *);
read(nFile, *);
read(nFile, *) mTbegin;
read(nFile, *) mTime;
read(nFile, *) mdTime;
read(nFile, *) mT_otoczenia;
read(nFile, *) mAlfa;
read(nFile, *) mH0;
read(nFile, *) mB0;
read(nFile, *) mNhH;
read(nFile, *) mNhB;
read(nFile, *) mC;
read(nFile, *) mK;
read(nFile, *) mR;
close (nFile);
end Subroutine InpData
Rys. 9.6. Программа считывания данных.
Выделение памяти для матрицы жесткости начинается расчетом ширины полосы ненулевых элементов mLDA, затем выделется память матрице жесткости mA, вектору неизвестных mX и ветору нагрузок mB. В методических целях показан также вариант выделения памяти для полной матрицы жесткости размером nh*nh.
SUBROUTINE ALLOCATE_Matrix;
use GlobData;
implicit none;
integer*4 :: NEL, i, j, ii, jj, jB, nk(4),NeMaxB, ierr;
mLDA=0;
do NEL = 1,mGr%ne
do i=1,mEL4%nbn
nk(i) = mGr%EL(NEL)%nop(i);
end do;
do i=1,mEL4%nbn
! * ii - wiersz *
ii=nk(i);
do j=1,mEL4%nbn
! * jj - kolumna *
jj=nk(j);
jB = jj-ii+1;
if(jB>=mLDA) then
mLDA=jB;
NeMaxB = NEL;
end if;
end do;
end do;
end do;
ALLOCATE ( mA(mLDA, mGr%nh), STAT=iErr );
! ALLOCATE ( mA(mGr%nh, mGr%nh), STAT=iErr );
! Pelna matryca MES
ALLOCATE ( mB(mGr%nh), STAT=iErr );
ALLOCATE ( mX(mGr%nh), STAT=iErr );
END SUBROUTINE ALLOCATE_Matrix
Rys. 9.7. Программа расчета и выделения памяти массивам.
1.3.5. Процедура решения задачи на текущем шаге по времени
Текст программы представлен на rys. 9.8.
SUBROUTINE SOLVER( );
! ******************************************************************
! Solver
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
use GlobData;
use msimsl;
implicit none;
integer*4 :: NEL;
integer*4, dimension(4) :: nk;
integer*4 :: jB,iB,NeMaxB,NCODA,i,j,ii,jj;
integer*4 :: iErr;
mA=0; mB=0; mX=0;
do NEL=1, mGr%ne
do i=1, mEL4%nbn
nk(i) = mGr%EL(NEL)%nop(i);
end do;
CALL FeSM_heat( NEL );
do i=1, mEL4%nbn
ii = nk(i); ! wiersz w macierzy pełnej
do j=1, mEL4%nbn
jj = nk(j); ! Kolumna w macierzy pełnej
iB = mLDA + ii - jj;! Wiersz w macierzy pasmowej
if ((jj>=ii).AND.(iB<=mLDA)) then
mA(iB, jj) = mA(iB, jj) + est(i,j); ! Wypełnienie macierzy pasmowej
end if;
! mA(ii,jj) = mA(ii,jj) + est(i,j); ! Wypełnienie macierzy pełnej
end do;
mB(ii) = mB(ii) + r(i);
end do;
end do;
NCODA = mLDA-1;
CALL DLSAQS (mGr%nh, mA, mLDA, NCODA, mB, mX)
! Program do rozwiązania układu równań z macierzą pasmową
! NCODA=1;
! CALL DLSARG (mGr%nh, mA, mGr%nh, mB, NCODA, mX)
! Program do rozwiązania układu równań z macierzą pełną
do i=1, mGr%nh
mGr%nd(i)%CR = ( mGr%nd(i)%t-mX(i) ) / mdTime;
mGr%nd(i)%t = mX(i);
end do;
END SUBROUTINE SOLVER;
Rys. 9.8. Программа заполнения глобальной матрицы жесткости и решения системы уравнений
В данной программе использованы следующие обозначения:
NEL – текущий номер конечного элемента;
Nk – массив, содержащий номера узлов, образующий данный элемент;
FeSM_heat – программа расчета матрицы жесткости и вектора нагрузок текущего элемента NEL;
DLSAQS – программа решения систебу уравнений с ленточной матрицей;
DLSARG – программа решения системы уравнений с полной матрицей.
1.3.6. Программа расчета матрицы жесткости и вектора нагрузок текущего элемента
Программа FeSM_heat (rys. 9.9) состоит из двух частей:
PRE_heat_mat – расчет матрицы и вектора нагрузок;
PRE_heat_pov_mat – учет граничных условий.
SUBROUTINE FeSM_heat( NEL );
! ******************************************************************
! Generacja macierzy elementu NEL
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ******************************************************************
use GlobData;
implicit none;
integer*4 :: NEL; ! Numer bieżącego Elementu
est = 0;
r = 0;
call PRE_heat_mat( NEL );
call PRE_heat_pov_mat(NEL );
END SUBROUTINE FeSM_heat;
Rys. 9.9. Расчет матрицы жесткости текущего КЭ (NEL)
Текст программы PRE_heat_mat показано на rys. 9.10. Программа Jacob_2d расчитывает матрицу Якоби, обратную ей матрицу и определитель матрицы якоби в каждой точке Гаусса.
subroutine PRE_heat_mat( NEL );
use GlobData;
implicit none;
integer*4 :: NEL;
INTEGER*4 :: I,j,N,P,Id;
REAL*8, DIMENSION(2,2) :: J_,J_inv; ! Macierz Jakobiego i macierz odwrotna
REAL*8 :: DetJ,Ni,Nn,Hin,Cin;
real*8 :: T0p;
REAL*8, DIMENSION(4) :: Ndx,Ndy; ! Pochodne funkcji kształtu względem X i Y
REAL*8, DIMENSION(4) :: X,Y,Temp_0;
DO I=1,mEL4%NBN
Id = ABS( mGr%EL(NEL)%NOP(I) );
X(I) = mGr%nd(Id)%x /1000.0; ! [m]
Y(I) = mGr%nd(Id)%y /1000.0; ! [m]
Temp_0(i)= mGr%nd(Id)%t;
END DO
DO P=1, mEL4%N_p
CALL Jacob_2d(J_, J_inv, P, mEL4%N_p, mEL4%NBN, mEL4%N1,mEL4%N2, X, Y, DetJ);
T0p=0;
DO i=1, mEL4%NBN
Ndx(i)=mEL4%N1(i,p)*J_inv(1,1) + mEL4%N2(i,p)*J_inv(1,2) ! [m-1]
Ndy(i)=mEL4%N1(i,p)*J_inv(2,1) + mEL4%N2(i,p)*J_inv(2,2) ! [m-1]
Ni = mEL4%Nf(i,p);
T0p = T0p + Temp_0(i)*Ni;
END DO;
detJ = abs(detJ)*mEL4%W(p); ! [m2]
DO N=1,mEL4%NBN
DO I=1,mEL4%NBN
Ni = mEL4%Nf(i,p);
Nn = mEL4%Nf(n,p);
Hin = mK*(Ndx(n)*Ndx(i) + Ndy(n)*Ndy(i))*DetJ; ! Wzór (4.14)
Cin = mC*mR*Nn*Ni*detJ; ! Wzór (5.3)
est(n,i) = est(n,i) + Hin + Cin/mdTime; ! Wzór (5.8)
r(n) = r(n) + (Cin/mdTime)*T0p;
END DO
! Q = 0.8*Tp*Hp
! r(n)=r(n) + Nn*Q*DetJ;
END DO
END DO
end subroutine PRE_heat_mat;
Rys. 9.10. Программа расчета компонентов матрицы жесткости и вектора нагрузок КЭ NEL.
1.3.7. Программа учета граничных условий
Программа учета граничных условий в матрице жесткости и векторе нагрузок показана на rys. 9.11. Для текущего КЭ выполняется цикл по всем контакнтым поверхностям (их число равно mGr%EL(NEL)%nPov). Затем выполняется интегрирование по каждой такой поверхности.
subroutine PRE_heat_pov_mat( NEL );
! ****************************************************
! WARUNKI BRZEGOWE
! Milenin Andre, AGH, 2008, milenin@agh.edu.pl
! ****************************************************
use GlobData;
implicit none;
integer*4 :: NEL;
INTEGER*4 :: I,j,N,P,Id,iPov;
REAL*8 :: DetJ,Ni,Nn,Pn;
REAL*8, DIMENSION(4) :: X,Y;
DO I=1,4
Id = ABS(mGr%EL(NEL)%NOP(I));
X(I) = mGr%nd(Id)%x /1000.0; ! [m]
Y(I) = mGr%nd(Id)%y /1000.0; ! [m]
END DO
DO iPov=1, mGr%EL(NEL)%nPov
id = mGr%EL(NEL)%aPov(iPov); ! Lokalny numer powierzchni elementu
SELECT CASE (id)
case(1)
DetJ=sqrt( (X(4)-X(1))**2 + (Y(4)-Y(1))**2 );
case(2)
DetJ=sqrt( (X(1)-X(2))**2 + (Y(1)-Y(2))**2 );
case(3)
DetJ=sqrt( (X(2)-X(3))**2 + (Y(2)-Y(3))**2 );
case(4)
DetJ=sqrt( (X(3)-X(4))**2 + (Y(3)-Y(4))**2 );
END SELECT
DO P=1, 2
DO n=1, 4
! Pętla po grupach równań równych wierszom macierzy
DO i=1, 4
! Pętla po kolumnach macierzy
Ni = mEL4%Sf(id)%Nf(i,p);
Nn = mEL4%Sf(id)%Nf(n,p);
est(n,i) = est(n,i) + mAlfa*Nn*Ni*DetJ; ! Wzór (4.14)
END DO
Pn = mAlfa*mT_otoczenia*Nn*DetJ; ! Wzór (4.15)
R(n) = R(n) + Pn;
END DO
END DO ! P
END DO; ! iPov
end subroutine PRE_heat_pov_mat;
Rys. 9.11. Программа учета граничных условий для текущего КЭ.
1.4. Пример расчета
Результаты расчета для данныйх, приведенных на rys. 9.1 показаны на rys. 9.12 для точки в центре сечения (кривая 1) и на его поверхности (кривая 2).
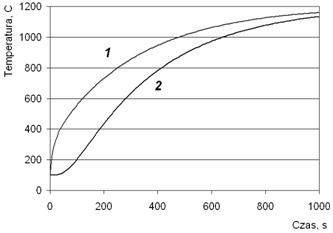
Rys. 9.12. Пример результатов расчета для точки в центре сечения (кривая 1) и на его поверхности (кривая 2).