Modelowanie naprężenia uplastyczniającego za pomocą modelu Makswela

1. Wstęp

Mechaniczny analog modelu Makswela przedstawiony na rys. 1.

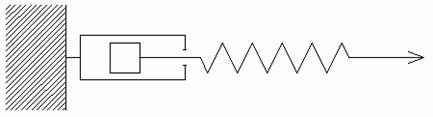
Rys. 1.

W modelu Makswela zakładamy, że sumaryczne odkształcenie składa

się z komponenty sprężystej i plastycznej, odpowiednie rys. 1:

(1)

Po różniczkowaniu równania (1) po czasie t, otrzymujemy równanie:

, (2)

gdzie E – moduł Younga, - współczynnik lepkości.

Oznaczymy:

, (3)

wtedy równanie (2) można zapisać w sposób następujący:

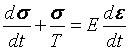(4)

Rozwiązanie równania (4) ma postać:

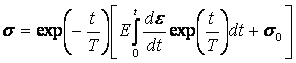. (5)

Dla warunku

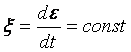(6)

rozwiązanie równania (5) ma postać:

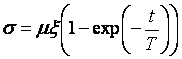, (7)

Natomiast dla pauzy podczas odkształcenia relaksacja naprężenia może być opisana formują:

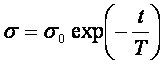(8)

2. Plan badan

a. Za pomocą metody różnic skończonych przedstawimy równanie (4) w postaci:

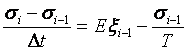. (9)

Za pomocą schematu jawnego wyznaczymy

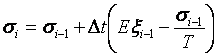(10)

b. Zadać historie odkształcenia w postaci (albo w postaci tabelowej).

Na początku odkształcenia

c. Napisać program do realizacji modelu (10).

3. Zadanie

a. Przeanalizować zależność naprężenia uplastyczniającego od historii odkształcenia;

– wpływ materiału (parametrów E i )

– wpływ pauzy w odkształceniu;

– wpływ zmian prędkości odkształcenia;

b. Pokazać, że przy tych samych końcowych parametrach odkształcenia

w zależności od historii odkształcenia wynik obliczenia naprężenia może być istotnie różny.