1.    PRZYKŁAD oprogramowania MES 

1.1.   Sformułowanie problemu

W ostatnim rozdziale niniejszego opracowania przedstawiono przykład oprogramowania, które stanowi rozwiązanie zagadnienia nieustalonej wymiany ciepła w układzie dwuwymiarowym. Podstawy teoretyczne tego rozwiązania są podane w rozdziałach 5 i 6. Układ równań MES uzyskano za pomocą wzoru (6.8):

,                                                                                    (6.8)

gdzie poszczególne wyrażenia obliczono za pomocą równań (5.14), (5.15) i (6.3):

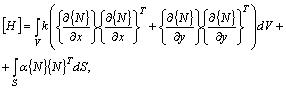                                                     (5.14)

,                                                                                                             (5.15)

.                                                                                                           (6.3)

We wzorze (6.8) {t1} oznacza wartości temperatur węzłowych po czasie , natomiast wektor {t0}  reprezentuje temperatury węzłowe w chwili .

Ponieważ analogiczną postać mają równania dla zadań dyfuzji, dlatego opracowany program po zmianie współczynników można wykorzystać do modelowaniu procesów dyfuzji. Wyzerowanie macierzy [C] spowoduje rozwiązanie ustalonego zadania cieplnego albo innego zadania opartego na równaniu Poissona (3.65).

1.2.   Dane wejściowe

Dane wejściowe do opracowanego programu są zadawane w postaci pliku tekstowego. Przykładową zawartość takiego pliku wraz z opisem wczytywanych zmiennych pokazano na rys. 9.1.

 

100     mTbegin                   Temperatura początkowa, C

1000    mTime                     Czas procesu, s

1       mdTime                                     Krok czasowy, s

1200    mT_otoczenia         Temperatura otoczenia C

300     mAlfa                                       Współczynnik wymiany ciepła  W/Cm2

100     mH0                                        Wysokość przekroju, mm

100     mB0                                        Szerokość przekroju, mm

25      mNhH                                       Liczba węzłów po wysokości

25      mNhH                                       Liczba węzłów po szerokości

700     mC                           Ciepło właściwe, J/Ckg

25      mK                             Współczynnik przewodzenia ciepła

7800    mR                                         Gęstość kg/m3

Rys. 9.1. Przykład zawartości pliku z danymi do obliczeń

1.3.   Kod źródłowy programu 

Program zawiera kilku modułów, a zawartość najważniejszych z nich jest opisana poniżej. Pełny tekst programu napisanego w języku FORTRAN90 można znaleźć na stronie internetowej http://home.agh.edu.pl/~milenin/programs/. 

1.3.1.    Program główny TEMP2D

Kod źródłowy programu głównego TEMP2D jest podany na rys. 9.2. Oznaczenia głównych zmiennych są następujące:

GlobData – nazwa modułu z opisem globalnych zmiennych;

dTauMax – maksymalnie dopuszczalny krok czasowy, który obliczono z warunku numerycznej stabilności rozwiązania;

n, Ntau – odpowiednio numer bieżącego kroku czasowego i ilość kroków czasowych;

Oznaczenia głównych procedur, które są wywoływane w programie głównym to:

IniEL4 – procedura inicjalizacji danych dla wybranego typu elementu skończonego (wybrany typ: 4-węzłowy element, opisany w rozdziale (4.9));

InpData – wczytywanie danych wejściowych;

GenGrid2d – rozbudowa siatki MES dla obszaru o przekroju prostokątnym;

SetControlPoints – definicja punktów, z jakich będą wyprowadzane wyniki rozwiązania do pliku tekstowego;

ALLOCATE_Matrix – przydzielenie pamięci dla macierzy;

WriteControlPointsBegin – zapis do pliku wyników obliczeń, które wykonano na podstawie danych wstępnych;

WriteControlPoints – zapis wyników obliczeń do pliku;

SOLVER – procedura rozwiązywania zadania dla bieżącego kroku czasowego.

program TEMP2D

!*************************************************************************

!  PROGRAM: TEMP2D

!  Milenin Andre, AGH, 2008, milenin@agh.edu.pl

!************************************************************************

               use GlobData;

               implicit none

               real*8    :: Asr,dTauMax,TauP;

               integer*4 :: n, Ntau, i, iErr;

call IniEL4();                                                                    

call InpData();                                                                 

call GenGrid2d(mH0,mB0,mNhH,mNhB, mGr);            

call SetControlPoints();                                                  

CALL ALLOCATE_Matrix();                                            

CALL WriteControlPointsBegin();

               Asr  = mK / (mC * mR);

               mdTime = DBLE(mB0/(1e3*mNhB))**2/(0.5*Asr);

CALL WriteControlPoints();

               Ntau = int(mTime/mdTime)+1;

               mdTime = mTime/DBLE(Ntau);

               mTau    = 0;

               do n=1, Ntau

                              mTau = mTau + mdTime;

                              CALL SOLVER(  );

                              CALL WriteControlPoints();

               end do;

               CLOSE(88);         CLOSE(89);

               DEALLOCATE ( mA, STAT=iErr );

               DEALLOCATE ( mB, STAT=iErr );

               DEALLOCATE ( mX, STAT=iErr );

end program TEMP2D

Rys. 9.2. Program główny TEMP2D

1.3.2.    Modułi z definicją struktur danych i zmiennych  globalnych

Wykorzystanie struktur danych ułatwia proces programowania i analizy kodu. Na rys. 9.3 pokazano kod źródłowy modułu My_typ z definicją struktur danych. Wykorzystano w nim następujące struktury:

Node – struktura danych, zawierająca informacje o węźle siatki: x, y – współrzędne węzła, t – temperatura w węźle, CR – prędkość zmiany temperatury;

Element – struktura danych, zawierająca informacje o elemencie siatki MES: nop – mapa elementu (rozdział 7.2.1), Npov – liczba powierzchni elementu, które kontaktują się z otoczeniem; aPov – lokalne numery powierzchni stykowych elementu.

gr2d – struktura danych, zawierająca siatkę MES: nh – liczba węzłów; ne – liczba elementów; nbn – liczba węzłów w wykorzystywanym elemencie skończonym; ncn – liczba zmiennych w elemencie skończonym, która dla zadań cieplnych odpowiada nbn; nhPov – liczba węzłów siatki znajdujących się na powierzchni rozpatrywanego obszaru; EL –macierz o długości ne zawierająca dane typu Element dla każdego elementu siatki; ND –macierz o długości nh zawierająca dane typu Node dla każdego węzła siatki.

cor_L – struktura danych, która zawiera współrzędne N, E punktu w układzie lokalnym dla elementu.

Gran – struktura danych, zawierająca dane o krawędziach powierzchniowych wykorzystywanego elementu skończonego: N_p – liczba punktów całkowania po powierzchni krawędzi; P – macierz elementów typu cor_L o długości N_p zawierająca współrzędne lokalne punktów całkowania Gaussa; W – macierz o długości N_p zawierająca wagi punktów całkowania odpowiednio uwzględnione we wzorze (4.31); Nf – macierz o wymiarach nbn zawierająca wartości funkcji kształtu elementu, które są obliczone w punktach całkowania na powierzchni krawędzi; N1,N2 – macierze o wymiarach nbn zawierające wartości pochodnych funkcji kształtu względem współrzędnych lokalnych, które są obliczone w punktach całkowania na powierzchni krawędzi; UZEL – macierz zawierająca lokalne numery węzłów krawędzi.

ELEM – struktura danych, zawierająca dane o wykorzystywanym elemencie skończonym: nbn – liczba węzłów w analizowanym elemencie skończonym, nbnp – liczba węzłów w analizowanym elemencie skończonym do interpolacji średniego naprężenia (wykorzystywana w zadaniach teorii plastyczności), N_p – liczba punktów całkowania w objętości elementu; Nf – macierz o wymiarach nbn zawierająca wartości funkcji kształtu elementu, które są obliczane w punktach całkowania w objętości elementu; N1, N2 – macierze o wymiarach nbn zawierające wartości pochodnych funkcji kształtu względem współrzędnych lokalnych, które są obliczane w punktach całkowania w objętości wykorzystywanego elementu skończonego; P – macierz elementów typu cor_L o długości N_p zawierająca współrzędne lokalne punktów całkowania Gaussa w objętości elementu; L –macierz elementów typu cor_L o długości N_p zawierająca współrzędne lokalne węzłów elementu; W – macierz o długości N_p zawierająca wagi punktów całkowania w objętości elementu odpowiednio we wzorze (4.31); Sf – macierz o długości równej maksymalnej liczbie powierzchni wykorzystanego elementu skończonego (tutaj równa 4), która zawiera elementy typu Gran.

 

module My_typ;

! ******************************************************************

! Typy danych

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

implicit none;

               type node

                              real*8 :: x,y,t,CR;

                              integer*4 :: status;

               end type

               type element

               integer*4 :: nop(4);

               integer*4 :: Npov;                 ! Liczba kontaktowych powierzchni elementu 0-1-2

               integer*4 :: aPov(2);            !  Lokalne numery kontaktowych powierzchni elementu

               end type

               type gr2d

                              integer*4 :: nh, ne, nbn, ncn, nhPov;

                              type(element) , dimension(:), pointer :: EL;

                              type(node) , dimension(:), pointer :: ND;

               end type

               type cor_L;

real*8 N, E;

               end type cor_L;

               type Gran

                               integer*4 :: N_p;   ! Liczba punktów całkowania po powierzchni grani

                               type(cor_L), dimension(:), pointer :: P;

                                real*8, dimension(:), pointer      ::    W;

                                real*8, dimension(:,:), pointer    :: N1,N2,Nf;   ! N1(nbn,N_p)

                                integer*1, dimension(:),pointer        :: UZEL;

                              ! Lokalne numery węzłów grani

               end type Gran;

type ELEM;

       integer*4 :: nbn, nbnp, N_p;

       real*8, dimension(:,:), pointer :: N1,N2,Nf;        ! N1(nbn,N_p)

       type(cor_L), dimension(:), pointer :: P;             ! P(N_p)

       type(cor_L), dimension(:), pointer :: L; ! Współrzędne węzłów elementu

       real*8, dimension(:), pointer :: W;      ! Waga punktów całkowania W(N_p)

       type(Gran) :: Sf(4);

               end type ELEM;

end module My_typ;

Rys. 9.3. Typy (struktury) danych potrzebne do otrzymania rozwiązania

Moduł GlobData zawiera definicje zmiennych, które są używane we wszystkich procedurach, gdzie zadeklarowano wykorzystanie tego modułu: use GlobData. Dokładny opis zmiennych podano na rys. 9.4.

 

module GlobData;

! ******************************************************************

! Globalne zmianne

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

use My_typ;

implicit none;

               real*8       ::  mTbegin;                        ! Początkowa temperatura

               real*8       ::  mTime;                          ! Czas procesu

               real*8       ::  mdTime;                        ! Początkowa wartość przyrostu czasu

               real*8       ::  mTau;                            ! Bieżący czas

               real*8       ::  mT_otoczenia;              ! Temperatura otoczenia

               real*8       ::  mAlfa;                            ! Współczynnik wymiany ciepła

               real*8       ::  mH0;                              ! Wysokość przekroju

               real*8       ::  mB0;                              ! Szerokość przekroju

               integer*4    ::  mNhH;                         ! Liczba węzłów na wysokości przekroju

               integer*4    ::  mNhB;                         ! Liczba węzłów na szerokości przekroju

               integer*4    ::  mLDA;                         ! Szerokość pasma matrycy MES

               real*8       ::  mC;                                ! Pojemność cieplna

               real*8       ::  mK;                                ! Współczynnik przewodzenia ciepła

               real*8       ::  mR;                                ! Gęstość

               type(gr2d)   :: mGr;                            ! Siatka MES

               type(ELEM)   :: mEL4;                       ! Dane uszytego elementu skończonego

               integer*4 :: mContrPoints(9);             ! Kontrolne punkty

               REAL*8    :: mcpX(9),mcpY(9);

               real*8, dimension(4,4) :: est;             ! Matryca bieżącego elementu

               real*8, dimension(4)   :: r;                  ! Wektor obciążeń bieżącego elementu

               real*8, dimension(:),   allocatable :: mB; ! Globalny wektor obciążeń

               real*8, dimension(:,:), allocatable :: mA; ! Globalna matryca

               real*8, dimension(:),   allocatable :: mX; ! Globalny wektor niewiadomych

end module GlobData;

Rys. 9.4. Zmienne globalne wykorzystywane w programie

1.3.3.    Procedura inicjalizacji danych dla elementu 

Wypełnienie zmiennej mEL4 typu ELEM odbywa się w programie IniEL4 pokazanym na rys. 9.5. W pierwszej części programu zadano liczbę węzłów elementu nbn równą 4. Wybrany schemat całkowania numerycznego zawiera 4 punkty, tak jak na rys. 4.19, dlatego zadano N_p=4. Przydzielono pamięć macierzom N1, N2, Nf, P, W oraz L. Następnie wypełniono współrzędne lokalne punktów całkowania zgodnie z rys. 4.19. Obliczono w każdym punkcie całkowania wartości N1, N2 i Nf wykorzystując wzory (4.9).

Analogicznie wypełniono struktury dla 4 powierzchni wybranego elementu.

Przy wykorzystaniu innego typu elementów skończonych jest wymagana zmiana struktury mEL4 i siatki elementów.

 

SUBROUTINE IniEL4();

! ******************************************************************

! Inicjalizacja danych dla elementu

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

use GlobData;

implicit none;

REAL*8    :: Alfa,L1,L2,e,n,SN;

integer*4 :: iP,i;

 

               Alfa = 1/(sqrt(4.0));

               mEL4%nbn=4;

               mEL4%N_p=4;

               ALLOCATE(mEL4%N1( mEL4%nbn, mEL4%N_p ));

               ALLOCATE(mEL4%N2( mEL4%nbn, mEL4%N_p ));

               ALLOCATE(mEL4%Nf( mEL4%nbn, mEL4%N_p ));

               ALLOCATE(mEL4%P ( mEL4%N_p ));

               ALLOCATE(mEL4%W ( mEL4%N_p ));

               ALLOCATE(mEL4%L ( mEL4%nbn ));

               mEL4%W = 1.0;

               mEL4%P(1)%E = -Alfa;

               mEL4%P(1)%N = -Alfa;

               mEL4%P(2)%E =  Alfa;

               mEL4%P(2)%N = -Alfa;

               mEL4%P(3)%E =  Alfa;

               mEL4%P(3)%N =  Alfa;

               mEL4%P(4)%E = -Alfa;

               mEL4%P(4)%N =  Alfa;

               mEL4%L(1)%E = -1;

               mEL4%L(1)%N = -1;

               mEL4%L(2)%E =  1;

               mEL4%L(2)%N = -1;

               mEL4%L(3)%E =  1;

               mEL4%L(3)%N =  1;

               mEL4%L(4)%E = -1;

               mEL4%L(4)%N =  1;

               DO iP = 1, mEL4%N_p

                              L1 = mEL4%P(iP)%E

                              L2 = mEL4%P(iP)%N

                              mEL4%Nf(1,iP) =  0.25*(1-L1)*(1-L2);

                              mEL4%N1(1,iP) = -0.25*(1-L2);

                              mEL4%N2(1,iP) = -0.25*(1-L1);

                              mEL4%Nf(2,iP) =  0.25*(1+L1)*(1-L2);

                              mEL4%N1(2,iP) =  0.25*(1-L2);

                              mEL4%N2(2,iP) = -0.25*(1+L1);

                              mEL4%Nf(3,iP) =  0.25*(1+L1)*(1+L2);

                              mEL4%N1(3,iP) =  0.25*(1+L2);

                              mEL4%N2(3,iP) =  0.25*(1+L1);

                              mEL4%Nf(4,iP) =  0.25*(1-L1)*(1+L2);

                              mEL4%N1(4,iP) = -0.25*(1+L2);

                              mEL4%N2(4,iP) =  0.25*(1-L1);

               end do;

               DO i = 1, 4

                              mEL4%Sf(i)%N_p = 2;

                              ALLOCATE( mEL4%Sf(i)%P( mEL4%Sf(i)%N_p ) );

                              ALLOCATE( mEL4%Sf(i)%W( mEL4%Sf(i)%N_p ) );

                              mEL4%Sf(i)%W = 1;

                              ALLOCATE( mEL4%Sf(i)%N1( mEL4%nbn, mEL4%Sf(i)%N_p));

                              ALLOCATE( mEL4%Sf(i)%N2( mEL4%nbn, mEL4%Sf(i)%N_p));

                              ALLOCATE( mEL4%Sf(i)%Nf( mEL4%nbn, mEL4%Sf(i)%N_p));

                              ALLOCATE( mEL4%Sf(i)%UZEL( 2 ) );

               END DO;

               mEL4%Sf(1)%UZEL(1) = 4;              mEL4%Sf(1)%UZEL(2) = 1;

               mEL4%Sf(2)%UZEL(1) = 1;              mEL4%Sf(2)%UZEL(2) = 2;

               mEL4%Sf(3)%UZEL(1) = 2;              mEL4%Sf(3)%UZEL(2) = 3;

               mEL4%Sf(4)%UZEL(1) = 3;              mEL4%Sf(4)%UZEL(2) = 4;

               mEL4%Sf(1)%P(1)%N=Alfa;             mEL4%Sf(1)%P(1)%E=-1;

               mEL4%Sf(1)%P(2)%N=-Alfa;            mEL4%Sf(1)%P(2)%E=-1;

               mEL4%Sf(2)%P(1)%N=-1;                mEL4%Sf(2)%P(1)%E=-Alfa;

               mEL4%Sf(2)%P(2)%N=-1;                mEL4%Sf(2)%P(2)%E=Alfa;

               mEL4%Sf(3)%P(1)%N=-Alfa;            mEL4%Sf(3)%P(1)%E=1;

               mEL4%Sf(3)%P(2)%N=Alfa;             mEL4%Sf(3)%P(2)%E=1;

               mEL4%Sf(4)%P(1)%N=1;                 mEL4%Sf(4)%P(1)%E=Alfa;

               mEL4%Sf(4)%P(2)%N=1;                 mEL4%Sf(4)%P(2)%E=-Alfa;

               do i = 1, 4

                              DO iP = 1, 2

                                            e = mEL4%Sf(i)%P(ip)%E;

                                            n = mEL4%Sf(i)%P(ip)%N;

                                            mEL4%Sf(i)%Nf(1,ip) = 0.25*(1-e)*(1-n);

                                            mEL4%Sf(i)%Nf(2,ip) = 0.25*(1+e)*(1-n);

                                            mEL4%Sf(i)%Nf(3,ip) = 0.25*(1+e)*(1+n);

                                            mEL4%Sf(i)%Nf(4,ip) = 0.25*(1-e)*(1+n);

                                            mEL4%Sf(i)%N1(1,ip) = -0.25*(1-n);

                                            mEL4%Sf(i)%N1(2,ip) = 0.25*(1-n);

                                            mEL4%Sf(i)%N1(3,ip) = 0.25*(1+n);

                                            mEL4%Sf(i)%N1(4,ip) = -0.25*(1+n);

                                            mEL4%Sf(i)%N2(1,ip) = -0.25*(1-e);

                                            mEL4%Sf(i)%N2(2,ip) = -0.25*(1+e);

                                            mEL4%Sf(i)%N2(3,ip) = 0.25*(1+e);

                                            mEL4%Sf(i)%N2(4,ip) = 0.25*(1-e);

                              END DO;

               end do;

END SUBROUTINE IniEL4;

Rys. 9.5. Inicjalizacja danych dla elementu skonczonego

1.3.4.    Procedury wczytywania danych i przydzielenia pamięci dla macierzy 

Program do wczytywania danych jest pokazany na rys. 9.6. Program ten otwiera plik tekstowy indata.t2d, którego struktura jest opisana w podrozdziale 9.2.

 

Subroutine InpData();

! ******************************************************************

! Wczytywanie danych

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

use GlobData;

implicit none;

integer nFile,i,j,iost;

 

               nFile = 89

               OPEN (nFile, FILE='indata.t2d', action='read')

               read(nFile, *);

               read(nFile, *);

               read(nFile, *);

               read(nFile, *);

               read(nFile, *) mTbegin;

               read(nFile, *) mTime;

               read(nFile, *) mdTime;

               read(nFile, *) mT_otoczenia;

               read(nFile, *) mAlfa;

               read(nFile, *) mH0;

               read(nFile, *) mB0;

               read(nFile, *) mNhH;

               read(nFile, *) mNhB;

               read(nFile, *) mC;

               read(nFile, *) mK;

               read(nFile, *) mR;

               close (nFile);

end Subroutine InpData

Rys. 9.6. Program do wczytywania danych.

Przydzielenie pamięci dla macierzy odbywa się poprzez obliczenie szerokości mLDA macierzy sztywności za pomocą mapy elementów oraz przydzielenie pamięci zmiennym mA (globalna macierz sztywności), mX (wektor niewiadomych) i mB (wektor obciążeń). W celach metodycznych pokazano, jak przydzielić pamięć dla pełnej matrycy o wymiarach nh*nh. Ten wariant prowadzi do nieskutecznego wykorzystania pamięci, ale jest prostszy do zrozumienia.

 

SUBROUTINE ALLOCATE_Matrix;

use GlobData;

implicit none;

integer*4 :: NEL, i, j, ii, jj, jB, nk(4),NeMaxB, ierr;

 

               mLDA=0;

               do NEL = 1,mGr%ne

                              do i=1,mEL4%nbn

                                            nk(i) = mGr%EL(NEL)%nop(i);

                              end do;

                              do i=1,mEL4%nbn

! * ii - wiersz *

                                            ii=nk(i);

                                            do j=1,mEL4%nbn

                                            ! * jj - kolumna *

                                                           jj=nk(j);

                                                           jB = jj-ii+1;

                                                           if(jB>=mLDA) then

                                                           mLDA=jB;

                                                           NeMaxB = NEL;

                                                           end if;

                                            end do;

                              end do;

               end do;

 

               ALLOCATE ( mA(mLDA, mGr%nh), STAT=iErr );

!              ALLOCATE ( mA(mGr%nh, mGr%nh), STAT=iErr );

!              Pelna matryca MES

               ALLOCATE ( mB(mGr%nh), STAT=iErr );

               ALLOCATE ( mX(mGr%nh), STAT=iErr );

END SUBROUTINE ALLOCATE_Matrix

Rys. 9.7. Program do obliczenia pamięci potrzebnej dla globalnej macierzy sztywności.

1.3.5.    Procedura rozwiązywania zadania dla bieżącego kroku czasowego

Program do rozwiązywania zadania dla bieżącego kroku czasowego jest pokazany na rys. 9.8.

 

SUBROUTINE SOLVER( );

! ******************************************************************

!             Solver

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

use GlobData;

use msimsl;

implicit none;

integer*4  :: NEL;

integer*4, dimension(4)   :: nk;

integer*4 :: jB,iB,NeMaxB,NCODA,i,j,ii,jj;

integer*4 :: iErr;

               mA=0;    mB=0;    mX=0;

               do NEL=1, mGr%ne

                              do i=1, mEL4%nbn

                                            nk(i) = mGr%EL(NEL)%nop(i);

                              end do;

                              CALL FeSM_heat( NEL );

                              do i=1, mEL4%nbn

                                            ii = nk(i);                               ! wiersz w macierzy pełnej

                                            do j=1, mEL4%nbn

                                                           jj = nk(j);                ! Kolumna w macierzy pełnej

                                                           iB = mLDA + ii - jj;! Wiersz w macierzy pasmowej

                                                           if ((jj>=ii).AND.(iB<=mLDA)) then

                              mA(iB, jj) = mA(iB, jj) + est(i,j);          ! Wypełnienie macierzy pasmowej

                                                           end if;           

               !              mA(ii,jj) = mA(ii,jj) + est(i,j);                ! Wypełnienie macierzy pełnej

                                            end do;

                                            mB(ii) = mB(ii) + r(i);

                              end do;

               end do;

               NCODA = mLDA-1;

               CALL DLSAQS (mGr%nh, mA, mLDA, NCODA, mB, mX)

! Program do rozwiązania układu równań z macierzą pasmową

!              NCODA=1;

!              CALL DLSARG (mGr%nh, mA, mGr%nh, mB, NCODA, mX)

! Program do rozwiązania układu równań z macierzą pełną

               do i=1, mGr%nh

                              mGr%nd(i)%CR = ( mGr%nd(i)%t-mX(i) ) / mdTime;

                              mGr%nd(i)%t = mX(i);

               end do;

END SUBROUTINE SOLVER;

Rys. 9.8. Program do wypełnienia macierzy globalnej i rozwiązania układu równań MES

W tym programie oznaczenia zmiennych są następujące:

NEL – bieżący numer elementu;

Nk – macierz zawierającą mapę bieżącego elementu;

FeSM_heat – program wypełnienia macierzy i wektora obciążeń bieżącego elementu NEL;

DLSAQS – program rozwiązania układu równań z macierzą pasmową;

DLSARG – program rozwiązania układu równań z pełną matrycą (podano jako komentarz w celach metodycznych).

1.3.6.    Procedura wypełnienia macierzy sztywności i wektora obciążeń

Program FeSM_heat (rys. 9.9) zawiera dwie części:

PRE_heat_mat –  wypełnia macierz i wektor obciążeń;

PRE_heat_pov_mat – uwzględnia warunki brzegowe.

 

SUBROUTINE FeSM_heat( NEL );

! ******************************************************************

! Generacja macierzy elementu NEL

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ******************************************************************

use GlobData;

implicit none;

integer*4  :: NEL;  ! Numer bieżącego Elementu

               est = 0;  

               r = 0;

               call PRE_heat_mat( NEL );

               call PRE_heat_pov_mat(NEL );

END SUBROUTINE FeSM_heat;

Rys. 9.9. Program do obliczenia macierzy sztywności bieżącego elementu (NEL)

Program PRE_heat_mat pokazano na rys. 9.10. Program Jacob_2d zostaje wywołany, co zostało opisane w rozdziale 4.6 i podane w uproszczonej postaci na rys. 4.26. Program ten realizuje typowy algorytm wypełnienia macierzy jednego elementu, który został wielokrotnie opisany w niniejszym opracowaniu. W tekście programu są podane odwołania do wzorów, które są wykorzystywane podczas obliczania składowych macierzy.  

 

subroutine PRE_heat_mat( NEL );

use GlobData;

implicit none;

integer*4  :: NEL; 

INTEGER*4  :: I,j,N,P,Id;

REAL*8, DIMENSION(2,2) :: J_,J_inv; ! Macierz Jakobiego i macierz odwrotna

REAL*8     :: DetJ,Ni,Nn,Hin,Cin;

real*8        :: T0p;

REAL*8, DIMENSION(4)   :: Ndx,Ndy;  ! Pochodne funkcji kształtu względem X i Y

REAL*8, DIMENSION(4)   :: X,Y,Temp_0; 

               DO I=1,mEL4%NBN

                              Id = ABS( mGr%EL(NEL)%NOP(I) );

                              X(I)  = mGr%nd(Id)%x /1000.0;         ! [m]

                              Y(I)  = mGr%nd(Id)%y /1000.0;         ! [m]

                              Temp_0(i)= mGr%nd(Id)%t;                                  

               END DO

               DO P=1, mEL4%N_p

CALL Jacob_2d(J_, J_inv, P, mEL4%N_p, mEL4%NBN, mEL4%N1,mEL4%N2, X, Y, DetJ);

                              T0p=0;

                              DO i=1, mEL4%NBN

                              Ndx(i)=mEL4%N1(i,p)*J_inv(1,1) + mEL4%N2(i,p)*J_inv(1,2) ! [m-1]

                              Ndy(i)=mEL4%N1(i,p)*J_inv(2,1) + mEL4%N2(i,p)*J_inv(2,2) ! [m-1]

                              Ni = mEL4%Nf(i,p);

                              T0p = T0p + Temp_0(i)*Ni;

                              END DO;

                              detJ = abs(detJ)*mEL4%W(p);  ! [m2]

                   DO N=1,mEL4%NBN

                                             DO I=1,mEL4%NBN  

                                              Ni = mEL4%Nf(i,p);

                                              Nn = mEL4%Nf(n,p);

                                Hin = mK*(Ndx(n)*Ndx(i) + Ndy(n)*Ndy(i))*DetJ;          ! Wzór (4.14)

                                Cin = mC*mR*Nn*Ni*detJ;                                           ! Wzór (5.3)

est(n,i) = est(n,i) + Hin + Cin/mdTime;                     ! Wzór (5.8)

                                            r(n)  = r(n) + (Cin/mdTime)*T0p;

                                  END DO

!                                           Q = 0.8*Tp*Hp

!                                           r(n)=r(n) + Nn*Q*DetJ;

                               END DO

               END DO

end subroutine PRE_heat_mat;

Rys. 9.10. Program do obliczenia składowych macierzy sztywności bieżącego elementu NEL.

1.3.7.    Procedura z warunkami brzegowymi

Program uwzględniający warunki brzegowe w macierzy sztywności elementu pokazano na rys. 9.11. W programie dla bieżącego elementu jest realizowana pętla po powierzchniach styku tego elementu z otoczeniem (ich liczba jest równa mGr%EL(NEL)%nPov). Następnie zachodzi całkowanie po każdej powierzchni za pomocą wybranego w programie IniEL4 schematu całkowania. W tekście programu podane są odwołania do wzorów wykorzystywanych podczas obliczania poprawek do składowych macierzy i wektora obciążeń.

 

subroutine PRE_heat_pov_mat( NEL );

! ****************************************************

! WARUNKI BRZEGOWE

! Milenin Andre, AGH, 2008, milenin@agh.edu.pl

! ****************************************************

use GlobData;

implicit none;

integer*4                              :: NEL;   

INTEGER*4                         :: I,j,N,P,Id,iPov;

REAL*8                               :: DetJ,Ni,Nn,Pn;

REAL*8, DIMENSION(4)     :: X,Y; 

               DO I=1,4

                              Id = ABS(mGr%EL(NEL)%NOP(I));

                              X(I)  = mGr%nd(Id)%x /1000.0;         ! [m]

                              Y(I)  = mGr%nd(Id)%y /1000.0;         ! [m]

               END DO

               DO iPov=1, mGr%EL(NEL)%nPov

               id = mGr%EL(NEL)%aPov(iPov); ! Lokalny numer powierzchni elementu

                              SELECT CASE (id)

                              case(1)                               

                              DetJ=sqrt( (X(4)-X(1))**2 + (Y(4)-Y(1))**2 );

                              case(2)                               

                              DetJ=sqrt( (X(1)-X(2))**2 + (Y(1)-Y(2))**2 );

                              case(3)                               

                              DetJ=sqrt( (X(2)-X(3))**2 + (Y(2)-Y(3))**2 );

                              case(4)                               

                              DetJ=sqrt( (X(3)-X(4))**2 + (Y(3)-Y(4))**2 );

                              END SELECT

                              DO P=1, 2

                                            DO n=1, 4

                                ! Pętla po grupach równań równych wierszom macierzy

                                                           DO i=1, 4

                                              ! Pętla po kolumnach macierzy

                                                           Ni = mEL4%Sf(id)%Nf(i,p);

                                                           Nn = mEL4%Sf(id)%Nf(n,p);

                                            est(n,i) = est(n,i) + mAlfa*Nn*Ni*DetJ;             ! Wzór (4.14)

                                                           END DO

                                            Pn = mAlfa*mT_otoczenia*Nn*DetJ;               ! Wzór (4.15)

                                                           R(n) = R(n) + Pn;

                                            END DO

                              END DO ! P

               END DO; ! iPov

end subroutine PRE_heat_pov_mat;

Rys. 9.11. Program uwzględniający warunki brzegowe w macierzy sztywności elementu.

1.4.  Przykład obliczeń

Wyniki obliczeń dla danych, które zamieszczono na rys. 9.1 są podane na rys. 9.12 dla punktu zlokalizowanego w środku przekroju (krzywa 1) i na jego powierzchni (krzywa 2).

Rys. 9.12. Przykład wyników obliczeń dla punktu zlokalizowanego w środku przekroju (krzywa 1) i na jego powierzchni (krzywa 2).

1.5.  Pytania kontrolne

1. Uruchomić opisaną wersje programu na podstawie projektu, który należy pobrać z Internetu. Następnie wykonać testowe obliczenia. Przykładowy wynik testowy jest pokazany na rys. 9.12. 

2. Napisać program z inicjalizacją danych dla elementu typu simpleks.

3. Napisać program z inicjalizacją danych dla elementu drugiego rzędu, który pokazano na rys. 4.12 przy wykorzystaniu schematu całkowania, jaki pokazano na rys. 4.20.

4. Napisać swój program do generacji siatki elementów drugiego rzędu (rys. 4.12) dla zadania 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.6.  Funkcje kształtu elementów wyższego rzędu

Rozpatrzmy kilka elementów wyższego rzędu. W praktyce rzadko stosowane są  elementy rzędu wyższego niż drugi, dlatego w dalszej analizie będą rozpatrywane izoparametryczne elementy drugiego rzędu.

Jednym z popularnych elementów jest element typu serendypowego (ang. serendipity family elements), rys. 4.11.

a)                                                                    b)

Rys. 4.11. Numeracja węzłów dwuwymiarowego 8- węzłowego elementu skończonego w układzie globalnym (a) i lokalnym (b).

a)                                                              b)

Rys. 4.12. Numeracja węzłów dwuwymiarowego 9- węzłowego elementu skończonego w układzie globalnym (a) i lokalnym (b).

Funkcje kształtu tego elementu w układzie lokalnym są zapisane w następujący sposób:

                                                                                                           (4.21)

.

 

Klasyczny element drugiego rzędu typu Lagrange'a zawiera 9 węzłów (rys. 4.12). Funkcje kształtu tego elementu w układzie lokalnym mają następującą postać:

 

                                                                                                     (4.22)

 

 

 

 

 

 

 

 

 

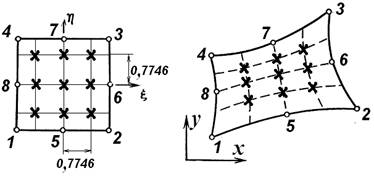
Schemat całkowania

 

 

 

 

            a)                                            b)

Rys. 4.20. Współrzędne punktów całkowania Gaussa dla całkowania numerycznego elementu drugiego rzędu w układzie a) lokalnym, b) globalnym