Omawiać
będziemy niektóre z
poleceń MATLAB-a oraz TOOLBOX-u Control System Toolbox, znajdujących
zastosowanie
w teorii liniowych układów regulacji automatycznej.
Matematyczny
opis liniowych
stacjonarnych układów sterowania przedstawia się zwykle w postaci
transmitancji
operatorowej (ang. transfer function) lub we współrzędnych stanu (ang.
state
space). Opis za pomocą transmitancji stosuje się najczęściej w
klasycznych,
jednowymiarowych układach regulacji automatycznej typu SISO (ang. Single
Input Single Output) oraz wielowyjściowych typu SIMO (Single Input
Multiple
Output). W układach
wielowymiarowych
typu MIMO (Multiple Input Multiple Output), przyjmuje się ogólniejszy i
bardziej dogodny opis w przestrzeni stanów. W tabeli 1 podano zestaw
poleceń
Toolbox-u Control System do konwersji każdego z tych opisów na
pozostałe.
Tabela 1. Polecenia
konwersji opisu układów
|
Nazwa |
Opis polecenia |
|
tf2ss |
transmitancja
operatorowa na równania stanu |
|
tf2zp |
transmitancja
operatorowa do postaci czynnikowej |
|
zp2ss |
postać czynnikowa
transmitancji na równania stanu |
|
zp2tf |
postać czynnikowa na
transmitancję operatorową |
|
ss2tf |
równania stanu na
transmitancję operatorową |
|
ss2zp |
równania stanu na
postać czynnikową transmitancji |
Układ liniowy
jednowymiarowy
można opisać za pomocą transmitancji operatorowej (tf) w postaci
ilorazu
wielomianów:
![]() (1)
(1)
gdzie L(s) jest wielomianem m-tego stopnia, M(s) jest wielomianem n-
tego
stopnia, przy czym zachodzi m « n.
We
współrzędnych stanu opis
układu ma postać:
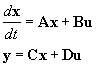 (2)
(2)
gdzie x(t)
jest n×1 wymiarowym
wektorem stanu układu, u(t) jest r×1 wymiarowym
wektorem wejścia (sterowania), y(t) jest m×1 wymiarowym
wektorem wyjścia, A jest n×n wymiarową
macierzą stanu, B jest n×r wymiarową
macierzą wejścia, C jest m×n wymiarową
macierzą wyjścia oraz D jest m×r wymiarową
macierzą przejścia (transmisji).
Tabela 2. Polecenia
konwersji opisu układu ciągłego na dyskretny i odwrotnie
|
Nazwa |
Opis polecenia |
|
c2d |
opis ciągły na dyskretny |
|
c2dt |
transmitancja operatorowa do
postaci czynnikowej |
|
c2dm |
postać czynnikowa transmitancji
na równania stanu |
|
d2c |
postać czynnikowa na
transmitancję operatorową |
|
d2cm |
równania stanu na transmitancję
operatorową |
Tabela 3. Polecenia
do wykonywania charakterystyk czasowych
|
Nazwa |
Opis polecenia |
|
step |
odpowiedź jednostkowa układu
ciągłego |
|
impulse |
odpowiedź impulsowa układu
ciągłego |
|
lsim |
symulacja układu ciągłego dla
danych wejść |
|
initial |
odpowiedź układu ciągłego przy
zadanych warunkach początkowych |
|
dstep |
odpowiedź jednostkowa układu
dyskretnego |
|
dimpulse |
odpowiedź impulsowa układu
dyskretnego |
|
dlsim |
symulacja układu dyskretnego dla
danych wejść |
|
dinitial |
odpowiedź układu dyskretnego
przy zadanych warunkach początkowych |
Polecenia
służące do
tworzenia charakterystyk czasowych: step, impulse, lsim,
initial
step
Polecenie step
wyznacza odpowiedź jednostkową układu dla danej transmitancji
operatorowej lub zadanego
opisu układu we współrzędnych stanu.
Składnia dla
zadanej
transmitancji operatorowej ma jedną z podanych postaci:
step(l,m)
step(l,m,t)
[y,x]=step(l,m,t)
[y,x,t]=step(l,m)
gdzie l = [bm
bm-1 ... b1 b0]
jest to wektor współczynników wielomianu licznika transmitancji,
m = [an an-1 ...
a1 a0] jest wektorem współczynników wielomianu
mianownika
tej transmitancji,
t jest zadanym wektorem czasu.
Wprowadzenie polecenia bez
argumentów lewostronnych,
spowoduje wykonanie wykresu odpowiedzi skokowej układu w zakresie
zdeterminowanym wektorem czasu t. Jeżeli czas nie został
wyspecyfikowany jako
argument prawostronny, to program przyjmuje automatycznie wektor czasu
i
również rysuje wykres. Wartości obliczonych wektorów nie są wypisywane
na
ekran. Podanie argumentów lewostronnych wstrzymuje wykonywanie wykresu,
natomiast mogą być wypisane ich wartości.
W przypadku
gdy znany jest
opis układu w przestrzeni stanu, stosowanie polecenia step ma
jedną z
możliwych postaci:
step(A,B,C,D,IU)
step(A,B,C,D,IU,t)
[y,x]=step(A,B,C,D,IU,t)
[y,x,t]=step(A,B,C,D,IU)
gdzie IU
jest
numerem wejścia, do którego przyłożono skok jednostkowy.
3.
Przykłady
analizy układów
dynamicznych
Przykład 1
Wyznaczyć
odpowiedź
jednostkową układu jednowymiarowego opisanego transmitancją operatorową
![]()
gdzie ![]() .
.
W oknie
poleceń MATLAB-a
(MATLAB Command Window) wprowadzamy sekwencję poleceń
>>l=3;m=[5 1];step(l,m)
Otrzymujemy w
wyniku wykres
odpowiedzi jednostkowej przedstawiony na rys. 1, w zakresie czasu
dobranym
automatycznie przez program, linią przerywaną zaznaczona jest wartość
ustalona
odpowiedzi. Skalowanie i opis układu współrzędnych ( w języku ang.)
odbywa się
również automatycznie[1].
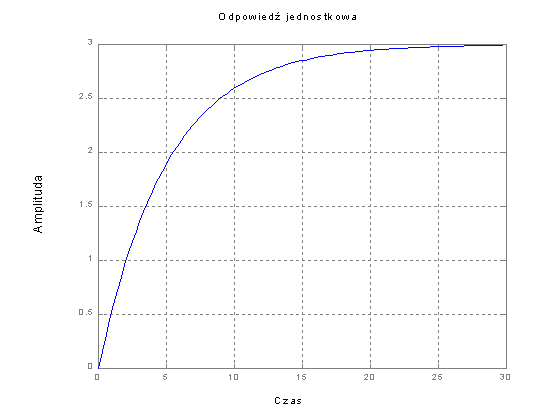
Rys. 1
Odpowiedź
jednostkowa układu wyznaczona poleceniem step(l,m)
Przykład 2
Dany jest
obwód elektryczny
jak na rys. 2. Należy wyznaczyć odpowiedź jednostkową układu w zakresie
czasu t
= 0 do 30. Przyjmiemy, że wymuszeniem jest funkcja jednostkowa u1 =
1(t),
przy napięciu u2 = 0.
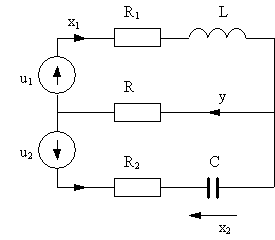
Rys. 2
Schemat obwodu
elektrycznego
Jako
współrzędne stanu
obieramy prąd x1 w gałęzi R1, L oraz napięcie x2
na kondensatorze C, zaś jako wyjście y, prąd w gałęzi R. Wielkościami
wejściowymi są napięcia u1 i u2.
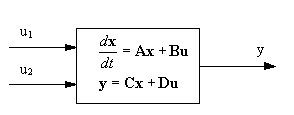
Na podstawie pierwszego i drugiego prawa
Kirchhoffa
otrzymujemy układ równań, który po przekształceniu do postaci (2)
przedstawia
się następująco:
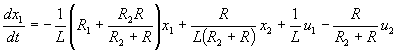
![]()
![]()
Stąd
mamy
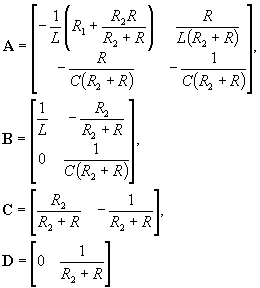
Użyjemy teraz
dla odmiany
polecenia [y,x]=step(A,B,C,D,IU,t)z
lewostronnymi argumentami y i x oraz prawostronnymi A,B,C,D,IU,t.
Argument IU oznacza numer wejścia, do którego przyłożono
funkcję skoku
jednostkowego.
Jeżeli
wykonanie zadania
wymaga użycia większej liczby poleceń, to wygodniej jest posłużyć się
tzw.
m-plikiem (ang. m-file). Do tego m- pliku tekstowego (rozszerzeniem
jego nazwy
musi być litera m), czyli skryptu zapisujemy następującą sekwencję
poleceń:
R1
=1; % parametr obwodu
elektrycznego
R2 =2; % jak wyżej
R =3; % jak wyżej
L =1e-4; % jak wyżej
C =1e-4; % jak wyżej
A=[-(R1+R2*R/(R2+R)),R/(L*(R2+R));
-R/(C*(R2+R)),-1/(C*(R2+R))]; % macierz stanu
B=[1/L,-R/(R2+R);0,1/(C*(R2+R))]; %
macierz wejścia
C=[R2/(R2+R),-1/(R2+R)];
%
macierz wyjścia
D=[0,1/(R2+R)];
%
macierz transmisji
t=0:1e-6:2e-3;
%
zadawanie wektora czasu
[y,x]= step(A,B,C,D,1,t);
%
obliczanie odpowiedzi
x1=x(:,1); % wybór pierwszej kolumny z
macierzy odpowiedzi x
x2=x(:,2); % analogicznie jak wyżej
wybór drugiej kolumny
plot(t,x1,t,x2,’c--’,t,y,’g:’); %
polecenie rysowania wykresu
axsis([0 30 -2 4]); % skalowanie osi
układu współrzędnych
grid on;
% nakładanie siatki
na układ współrzędnych
xlabel(‘Czas, sek’); % etykieta osi
czasu
ylabel(‘Odpowiedź’); % etykieta osi odpowiedzi
title(‘Odpowiedź jednostkowa’); % tytuł wykresu
gtext(‘x1’); % wprowadzanie tekstu w miejscu wskazanym myszką
gtext(‘x2’); % jak wyżej
gtext(‘y’);
% jak wyżej
Wykonanie
poleceń
zapisanych w skrypcie odbywa się przez wprowadzenie, w oknie poleceń
MATLAB-a,
jego nazwy bez rozszerzenia
Powyższy
przykład jest
ilustracją stosowania polecenia step do wyznaczania odpowiedzi
jednostkowej
układu dwuwymiarowego opisanego równaniami w przestrzeni stanów.
Pierwsze
cztery argumenty prawostronne tego polecenia są obliczane z zależności
wiążących macierze A, B, C, D z parametrami obwodu R1, R2,
R, L, C, piąty argument określa numer wejścia, w tym przypadku jest to
wejście
o numerze 1. Drugie wejście ma przyjętą domyślnie przez program wartość
zerową.
Wykonanie
wykresów za
pomocą polecenia plot pozwala na wybór rodzaju i atrybutów
poszczególnych linii. Wprowadzono ponadto szereg poleceń, które
pozwoliły
między innymi na dostosowanie rysunku do wymagań użytkownika, np. przez
nałożenie siatki na układ współrzędnych, dołączenie tytułu wykresu i
etykiet
osi (w języku polskim) itd.
Zwracamy
uwagę, że tekst
umieszczony za znakiem % jest komentarzem i przez program nie jest
wykonywany.
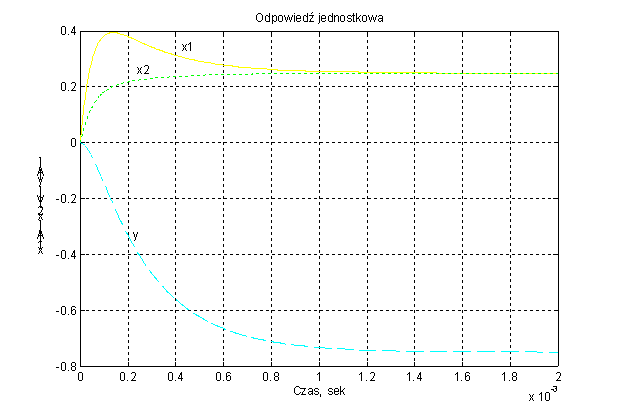
Rys. 2 Odpowiedź jednostkowa układu
opisanego równaniami stanu dla u1 = 1(t), u2 = 0
Odpowiedź
impulsową układu
uzyskuje się w analogiczny sposób jak
odpowiedź jednostkową a jedynie
polecenie step zastępujemy poleceniem impulse.
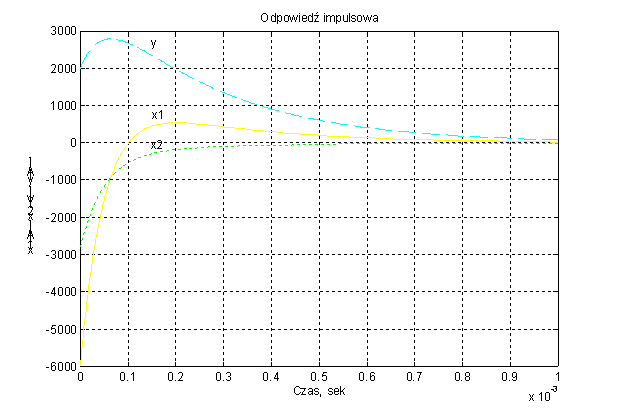
Rys. 3
Odpowiedź impulsowa układu dla u1 = 0, u2 = d(t)
Polecenia
służące do
tworzenia charakterystyk częstotliwościowych: nyquist, bode,
nichols,
margin.
Tabela 4. Polecenia
do tworzenia charakterystyk częstotliwościowych
|
Nazwa |
Opis polecenia |
|
nyquist |
wykonuje charakterystykę
Nyquista układu ciągłego |
|
bode |
wykonuje charakterystykę Bodego
układu ciągłego |
|
margin |
wyznacza margines amplitudy i
fazy na charakterystyce Bodego dla układu ciągłego |
|
nichols |
wykonuje charakterystykę
Nicholsa układu ciągłego |
|
covar |
kowariancja odpowiedzi układu
ciągłego na biały szum |
|
dnyquist |
wykonuje charakterystykę
Nyquista układu dyskretnego |
|
dbode |
wykonuje charakterystykę Bodego
układu dyskretnego |
|
dnichols |
wykonuje charakterystykę
Nicholsa układu dyskretnego |
|
imargin |
wyznacza margines amplitudy i
fazy przez interpolację |
|
Dcovar |
kowariancja odpowiedzi układu
dyskretnego na biały szum |
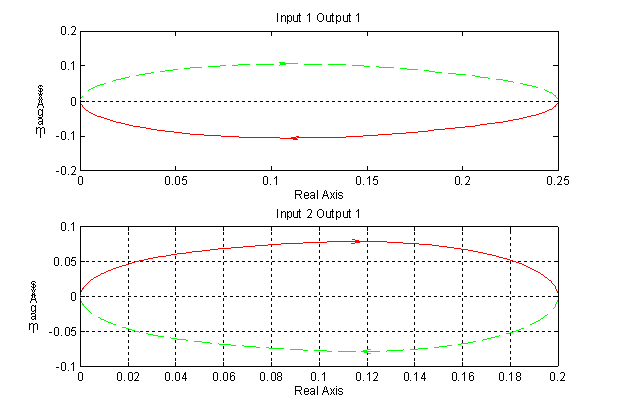
Rys. 4 Charakterystyki
Nyquista

Rys. 5 Charakterystyki bodego dla u1
= sin(wt) przy u2 = 0
Przykład 3
W układzie
jak na rys. 6
wyznaczyć przebiegi napięcia i prądu oraz określić wartość przepięcia na kondensatorze C2, jeżeli
sinusoidalne
napięcie wejściowe załączono bez łukowo z opóźnieniem to =
5msek.
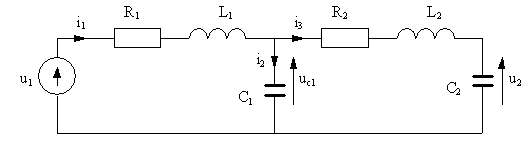
Rys.6 Schemat
obwodu
elektrycznego
Na podstawie
równań
Kirhchoffa mamy
![]()
![]()
![]()
Uwzględniając
związek
zachodzący pomiędzy prądem a napięciem na kondensatorze, możemy napisać
![]()
![]()
Stąd po
przekształceniu
otrzymujemy układ równań stanu
![]()
![]()
![]()
![]()
Do
rozwiązania powyższego
układu równań użyjemy teraz polecenia lsim według składni:
[y,x]=lsim(a,b,c,d,u,t)
R1=1;
R2=1.2;
C1=0.53e-6;
C2=1.06e-6;
L1=0.52e-3;
L2=1.04e-3;
%Um=sqrt(2/3)*15e3;
Um=30e3*sqrt(2);
freq=2*pi*50;
num=1;
den=[L1*L2*C1*C2
L1*C1*R2*C2+R1*C1*L2*C2;
R1*C1*R2*C2+C1*L1+L1*C2+C2*L2
R1*C2+R2*C2 1];
a=[-R1/L1,0,-1/L1,0;
0,-R2/L2,1/L2,-1/L2;
1/C1,-1/C1,0,0;
0,1/C2,0,0];
b=[1/L1;0;0;0];
c=[0,0,0,1];
d=[0];
ts=10e-3;
to=5e-3;
t=0:ts*1e-3:ts;
u=Um*sin(freq*t).*stepfun(t,to); %u=Um*stepfun(t,to);
[y,x]=lsim(a,b,c,d,u,t);
%[y,x]=lsim(num,den,u,t);
y=c*x';
x1=x(:,1);
x2=x(:,2);
x3=x(:,3);
x4=x(:,4);
ymin=min(y);
ymax=max(y);
t=t*1e3;
figure(1);plot(t,u',t,y);xlabel('t,msek');ylabel('U, V');
grid on;title('Napięcie we-wy');%axis([0 ts ymin ymax]);
figure(2);plot(t,x1);grid on;title('Prąd i1');
figure(3);plot(t,x2);grid on;
figure(4);plot(t,x3);grid on;
figure(5);plot(t,x4);grid on;
figure(6);
subplot(2,2,1);plot(t,u',t,y);xlabel('t, msek');
grid on;title('Napięcie we-wy');
subplot(2,2,2);plot(t,x1);grid on;title('Prąd i1');
subplot(2,2,3);plot(t,x2);grid on;
subplot(2,2,4);plot(t,x4);grid on;
save ga_dane.dat x –ascii
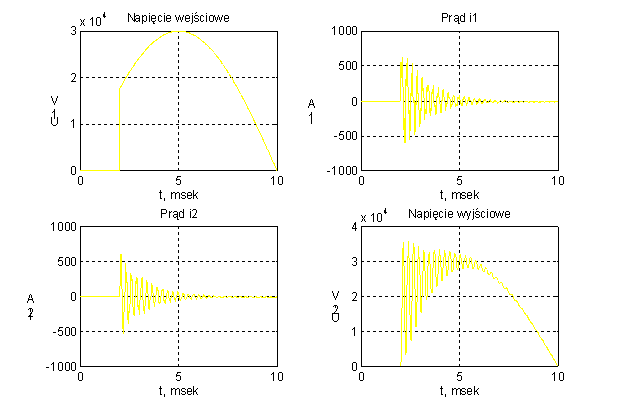
Rys. 7
Przebiegi napięć i prądów w układzie