1 Stabilność liniowych układów sterowania
Układ zamknięty liniowy i stacjonarny opisany równaniem (1) jest stabilny, jeżeli dla skończonej wartości zakłócenia przy dowolnych wartościach początkowych jego odpowiedź ustalona przyjmuje skończone wartości.
![]() (1)
(1)
Transmitancja operatorowa tego układu ma postać:
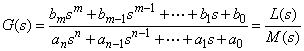 (2)
(2)
Stąd jego równanie charakterystyczne
![]() (3)
(3)
W ujęciu matematycznym warunkiem koniecznym i dostatecznym na to, ażeby układ zamknięty był stabilny jest, aby pierwiastki równania charakterystycznego (3) miały ujemne części rzeczywiste. Rozwiązanie tego równania wystarczy, więc dla stwierdzenia czy dany układ liniowy jest stabilny. Jednak w praktyce ta metoda nie zawsze jest dogodna i wystarczająca.
Z tego względu zostały opracowane metody pozwalające na badanie stabilności bez rozwiązywania równania charakterystycznego są to tzw. kryteria stabilności. Kryteria te dzielą się na: algebraiczne do, których należą kryteria Routha i Hurwitza oraz częstotliwościowe Michajłowa i Nyquista.
1.1 Kryterium Hurwitza
Warunkiem koniecznym i dostatecznym stabilności układu
liniowego i stacjonarnego jest, ażeby wszystkie współczynniki wielomianu
charakterystycznego transmitancji tego układu istniały i były dodatnie, a ponadto
ażeby wyznacznik ![]() (1) zwany
wyznacznikiem Hurwitza oraz jego podwyznaczniki
(1) zwany
wyznacznikiem Hurwitza oraz jego podwyznaczniki ![]() były dodatnie.
były dodatnie.
Jeżeli którykolwiek współczynnik jest ujemny lub równy zeru albo którykolwiek podwyznacznik jest ujemny to układ jest niestabilny.
Jeśli dowolny z podwyznaczników jest równy zeru to oznacza, że równanie charakterystyczne układu ma między innymi pierwiastki urojone i wtedy układ jest na granicy stabilności. Na jego wyjściu występują drgania o ustalonej amplitudzie.
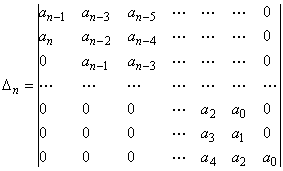 (4)
(4)
![]()
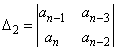
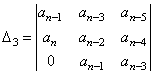
![]()
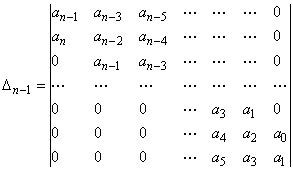
Przykład 1
Za pomocą kryterium Hurwitza zbadać stabilność układu zamkniętego, którego równanie charakterystyczne ma postać:
![]()
Zauważmy, że spełniony jest warunek konieczny stabilności, ponieważ wszystkie współczynniki równania charakterystycznego są dodatnie.
Wyznacznik Hurwitza utworzony ze współczynników wielomianu tego równania ma postać:
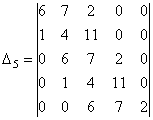
Obliczamy wartość wyznacznika za pomocą polecenia det, które wprowadzamy w oknie poleceń MATLAB-a według poniższej składni. Argumentem polecenia det zapisanym w nawiasach okrągłych jest macierz współczynników wyznacznika Hurwitza, która z kolei zapisana jest w nawiasach kwadratowych. Poszczególne elementy wierszy tej macierzy oddzielone są odstępami, natomiast wiersze – oddzielone są średnikami.
» delta_5=det([6 7
2 0 0;1 4 11 0 0;0 6 7 2 0;0 1 4 11 0;0 0 6 7 2]),
delta_5 =
-5846
Ujemna wartość wyznacznika Hurwitza wskazuje na to, że badany układ jest niestabilny.
1.2 Kryterium Nyquista
Kryterium Nyquista pozwala na badanie stabilności
jednowymiarowego układu zamkniętego na podstawie przebiegu wykresu funkcji ![]() układu otwartego na płaszczyźnie zmiennej zespolonej.
układu otwartego na płaszczyźnie zmiennej zespolonej.
Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:
a)
Jeżeli układ otwarty jest stabilny to układ zamknięty jest też
stabilny wtedy i tylko wtedy, gdy wykres charakterystyki ![]() przy wzroście
przy wzroście ![]() od 0 do
od 0 do ![]() , nie obejmuje punktu o współrzędnych (-1, j0).
, nie obejmuje punktu o współrzędnych (-1, j0).
b)
Jeżeli układ otwarty nie jest stabilny i jego transmitancja ma
r biegunów w prawej półpłaszczyźnie zmiennej zespolonej to układ zamknięty jest
stabilny wtedy i tylko wtedy, gdy wykres charakterystyki ![]() przy wzroście
przy wzroście ![]() od 0 do
od 0 do ![]() , obejmuje punkt (-1,j0) r/2 razy.
, obejmuje punkt (-1,j0) r/2 razy.
W pewnych przypadkach wygodniej jest posługiwać tzw. regułą
lewej strony, która mówi, że układ zamknięty jest stabilny, jeżeli przy
wzroście ![]() od 0 do
od 0 do ![]() , punkt (-1,j0) znajduje się w obszarze po lewej stronie
wykresu Go(jw).
, punkt (-1,j0) znajduje się w obszarze po lewej stronie
wykresu Go(jw).
W praktycznych zastosowaniach kryterium Nyquista jest
szczególnie przydatne w przypadku, gdy układ otwarty jest stabilny. Można wtedy
korzystać z przebiegu charakterystyki ![]() układu otwartego
zdjętej doświadczalnie, co pozwala na badanie stabilności także układu, którego
opis matematyczny nie jest znany.
układu otwartego
zdjętej doświadczalnie, co pozwala na badanie stabilności także układu, którego
opis matematyczny nie jest znany.
Przykład 2
Obiekt o transmitancji
![]()
pracuje w układzie zamkniętym z regulatorem proporcjonalno-całkującym o transmitancji
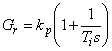
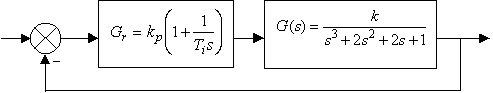
Rys. 1 Schemat układu zamkniętego z obiektem statycznym trzeciego rzędu i regulatorem PJ
Transmitancja układu otwartego
![]()
Rozpatrzymy dwa przypadki regulacji: z regulatorem nastawionym na działanie wyłącznie proporcjonalne i drugi – z regulatorem proporcjonalno-całkującym.
a) Przyjmiemy wzmocnienie obiektu
k = 1 oraz wyłączamy działanie całkujące regulatora przez nastawienie czasu
izodromu ![]() .
.
Stąd mamy
![]()
Za pomocą polecenia nyquist z pakietu MATLAB-a, wykonamy wykresy charakterystyk amplitudowo-fazowych układu otwartego Go(jw) dla trzech wartości wzmocnienia regulatora kp =2, 3 i 4.
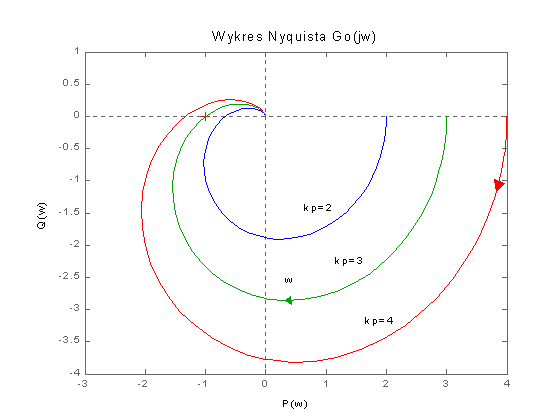
Rys. 2 Charakterystyki amplitudowo-fazowe układu otwartego Go(jw) dla kp = 2, 3, 4
Wykresy Nyquista układu otwartego Go(jw) obejmują trzy
charakterystyczne przypadki regulacji. W pierwszym z nich dla kp = 2
charakterystyka Go(jw) przy zwiększaniu częstotliwości ![]() nie obejmuje punktu
(-1,j0) – układ zamknięty jest wtedy stabilny. W drugim przypadku dla kp
= 3 charakterystyka G(jw) przechodzi przez punkt (-1,j0) – układ jest na granicy
stabilności. Wreszcie dla kp = 4 charakterystyka Go(jw) przy
wzroście
nie obejmuje punktu
(-1,j0) – układ zamknięty jest wtedy stabilny. W drugim przypadku dla kp
= 3 charakterystyka G(jw) przechodzi przez punkt (-1,j0) – układ jest na granicy
stabilności. Wreszcie dla kp = 4 charakterystyka Go(jw) przy
wzroście ![]() obejmuje punkt
(-1,j0) – układ po zamknięciu sprzężenia zwrotnego będzie niestabilny.
obejmuje punkt
(-1,j0) – układ po zamknięciu sprzężenia zwrotnego będzie niestabilny.
Potwierdzenie tego znajdujemy przez stwierdzenie położenia biegunów transmitancji układu zamkniętego na płaszczyźnie zmiennej zespolonej.
Wyznaczamy transmitancję układu zamkniętego
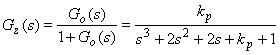
A stąd równanie charakterystyczne układu
![]()
Wyznaczamy pierwiastki równania charakterystycznego za pomocą polecenia roots z pakietu MATLAB-a, dla kp = 2 mamy
s1 = -1.8105
s2 = -0.0947 + 1.2837j
s3 = -0.0947 - 1.2837j
Jak widać wszystkie pierwiastki mają części rzeczywiste ujemne, czyli istotnie układ zamknięty spełnia warunek konieczny i dostateczny stabilności.
Obliczamy z kolei pierwiastki dla kp =3
s1 = - 2.0000
s2 = 0.0000 + 1.4142j
s3 = 0.0000 - 1.4142j
W tym przypadku występują pierwiastki urojone sprzężone, zatem układ zamknięty jest na granicy stabilności.
W końcu dla kp = 4, mamy pierwiastki
s1 = -2.1509
s2 = 0.0755 + 1.5228j
s3 = 0.0755 - 1.5228j
Tym razem występują pierwiastki zespolone sprzężone, których części rzeczywiste są dodatnie, wobec tego układ zamknięty jest dla tego przypadku niestabilny.
Innym sposobem jak najbardziej wizualnym, zaprezentowania reakcji układu zamkniętego na zakłócenie w postaci skoku jednostkowego przyłożonego do jego wejścia, jest przedstawienie przebiegów charakterystyk skokowych.
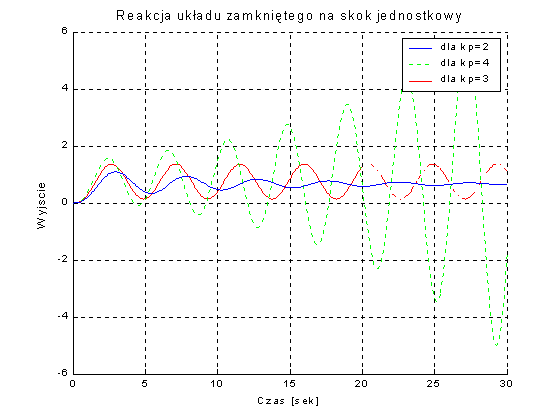
Rys. 3 Odpowiedzi układu zamkniętego z regulatorem proporcjonalnym na zakłócenie na wejściu w postaci skoku jednostkowego
b) Zbadamy teraz stabilność układu zamkniętego z regulatorem proporcjonalno-całkującym dla stałego wzmocnienia regulatora kp = 1 i różnych wartości czasu izodromu.
Wykonujemy charakterystyki amplitudowo-fazowe układu otwartego
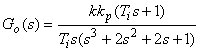
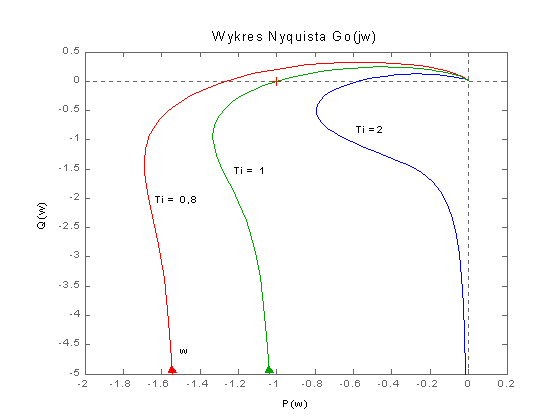
Rys. 4 Charakterystyki amplitudowo-fazowe układu otwartego Go(jw) z regulatorem proporcjonalno-całkującym przy kp = 1 dla czasu izodromu Ti = 0,8, 1 i 2
Układ otwarty jest w tym przypadku astatyczny ze względu na akcję całkującą regulatora. Charakterystyka Nyquista biegnie po ujemnych wartościach od minus nieskończoności do zera przy zwiększaniu częstotliwości od zera do nieskończoności. Kryterium stabilności może być w tym przypadku sformułowane następująco; układ zamknięty jest stabilny wtedy, gdy przy zwiększaniu częstotliwości od zera do nieskończoności, wykres Go(jw) omija punkt (-1,j0) po lewej stronie, a więc zgodnie z regułą lewej strony. W przeciwnym razie układ po zamknięciu będzie niestabilny. Jeżeli wykres Go(jw) przechodzi przez punkt (-1,j0), to układ zamknięty jest na granicy stabilności, a na jego wyjściu występują drgania o ustalonej amplitudzie, jak na wykresie dla Ti = 1 na rys. 5.
Transmitancja układu zamkniętego z regulatorem PI przyjmuje postać:
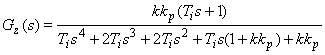
Stąd dla przyjętych wartości parametrów układu otrzymujemy przebiegi charakterystyk skokowych jak na rys. 5.
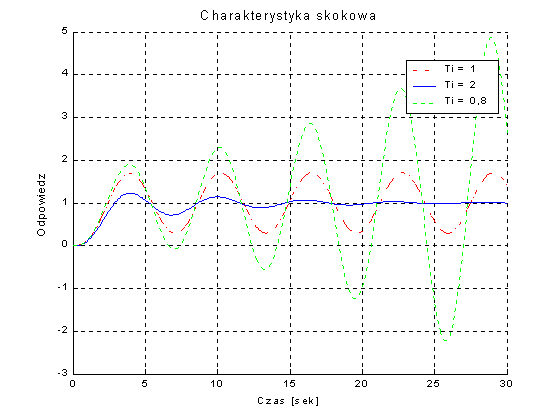
Rys. 5 Reakcja układu zamkniętego z regulatorem proporcjonalno-całkującym na zakłócenie na jego wejściu w postaci skoku jednostkowego
Zbadamy teraz położenie biegunów transmitancji układu zamkniętego z regulatorem proporcjonalno-całkującym. Posłużymy się tym razem poleceniem pzmap MATLAB-a, które tworzy wykres na płaszczyźnie zmiennej zespolonej z zaznaczonymi biegunami i zerami transmitancji układu zamkniętego. Jak widać na rys. 6 dla Ti = 0,8 dwa bieguny transmitancji mają części rzeczywiste dodatnie, więc układ zamknięty jest dla tej wartości czasu izodromu – niestabilny. Dla Ti = 1 układ ma dwa bieguny położone na osi urojonej, zatem jest na granicy stabilności. I wreszcie dla Ti = 2 wszystkie bieguny leżą w lewej półpłaszczyźnie, czyli układ jest w tym przypadku stabilny.
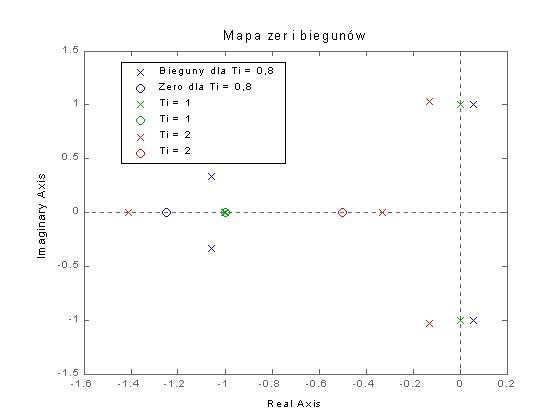
Rys. 6 Rozkład biegunów i zer transmitancji układu zamkniętego