Ćwiczenie 2
Charakterystyki częstotliwościowe obiektów
Program ćwiczenia
Wykonać charakterystyki amplitudowo-fazowe (Nyquista) oraz amplitudowe i fazowe logarytmiczne (Bodego) następujących obiektów:
- Inercyjny I – rzędu
![]()
- Całkujący z inercją
![]()
- Różniczkujący rzeczywisty
![]()
- Inercyjny II – rzędu
![]()
- Oscylacyjny II – rzędu
![]()
- Opóźniający z inercją
![]()
Tworzenie charakterystyk częstotliwościowych odbywa się za pomocą poleceń Matlab–a (Toolbox-u Control): nyquist i bode.
Stosowanie oraz składnię tych poleceń można znaleźć w pomocy Matlaba (np. help bode). Wykresy poszczególnych charakterystyk wykonanych dla trzech różnych kombinacji parametrów, należy zamieścić w osobnych oknach graficznych. Nakładanie wykresów w jednym układzie współrzędnych realizuje polecenie hold on (hold off – wyłącza nakładanie, hold – działa przełączająco).
W przypadku obiektu opóźniającego trzeba posłużyć się aproksymacją Padego, analogicznie jak w ćwiczeniu 1.
Sprawozdanie
W sprawozdaniu należy zamieścić wykonane charakterystyki. Wszystkie wykresy powinny być opisane i zinterpretowane w odpowiedni sposób np. dla obiektu inercyjnego I – rzędu trzeba określić wzmocnienie oraz stałą czasową. Ponadto należy podać dla każdego obiektu: równanie różniczkowe, transmitancję operatorową i widmową oraz napisać wzory określające charakterystyki Nyquista i Bodego.
Przykład 1
Wykonać charakterystykę amplitudowo – fazową obiektu opóźniającego z inercją:
![]()
dla k = 2,6, T = 8, To = 3, n = 5.
W oknie MATLAB Command Window wprowadzamy sekwencję następujących poleceń:
[lp,mp]=pade(3,5);
li=2.6;
mi=[8 1];
[lo,mo]=series(li,mi,lp,mp);
nyquist(lo,mo);
Pierwsze z tych poleceń służy do zdefiniowania aproksymacji Padego transmitancji operatorowej obiektu opóźniającego. Polecenia drugie i trzecie określają transmitancję członu inercyjnego I – rzędu. Z kolei polecenie series tworzy szeregowe połączenie członów: inercyjnego i opóźniającego. Ostatnie w ciągu poleceń nyquist, wykonuje charakterystykę amplitudowo – fazową.
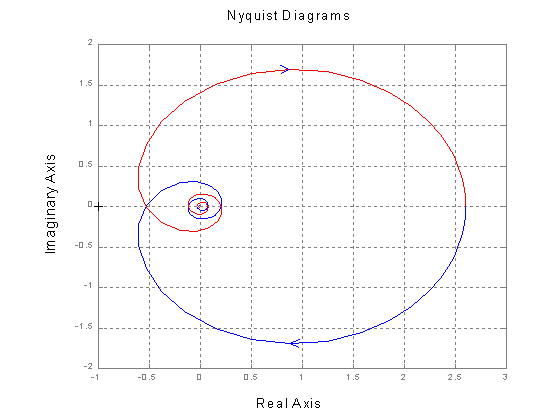
Rys. 2. Charakterystyka amplitudowo – fazowa (Nyquista) obiektu opóźniającego z inercją