Ćwiczenie 4

Charakterystyki czasowe i częstotliwościowe regulatorów

Program ćwiczenia

Wykonać charakterystyki czasowe (jednostkową i impulsową) oraz charakterystyki częstotliwościowe (Nyquista i Bodego) dla niżej podanych regulatorów:

1. Regulator proporcjonalny P

2. Regulator całkujący I

3. Regulator proporcjonalno-całkujący PI

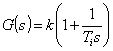
4. Regulator proporcjonalno-różniczkujący PD

5. Regulator proporcjonalno-różniczkujący PD rzeczywisty

6. Regulator proporcjonalno-całkująco-różniczkujący PID

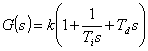
7. Regulator proporcjonalno-całkująco-różniczkujący PID rzeczywisty

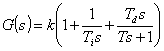
Utworzyć co najmniej po dwie charakterystyki dla każdego typu regulatora, przyjmując różne wartości parametrów.

Sprawozdanie

W sprawozdaniu należy zamieścić wykonane i opracowane charakterystyki. Podać równania różniczkowe, transmitancje operatorowe i widmowe a także wzory określające odpowiedzi czasowe (jednostkowe i impulsowe) oraz charakterystyki częstotliwościowe (Nyquista i logarytmiczne Bodego). Zaznaczyć i opisać charakterystyczne punkty na wykresach tych przebiegów.

Przykład 1

Wyznaczyć charakterystykę jednostkową regulatora proporcjonalno – różniczkującego PD rzeczywistego, którego transmitancja operatorowa ma postać:

dla k = 5, T_d = 2.4, T = 0.3

W oknie poleceń Matlaba-a wprowadzamy następujący ciąg poleceń:

k=5;Td=2.4;T=0.3;l=k*[Td+T 1];m=[T 1];step(l,m);

lub

k=5;Td=2.4;T=0.3;g=k*(1+tf([Td 0],[T 1])),step(g);

Druga postać jest wygodniejsza, ponieważ unikamy dodatkowych przekształceń transmitancji.

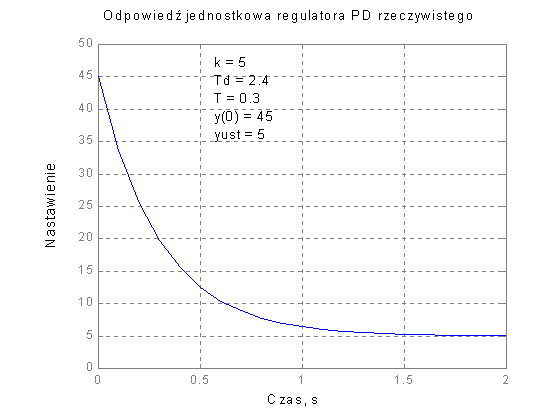
Rys. 1. Charakterystyka jednostkowa regulatora PD rzeczywistego (z inercją)

Przykład 2

Wyznaczyć charakterystykę Bodego regulatora proporcjonalno – różniczkującego PD rzeczywistego, którego transmitancja operatorowa ma postać:

dla k = 5, T_d = 2.4, T = 0.3

W oknie poleceń Matlaba-a wprowadzamy następujący ciąg poleceń:

k=5;Td=2.4;T=0.3;l=k*[Td+T 1];m=[T 1];bode(l,m);

lub

k=5;Td=2.4;T=0.3;g=k*(1+tf([Td 0],[T 1])),bode(g);

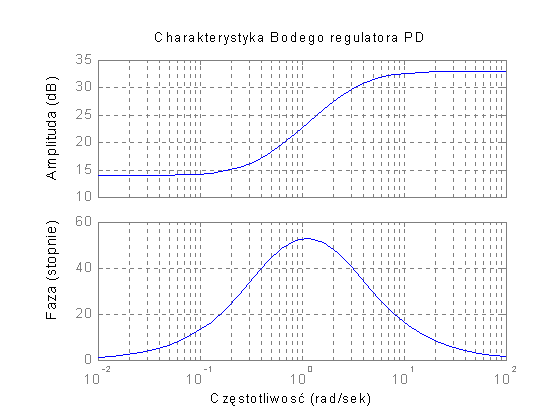
Rys. 2. Charakterystyki Bodego regulatora PD – z inercją

Przykład 3

Wyznaczyć charakterystykę czasową idealnego regulatora proporcjonalno-różniczkującego (PD). W tym przypadku należy się posłużyć wymuszeniem liniowym, wtedy odpowiedź regulatora ma czytelny charakter tzn. pokazuje działanie zarówno części proporcjonalnej jak i części różniczkującej.

Wykonanie charakterystyki realizuje następujący ciąg poleceń:

k=2;Td=0.8;t=0:.1:10;w=step(1,[1 0],t);y=step(k*[Td 1],[1 0],t);plot(t,w,t,y);

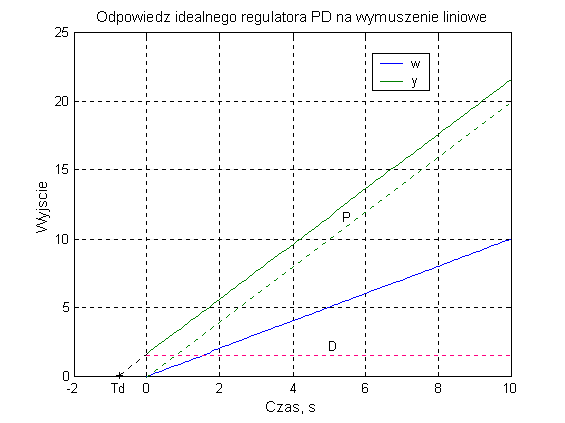
Rys. 3. Odpowiedź idealnego regulatora PD na wymuszenie liniowe

w – wymuszenie, y – wyjście regulatora, P – akcja proporcjonalna, D – akcja różniczkująca, Td – czas wyprzedzenia, k – wzmocnienie