]>
4.3.1 Example
4.3.1 Example
By applying, the formulae [22, 858.652, 861.16, 861.01] we can represent the Laplace transform of the
function
()
as
Now, (4.12), (4.13), (4.14), (4.16) yield the following results:
- For ,
(a real, negative
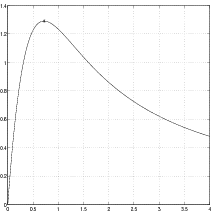
) the performance
index ,
is plotted at Figure 4.2 and it has a unique local (and thus global) maximum:
,
.
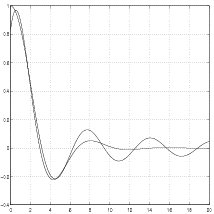
The corresponding approximating function takes the form
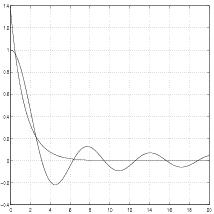
Its graph is compared with the graph of
at Figure 4.3.
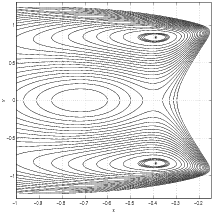
- For ,
(the real and
negative ,
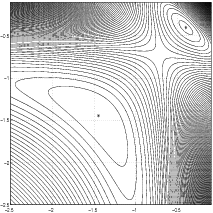
) the level curves of the
performance index ,
are depicted in Figure 4.4 and
has two local maxima: ,
,
,
(the global maximum). The corresponding approximating function takes the
form
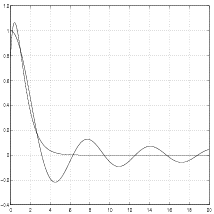
Its graph is compared with the graph of
at Figure 4.5.
- For ,
with additional
requirement ,
(clarify Remark 4.2.3) the level curves of the performance index
are depicted in Figure 4.6 and
has two global maxima: ,
.
The corresponding approximating function is real and takes the form
where
and .
Use the Laplace transform to confirm the last formula. Its graph is compared with the graph of
at Figure 4.7.
The above example shows that the numerical algorithms of global optimization should be applied to
solve the problem (4.12).
Exercise 4.3.1. Repeat the above calculations for the function
. Representing the
Laplace transform of
as
and applying formulae (4.12), (4.13), (4.14) we get:
- For ,
(a real negative )
has a local maximum (which is also global) ,
(compare with [52, p. 403]).
- For ,
(real and negative ,
)
has two local maxima such that ,
is the global maximum.
- For ,
with the requirement that
has two global maxima: ,
.