Table of Contents
Struktura kodu
Kod będziemy umieszczali w folderach o strukturze pozwalającej na zapis wszystkich projektów w repozytorium kodu ustalonym indywidualnie dla każdego uczestnika.
- Utwórz katalog root Może to być np.
programowanie-obiektowelub Twoje imię i nazwisko - Skopiuj tam do osobnego katalogu
Lab1pliki utworzone podczas pierwszych zajęć - Kod utworzony podczas kolejnych laboratoriów ma być umieszczany w katalogach
Lab2,Lab3, itd. - Czyli pliki utworzone podczas tych zajęć mają trafić do
Lab2
Laboratorium 2
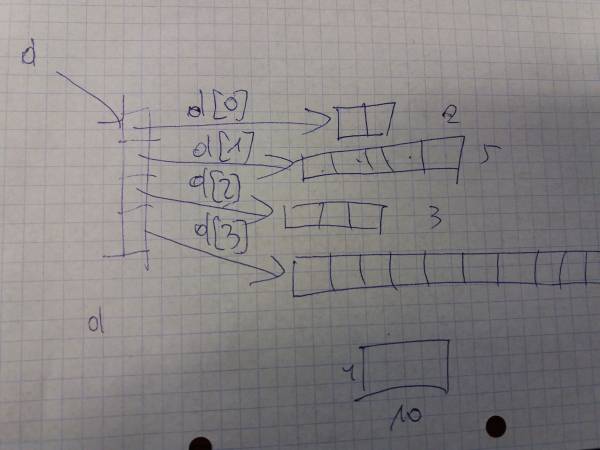
Klasa Matrix jest macierzą dwuwymiarową, ale dane przechowuje w tablicy jednowymiarowej data. Informacja o liczbie wierszy i kolumn jest zawarta w polach rows i cols
public class Matrix { double[]data; int rows; int cols; //... Matrix(int rows, int cols){ this.rows = rows; this.cols = cols; data = new double[rows*cols]; } //... }
Celem ćwiczenia jest implementacja różnych metod klasy Matrix oraz ich przetestowanie. Możesz wpierw wykonać punkt 2.11 i dodawać kod testujący na bieżąco…
2.1 Zaimplementuj konstruktor
Matrix(double[][] d){
tworzący macierz na podstawie tablicy - liczba kolumn ma być ustalona na podstawie najdłuższego wiersza w d, brakujace elementy zerowe.
Matrix m = new Matrix(new double[][]{{1,2,3,4},{5,6},{7,8},{9}});
2.2 Zaimplementuj metodę która zwraca tablicę dwuwymiarową
double[][] asArray()
2.3 Zaimplementuj metody dostępu do elementów (settery i gettery)
double get(int r,int c) void set (int r,int c, double value)
2.4 Zaimplementuj metodę toString
Publiczna funkcja toString powinna zwracać tekstową reprezentację obiektu. Klasa String jest niemodyfikowalna (immutable), dlatego do przygotowania tekstu użyj klasy StringBuilder. Obiekty tej klasy są modyfikowalne i bufor dla tekstu może automatycznie przyrastać w miarę dodawania kolejnych fragmentów. Przeciążona metoda append() pozwala na dopisywania tekstowej reprezentacji obiektów różnych typów (String, Object, double, float, int, itd.)
public String toString(){ StringBuilder buf = new StringBuilder(); buf.append("[") for(int i=0;i<rows;i++){ buf.append("["); //... } //... return buf.toString(); }
2.5 Zaimplementuj metodę reshape
void reshape(int newRows,int newCols){ if(rows*cols != newRows*newCols) throw new RuntimeException(String.format("%d x %d matrix can't be reshaped to %d x %d",rows,cols,newRows,newCols)); }
Na razie informuj o błędach za pomocą wyjątku RuntimeException. Jest to bardzo niewłaściwe i żaden programista Javy nigdy nie powinien tego robić. ![]() Ale niektórzy tak robią i zostaje w bibliotekach na długie lata.
Ale niektórzy tak robią i zostaje w bibliotekach na długie lata.
2.6 Zaimplementuj metodę shape
Metoda powinna zwracać tablicę określającą liczbę wierszy i kolumn
int[] shape()
2.7 Zaimplementuj metodę add
Matrix add(Matrix m)
Zwraca ona macierz, której elementy spełniają
assert( get(i,j) == this.get(i,j)+m.get(i,j) )
2.8 Analogicznie zaimplementuj metody
Matrix sub(Matrix m){...} Matrix mul(Matrix m){...} Matrix div(Matrix m){...}
oraz dodawanie, mnożenie, dzielenie, odejmowanie skalarów
Matrix add(double w){...} // dodaje wartość w do każdego elementu Matrix sub(double w){...} // odejmuje wartośc w od kazdego elementu Matrix mul(double w){...} // mnoży każdy element przez skalar w Matrix div(double w){...} // dzieli każdy element przez skalar w
2.9 Zaimplementuj zwykłe mnożenie macierzy.
W wyniku pomnożenia A(r x n) * B(n x m) ma powstać macierz C(r x m)
Matrix dot(Matrix m)
2.10 Zaimplementuj normę Frobeniusa
Norma Frobeniusa to po prostu suma kwadratów elementów. https://en.wikipedia.org/wiki/Matrix_norm#Frobenius_norm
double frobenius()
Czyli jeżeli odejmiemy macierz od siebie - to powinna powtać macierz o zerowej normie Frobeniusa. Jeśli podzielimy przez siebie - norma powinna wynosić rows * cols
2.11 Dodaj kod testujący
Uwaga ![]() To zadanie przeniesione na następne laboratorium
To zadanie przeniesione na następne laboratorium
Dla każdej z wcześniej podanych metod napisz kod testowy.
- Dodaj klasę
TestMatrix(w tym samym pakiecie) - Zaimplementuj kolejno statyczne metody o nazwie
testXXX, np:testMatrix()- test konstruktoratestAdd()- test dodawania- itd.
- Następnie wywołaj je w funkcji
main
2.12 Opcjonalnie: metody statyczne budujące macierze
Często spotykaną konwencją jest stosowanie metod statycznych, które tworzą skonfigurowany obiekt Zaimplementuj typowe metody:
public static Matrix random(int rows, int cols){ Matrix m = new Matrix(rows,cols); Random r = new Random(); m.set(0,0,r.nextDouble()); //... wypełnij wartościami losowymi return m; }
Wywołanie:
Matrix r = Matrix.random(2,3);
Macierz jednostkowa
public static Matrix eye(int n){ Matrix m = new Matrix(n,n); //... wypełnij jedynkami na przekątnej return m; }
2.13 Opcjonalnie: odwracanie macierzy
Jeżeli ktoś ma ochotę może napisać metodę inv() zwracającą odwrotność macierzy. Macierz może być odwrócona metodą eliminacji Gaussa.
Znalazłem gdzieś na dysku stary kod w C++ z 1995 roku. Może się przydać jako źródło inspiracji… Wydaje mi się, że działał?
- Konstruktor tworzył macierz jednostkową (z jedynkami na przekątnej)
- Pivot to element maksymalny w obszarze do eliminacji
- Nie chcemy wersji in place. Po prostu wynikowa macierz ma być zwracana
- Testy - pomnóż wektor przez macierz i następnie jej odwrotność i sprawdź, czy osiągnięto wartość wyjściową. Albo pomnóż macierz przez odwrotność i sprawdź, czy wynikowa macierz jest jednostkowa.
void Matrix::swapRows(int i1,int i2) { for(int j=0;j<n;j++){ double tmp=x[i1][j]; x[i1][j]=x[i2][j]; x[i2][j]=tmp; } } void Matrix::invert() { int i,j,k; Matrix out(n); for(i=0; i<n; i++){ // Find pivot row double max=fabs(x[i][i]); int pivot=i; for(k=i;k<n;k++){ if(max<fabs(x[k][i])){ max=fabs(x[k][i]); pivot=k; } } if(i!=pivot)swapRows(i,pivot); if(i!=pivot)out.swapRows(i,pivot); if(x[i][i] != 1.0){ double divby=x[i][i]; if( fabs(divby)>verySmall ){ for(j=0;j<n;j++){ out.x[i][j]/=divby; x[i][j]/=divby; } }else { throw -1; } } for(j=0;j<n;j++){ if(j!=i){ if(x[j][i]!=0){ double mulby=x[j][i]; for(k=0;k<n;k++){ x[j][k]-=mulby*x[i][k]; out.x[j][k]-=mulby*out.x[i][k]; } } } } } *this=out; }