MES w dynamice konstrukcji

Celem zastosowania metody elementów skończonych (MES) jest stworzenie modelu matematycznego systemu rzeczywistego (np. bryły poddanej rozciąganiu) poprzez rozwiązanie opisujących go równań różniczkowych cząstkowych poprzez ich zamianę na równania różniczkowe zwyczajne w procesie dyskretyzacji, uwzględnienie warunków początkowych i brzegowych. Obszar systemu dzielony jest na elementy na których krawędziach znajdują się węzły w których interpolowane są parametry opisujące układ (np. przemieszczenia węzłowe).

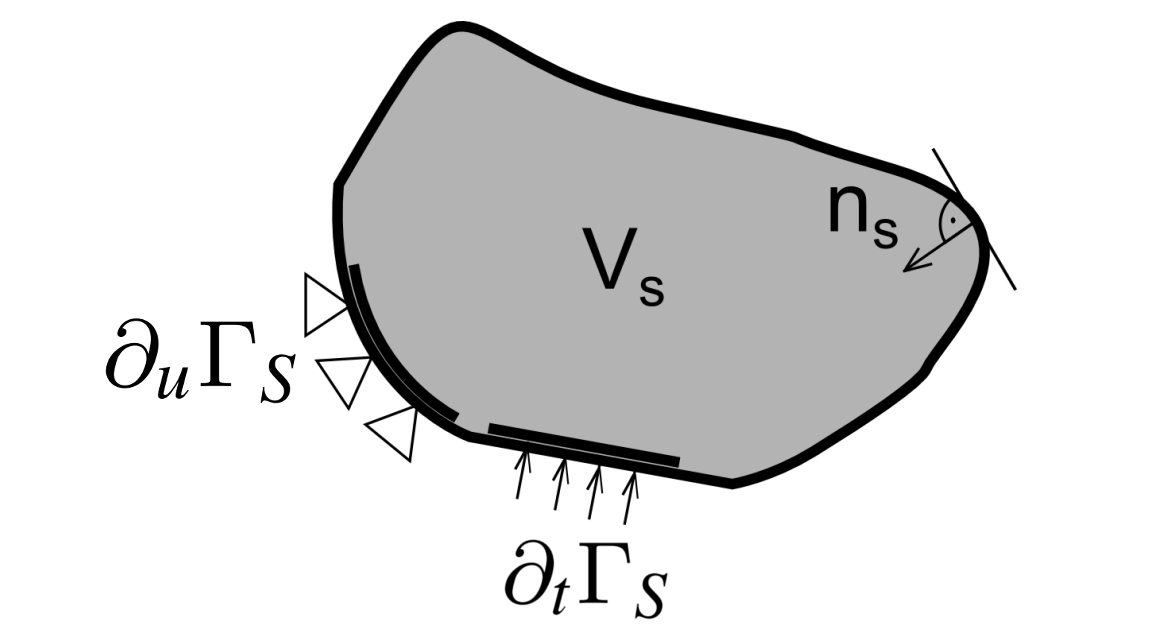
Na podstawie równań opisujących równowagę sił działających na konstrukcję oraz zasady zachowania pędu prawdziwa jest zależność:

(1)\[\rho\frac{\partial^{2}\vec{u}}{\partial t^{2}}+\mu\frac{\partial \vec{u}}{\partial t} -\nabla\cdot\bar{\bar{\sigma }}-\vec{b}_{i}=0\]

gdzie: \(\bar{\bar{\sigma }}\) to tensor naprężeń (Cauchy’ego), \(\vec b\) to wektor sił objętościowych, \(\vec u\) – wektor przemieszczeń, \(\rho\) –- gęstość, \(\mu\) -– współczynnik tłumienia. Równanie (1) można zapisać równoważnie jako

(2)\[\boxed{ \rho\frac{\partial^{2}u_{i}}{\partial t^{2}}+\mu\frac{\partial u_{i}}{\partial t}-\sigma_{ji,j}-b_{i}=0,\thinspace\thinspace\thinspace\thinspace i,j=1,2,3}\]

Warunki brzegowe można przyjąć jako warunek Neumanna poprzez definicję sił działających na brzeg \(\partial_t\Gamma_{S}\) lub Dirichleta poprzez zdefiniowanie wartości przemieszczeń na brzegu \(\partial_u\Gamma_{S}\)

(3)\[\begin{split}\begin{aligned} \left (\sigma_{ij} n_{j} \right){\vert_{\partial_t\Gamma_{S}}}=\bar{t_{i}} \\ \left(u_{i}\right){\vert_{\partial_u\Gamma_{S}}}=\bar{u}_{i}\end{aligned}\end{split}\]

Tensor naprężeń wyznacza się na podstawie zależności konstytutywnych. Jego składowe przyjmują wartości:

(4)\[\boxed{ \sigma_{ij}=D_{ijkl}\varepsilon_{kl} }\]

gdzie \(\varepsilon_{kl}\) to odkształcenia a \(D_{ijkl}\) to elementy macierzy konstytutywnej. Dla materiału izotropowego jego własności definiują dwa parametry: moduł Younga \(E\) i współczynnik Poissona \(\nu\). Prowadzi to do zależności

(5)\[D_{ijkl}=\frac{E}{2(1+\nu)}\left(\delta_{il} \delta_{jk}+\delta_{ik}\delta_{jl}\right)+\frac{E\nu}{(1+\nu)(1-2\nu)}\delta_{ij}\delta_{kl}\]

gdzie \(\delta_{ij}\) to symbol Kroneckera, czyli \(\delta_{ij}=0\) jeżeli \(i\neq j\) oraz \(\delta_{ij}=1\) jeżeli \(i=j\).

Odkształcenia zależą od przemieszczeń oraz wirtualne odkształcenia zależą od wirtualnych przemieszczeń zgodnie z zależnościami kinematycznymi (geometrycznymi)

(6)\[\boxed{ \varepsilon_{ij}=\frac{1}{2}\left(u_{i,j}+ u_{j,i}\right), ~~\delta\varepsilon_{ij}=\frac{1}{2}\left(\delta u_{i,j}+\delta u_{j,i}\right),\thinspace\thinspace\thinspace\thinspace i,j=1,2,3 }\]

Równanie (2) jest spełnione w całej objętości \(\Omega_{S}\). Po uwzględnieniu (3) równanie (2) zapisuje się w postaci całkowej jako

(7)\[\int\limits_{\Omega_{S}}\delta u_{i}\rho\frac{\partial^{2}u_{i}}{\partial t^{2}}d\Omega + \int\limits_{\Omega_{S}}\delta u_{i}\mu\frac{\partial u_{i}}{\partial t}d\Omega + \int\limits_{\Omega_{S}}\delta\varepsilon_{ij}\sigma_{ij}d\Omega - \int\limits_{\Omega_{S}}\delta u_{i}b_{i}d\Omega - \int\limits_{\Gamma_{S}}\delta u_{i}\bar{t_{i}}d\Gamma=0\]

W postaci macierzowej równanie (7) zapisuje się jako

(8)\[\int\limits_{\Omega_{S}}\delta \mathbf{u}^T\rho\mathbf{\ddot u}d\Omega + \int\limits_{\Omega_{S}}\delta \mathbf{u}^T\mu\mathbf{\dot u}d\Omega + \int\limits_{\Omega_{S}}\delta \mathbf{\varepsilon}^T\mathbf{\sigma}d\Omega - \int\limits_{\Omega_{S}}\delta\mathbf{u}^T\mathbf{b}d\Omega - \int\limits_{\Gamma_{S}}\delta\mathbf{u}^T \mathbf{\bar t}d\Gamma=0\]

Przyjmując wektor współrzędnych kartezjańskich \(\mathbf{x}=[x_1 ~ x_2 ~x_3]^T\) wektor przemieszczeń w \(n\) węzłach elementu skończonego ma postać \(\mathbf{u_e}=\left[ u_{11} ~ u_{21} ~ u_{31} ~ u_{12} ~ u_{22} ~ u_{32} ~ u_{13} ~ u_{23} ~ u_{33} ~ ... ~ u_{1n} ~ u_{2n} ~ u_{3n}\right]^T\).

Aproksymację przemieszczeń węzłowych oraz wirtualnych przemieszczeń w kierunku \(\mathbf{x}\) i czasie \(t\) zapisuje się jako

(9)\[\mathbf{u}(\mathbf{x},t)=\mathbf{N}(\mathbf{x})\mathbf{u}_e(t),~~\delta\mathbf{u}(\mathbf{x})=\mathbf{N}(\mathbf{x})\delta\mathbf{u}_e(t)\]

\(\mathbf{N}(\mathbf{x})\) to macierz funkcji kształtu \(N_1, N_2, N_3\) z których każda w węźle którego dotyczy przyjmuje wartość \(1\), a w pozostałych węzłach przyjmuje wartość \(0\) i zapisuje się ją jako

\(\left[ N_{1} ~ 0 ~ 0 ~ N_{2} ~ 0 ~ 0 ~ N_{3} ~ 0 ~ 0 ~.. ~ N_{n} ~ 0 ~ 0 ;~0 ~N_{1} ~ 0 ~ 0 ~ N_{2} ~ 0 ~ 0 ~ N_{3} ~ 0 ~.. ~ 0 ~ N_{n} ~ 0 ;~0~ 0 ~N_{1} ~ 0 ~ 0 ~ N_{2} ~ 0 ~ 0 ~ N_{3} ~ .. ~ 0 ~ 0 ~ N_{n} \right]\)

Wyznaczenie odkształceń \(\mathbf{\varepsilon}\) oraz wirtualnych odkształceń \(\delta\mathbf{\varepsilon}\) na podstawie zależności

(10)\[\mathbf{\varepsilon}=\mathbf{B}\mathbf{u}_e, ~~\delta\mathbf{\varepsilon}=\mathbf{B}\delta\mathbf{u}_e\]

Macierz łącząca przemieszczenia z odkształceniami ma postać

\[\begin{split}\mathbf{B}=\left[\begin{array}{ccccccc} \mathbf{N}_{1,1} & 0&0 & \cdots & \mathbf{N}_{n,1} & 0&0\\ 0& \mathbf{N}_{1,2}&0 & \cdots &0& \mathbf{N}_{n,2}&0\\ 0&0 & \mathbf{N}_{1,3} & \cdots & 0&0 & \mathbf{N}_{n,3}\\ \mathbf{N}_{1,2} & \mathbf{N}_{1,1}& 0 & \cdots& \mathbf{N}_{n,2} & \mathbf{N}_{n,1}& 0\\ 0& \mathbf{N}_{1,3} & \mathbf{N}_{1,2} & \cdots& 0& \mathbf{N}_{n,3} & \mathbf{N}_{n,2}\\ \mathbf{N}_{1,3} & 0 & \mathbf{N}_{1,1} & \cdots& \mathbf{N}_{n,3} & 0 & \mathbf{N}_{n,1} \end{array}\right]\end{split}\]

Otrzymany wektor odkształceń zawiera sześć elementów \(\mathbf{\varepsilon} = [\varepsilon_{11}~\varepsilon_{22} ~\varepsilon_{33}~\gamma_{12}~\gamma_{23}~\gamma_{31}]^T\). Wyznaczenie wektora naprężeń o postaci \(\mathbf{\sigma} = [\sigma_{11}~\sigma_{22} ~\sigma_{33}~\sigma_{12}~\sigma_{23}~\sigma_{31}]^T\) przebiega na podstawie zależności konstytutywnych

(11)\[\mathbf{\sigma}=\mathbf{D}\mathbf{\varepsilon}\]

gdzie \(\mathbf{D}\) to macierz konstytutywna.

Wprowadzając notację

\[ \begin{align}\begin{aligned}\sigma_{11}=\sigma_1, \sigma_{22}=\sigma_2, \sigma_{33}=\sigma_3, \sigma_{23}=\sigma_4, \sigma_{31}=\sigma_5, \sigma_{12}=\sigma_6,\\\varepsilon_{11}=\varepsilon_1, \varepsilon_{22}=\varepsilon_2, \varepsilon_{33}=\varepsilon_3, 2\gamma_{23}=\varepsilon_4, 2\gamma_{31}=\varepsilon_5, 2\gamma_{12}=\varepsilon_6\end{aligned}\end{align} \]

równanie (11) zapisywane jest analogicznie do (4) jako

(12)\[\begin{split}\left[\begin{matrix}\sigma_1\\ \sigma_2\\ \sigma_3\\ \sigma_4\\ \sigma_5\\ \sigma_6\end{matrix}\right] = \left[\begin{matrix}\frac{1}{E} & \frac{-\nu}{E} & \frac{-\nu}{E} & 0 & 0 & 0\\ & \frac{1}{E} & \frac{-\nu}{E} & 0 & 0 & 0\\ & & \frac{1}{E} & 0 & 0 & 0\\ & & & \frac{2(1+\nu)}{E} & 0 & 0\\ &Sym& & &\frac{2(1+\nu)}{E} & 0\\ & & & & & \frac{2(1+\nu)}{E} \end{matrix}\right]^{-1} \left[\begin{matrix}\varepsilon_1\\ \varepsilon_2\\ \varepsilon_3\\ \varepsilon_4\\ \varepsilon_5\\ \varepsilon_6\end{matrix}\right]\end{split}\]

Można je także wyrazić przy pomocy stałych Lame’go:

\[\begin{split}\left[\begin{matrix}\sigma_1\\ \sigma_2\\ \sigma_3\\ \sigma_4\\ \sigma_5\\ \sigma_6\end{matrix}\right] = \left[\begin{matrix}\lambda+2\mu & \lambda & \lambda & 0 & 0 & 0\\ & \lambda+2\mu & \lambda & 0 & 0 & 0\\ & & \lambda+2\mu & 0 & 0 & 0\\ & & & \mu & 0 & 0\\ &Sym& & &\mu & 0\\ & & & & & \mu \end{matrix}\right] \left[\begin{matrix}\varepsilon_1\\ \varepsilon_2\\ \varepsilon_3\\ \varepsilon_4\\ \varepsilon_5\\ \varepsilon_6\end{matrix}\right]\end{split}\]

gdzie: \(\lambda=\frac{E\nu}{(1+\nu)(1-2\nu)}\) oraz \(\mu=G=\frac{E}{2(1+\nu)}\)

Równanie po uwzględnieniu (9) - (11)) zapisuje się w postaci zdyskretyzowanej jako

(13)\[\int\limits_{\Omega_{S}} \mathbf{N}^T\rho\mathbf{N}d\Omega \mathbf{\ddot{u}}_e +\int\limits_{\Omega_{S}} \mathbf{N}^T\mu\mathbf{N}d\Omega \mathbf{\dot{u}}_e +\int\limits_{\Omega_{S}}\mathbf{B}^T\mathbf{D}\mathbf{B}d\Omega \mathbf{u}_e -\int\limits_{\Omega_{S}} \mathbf{N}^T \mathbf{b}d\Omega -\int\limits_{\Gamma_{S}} \mathbf{N}^T \mathbf{\bar {t}}d\Gamma = 0\]

Upraszczając zapis uzyskiwane jest równanie różniczkowe zwyczajne

(14)\[\boxed{ \mathbf{M}_{S} \mathbf{\ddot{u}}_e+\mathbf{C}_{S}\mathbf{\dot{u}}_e+\mathbf{K}_{S}\mathbf{u}_e=\mathbf{f}_{S} }\]

gdzie \(\mathbf{M}_S, \mathbf{C}_S, \mathbf{K}_S\) to odpowiednio macierze bezwładności,tłumienia i sztywności konstrukcji, \(\mathbf{\ddot u}_e\), \(\mathbf{\dot u}_e\), \(\mathbf{u}_e\) - przyspieszenia, prędkości i przemieszczenia konstrukcji, \(\mathbf{f}_S\) - siły uogólnione. Wyrażone są one zależnościami

\[\mathbf{M}_{S} =\int\limits_{\Omega_{S}} \mathbf{N}^T\rho\mathbf{N}d\Omega ~,~~ \mathbf{C}_{S} =\int\limits_{\Omega_{S}} \mathbf{N}^T\mu\mathbf{N}d\Omega ~,~~ \mathbf{K}_{S} = \int\limits_{\Omega_{S}}\mathbf{B}^T\mathbf{D}\mathbf{B}d\Omega\]

\[\mathbf{f}_S = \int\limits_{\Omega_{S}}\mathbf{N}^T\mathbf{b}d\Omega + \int\limits_{\Gamma_{S}}\mathbf{N}^T \mathbf{\bar t}d\Gamma\]

Odpowiedź układu na wymuszenie harmoniczne o postaci \(\mathbf{f}_S=Re(\mathbf{\tilde{f}}_S e^{j \mathbf{\omega} t} )\) o częstości drgań \({\omega}\) i zespolonej amplitudzie \(\mathbf{\tilde f}_S\) opisuje równanie

(15)\[\boxed{ \left(-{\omega}^2 \mathbf{M}_S+j\omega\mathbf{C}_S+\mathbf{K}_S \right) \mathbf{\tilde u}_e=\mathbf{\tilde f}_S }\]

Poszukując częstotliwości drgań własnych układu rozwiązywane jest zagadnienie z pominięciem siły wymuszającej i tłumienia, przy założeniu przemieszczeń zmieniających się harmonicznie \(\mathbf{u}_e=Re\left(\mathbf{\tilde{u}}_e e^{j \mathbf{\omega} t} \right)\) o częstości drgań \({\omega}\) i zespolonej amplitudzie \(\mathbf{\tilde u}_e\). Przyjęte założenia pozwalają przekształcić równanie (14) do postaci

(16)\[\boxed{ \left(-{\omega}^2 \mathbf{M}_S+\mathbf{K}_S \right) \mathbf{\tilde u}_e=0 }\]

Następnie poprzez zastosowanie odpowiedniego algorytmu numerycznego (jak na przykład Lanczosa) można wyznaczyć wartości własne tego równania odpowiadające częstościom drgań własnych oraz wektory własne odpowiadające postaciom drgań własnych.