Graf 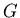 rzędu
rzędu 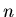 nazywamy pancyklicznym, jeśli dla każdej liczby naturalnej
nazywamy pancyklicznym, jeśli dla każdej liczby naturalnej 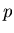 , , 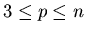 , , 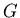 zawiera cykl długości
zawiera cykl długości 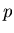 .
W 1971 roku Bondy postawił następującą "metahipotezę": prawie każdy warunek
wystarczający na to, aby graf był hamiltonowski implikuje również, że graf
ten jest pancykliczny, z wyjątkiem być może prostej rodziny grafów wyjątkowych.
W referacie przedstawimy szereg klasycznych już wyników związanych z powyższą
"metahipotezą" oraz podamy nowe twierdzenia o strukturze zbioru długości
cykli w grafie hamiltonowskim z małą liczbą wierzchołków wysokich stopni. .
W 1971 roku Bondy postawił następującą "metahipotezę": prawie każdy warunek
wystarczający na to, aby graf był hamiltonowski implikuje również, że graf
ten jest pancykliczny, z wyjątkiem być może prostej rodziny grafów wyjątkowych.
W referacie przedstawimy szereg klasycznych już wyników związanych z powyższą
"metahipotezą" oraz podamy nowe twierdzenia o strukturze zbioru długości
cykli w grafie hamiltonowskim z małą liczbą wierzchołków wysokich stopni. |
|
 Antoni MARCZYK
Antoni MARCZYK
Antoni MARCZYK