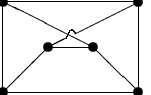
Niech 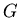 będzie grafem, który nie ma składowej będzie grafem, który nie ma składowej 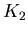 i ma co najwyzej
jedną składową i ma co najwyzej
jedną składową  . Jezeli krawedzie grafu . Jezeli krawedzie grafu 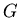 sa pokolorowane,
to zbiór kolorów
krawedzi incydentnych z wierzcho sa pokolorowane,
to zbiór kolorów
krawedzi incydentnych z wierzcho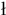 kiem kiem 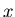 nazywamy
paletą wierzcho nazywamy
paletą wierzcho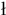 ka ka 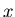 . Kolorowanie krawedzi grafu . Kolorowanie krawedzi grafu
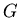 rozróznia jego wierzcho rozróznia jego wierzcho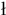 ki, jezeli rózne
wierzcho ki, jezeli rózne
wierzcho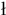 ki maja rózne palety. Indeks chromatyczny
rozrózniajacy wierzcho ki maja rózne palety. Indeks chromatyczny
rozrózniajacy wierzcho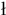 ki grafu ki grafu 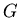 , , 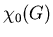 , jest najmniejszą
liczbą kolorów w kolorowaniu krawedzi , jest najmniejszą
liczbą kolorów w kolorowaniu krawedzi  rozrózniajacym
jego wierzcho rozrózniajacym
jego wierzcho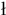 ki. ki.
Dla grafów 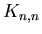 wiadomo (Zagaglia Salvi), ze
ciag wiadomo (Zagaglia Salvi), ze
ciag
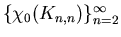 jest niemalejacy i zawiera
wszystkie liczby ca jest niemalejacy i zawiera
wszystkie liczby ca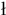 kowite kowite 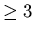 . Dla . Dla 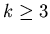 definiujemy liczbę definiujemy liczbę 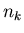 jako najwieksze jako najwieksze
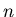 takie, ze takie, ze
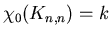 . Liczby . Liczby 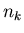 sa znane tylko dla sa znane tylko dla
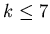 : : 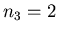 , , 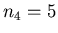 , , 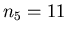 , ,  i i 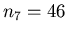 . Nietrudno wykazac,
ze . Nietrudno wykazac,
ze 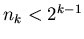 i i
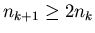 . Z tego wynika, że . Z tego wynika, że
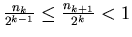 . A zatem granica . A zatem granica
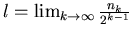 istnieje i istnieje i
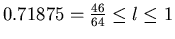 . Przedmiotem referatu bedzie szkic dowodu,
ze . Przedmiotem referatu bedzie szkic dowodu,
ze
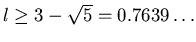 . .
Hipoteza (Hornák i Soták). 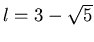 . .
Problem. Udowodnic przynajmniej, ze 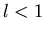 . .
|