Pudełko 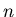 -wymiarowe to po prostu zbiór postaci -wymiarowe to po prostu zbiór postaci
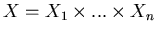 , gdzie , gdzie 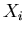 są pewnymi zbiorami skończonymi. Pudełeczkiem zawartym w są pewnymi zbiorami skończonymi. Pudełeczkiem zawartym w 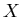 nazywamy pudełko nazywamy pudełko
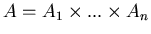 , ,
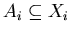 , spełniają ce
warunek , spełniają ce
warunek
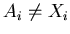 , dla wszystkich , dla wszystkich 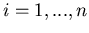 . Czy najmniejszą
liczbą pudełeczek, na które można podzielić . Czy najmniejszą
liczbą pudełeczek, na które można podzielić 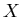 jest jest 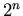 ?
To pytanie zostało postawione przez Kearnesa i Kissa (Finite
algebras of finite complexity, Discrete Math. 207 (1999), 89-135)
przy okazji badania tak zwanych algebr prostokątnych. A że
odpowiedź na nie jest pozytywna udowodnili niedawno Alon, Bohman,
Holzman i Kleitman (On partitions of discrete boxes, manuskrypt,
2001). Ich prosty i zarazem elegancki dowód opiera się na klasycznej
dwoistości ,parzyste-nieparzyste''.
Mimo szybkiego rozwiązania, problem Kearnesa i Kissa zdążył
pobudzić do rozmaitych uogólnień i dalszych dociekań. Oto
dwie, być może nietrudne kwestie, które pojawiły się
podczas kontemplacji pudeł , pudełek i pudełeczek. ?
To pytanie zostało postawione przez Kearnesa i Kissa (Finite
algebras of finite complexity, Discrete Math. 207 (1999), 89-135)
przy okazji badania tak zwanych algebr prostokątnych. A że
odpowiedź na nie jest pozytywna udowodnili niedawno Alon, Bohman,
Holzman i Kleitman (On partitions of discrete boxes, manuskrypt,
2001). Ich prosty i zarazem elegancki dowód opiera się na klasycznej
dwoistości ,parzyste-nieparzyste''.
Mimo szybkiego rozwiązania, problem Kearnesa i Kissa zdążył
pobudzić do rozmaitych uogólnień i dalszych dociekań. Oto
dwie, być może nietrudne kwestie, które pojawiły się
podczas kontemplacji pudeł , pudełek i pudełeczek.
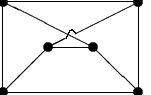
1. (Wersja grafowa) Niech 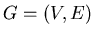 będzie grafem o średnicy będzie grafem o średnicy 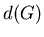 . Podzbiór . Podzbiór 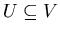 nazywamy wypukłym jeśli dla dowolnych nazywamy wypukłym jeśli dla dowolnych 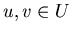 każda najkrótsza ścieżka łącząca każda najkrótsza ścieżka łącząca
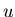 z z 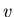 zawiera się w zbiorze zawiera się w zbiorze 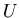 . Kolorowanie wierzchołków grafu . Kolorowanie wierzchołków grafu 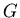 nazywamy antypodalnym, jeżeli klasy kolorów są wypukłe i dla każdej klasy nazywamy antypodalnym, jeżeli klasy kolorów są wypukłe i dla każdej klasy 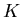 istnieje wierzchołek istnieje wierzchołek 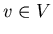 leżący w odległości leżący w odległości 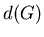 od od 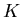 . Wreszcie, niech . Wreszcie, niech
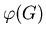 oznacza najmniejszą liczbę kolorów w antypodalnym
kolorowaniu grafu oznacza najmniejszą liczbę kolorów w antypodalnym
kolorowaniu grafu 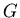 , lub , lub 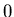 , jeśli takie kolorowanie nie istnieje.
Czy jest prawdą , że , jeśli takie kolorowanie nie istnieje.
Czy jest prawdą , że
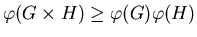 , dla dowolnych grafów , dla dowolnych grafów 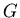 i i 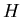 ? ?
2. (Wersja nieskończona) Czy pudełko 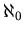 -wymiarowe
można podzielić na mniej niż -wymiarowe
można podzielić na mniej niż
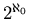 pudełeczek? pudełeczek?
|
|