Anna RYCERZ
                        (Wydzia³ Matematyki Stosowanej AGH)

Macierze doskona³e i grafy doskona³e



W $1972$ roku L.Lovász wykaza\l, ze graf $G$ jest doskona³y wtedy i tylko wtedy, gdy nastepujacy uk³ad nierówno¶ci

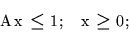
\begin{displaymath}Ax\leq 1,\ \ x\geq 0,\end{displaymath}

gdzie $A$ jest $0,1$ macierza incydencji klik w grafie $G$, jest totalnie dualnie ca³kowity (TDI). Macierz majaca te w³asnosc nazwano macierza doskona³a. W 1998 roku B.Guenin sformu³owa³ i udowodni³ analogiczne twierdzenie charakteryzujace bigrafy bidoskona³e.
Serdecznie zapraszamy wszystkich chêtnych !